高速铁路车站列车进路分配计算方法研究

林 枫

（中国铁道科学研究院集团有限公司运输及经济研究所，北京100081）

0 引言

随着我国经济社会的持续高速发展,城市规模及人口不断扩大,一些主要繁忙干线的运输能力越来越难以满足日益增长的旅客运输需求。高速铁路车站能力提升是点线能力协调优化的重要研究内容,车站主要由咽喉区和到发线组成,由于我国高速铁路车站咽喉区结构复杂,进路交叉干扰情况较多,研究车站能力提升首先根据道岔结构梳理咽喉区合理径路,更重要是明确到发线和咽喉区的相互关联关系,从而建立高速铁路车站列车进路分配模型。史峰等[1]建立起咽喉区的有向网络对进路进行优化研究；刘澜等[2]、吕颖等[3]、王宝山等[4]只针对到发线或咽喉区内作业合理性进行研究,并未对咽喉区和到发线相互制约关系进行统筹考虑；马驷等[5]结合咽喉区和到发线的关联关系进行研究,并建立咽喉区和到发线一体化的列车进路分配双层规划模型。

以高速铁路车站能力最大为目标进行列车进路分配,区别于给定列车时刻表的列车进路分配,前者是充分利用平行进路安排列车从而实现接发列车能力最大,而后者是以均衡利用到发线为目标。因而两者研究目标和方法不同。因此,主要针对以高速铁路车站能力最大为研究目标,充分利用平行进路来进行列车进路分配研究。

1 高速铁路车站列车进路分配双层规划模型构建

1.1 进路组成和分配影响因素分析

（1）组成分析。高速铁路车站列车进路是指列车在车站到、发、通过、折返、动车出入段过程中占用的车站内部一段线路。列车进路包括咽喉区径路和到发线,其中到发线是办理旅客列车到、发作业的线路,同一时刻每条到发线只能办理1项车站作业,在同一到发线的相邻2列车的车站作业过程需满足最小间隔时间。

咽喉区径路是指从车站(场)两端最外方道岔基本轨始端(或警冲标)至最内方出站信号机(或警冲标)的距离[5]。咽喉区径路由若干道岔组成,道岔按照不同用途和类型分组后,不同作业方式由不同道岔组合作完成。在办理车站各项作业时,如果咽喉区内某几条径路存在共用道岔组,则这几条径路相互干扰,不可同时被车站作业过程占用；反之,如果径路之间不存在共有道岔组,则可以同时被占用。从而梳理出咽喉区所有径路之间的关系。

咽喉区径路和到发线之间相互关联和制约,当咽喉区径路确定后,到发线也随之确定；而到发线确定后,可选择的咽喉区径路不止一条。

（2）影响因素分析。高速铁路车站列车进路分配时,主要影响因素有咽喉区径路冲突、车站作业时间约束和联络线设置等,其中咽喉区径路冲突是指折返列车作业时需要切割咽喉,从而存在到、发作业径路冲突,进而影响咽喉区能力利用；车站作业时间约束是指受信号开放时间和运输组织因素制约,不同列车作业之间存在最小间隔时间约束,从而保证车站各项作业安全；增设联络线可增加咽喉区平行径路,从而提高咽喉区作业效率。由于联络线设置属于车站设施设备改造措施,这里不予考虑。

高速铁路车站列车进路分配影响因素主要与列车种类有关,列车按作业方式主要分为始发列车、终到列车、通过列车和折返列车(这里指本线折返列车),其中通过列车又分为停站通过列车和不停站通过列车；车站作业过程主要与列车种类有关,分为出段作业、接车作业、发车作业、入段作业,到发作业(包括机车换挂、行邮装载、上水、旅客上车、乘检试风)[6]。高速铁路车站不同列车种类与列车作业过程关系如表1所示。

表1 高速铁路车站不同列车种类与列车作业过程关系Tab.1 Relation between different train types and train operation process in high-speed railway station

不同列车不同作业过程之间的最小间隔时间主要由车站设施设备配置情况决定,因而有小幅差别。

1.2 模型构建

在高速铁路车站列车进路分配时,如果已知列车到发车站时间,主要以列车站内走行时间之和最小[7-9]、到发线均衡使用为优化目标；但是以车站能力最大为目标进行列车进路分配时,需要在某一时间域内尽可能多地接发列车,因而考虑以具有平行作业关系的到发线的利用率最大为优化目标建立双层规划模型。

1.2.1 到发线与咽喉区径路关系分析

为建立高速铁路车站到发线和咽喉区径路关系,首先根据道岔结构,梳理咽喉区合理径路。咽喉区径路如图1所示,以接车进路为例,连接到发线9股道、10股道的咽喉区径路为V5→V1→J9/J10；连接到发线7股道、8股道的咽喉区径路包括2条,V5→V1→V3→J7/J8和V5→V7→V3→J7/J8,前者与接车进路V1→J9/J10产生交叉干扰,不利于车站采用平行进路进行作业,将这类进路称为“不合理进路”,并且在实际作业中也不会采用。在列车进路分配时不考虑这一类进路。

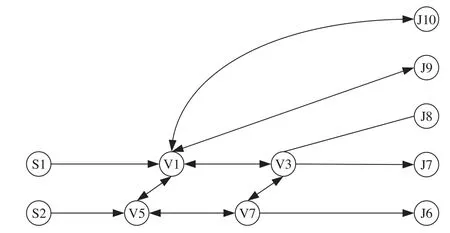
图1 咽喉区径路Fig.1 Throat paths

当确定是到达进路或出发进路时,1条到发线只对应1条合理咽喉区径路,而1条咽喉区径路可能对应1 ～ 2条到发线。因此,通过分析所有合理咽喉区径路冲突关系后,则到发线之间的关系也确认了(当1条咽喉区径路对应2条到发线时,这2条到发线是冲突关系)。对于出段进路和入段进路,由于接入相同到发线的发车和接车进路中,必有一个道岔组是相同的,因而同样可以用到发线敌对关系来反映咽喉区径路敌对关系。为优化进路分配模型的复杂度,直接采用到发线关系来反映咽喉区径路和列车进路相互关联性。

1.2.2 进路分配模型

假设：①高速铁路车站各项作业时间标准已知；②不考虑轨道电路分段解锁,以道岔分组确定列车进路之间的关系；③忽略同一作业过程占用不同长度进路所需时间差异；④不同种类列车对数不做要求。在满足车站作业间隔时间约束条件下,以2列相邻列车作业间隔时间最小为优化目标1,使得到发线尽可能多的排列到发列车,计算公式如下。

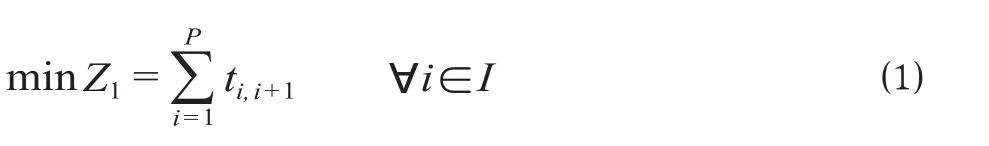
式中：Z1为2列相邻列车作业间隔时间,min；ti, i+1为任意2列相邻列车作业间隔时间,min；I为车站在某一时间域内接发列车集合,按照列车开始占用到发线先后顺序进行排序,记为I= {1,…,i,…,P},P为列车总数。

在公式 ⑴ 优化目标基础上,利用平行进路作业间互不干扰的特点,以具有平行作业关系的到发线的利用率最大为第2优化目标,对已有方案进行调整,使得始发终到站能力达到最大,计算公式如下。

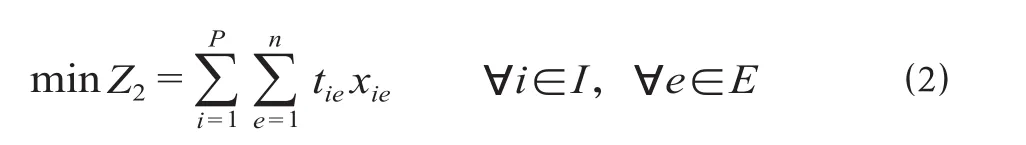
式中：Z2为具有平行作业关系的到发线的利用率,%；tie为列车i在平行进路所在到发线e的停留时间, min；xie为决策变量,当列车i占用平行进路所在到发线e时,xie= 1,否则为0；平行进路占用到发线集合为E,E= {1,…,e,…,n},总数为n。

其中,约束条件如下。

（1）任意1列车只能占用1条到发线,计算公式如下。

式中：xij为0-1决策变量,当第i列列车占用到发线j时,xij为1,否则为0。

（2）同一到发线任意2列车的间隔时间不小于到发线安全使用时间,计算公式如下。

式中：i,y为任意2列车,为0-1决策变量,当第y列列车占用到发线j时,xij为1,否则为0；J为车站到发线集合,J= {1,…,j,…,m},m为到发线总数(E∈J),计算公式如下。

以某高速铁路车站A的方向B为例,由于B

式中：为列车y的到达时间；为列车i的出发时间；tg为相邻2列车占用到发线的最小间隔时间。

（3）相互干扰列车进路到发间隔时间约束。

①到达—出发间隔时间约束条件,计算公式如下。

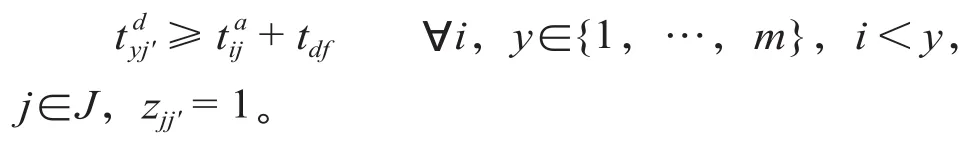
式中：为列车y从到发线j'的出发时间；为列车i到到发线j的到达时间；tdf为冲突股道之间两列车到达—出发最小间隔时间。

②出发—到达间隔时间约束条件,计算公式如下。

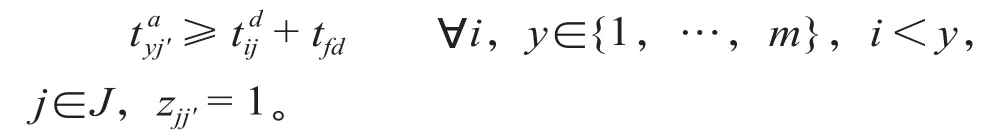
式中：为列车y到到发线j'的到达时间；为列车i从到发线j的出发时间；zjj'表示股道之间的关系,当股道j和j'是冲突关系时,zjj'为1,否则为0；tfd为冲突股道之间两列车出发—到达最小间隔时间。

（4）同一方向列车仅在其可占用到发线上作业,计算公式如下。

式中：cij表示若列车i可以占用到发线j,则cij= 1,否则cij= 0。

在以能力最大进行列车进路分配时,不存在缓冲时间和客运组织等因素影响,不对这方面进行约束。

2 案例分析

方向的往返列车只能在车站左侧咽喉区径路办理作业,通过对该站A左侧咽喉区进行道岔分组,得到高速铁路车站A平面图如图2所示。

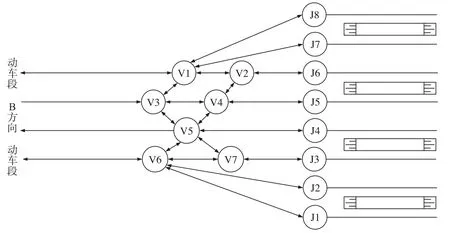
图2 高速铁路车站A平面图Fig.2 Plan of high-speed railway station A

在图2中,J1—J8表示到发线1至8；V1—V7表示咽喉区道岔组。以A站为研究对象,由于A站去往目标方向的列车只能从左侧咽喉区办理接发列车作业,当以能力最大化进行列车进路安排时,由于不同速度等级列车各项作业时间差距很小,因而按照同一速度等级列车进行进路分配,并且作业列车主要包括折返列车、始发列车、终到列车3类,根据现场调研和《高速铁路设计规范(TB10621—2014)》,高速铁路车站不同列车作业时间标准如表2所示。

表2 高速铁路车站不同列车作业时间标准 minTab.2 Time standard for different train operations in high-speed railway station

根据该站咽喉区径路和到发线平面图,以及上述3种列车的主要列车作业,去除“不合理进路”,得到可行列车进路,高速铁路车站列车进路表(只显示部分进路和到发线关系)如表3所示。

由于发到和到发列车进路间隔时间的约束,首先梳理接车、发车进路中的平行和敌对进路,根据第2部分叙述可知,当确定是到达进路或出发进路时,咽喉区径路冲突关系确定后,则到发线之间的关系也确认了,因而采用到发线来表示进路冲突关系。通过分析可知,高速铁路车站到发线平行作业关系如表4所示,高速铁路车站到发线敌对作业关系如表5所示。

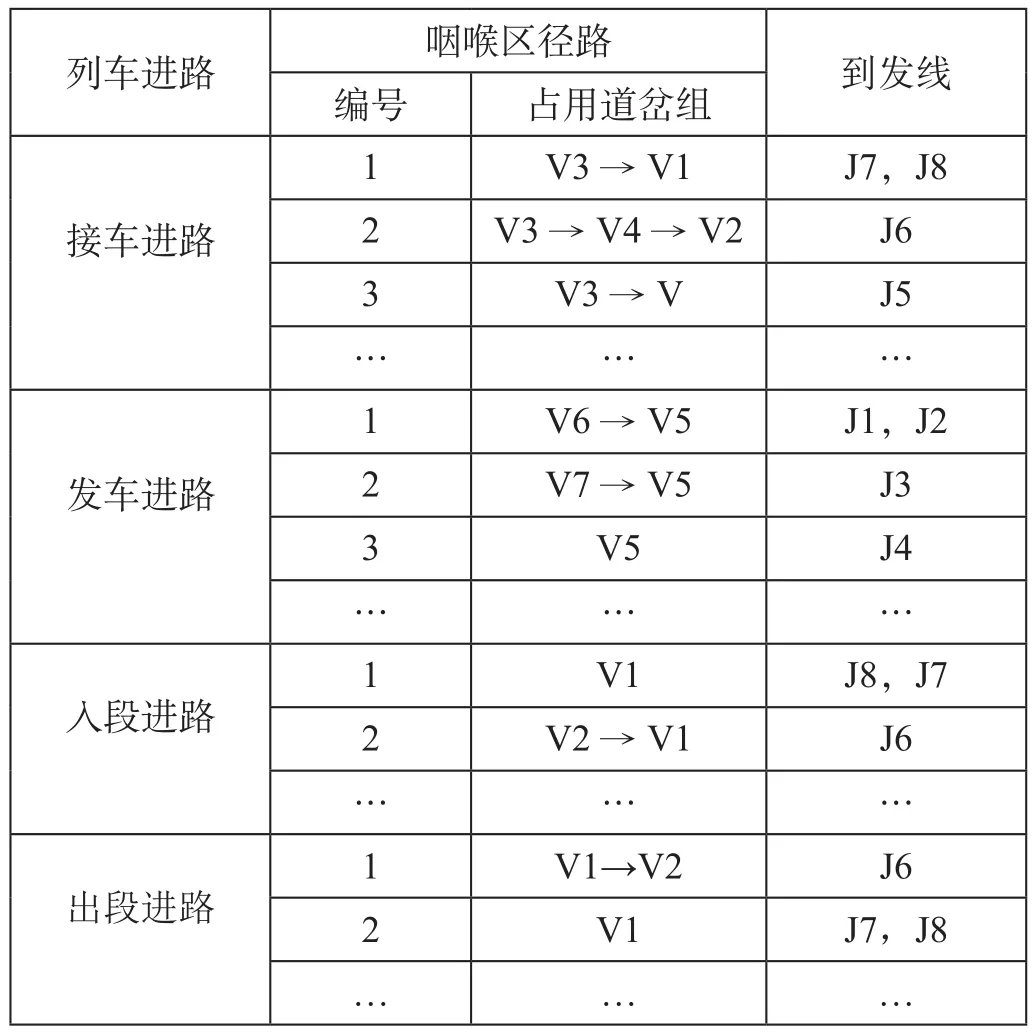
表3 高速铁路车站列车进路表Tab.3 Train routes for high-speed railway stations

表4 高速铁路到发线平行作业关系Tab.4 Parallel operation relationship between arrival and departure tracks of high-speed railway

表5 高速铁路到发线敌对作业关系Tab.5 Adversarial operational relationship of arrival-departure tracks of high-speed railway

该模型求解过程主要包括2个步骤：①初始方案。首先生成以列车作业间隔时间最小的进路分配方案。②调整方案。利用平行径路与其他径路接、发车作业互不干扰的特点,以平行作业关系的到发线的利用率最大为目标,对上一阶段方案进行调整,实现高铁站能力利用最大化。采用LINGO软件对模型进行求解。

按照相邻2列出发列车间隔时间5 min,相邻2列到达列车间隔时间5 min进行能力最大化的列车进路分配,并以1 h为周期编制能力最大的列车进路分配方案,A站能力最大运用方案如表6所示,A站能力最大运用方案如图3所示。

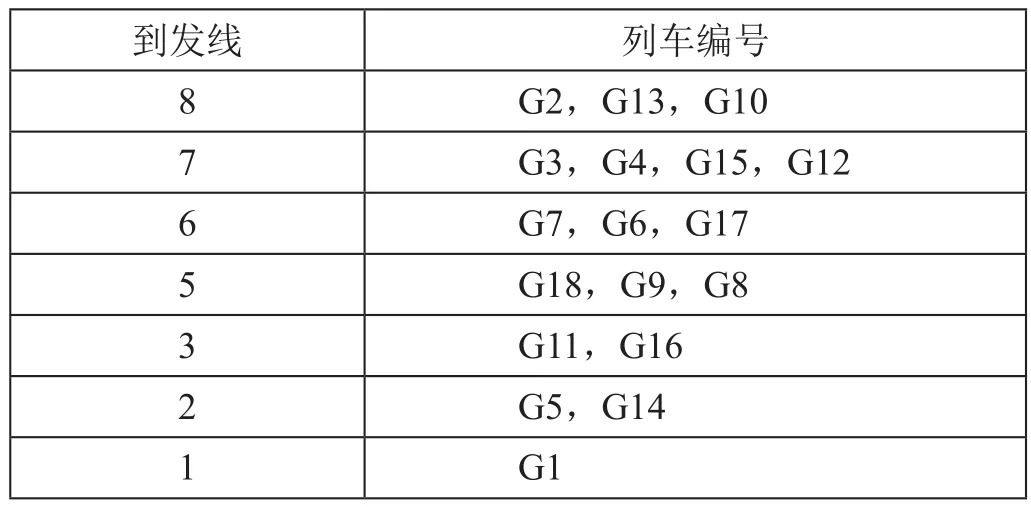
表6 A站能力最大运用方案Tab.6 Maximum capacity plans of station A

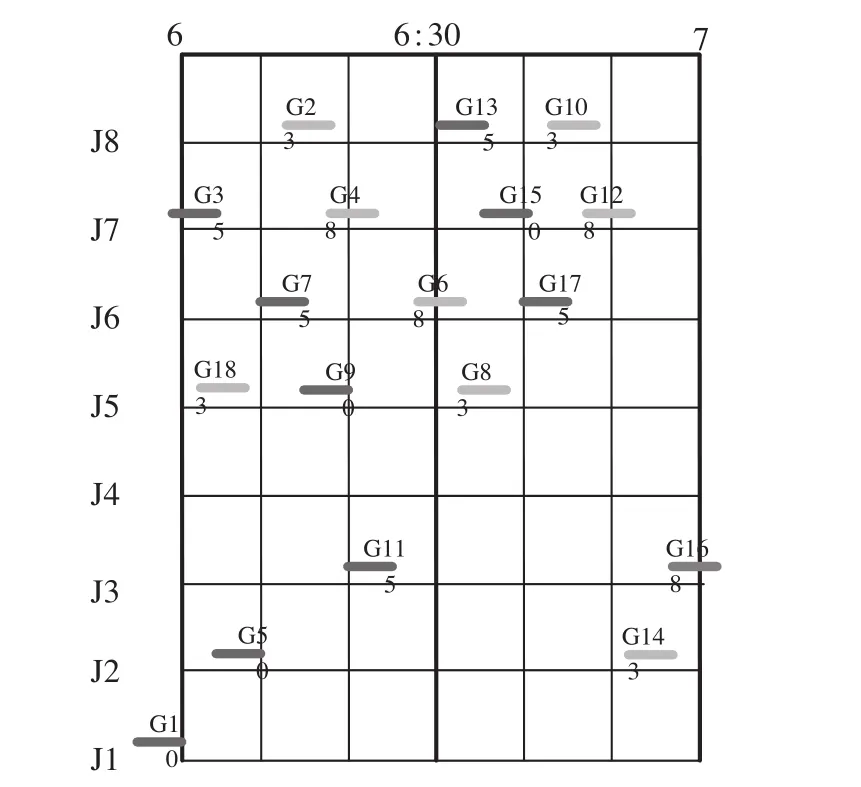
图3 A站能力最大运用方案Fig.3 Maximum capacity plans of station A

从图3中A站到发线占用方案看出,在6 : 00—7 : 00周期内,共有8对列车,其中折返列车7对,始发列车2列(G17,G1)、从动车段出发到达到发线,终到列车2列(G10,G8)、从到发线驶入动车段。按照日间高速铁路时间可行域为[6 : 00,24 : 00],因而可算出A站的到发线能力为144对/d。相比前期调研结果,枢纽站能力提升了25%,从而验证模型的合理性和方法的可行性。

3 结束语

随着我国高速铁路通过能力点、线协调问题日益突出,准确计算高速铁路车站通过能力,对于充分挖掘车站设备潜力、优化枢纽站运输组织、提高铁路运输管理效率以实现高速铁路点线能力协调十分重要。采用高速铁路车站列车进路分配模型后,不仅有利于车站能力提升,而且形成了车站能力的有效计算方法。由于研究得到的高速铁路车站能力最大值未考虑与区间线路能力的协调性和客流需求的影响,还有待对枢纽和通道能力协调利用进一步研究。