混合动力复合翼应急迫降在线航迹规划与制导
王子安,龚正,陈永亮,史志伟,徐锦法
南京航空航天大学 航空学院,南京 210016
复合翼飞行器兼具多旋翼结构简单、垂直起降无需跑道与固定翼长航时的优点,广泛应用于远距离侦查测绘、应急物流投送领域,并逐渐大型化。中型以上采用混合动力方案的复合翼,其旋翼系统采用高放电倍率锂电池独立供电,巡航采用活塞发动机提供推力与电力。在运营过程中,飞行故障主要出现在活塞发动机过热、油路堵塞等造成的空中停车事故。这类空中停车问题往往无法通过重新电启动恢复动力,但旋翼系统不受影响。因此可以通过自主完备的迫降程序进行自动应急处置。
复合翼的特点决定了其巡航模式下空中停车应急迫降与以往的常规固定翼无动力应急返场[1-3]、直升机迫降有一定区别。首先,与常规固定翼应急返场相比,应急迫降点的选择不受机场条件限制,在任务规划中可以沿预定航线附近寻找多个开阔地面作为应急迫降点。复合翼飞行全程到最近迫降点大多具备较富余的势能,应急航线自主规划重点在于耗散能量与对准着陆入口。其次,与直升机/旋翼机迫降相比,复合翼着陆前必须完成从固定翼模式向旋翼模式的转换,这需要一定长度的空中走廊。考虑到避障等因素,复合翼必须沿着预定方向切入走廊的入口,而非直升机直接趋向迫降点。因此,应急着陆航线的实时在线规划以及精确制导跟踪是复合翼无动力应急迫降的关键技术。
针对应急着陆航迹在线规划,许多学者将此转化成在指定优化指标下满足动力学约束、状态约束、几何约束的非线性规划问题,运用序列二次规划(SQP)或凸优化等工具数值求解[4-8]。如唐鹏和张曙光[6]、作者团队龚正[7]基于几何规划及高度推演的方法给出了可重复使用运载器末端能量管理(TAEM)的在线轨迹优化方法;王宏伦等[8]对固定翼着陆轨迹进行分段建立优化指标,采用hp自适应伪谱法求解,但这些方法计算量大,难以保证机载计算机实时、可靠的航迹求解。另一类实时规划算法如A*算法[9-10]、快速扩展随机树(RTT)算法等能根据当前复杂地理环境信息高效搜索空间随机采样点,生成满足几何约束及动力学约束的航迹,但这些方法适合复杂环境的航迹规划,并不适用于应急返场等大空域下简单几何约束的航迹在线规划。2D Dubins航迹由圆弧和直线组成,是描述固定翼航向机动最简单的规划曲线。3D Dubins航迹是在2D Dubins航迹基础上进行高度推演并满足爬升、下滑、速度静稳定性能约束的三维航迹[11]。由于航迹角、终端位置/航向的显性约束,使得3D Dubins曲线非常适合应急航路的航迹规划。
针对精确制导跟踪应急航迹,所提的制导律应当具有较强的鲁棒性,且具备抵抗侧风/阵风与三维航迹跟踪能力。Eng等[12-13]改进Park等[14]横航向L1制导律,在设计制导律时考虑了风场信息,将无人机跟踪圆弧轨迹的误差方程做合理简化,简化了制导律结构,但此类航路点跟踪的制导算法无法获取航迹曲率的完整信息,当航迹曲率变化较快、较大时,其跟踪性能将大打折扣。Furieri等[15]在Cho等[16]基础上设计抵御任意强风制导策略。非线性模型预测控制(NMPC)是一种基于模型的闭环在线优化控制策略,正逐步应用到无人机航迹规划、制导控制等领域[17-23]。Stastny等[17]最早将NMPC应用于固定翼无人机的航迹跟踪。Yang等[21]扩展了Kang和Hedrick[19-20]的工作,提出自适应NMPC制导算法,通过在滚动时域内迭代更新参考航迹曲率,并在目标函数引入控制输入速率饱和限制以达到对控制输入震荡抑制、精准制导及避障功能。
本文主要研究混合动力复合翼巡航飞行空中停车后无动力应急迫降的在线航迹规划与制导问题。本文通过在2D Dubins平面曲线简单、高效的几何特征的基础上简单高度拓演,即可规划出满足复合翼动力学约束的3D Dubins航迹。同时,根据返场初始点高度、横向位置、航向的不确定散布,考虑下滑性能约束,通过应急返场航路管理单元将下滑航迹划分为标准下滑、S-Turn机动转弯、螺旋机动增程等类型。针对复合翼应急迫降航迹跟踪易受风干扰以及3D Dubins 航迹曲率不连续的特征,给出一种基于非线性模型预测控制的三维制导算法,将结合先行向量的横纵解耦制导律嵌入预测模型框架内,外界风扰动、航迹曲率不连续等非线性因素通过系统输出约束建模,并滚动优化实时求解。最后对航迹在线规划方法与制导律的适应性进行仿真分析。
1 复合翼应急迫降运动方程
假设某大型油电混合复合翼巡航飞行时由于活塞发动机油路堵塞造成空中停车,但独立供电的旋翼动力系统不受影响,需滑翔迫降到在参考航线沿线预设的迫降窗口,以旋翼模式减速降落至最佳着陆场,如图1所示。这类在升限10 km,飞行速度300 km/h以下的飞行器飞行包线窄、初始能量状态散布小且对模型气动参数不敏感,其纵向剖面只需通过简单的下滑角限制即可满足下滑性能约束,其横向机动受高度变化影响小,具备在平面航迹基础上进行高度推演的航迹规划的条件。
假设空中停车后,复合翼处于小迎角纯固定翼模式滑翔,并用一阶惯性环节表征内回路的动态特性,则可简化成三自由模型:

图1 油电混合复合翼飞行器应急迫降示意图
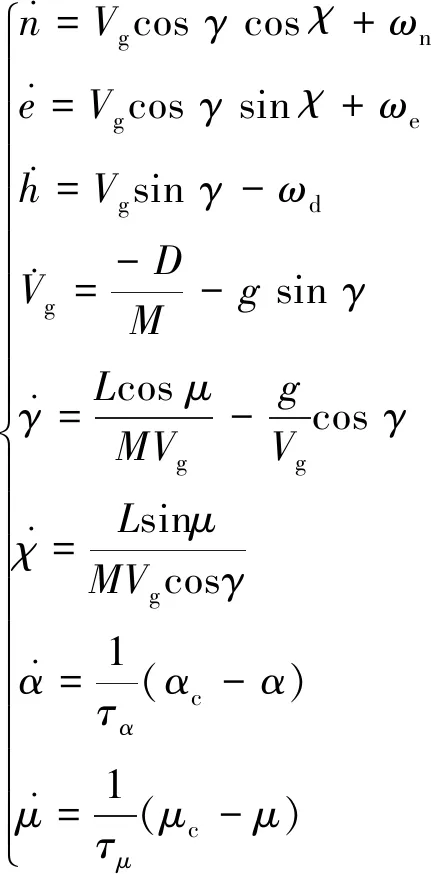
(1)

(2)
式中:CD0、CL0分别为零升阻力系数与零升系数;CLα为升力系数斜率;CL为升力系数;A为升致阻力因子。
2 3D Dubins航迹设计
3D Dubins 航迹规划方法旨在在线生成一条从初始位置/航向Ps=[ns,es,hs,φs]到终端位置/航向Pe=[ne,ee,he,φe]并满足滚转角与下滑角限制的最简航迹。
2.1 2D Dubins航迹设计
在给定的位姿点下,标准2D Dubins由航路点Ps→P1→P2→Pe构成,Ps为返场初始点,P1为航向调整圆Cs切出点,P2为航向对准圆Ce切入点,Pe为航向对准圆Ce切出点,P4为进场末端点。整个横向航迹可划分为航向调整段Ps→P1,返场直线段P1→P2,航向对准段P2→Pe,进场直线段Pe→P4,如图2所示。文献[24]给出求解2D Dubins曲线的解析几何法与微分几何法,所解得4条航迹中的最短航迹定义为本文的2D Dubins航迹。

图2 标准2D Dubins航迹
Ps→Pe段航程记为L2D,Ps→P1(P2→Pe)段航程记为LRs(LRe),P1→P2段航程记为Lse,则满足:
L2D(Ps(φs),Pe(φe))=LRs+Lse+LRe
(3)
式中:LRs=Rs|Δφs|,LRe=Re|Δφe|;Δφs(Δφe)为Ps→P1(P2→Pe)的方向偏角;Rs和Re分别为航向调整圆和航向对准圆的滚转半径。
2.2 3D Dubins航迹设计
复合翼高度/马赫数范围受限,真空速变化比较窄,速度较低,航向机动性较强,可假设复合翼空中停车后,能以恒定的滚转姿态协调转弯,并以恒定下滑角飞行,则3D Dubins航迹可以在2D Dubins平面航迹的基础上进行高度推演。受横向机动航程及下滑性能约束,复合翼的下滑坡度受限。当复合翼初始高度过低(过高)时,常规的高度推演法则无法覆盖这些场景下的应急航迹规划。因此,本文提出在无动力飞行性能约束下的在线航迹规划方法,通过增加或缩小横程等手段解决不同高度、不同进场航向角的应急航迹规划适应性问题。
根据复合翼返场高度差与标准横程、下滑角约束γ∈[γmin,γmax](γmin为最陡下滑角,γmax为最浅下滑角)的对应关系,分成4种下滑类型:浅下滑类型、标准下滑类型、S-Turn机动转弯类型、螺旋机动增程类型。当复合翼以最浅下滑角下滑,使得进场高度过低,满足式(5),此时需要通过改变进场点位置缩小横程,称其为浅下滑类型;当复合翼以标准的高度拓演法满足下滑性能要求,满足式(6),称其为标准下滑类型;当返场高度差较大,复合翼无法通过Dubins平面横程以最陡下滑角下滑到进场高度,但此时多余高度差又无法按最小盘旋半径与最陡下滑角进行整圆高度耗散,满足式(7),此时需要以航天飞机末端能量管理S-Turn转弯的方式,通过机动转弯增加横程以减弱下滑坡道的斜率,称其为S-Turn机动转弯类型;当复合翼飞行高度太大,满足式(8),此时需要复合翼在末端绕能量柱,以螺旋机动下降的方式耗散多余能量,称其为螺旋机动增程类型。
Dse=LRstan|γs|+LRetan|γe|
(4)
|he-hs|≤Lsetan|γmax|+Dse
(5)
Lsetan|γmax|+Dse<|he-hs|≤
Lsetan|γmin|+Dse
(6)
Lsetan|γmin|+Dse<|he-hs|<
Lsetan|γmin|+2πRetan|γe|+Dse
(7)
|he-hs|≥Lsetan|γmin|+2πRetan|γe|+Dse
(8)
式中:Dse为航向调整圆与航向对准圆高度损失和;γs和γe为航向调整圆与航向对准圆的下滑角。
2.2.1 标准3D Dubins航迹
假设复合翼在最初与最终转弯时,下滑角均按最佳下滑性能(最小高度损失航迹)设计,则平衡滑翔条件下其滚转角与下滑角满足:
(9)
式中:Vs为滑翔下沉率;Vg/Vs≈L/D,L/D为升阻比;φs和φe为航向调整圆与航向对准圆滚转角。
航向调整段Ps→P1和航向对准段P2→Pe高度损失Δhs、Δhe为
(10)
航向调整圆切出点P1与航向对准圆切入点P2的高度h1、h2为
(11)
返场直线段的下滑角γl为
(12)
标准3D Dubins航迹平面航迹横程为L2D(Ps(φs),Pe(φe)),对应航程高度H为
H=LRstan|γs|+LRetan|γe|+Lsetan|γl|
(13)
2.2.2 S-Turn机动转弯航迹
文献[7]针对航天飞机的末端能量管理,选择动压-高度预案后,以蛇形机动原理与轨迹推演在线优化生成满足过载、动压等约束的轨迹。本文借用其思想,通过在末端转弯圆处增加额外的反向相切转弯圆(当航向对准圆为左(右)转圆时,则插入右(左)转圆)以增加Dubins平面航迹,从而使高度拓演满足式(7)。如图3所示,Ps→P1为航向调整段,P2→P3→Pe为航向对准段。其算法步骤如下:
步骤1设终端点Pe绕航向对准圆Ce(Re)反转φe′角度后插入反切圆,切点记为P3,此亦是新的终端点,见式(14)。新航向对准圆为C1(Re),其与初始点Ps组成新的标准2D Dubins平面航迹{Ps,P1,P2,P3}。
P3=Ce+Re(-φe′)(P3-Ce)
(14)
步骤2机动转弯增程的Dubins平面航迹航程L(φe′)为
L(φe′)=Reφe′+L2D(Ps(φs),P3(φe-φe′))
(15)
为减小自变量,假定返场直线段P1→P2按最陡下滑角下降,则拓演的高度H(φe′)为
H(φe′)=Reφe′tanγe+Dse+Lsetan|γmin|
(16)
步骤3针对初始转弯角φe′求解,本文采用数值二分解法,使得不等式(17)成立,进而求解φ*≈φe′。
|H(φ*)-|he-hs||≤δ
(17)
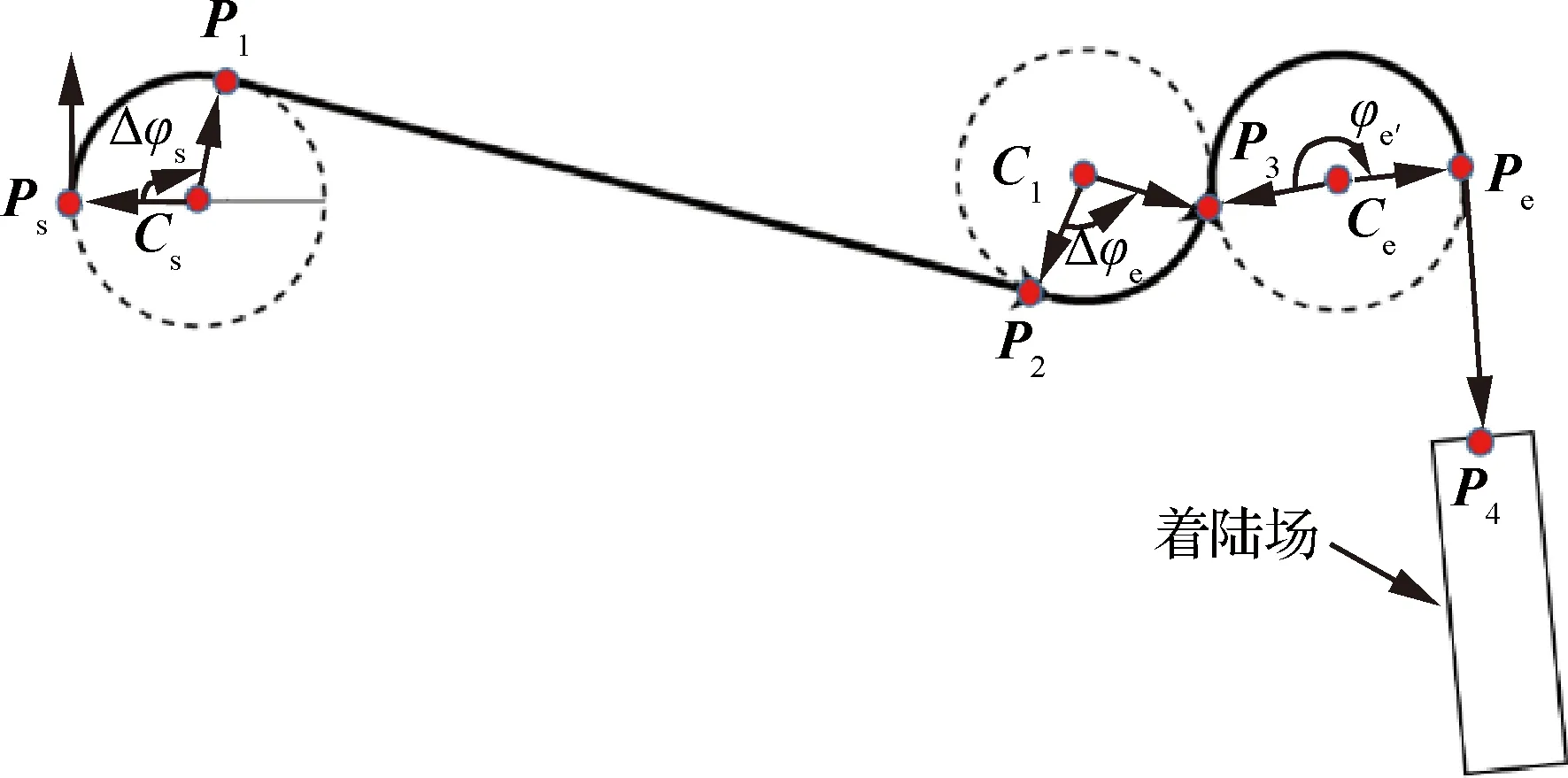
图3 S-Turn机动转弯平面Dubins航迹
2.2.3 螺旋机动增程航迹
文献[13]针对飞行高度过高的能量耗散问题,采用盘旋下降的方式在初始转弯处进行垂直高度调整,对无法通过整圆盘旋的末端剩余高度,采用桥接的手段,通过增大末端1/4段盘旋圆弧的下滑角,将该剩余高度嫁接到该段圆弧,但该段圆弧不受下滑性能约束。本文采用在航向对准段实施S-Turn机动转弯以及在末端实施螺旋机动组合方式耗散多余高度。
如图4所示,Ps→P1→P2→P3→Pe′为S-Turn机动转弯段,Pe′→Pe为由ξ个整圆构成的螺旋航迹迹。其算法步骤如下:
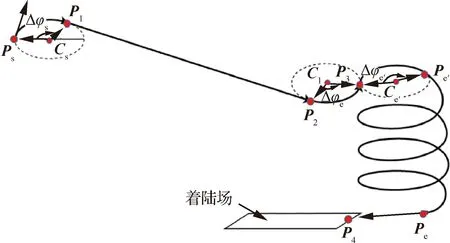
图4 螺旋机动增程航迹
步骤1获取螺旋机动高度耗散的整圆圈数ξ,Pe′→Pe螺旋段耗散的高度为2πξRetan|γe|,即

(18)

步骤2新的终端点为Pe′,其与初始点Ps的高度差满足式(19),新的终端点高度he′满足式(20)。Ps→Pe′组成新的S-Turn机动转弯航迹,需按S-Turn机动转弯类型解算剩余航迹信息。
Lsetan|γmin|+Dse≤|he-hs|-2πξRetan|γe|<
Lsetan|γmin|+2πRetan|γe|+Dse
(19)
he′=he+2πξRetan|γe|
(20)
2.3 复合翼应急返场航路管理
在选择到合适的着陆场后,航路在线规划管理单元初始化复合翼初始与终端的位姿状态,并应用3D Dubins 路径规划算法规划出一条可达的三维航迹,其详细流程如图5所示。
首先,设定进入航向调整圆与航向对准圆滚转角φs和φe,转弯半径为Rs和Re,按文献[24]中方法进行2D Dubins存在性判别。若横向平面无法构造Dubins几何航迹,则按单段航迹直接迫降;反之,按照算法1进行高度拓演。若返场直线段下滑角γl满足下滑角约束,则直接生成三维Dubins航迹;若γl超出约束,则进入下一层级判别。若返场高度不满足式(8),则按算法2生成螺旋机动增程航迹;若返场高度满足式(8),则按算法3生成S-Turn机动转弯航迹。
3 非线性模型预测制导
(21)
(22)
式中:r为当前位置;P为航线参考点;τ为权值系数,0≤τ≤0.5π,τ的大小决定了先行向量是侧重消除位置误差还是方向误差。

3.1 参考点位置
类似螺旋机动增程航迹取整圆法,三维Dubins螺旋线参考点获取方式为先获取横向剖面的参考位置,再在垂直剖面进行高度拓演获得参考点垂直高度(直线部分较为简单,此处不予论述),如图6所示。图中:C为P所在横向剖面投影圆的圆心位置;Ra为圆C半径;b为螺旋线终端位置;m表示点b绕螺旋线m个整圆到达b′m点,令b′m={b′1,b′2};Δφ为b′2到P的方向偏角;Δhφ为b′2沿螺旋线转角Δφ至P点的高度差;Δhm为从b到b′2的高度差;γa为下滑角。
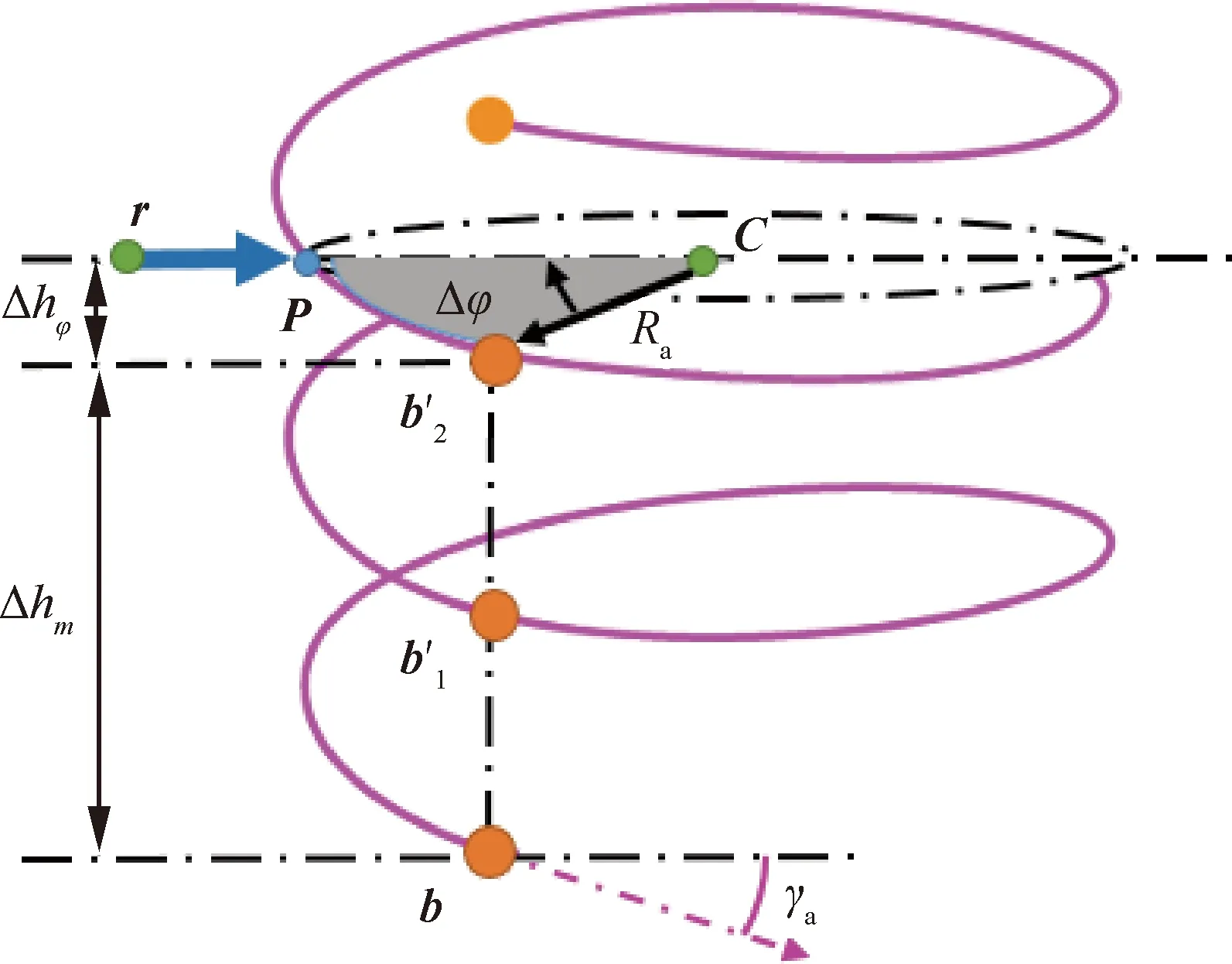
图6 三维Dubins螺旋段参考点
P点的横向位置nP,eP为
(23)
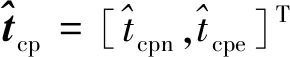
以b为基准点,由式(24)~式(26)可得P点垂直高度hP。
Δhm=2πRamtan|γa|
(24)
Δhφ=ΔφRatan|γa|
(25)
hP=hb+Δhm+Δhφ
(26)

3.2 横航向制导律
横航向制导几何逻辑如图7所示,横航向制导律需要同时兼顾侧向偏差与偏航角误差,则先行矢量线性形式:
(27)

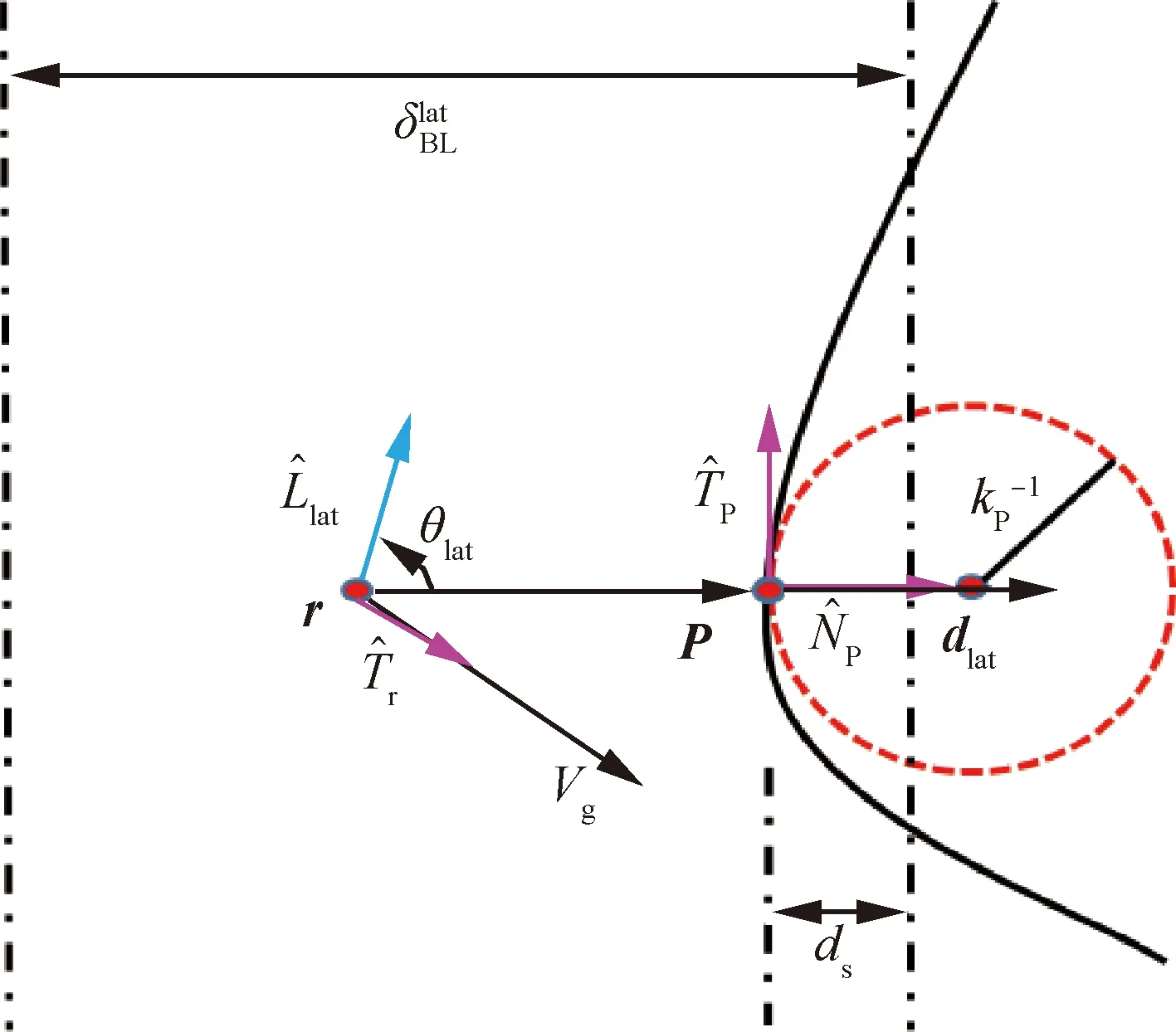
图7 横航向制导几何逻辑
如图7所示,引入径向移动距离ds,以保证复合翼具备平稳的转向机动及能渐进逼近参考航迹,则dlat的两个元素dn和de的表达式分别为
(28)
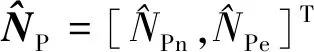
先行角θlat的映射函数需要满足以下条件,以实现轨迹跟踪的先行效应。

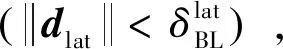
条件3在边界层内,复合翼需要平滑导引至参考路径,且相应的制导指令幅度变化小。
(29)
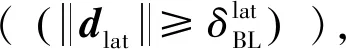
(30)
则前向角函数选择为
(31)
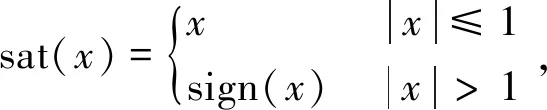
NMPC形式的横向制导误差输出定义为
(32)
式中:ηlat为横航向角度误差。
3.3 纵向制导律
纵向制导律需要同时兼顾纵向偏差与航迹倾角误差,类似横向制导律,纵向亦引入先行矢量,其线性形式为
(33)
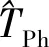
类似横航向的制导误差输出,NMPC形式的纵向制导误差输出定义为
(34)
式中:ηlon为纵向角度误差。
考虑三维轨迹跟踪的横纵跟踪协调性以及位置误差的显性表示,引入位置误差项ηe[17],其形式为
(35)
式(35)与纵向角度误差ηlon,横向角度误差ηlat构成了系统误差输出向量Y=[ηe,ηlon,ηlat]T。
3.4 航迹段切换条件
3D Dubins航迹由圆弧段(螺旋线)与直线段构成,其装订集合为
(36)

圆弧段:
Darc={na,ea,ha,χa,Δφab,λ,Ra,γa}
(37)
直线段:
Dline={ns,es,hs,ne,ee,he}
(38)
式中:a=[na,ea,ha]T为圆弧段圆心坐标;ha为圆弧段起点高度;χa为圆弧段起点航迹偏角;Δφab为圆弧段起点到终点的方向偏角;λ={-1,1}分别代表逆时针方向与顺时针方向;Ls=[ns,es,hs]T与Le=[ne,ee,he]T分别代表直线段起始与终端航路点。

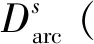
(39)
SPb<ε2
(40)
式中:SPb为P沿当前航线至b的距离;ε1为切换至下一航迹段的待飞径向距离;ε2为切换至下一航迹段的待飞航线距离。
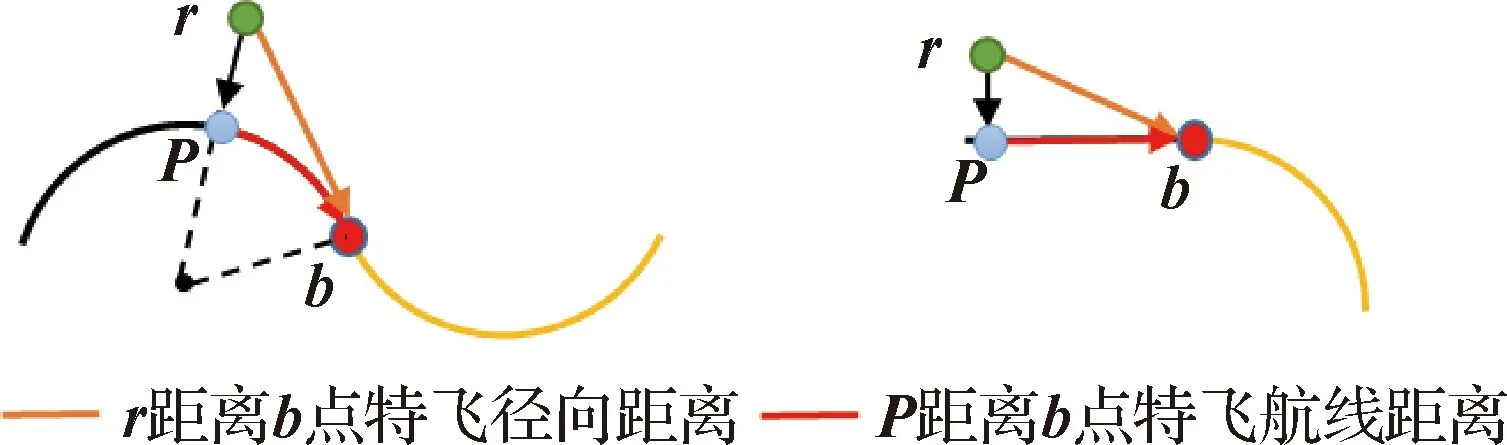
图8 航迹段切换条件
另外,在大空域返场时预测窗口内预测状态通常处于对单段航迹导引,邻近航迹末端才满足切换条件(式(39)和式(40))。可按参考点P以当前速度沿航迹段经预测时域T后点P′位置预判预测模型是否嵌入切换条件,从而降低目标函数的非线性程度。若复合翼当前位置r跟踪圆弧段(直线段),P′仍在圆弧段(直线段),不满足式(41),则预测模型无需嵌入切换条件(式(39)和式(40)),如图9(a)和图9(b)所示;反之,预测模型内部嵌入切换条件(式(39)和式(40)),如图9(c)和图9(d)所示。
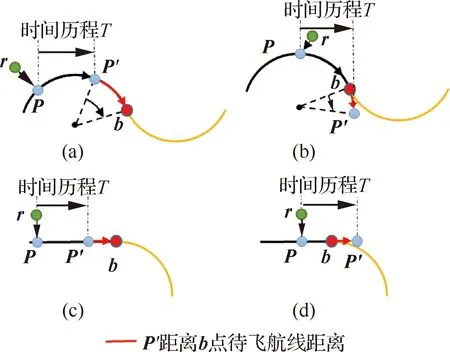
图9 预测模型嵌入切换条件判别
SP′b<ε3
(41)
式中:SP′b为P′沿当前航线至点b的待飞航线距离;ε3为切换至下一航迹段的预判待飞航线距离。
3.5 优化目标函数
目标函数J(X)是以当前状态为初值,选择二次型形式,通过有限时域性能指标构造的正定函数。复合翼非线性模型预测制导目标函数表示为
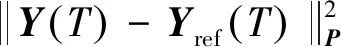
(42)
3.6 NMPC制导算法描述
详细 NMPC 制导算法由以下5个步骤多次迭代到收敛完成。

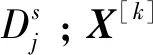


步骤5令k=k+1,重复步骤1~步骤4。
4 仿真分析
4.1 3D Dubins航迹适应性规划
为验证应急返场航路管理单元对不同高度,不同航向应急返场的适应性。假设复合翼应急迫降初始点Ps=[ns,es]=[-2 072.2 m,118.67 m],终端点Pe=[ne,ee,he,φe]=[0 m,0 m,0 m,0 rad],初始航向调整圆与末端航向对准圆的半径为Rs=Re=320 m,下滑角为γs=γe=-10°,并假定复合翼下滑角约束为γ∈[-10°,-2°],设置初始高度hs分别为200、1 000、3 000 m,令其满足式(6)~式(8)(暂不考虑进场距离),同时选取一组以固定间隔的航向角φs=0:π/9:2π,针对选择每一个航向角,根据应急返场航路管理单元得到标准3D Dubins航迹,S-Turn机动转弯航迹,螺旋机动增程航迹,如图10~图12所示。
图10展示了初始点在同一高度与横向位置,不同航向角的标准3D Dubins航迹,各个航迹直线段的下滑角γl限制在[-4.755°,-2.499°]之间,满足下滑角约束。图11展示了同一高度不同航向情况下应急返场航路管理单元能规划出不同类型的机动航迹,绕右边Hac圆的航迹(横程短)选择螺旋机动增程航迹耗散能量(高度),而绕左边Hac圆的航迹(横程长)通过S-Turn机动转弯航迹耗散能量(高度)。图12展示了初始点高度过高,只能规划出螺旋机动增程航迹的情况,其各个航迹的航向对准Hac圆跟初始点的航向位置相关。

图10 航向不确定下的标准3D Dubins航迹
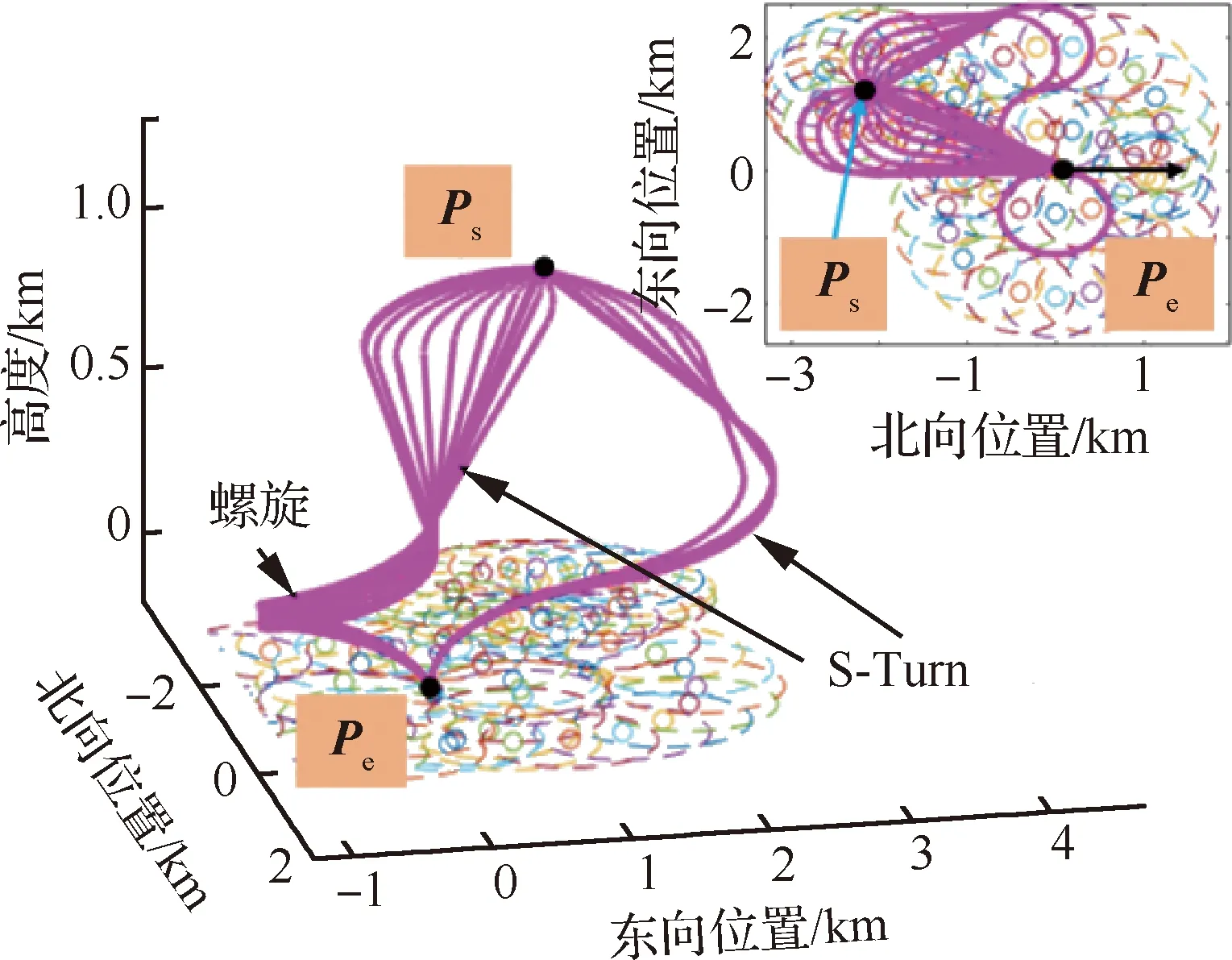
图11 航向不确定下的S-Turn机动转弯航迹

图13 横向位置不确定下的3D Dubins下滑航迹
图13展示了初始点在同一高度与航向,不同横向位置的3D Dubins航迹适应性规划。图中初始点的横向位置等间距散布在终端点Pe右半区域,其中粉色曲线集合构成标准机动类型航迹族,黑色曲线集合构成S-Turn机动转弯航迹族,红色曲线集合构成螺旋机动增程航迹族。从右上水平投影图各航迹族的分布区域可知,在远离终端点Pe的横向区域由标准机动类型航迹包络,中间横向区域由S-Turn机动转弯航迹包络,最近横向区域螺旋机动增程航迹包络。各种航迹的散布符合横向几何增程的原理,可知,经由下滑角约束的高度判别的应急返场航路管理单元可进行横向位置散布的适应性规划。另外,当初始点距离终端点太近无法满足2D Dubins航迹存在条件[24],则需按单段螺旋线终端导引。在实际工程中,可在地面站合理设置多个相应迫降区域规避单个不能通过Dubins导引的区域,做到应急区域全覆盖。
4.2 应急着陆航迹跟踪仿真
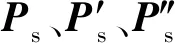
复合翼滚转角约束,下滑角约束通过在顺风、逆风、下降风干扰及不同滚转姿态下的平衡滑翔速度极曲线获得,如图15所示。图中过坐标原点且与速度极曲线相切的曲线斜率的反切值为最浅下滑角,此时的飞行速度为中立稳定。在此状态飞行,顺风、上突风以及较大的滚转姿态都会使飞机进入速度静不稳定区(正区)。因此,可通过对下滑角的约束将下滑速度约束在速度静稳定区(反区)内。同时,所选择的下滑角区间应使飞机下滑时具有一定的减速能力,由定直平飞下最远平衡下滑速度为23 m/s,对应下滑角为-5.3°,则选择下滑角区间为γ∈[-10°,-6°],其位于速度反区内。其次,滚转姿态易引起速度极曲线整体下移,并且滚转角越大为维持协调滚转所需的法向过载越大,由图15可知,应选取对下滑性能影响较小的滚转区间φ∈[0°,40°]。飞行器的巡航速度为30 m/s,全机最大升阻比为10.2,设置转弯的滚转角为30°,其滚转半径Rs=Re=159 m,由式(9)得平衡下滑角约为-7°。应急返场航路管理单元分别规划出3条应急航线,其中
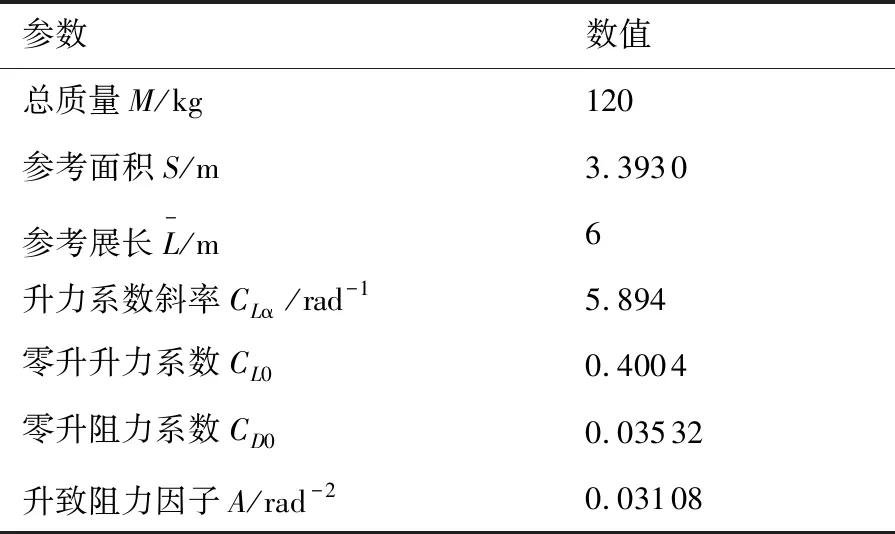
表1 复合翼主要参数
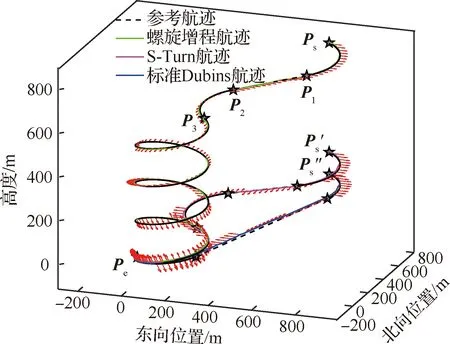
图14 不同方向风场干扰下的航迹跟踪效果
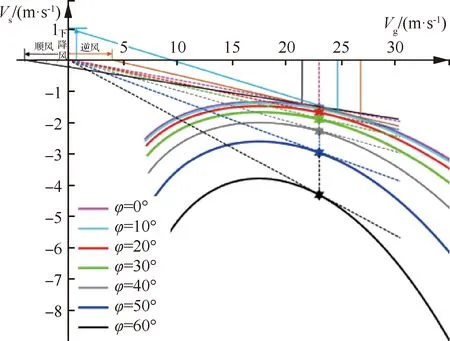
图15 在顺风、逆风、下降风干扰与不同滚转姿态下的平衡滑翔速度极曲线

现考察非线性模型预测制导在随机常值弱风干扰下的制导效果。制导的预测模型选择式(1),系统带宽为3 rad/s,系统采样周期为100 ms,预测步长N=30,最小控制输入Umin=[-2°,-40°]T,最大控制输入Umax=[10°,40°]T。系统所受阵风ω=3 m/s,风向由北→南→西→东→下→上依次转变。复合翼受弱风扰动的航迹跟踪效果如图14所示。图14中,红色箭头部分代表矢量风场,绿色/粉色/蓝色实线代表飞行航迹。
复合翼螺旋机动增程航迹的纵向与横航向跟踪误差Y=[ηe,ηlon,ηlat],如图16所示。可知,下降风与上突风增大纵向的跟踪误差,不连续的曲率切换引起纵向与横侧向跟踪误差突变,如圆弧段Ps→P1至直线段P1→P2引起纵向下滑角的突变,S-Turn转弯P2→P3→Pe引起横侧曲率突变。纵向跟踪误差限制在ηlon∈[-1°,1°],横侧向跟踪误差限制在ηlat∈[-1°,1.5°]。可知,在不同方向的风扰动下,其皆能抵抗风扰动并能精准跟踪参考航迹。当复合翼在从跟踪圆弧航迹到直线段航迹以及做S-Turn机动转弯时曲率不连续,由于预测模型具备对参考航迹曲率的预测能力,亦能保证精准跟踪性能。

图16 螺旋机动增程航迹跟踪误差
为验证制导算法在变环境下的鲁棒性,现比较NMPC与PID算法在不同强度的变向风场下的航迹跟踪性能,如图17所示。绿色箭头代表矢量风场,黑色虚实线代表参考航迹,蓝色实线代表PID算法下的飞行航迹,红色实线代表NMPC算法下的飞行航迹。阵风场强度分别为强风(六级)ω=10 m/s以及疾风(七级)ω=15 m/s;风向由东→北→南→西依次转变。如图17所示,随着侧风强度不断增强复合翼出现明显的追风效应,但2种制导算法具有一定的抵御风扰能力。在应对图17(a)强风以及图17(b)疾风时,NMPC算法对侧向误差与垂直误差的控制精度强于PID算法。仿真结果表明,当存在风扰动的情况下,所提制导方法可提高系统的跟踪精度,适合用于复合翼应急迫降的制导过程。事实上,为应对持续稳定的强风扰动,在规划中将风场信息引入到航迹中更为合理,如文献[3]所提应对任意常值强风场下的Trochoid航迹规划算法。
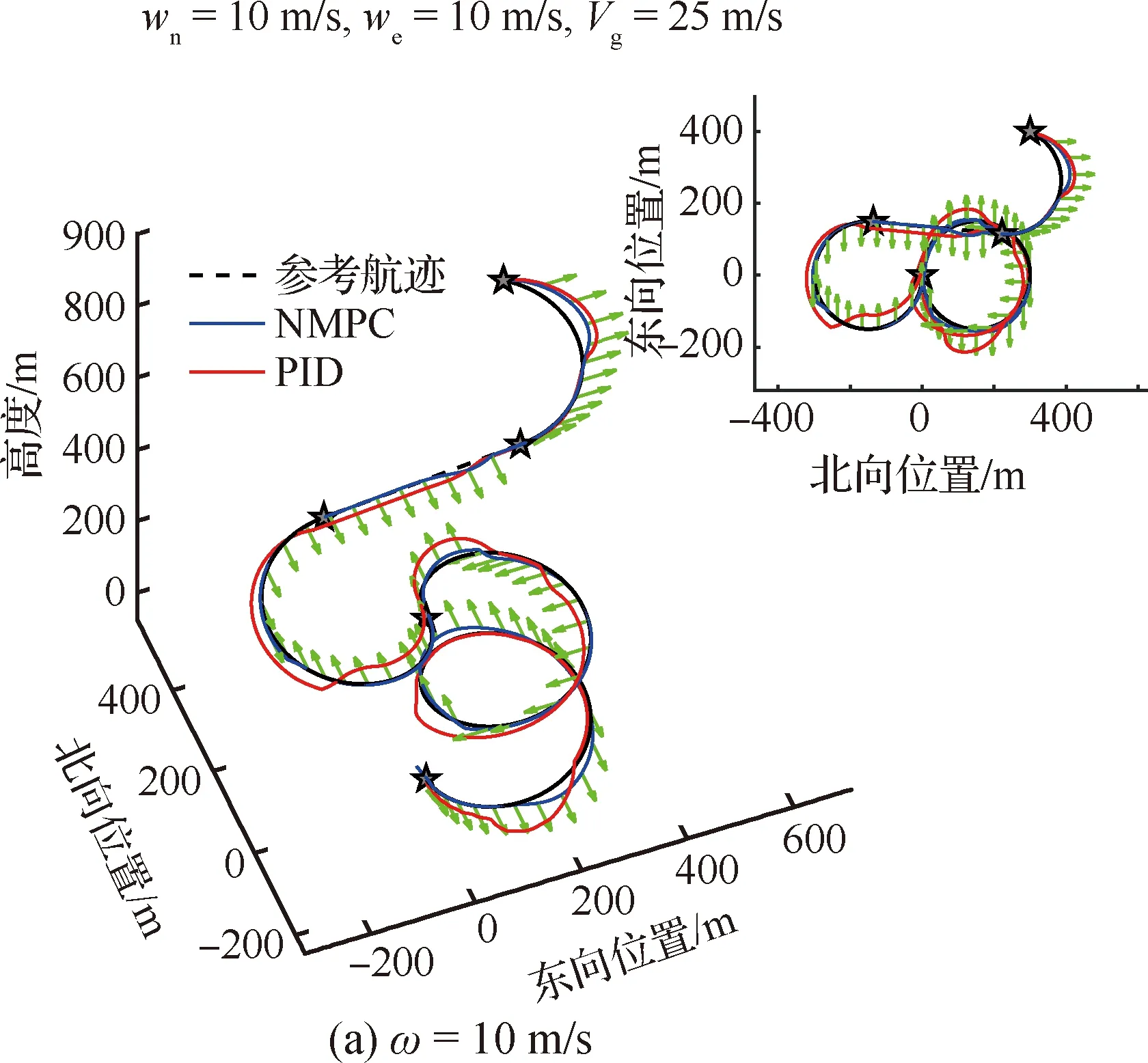

图17 不同强度的变向风场下NMPC与PID算法的航迹跟踪对比
5 结 论
针对混合动力复合翼飞行器空中停车后存在高度、横向位置、航向的不确定散布,终端约束,飞行总能量有限等特性,设计了相应的在线航迹规划方法及三维制导律。同时对在线航迹规划方法进行了在不同返场情况下的适应性仿真验证;对非线性模型预测控制制导算法进行抗风性仿真验证。通过研究得到如下结论:
1) 复合翼速度包线窄、初始能量状态散布小且对模型参数不敏感,其纵向航迹剖面只需通过简单的下滑角限制即可约束下滑性能,保证其速度自然稳定。基于速度静稳定性理论的3D Dubins在线航迹规划算法通过将下滑航迹划分为标准下滑航迹、S-Turn机动转弯航迹、螺旋机动增程航迹解决了复合翼在高度、横向位置、航向不确定以及终端约束、动力学约束下的航迹在线规划问题。
2) 所设计的非线性模型预测制导算法将跟踪误差、外界风扰动、航迹曲率不连续等非线性因素通过系统输出约束建模,具备一定抵抗风扰、提高制导精度的优点。同时,横纵解耦的制导律嵌入模型预测框架中,以高频率的滚动时域优化方式,实现三维Dubins航迹精确跟踪。
本文提出的航迹规划与制导方法同样应用于在可达迫降域内的固定翼飞行器无动力应急返场实时航迹规划与精确制导。此外,半实物仿真验证所提规划算法具备毫秒级的实时航迹规划能力。

