匀速俯仰运动及角速率对横向喷流的影响
赖江,赵忠良,王晓冰,李浩,李玉平
中国空气动力研究与发展中心 高速空气动力研究所,绵阳 621000
空中目标快速机动性能不断提升对战术导弹的精确打击能力提出了更高的要求,快速响应直接力/气动力复合控制技术成为提高导弹机动性能的关键技术之一[1-3]。直接力通常由微型脉冲发动机、燃气发生器或尾部主发动机引流产生横向喷流提供。横向喷流直接控制姿态或轨道的力和力矩,同时可利用与自由来流之间相互干扰产生有利的附加控制力和力矩。对横向喷流干扰的研究始于20世纪50年代[3-9],以分析定常流场结构和参数影响规律为主[10-12]。随着作战环境和技术需求更加严苛,非定常问题已成为战斗机和导弹设计中必须直面的挑战,包括过失速机动过程中显著增强的非定常气动效应,气动力的强非线性、交叉耦合、时间相关性,运动参数及舵面偏度影响;大迎角非定常气动力难以准确获取;准定常假设气动模型不再适用等问题[13-15]。横向喷流干扰同样存在影响控制效率的非定常特性问题[16-19],包括:干扰流场激波系和涡系固有的不稳定性,脉冲发动机启动和关闭过程中流场的建立和消退带来的波动,以及机动飞行非定常绕流的影响。
目前国内外针对飞行器运动情况下横向喷流干扰的非定常特性研究文献较少,主要有:赵海洋等[20]就球锥圆柱组合体模拟的强迫俯仰振荡过程,Jabaraj等[18]以导弹标模为对象,对比了传统气动建模/RBD和CFD/RBD方法在模拟运动过程横向喷流控制中气动/运动耦合现象的区别。陈坚强等[21]模拟了舵面快速运动导致的非定常迟滞效应。李斌等[11]比较了不同数量横向喷流和单独舵偏控制下对导弹姿态角建立时间的影响。但这些研究主要是针对动态过程的运动参数和宏观现象来讨论控制效率问题,没有详细地分析动态过程基本干扰流场的特点和变化。
为研究导弹大迎角俯仰机动过程中的横向喷流干扰特性,本文采用数值模拟方法,通过将大迎角俯仰机动近似为匀速俯仰运动来获取俯仰运动对横向喷流干扰特性和控制效率的影响。
1 动态数值模拟方法
本文研究对象是后体超声速横向喷流姿态控制的导弹模型,横向喷流喷管位置和基本边界条件如图1所示。
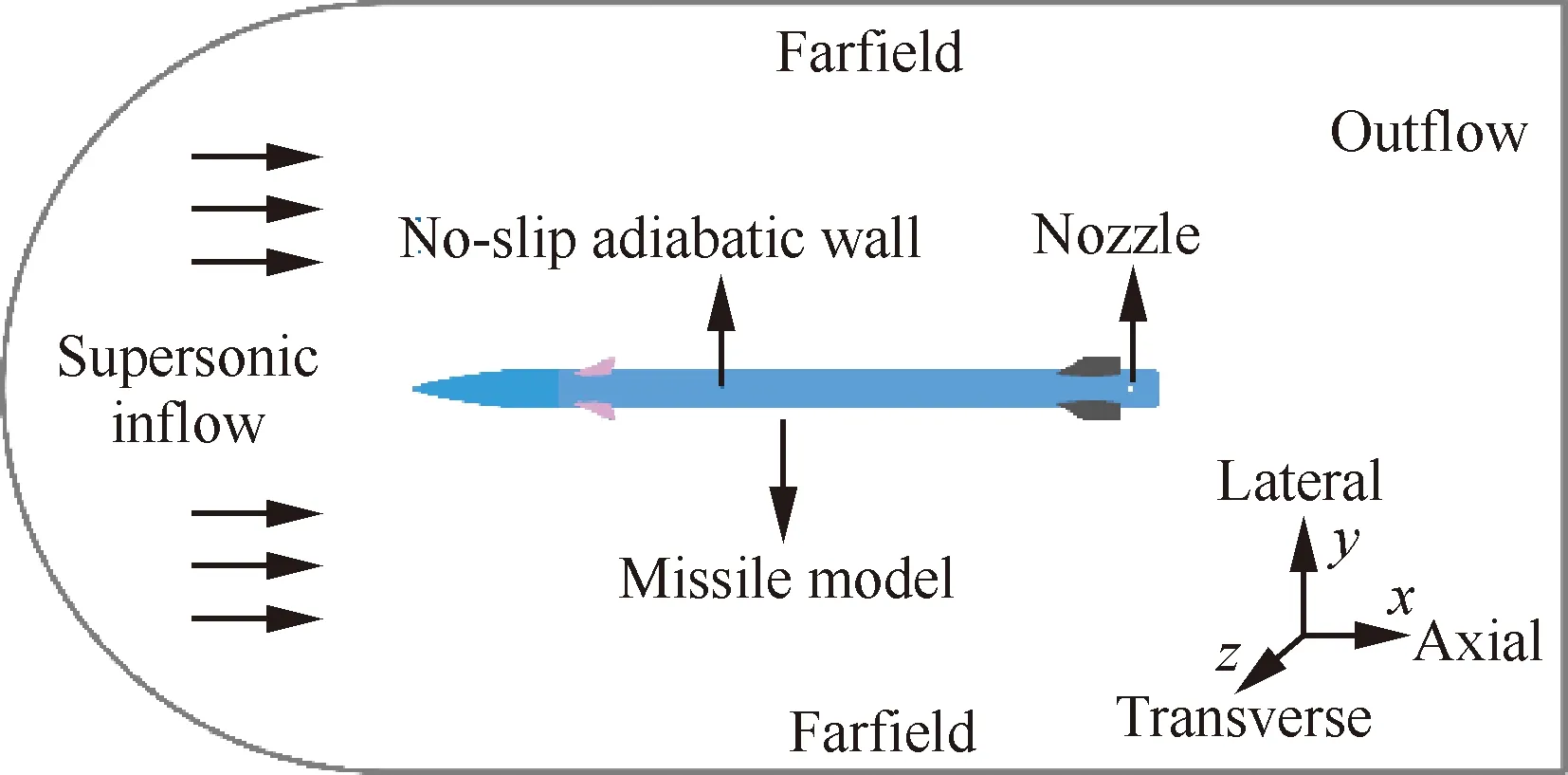
图1 计算模型、喷管位置和边界条件
求解一般曲线坐标系下的三维有黏可压缩流动控制方程,其无量纲形式为
(1)
式中:Q为守恒变量;(E,F,G)为无黏对流通量;(Ev,Fv,Gv)为黏性扩散通量;V为雅可比倒数;Re为雷诺数。
计算采用有限体积法,对流项为Van Leer分裂格式,黏性项为二阶中心差分格式,时间项为隐式LU-SGS方法。湍流模型采用Spalart-Allmaras单方程模型[22]。喷管入口边界条件设定为总压比(PR)和总温比(TR),其喷出方向为垂直于模型表面向外。计算基于多块对接结构网格,总量约1 000万。
动态非定常计算采用双时间步法,引入伪时间步,在指定匀速俯仰运动形式和参数下求解流动控制方程[23],首先用通量张量H(包括无黏项HI和黏性项HV)简化式(1),然后运用高斯定理针对任意区域对式(1)进行积分,并离散为
(2)
这里用Ri,j,k表示通过控制体的H净通量,包括了流入和流出网格单元两个部分。由于俯仰过程网格整体变化,未发生局部变形,因此动网格采用刚性旋转技术实现。式(2)写为
(3)
在此引入伪时间步τ,上标n表示真实时间步,非定常隐式计算格式为
(4)
用上标p表示伪时间步,W表示原始变量,离散后线性化的迭代式为
(5)
迭代方程中ΔQp→0则式(4)成立,时间满足二阶精度。
俯仰过程动态非定常计算的物理时间步长取为Δt=0.001 s,内迭代步数n=400。图2给出了一个物理时间步内的残差(红色线)和俯仰力矩系数Cm(蓝色线)收敛历程,气动系数几乎不变,内迭代残差下降了3个数量级,表明时间步长和内迭代步数满足计算要求。

图2 内迭代中残差和俯仰力矩系数收敛过程
2 俯仰运动对喷流干扰流场结构的影响
基于后体单独向上喷流模型,具体模拟条件和5种不同运动的典型对比参数见表1。以此获取的喷流干扰典型流场结构见图3。
图3(a)描绘了纵向对称面内喷口上游的分离激波和弓形激波、喷口上方的桶形激波和马赫盘、喷口上游激波边界层干扰出现的流动分离区以及喷口下游由导弹模型尾部收缩段引起的流动分离区。

表1 来流、喷流和运动条件
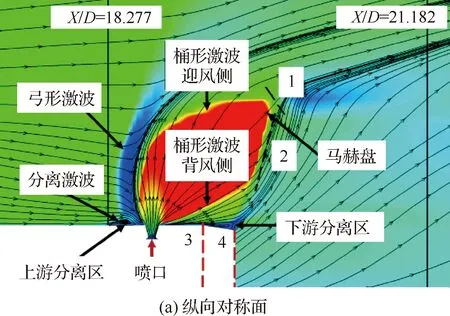
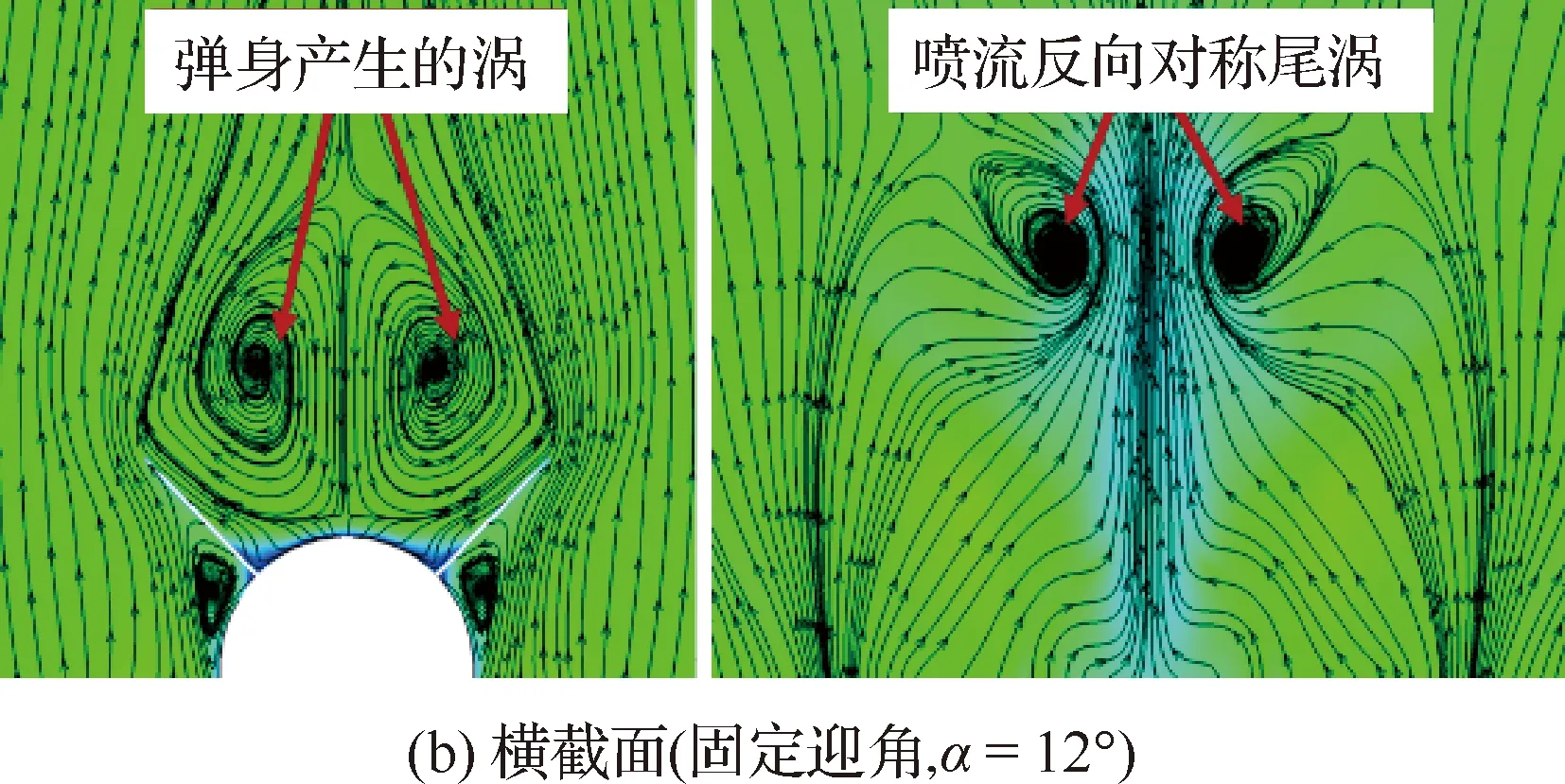
图3 典型横向喷流干扰流场结构
图3(b)是分别位于X/D=18.227(喷口上游分离起始点附近)和X/D=21.182(喷流尾部羽流后)两个横截面的涡结构,其中X表示从模型头部起始点到该点的距离,D表示等直段直径。弹身涡穿过喷流上游激波区时被破坏,在马赫盘后方出现一对远场反向对称喷流尾涡。
按干扰流场前、中、后部分进行分析,对比表1中列出的不同迎角、俯仰方向和角速率q运动过程对干扰流场的影响,结果如图4和图5所示。
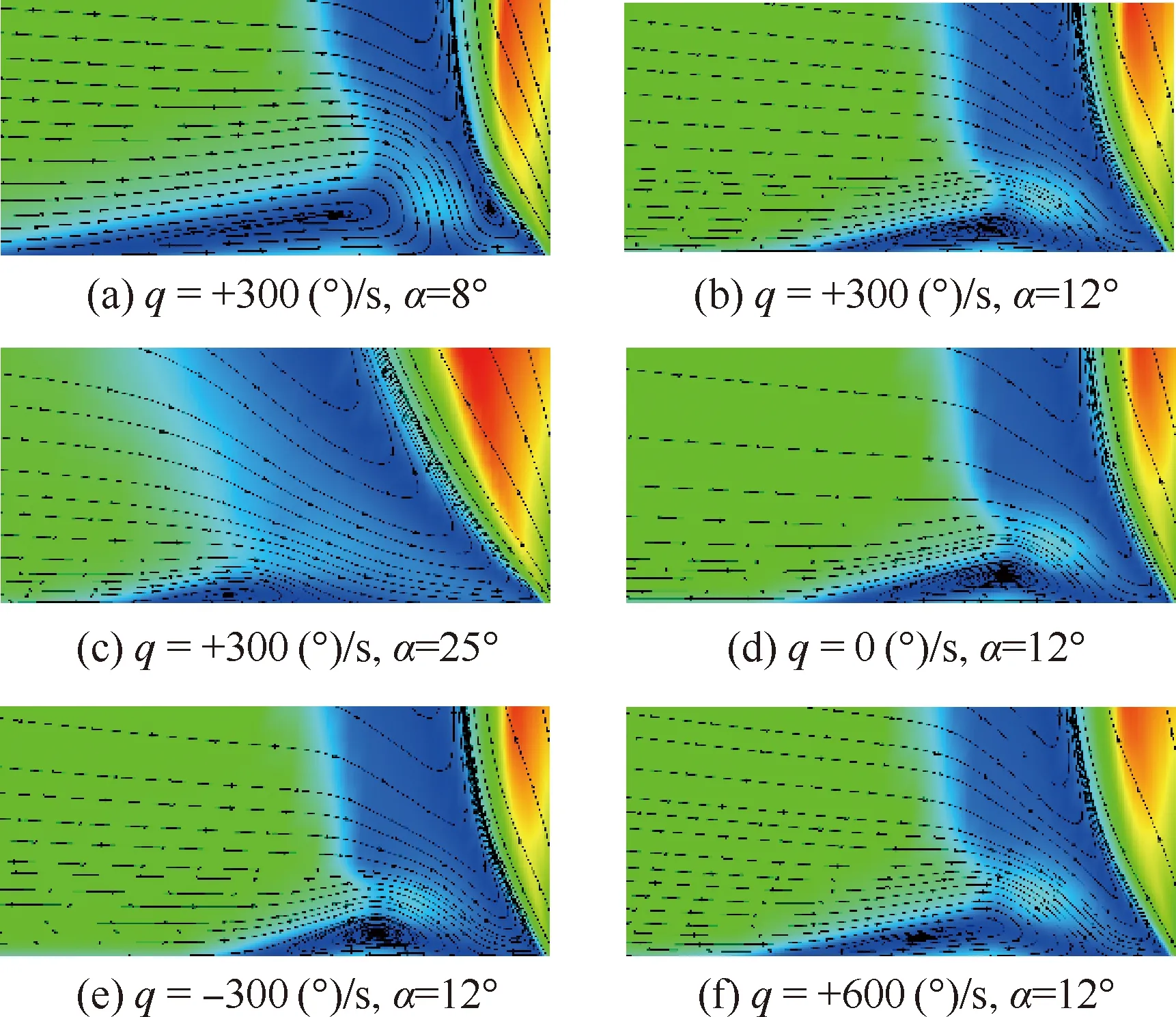
图4 运动对干扰流场前部的影响
2.1 上游分离和弓形激波
由图4(a)~图4(c)可见,随迎角增加,喷流上游分离区减小;分离激波位置逐渐靠近模型表面;弓形激波远离喷口;小迎角α=8°分离区内同时存在顺时针主分离涡和逆时针次分离涡,中等迎角α=12°主分离涡明显,大迎角α=25°分离弱。
表1中设定的喷流角度A,即来流与喷流方向夹角,固定迎角状态下约为90°。由图4(b)、图4(d)和图4(e)可见,相对于固定迎角状态,运动迅速改变模型姿态,喷流角度A稍减小为锐角,来流对喷流的阻挡效果减弱,导致弓形激波前移,其浸入边界层所产生的附着点位置相应提前。下俯过程A稍大于上俯过程,因此其来流角度更平缓,两者混合强度减弱,轴向分离区比上仰时小。这种局部分离现象不同于传统外流弹身涡的分离,上仰过程由于前序迎角附着,迎角增大但还来不及分离,导致分离减小。而对比图4(b)和图4(f)可见,更大的俯仰角速率加强了绕流非定常特性,上仰上游分离区略提前,弓形激波前移。
从前部来看,运动对中小迎角的改变在于分离区结构和强度,而大迎角下主要影响弓形激波位置,下俯影响比上仰影响更明显。
2.2 桶形激波和马赫盘
λ波结构使喷流偏转在喷口上方形成的桶形激波迎风侧和背风侧终止于马赫盘,即图3(a)中标志1。桶形激波穿过喷流,使喷口背风侧边缘的膨胀波在横穿桶形激波的同时向来流方向偏转,而标志2附近桶形激波边缘出现偏折现象。标志3和标志4是收缩段,后体横向喷流处于背风区,尾部气流膨胀效应使桶形激波背风侧超出模型尾部,需调整激波倾角,增加激波强度,以适应膨胀导致的压力减小。这种偏折效应在中小迎角下较明显,但大迎角时超出尾部部分随桶形激波偏转减小而减少,偏折现象减弱,马赫盘更明显。
图5展示了运动影响下干扰流场中部的结构特征,图中条件与图4一致。由图5(a)~图5(c)可知,迎角增加导致喷流夹角A=90°的正面冲击减小,即来流与背风面喷流接触时碰撞的刚度相对削弱,桶形激波面积得以扩大,马赫盘位置上移,两者混合后的偏转程度减小。
相对于固定迎角状态,上仰使桶形激波面积减小,下俯使之增加;迎风面受运动影响较小,背风侧上仰激波倾角增大,偏折增强,马赫盘前移,尾部偏折效应增强;而下俯激波倾角减小,背风侧离开物面位置较远,偏折效应减弱。绕流流动特征被俯仰角速率的增大放大,引起上仰背风面更加靠近物面,以致更明显的偏折影响。
从中部来看,运动及其角速率主要影响桶形激波背风面偏转程度和尾部偏折效应。
2.3 下游分离和收缩段分离激波
高度欠膨胀喷流射出后冲破由压力差造成的压缩现象,逐渐调整并融入环境压力。下游的分离来自两个方面:一是喷流膨胀后在喷口下游近壁面造成的分离;二是模型尾部收缩构型诱导的下游气流分离。分离区外边界出现激波以调整速度和压力。由图5可知,随迎角增加,下游分离区位置提前;中等迎角的分离激波较明显;由于桶形激波背风面激波倾角变大,波后压力增加,进而减弱分离激波强度。
相对于固定迎角,上仰使下游分离区变大,分离激波向桶形激波偏转,而来流平缓的下俯过程混合作用稍弱,抑制流动分离,分离激波向物面靠近。俯仰角速率增大仅加强运动影响的程度,偏折效应也增强。
整体来看,运动对横向喷流干扰的影响主要体现在:中小迎角下上游分离涡、桶形激波范围及其背风侧下游的偏折现象;而大迎角下弓形激波位置改变较大。
3 俯仰运动对压力分布和极限流线的影响
第2节描述的现象也能通过表面极限流线反映。图6给出了典型分离拓扑细节。包括喷口上游高压区和下游低压区共同形成的压力平台效应。
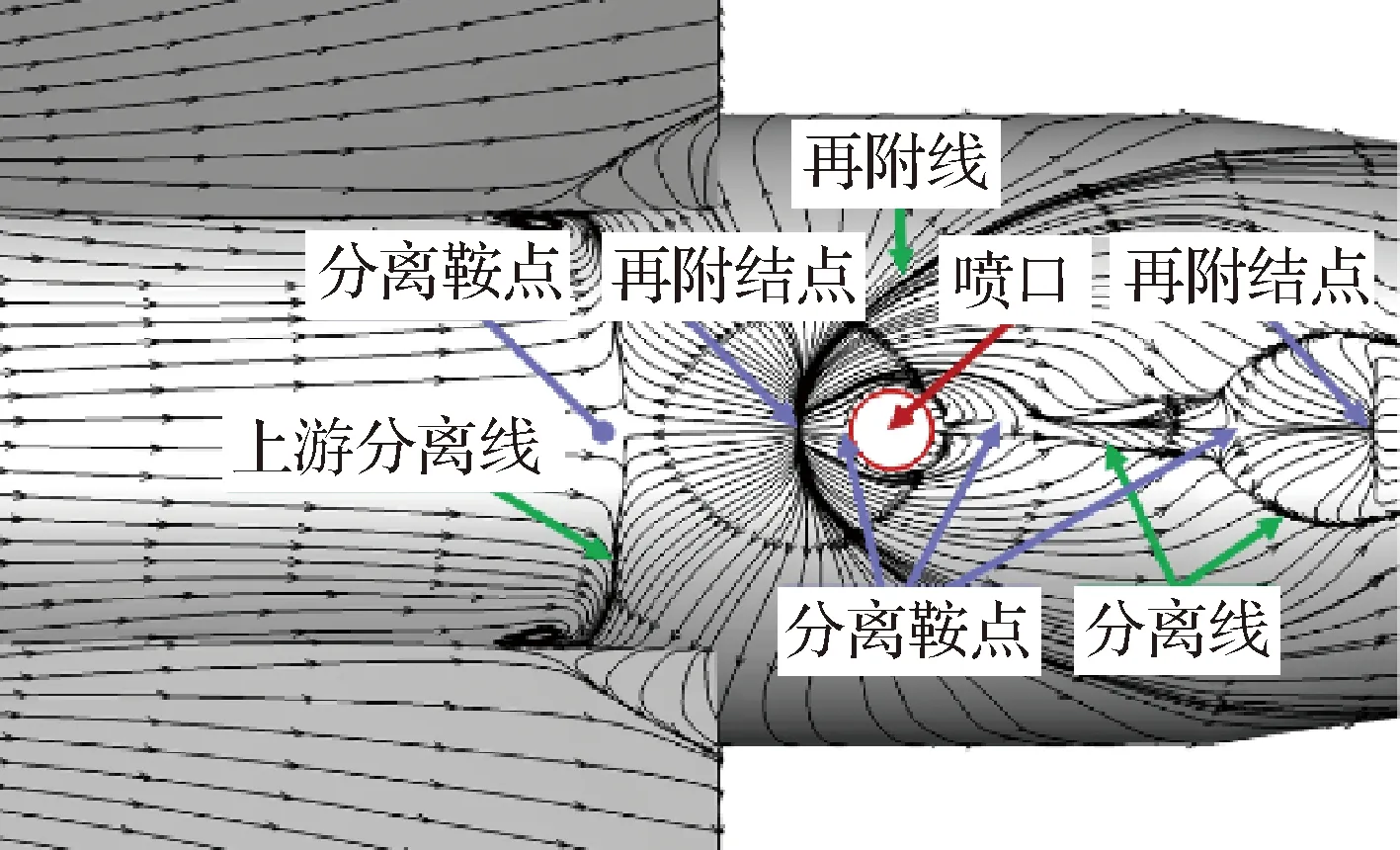
图6 喷口附近模型表面极限流线
3.1 压力平台效应和表面极限流线
图7为后体压力系数Cp分布云图和表面极限流线。迎角增加导致相互作用程度减弱引起更充分的喷流膨胀,因此下游低压区范围扩大,大迎角下弓形激波向上游推进明显,导致分离区减弱,高压区强度减弱,分离再附线严重变形。
由于正迎角时模型阻挡来流,减弱了对后体喷流的冲击,致其扩散范围更广,但运动增强的非定常扰动在上仰时尤其明显,而下俯由于喷流角度A较上仰稍大,来流角度相对减小又降低了混合强度。因此,相对于固定迎角,下俯时上游高压区增大并靠近喷口,上游分离线推后,下游分离更复杂多样。
表2列出了上游分离起始点位置,该临界点在纵向对称面上,通过极限流线提取。所有状态中上仰α=4°最先分离,下俯α=16°最后分离,表明下俯抑制分离。此外关注图7中靠近喷口的尾舵,干扰流场上游高压区增大了尾舵压力。中小迎角下迎角增加或下俯都导致高压影响区减小;大迎角下由弓形激波前移引起该区域扩大,甚至涉及整个舵面展向。由图7(b)和图7(f)可知角速率增加导致高压影响区扩大。
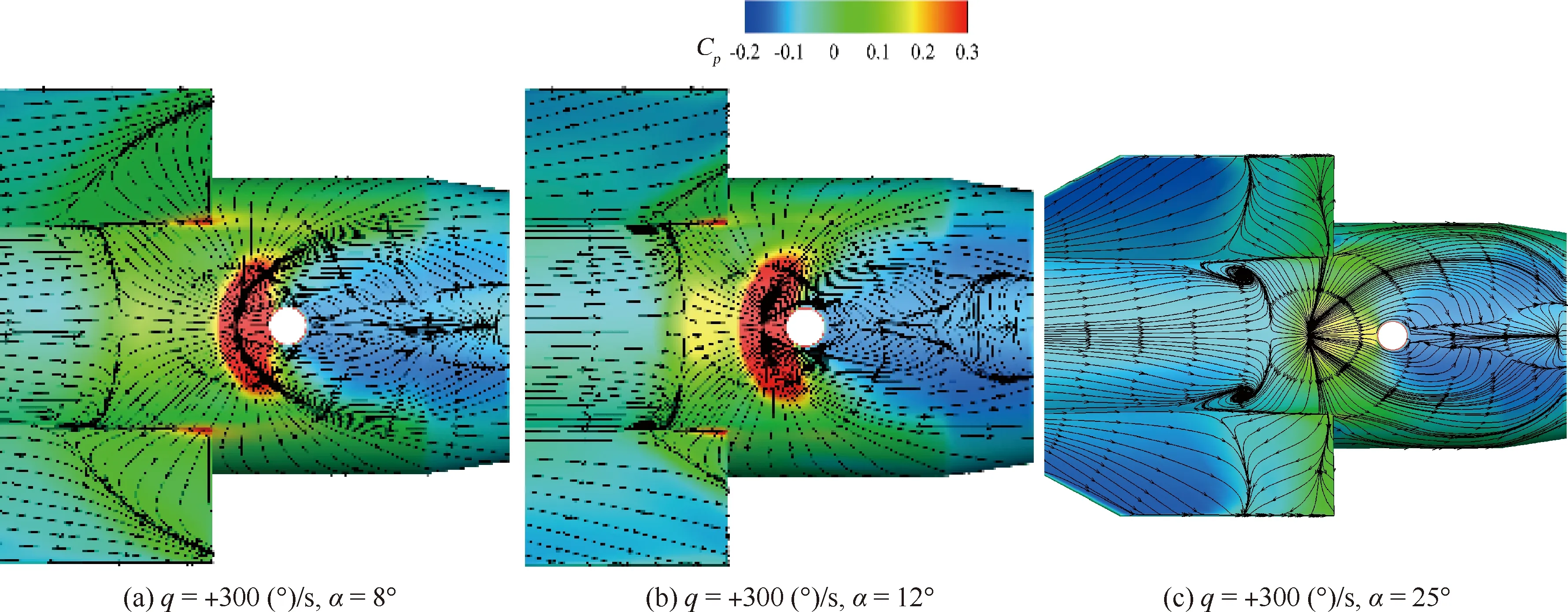

图7 喷口附近模型表面压力系数对比

表2 上游分离起始点位置
3.2 表面子午线压力系数变化量分布
获取以上流场特征后进一步开展压力变化定量评估。图8为上仰Φ=0°子午线压力变化量ΔCp分布。以中等迎角α=12°为界,α<12°上仰压力系数变化量峰值ΔCpmax较下俯减小,上游分离区变大,α>12°则相反。运动对下游低压区ΔCp影响趋势一致,但下俯使ΔCp绝对值更大。
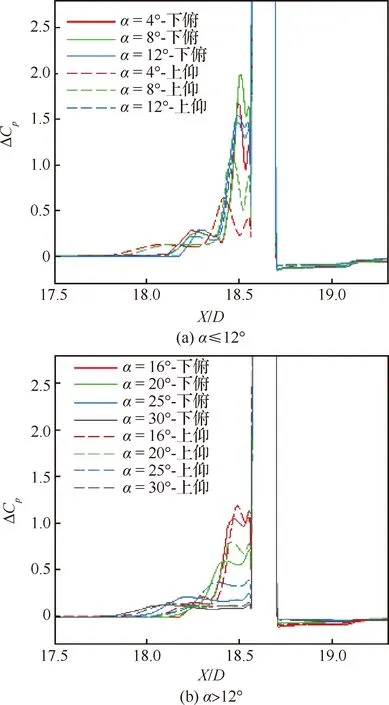
图8 不同迎角模型表面子午线压力系数变化量分布(q=+300 (°)/s)
图9为不同角速率及上仰过程上游ΔCpmax和下游ΔCpmin在运动中随迎角的变化趋势。图9(a)中极值均出现于α=8°。图9(b)~图9(d)中运动致α<12°上游分离区增加,上仰使上游ΔCpmax减小,下俯使其增加;角速率增大引起上仰ΔCpmax减小,分离区增加,下俯变化相反。α>12°情况基本与此相反,上仰ΔCpmax随迎角增加逐渐接近固定迎角值。俯仰角速率对下游低压区ΔCp影响较弱,随角速率增加而减小。
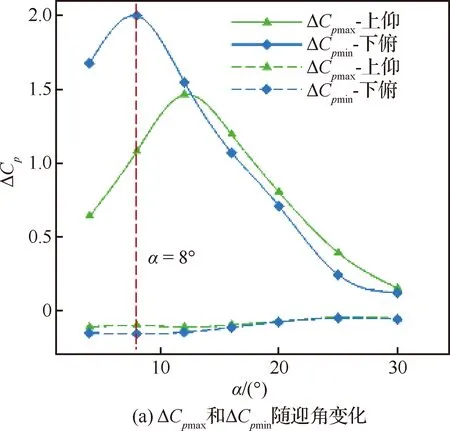
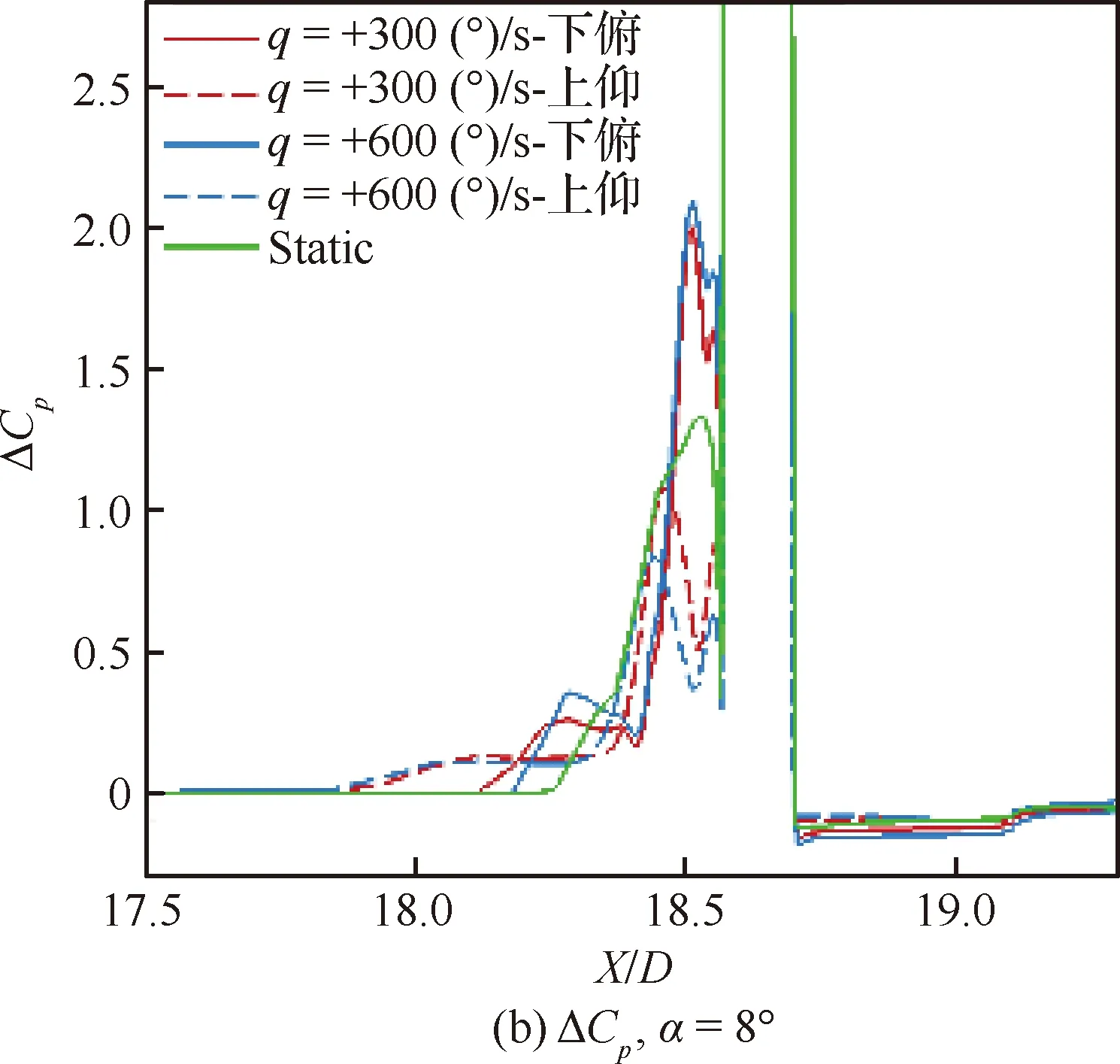
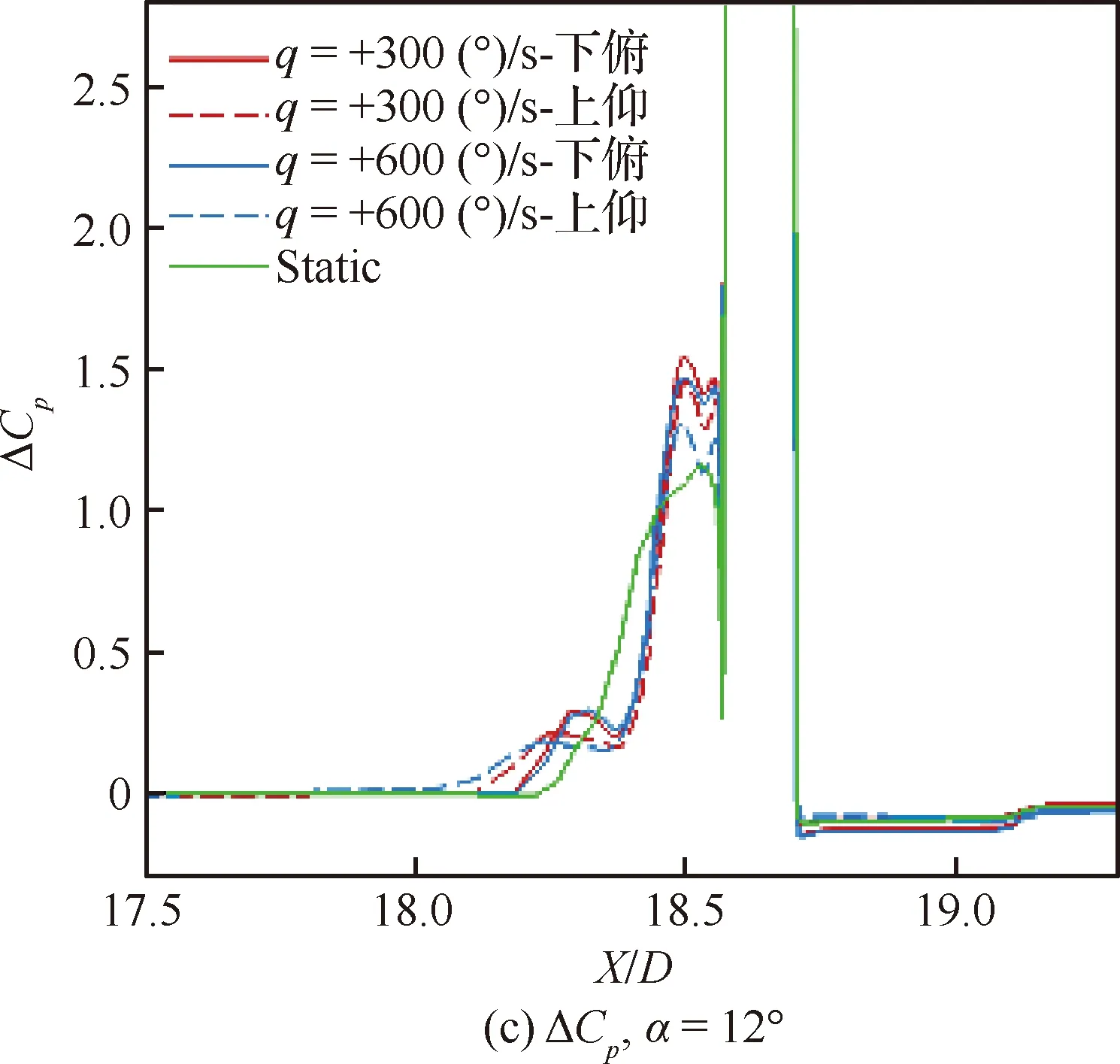
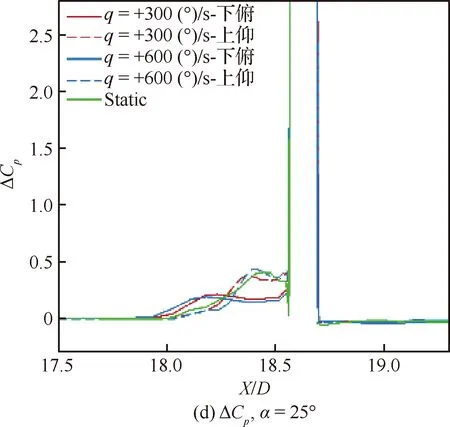
图9 俯仰角速率对子午线压力系数变化量分布影响
4 俯仰运动对气动特性及干扰评估的影响
4.1 动态迟滞特性
基于以上定性和定量的分析,图10对比了静/动态俯仰气动特性。由于绕流场中涡随模型运动变化,气动系数存在动态迟滞,细长体法向力系数CN迟滞较弱。相对静态,上仰模型背风侧涡离物面更近,表面压力减小,压心靠后,导致俯仰气动系数绝对值增加;下俯过程与之相反。模型周围涡主导的绕流场可用的调整时间随角速率增加而缩短,迟滞现象更加明显。
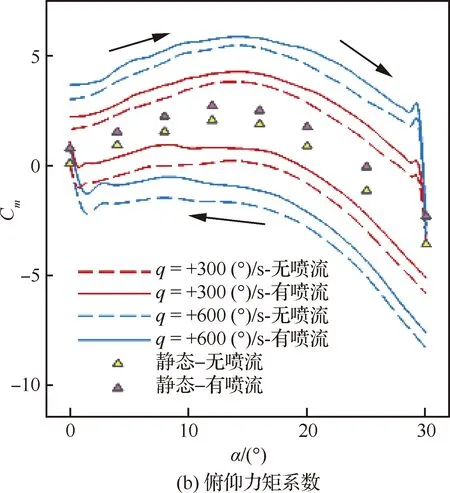
图10 静/动态气动特性对比
4.2 动态力和力矩干扰特性
图11对比了气动系数干扰量在运动过程中的变化,为了对比两种不同角速率达到相同迎角的变化过程,图中上边界表示以+600(°)/s的俯仰角速率(蓝色线)运动的时间,下边界表示以+300(°)/s的俯仰角速率(红色线)运动的时间。中小迎角时ΔCN比大迎角时大。大迎角运动导致ΔCm减小。不同角速率变化趋势一致,主要影响在上仰中小迎角和下俯过程。
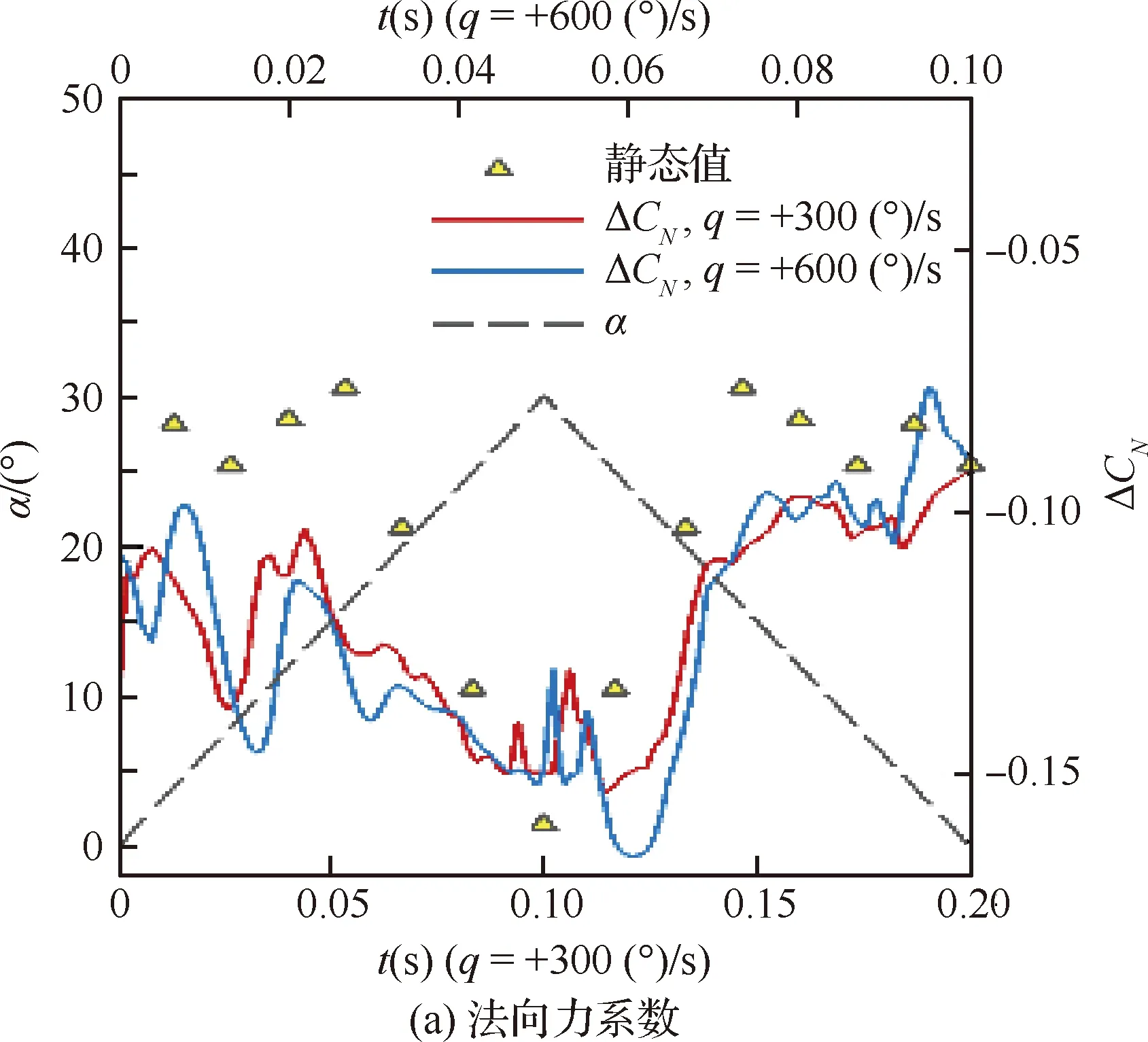
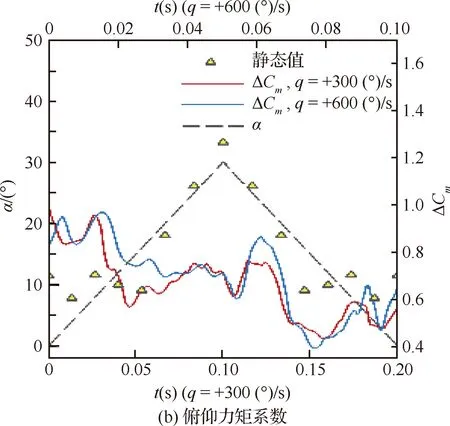
图11 迎角和力矩干扰量随时间变化曲线
4.3 动态喷流干扰放大因子
横向喷流干扰程度评估参数[17]为干扰力放大因子KF和力矩放大因子KM。图12为5种状态对比,单独喷流推力根据公式估算[11]。KF动态值普遍大于静态值。在α<20°范围内,KM受运动影响大,上仰值大于静态值,下俯值则变小;大迎角下KM动态值明显小于静态值,且出现多个迟滞环。放大因子在上仰中等迎角和下俯大迎角过程随角速率增加而增大。
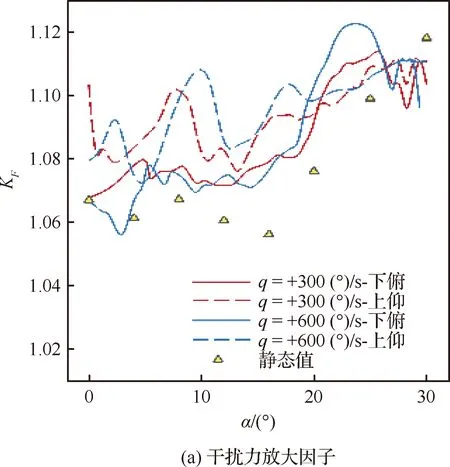
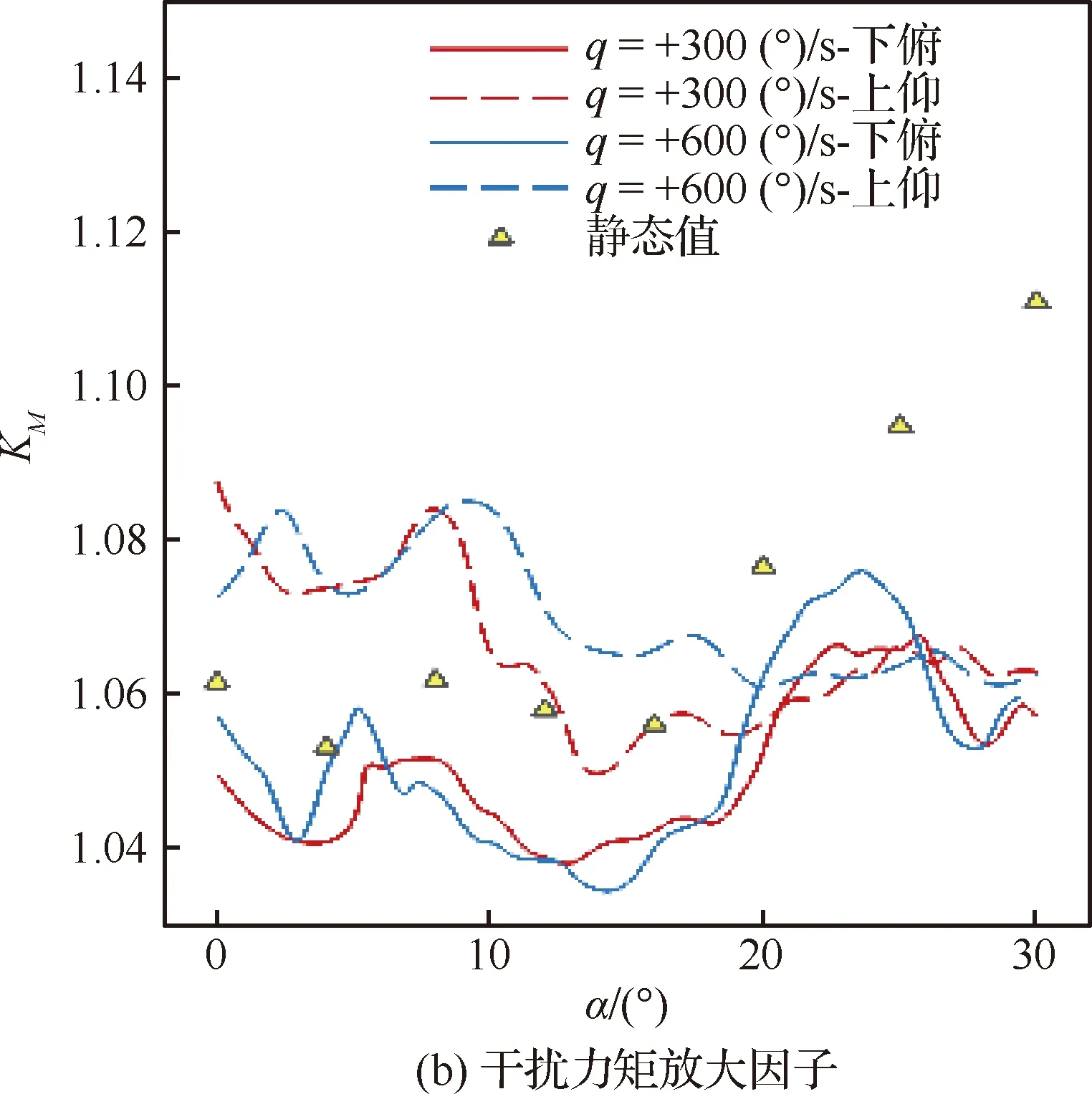
图12 横向喷流干扰放大因子
5 结 论
通过VFNS(Virtual Flight Navier-Stokes Solver)求解器进行数值模拟,对比分析了横向喷流干扰下,导弹模型固定迎角、不同俯仰角速率匀速俯仰运动5种状态下,喷口附近干扰流场结构受到的动态影响,最终评估了其气动特性和干扰放大程度。
1) 俯仰运动及其角速率显著改变桶形激波背风面偏转程度和尾部偏折效应角度。
2) 中小迎角下,俯仰运动主要影响喷口上游分离区,而大迎角下主要影响弓形激波位置;俯仰角速率增加导致上游分离提前。上仰和下俯对喷口上游高压区影响相反,且下俯影响更显著,下俯过程还抑制了下游分离。
3) 中小迎角增加或下俯过程使喷流干扰形成的尾舵高压区缩小,但大迎角下该区域甚至扩大至整个舵面展向。
4) 俯仰运动的气动特性出现动态迟滞,角速率增加导致迟滞增强。运动对KM影响较大,在大迎角时显著减小。

