SV波斜入射下河谷地形地震动分布特征分析

孙纬宇， 汪精河， 严松宏， 欧尔峰， 梁庆国

(1. 兰州交通大学 土木工程学院，兰州 730070； 2. 兰州交通大学 甘肃省道路桥梁与地下工程重点实验室，兰州 730070；3. 甘肃省轨道交通力学应用工程实验室，兰州 730070)

大量震害调查和强震监测表明，局部地形对地面运动的影响很大，发现突出的山梁、河谷、陡崖陡坡等不规则地形上的震害较平坦场地更为严重[1-4]。不规则地形下入射波散射效应对场地地震响应的影响，主要由入射波频率、入射角度、地形几何形状、介质性质等几个因素所制约[5]。对于深源地震，可认为地震波是垂直入射的，此时入射波的输入是一简单的一维问题，当震源距离场地较近时，地震波并非垂直向上入射，而是以一定的角度倾斜入射。随着跨河谷工程的大量涌现，河谷场地的地震动响应成为了地震工程领域研究的热点，为了全面了解河谷地形对地震动力响应的影响规律，确保重大跨河谷工程在地震作用下的安全性，有必要对地震波斜入射下河谷地形的动力响应规律进行研究。

目前对于河谷地形地震动响应的研究方法主要有解析法和数值法。解析法适用于较规则的半圆或半椭圆地形，如P波[6-7]、SH波[8-9]、SV波[10-11]入射下半圆形沉积河谷的动力响应等；数值法由于不受地形条件的限制，应用更为广泛。周国良等[12]研究了SV波入射下河谷地形地震动的分布特征；丁海平等[13]研究了P，SV波斜入射下凹陷地形的地震动分布特征；陈少林等[14]研究了半圆柱型沉积盆地对SH波的散射问题；车伟等[15]研究了典型山谷地形桥址对地震波传播的影响。

本文基于黏弹性边界的等效荷载输入方法，在大型通用有限元软件ANSYS上实现了SV波的斜入射。以典型河谷地形为研究对象，分析了SV波入射角度和河谷斜坡坡度对河谷场地地震动分布特征的影响。

1 地震波斜入射输入方法

1.1 黏弹性人工边界

在模拟半无限地基时，必须设置合适的人工边界条件来模拟无限域介质带来的影响，黏弹性边界由于很好地模拟了半无限地基的辐射阻尼和弹性恢复能力，得到了广泛的使用[16]。在ANSYS中，黏弹性边界可采用combine14弹簧单元来模拟，其弹簧的刚度和阻尼参数按下式计算：

(1)

式中:Kn和Kt分别为弹簧的法向和切向刚度系数，Cn和Ct分别为法向和切向阻尼系数，G为剪切模量，ρ为密度，Cp和Cs分别为压缩波速和剪切波速，R为散射波源到人工边界的距离，一般取几何中心到每个边界距离的平均值。

1.2 人工边界上的等效节点力

假设地震波是以α角入射的平面SV波，如图1所示，此时需在左侧人工边界和底边人工边界上施加等效节点荷载[17]。

图1 二维平面SV波斜入射示意图Fig.1 Two-dimensional diagram of plane SV-wave oblique incidence

对于左侧边界：

(2)

对于底边界：

(3)

式(2)～(3)中：Ab为人工边界上节点b所影响的面积，与时间有关变量的上标代表节点所在人工边界的外法线分量，下标代表节点号和分量方向，与坐标轴方向一致为正，相反为负。

1.3 位移场求解

根据局部波场分解方法[18]，对于人工边界的某一局部，将总波场分解为内行场和外行场，内行场是指从无限域通过人工边界进入有限域的波场，假设无限域为弹性介质，可对各种波进行叠加计算。相反，从有限域通过人工边界进入无限域的称作外行场，其由人工边界提供，无需另外计算。

对于左侧人工边界，内行场由入射角为α的SV波，反射角为α的SV波和反射角为β的P波组成，位移场为：

(4)

式中：A1为反射SV波与入射SV波幅值比，A2为反射P波与入射SV波幅值比，由下式计算：

(5)

对于底边界，内行场仅有入射SV波，位移场为：

(6)

式(4)和(6)中：Δt1～Δt4分别为波传播到左边和底边人工边界节点所需时间延迟，可通过传播距离除以波速得到。对于右边界，只有外行场而无内行场，不需要计算。

1.4 应力场求解

对于左侧边界，应力场由入射SV波、反射SV波和反射P波叠加而成：

(7)

对于底边界，仅有入射SV波产生的应力：

(8)

式(7)～(8)中：λ为拉梅常数，G为动剪切模量。

同样，右侧边界也无应力输入。将式(4)～(8)及求导后的速度场表达式代入式(2)～(3)中，可以得到人工边界上的等效节点力表达式。

垂直入射时，三边都需施加相应的等效节点力，此时只有反射SV波，无反射P波，将α=0°代入上述公式，可得左边和底边等效节点力表达式，而右边等效结点荷载由对称性可得：

(9)

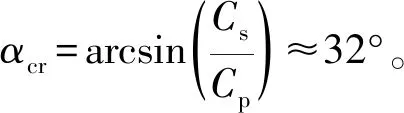
在ANSYS中，通过APDL编程实现了粘弹性边界的自动施加，并按照上述解析方法，编制了基于波动理论的地震动输入程序，在ANSYS中完成了地震动的波动输入方法。

2 方法验证

假定一均匀弹性半空间模型如图2所示。模型尺寸和计算参数分别为：长1 600 m，高400 m，介质密度ρ=2 000 kg/m3，弹性模量E=1.25 GPa，泊松比μ=0.25，Cs=500 m/s，Cp=866 m/s，单元尺寸为Δx=Δy=10 m。

在模型表面中部设置监测点A。

图2 弹性半空间有限元模型Fig.2 Finite element model of elastic half-space

入射波的入射角α=15°，位移时程如图3所示，峰值为1 m。通过编制的程序，可将位移时程和速度时程转换为节点力施加在模型边界上。其计算结果如图4和图5所示。

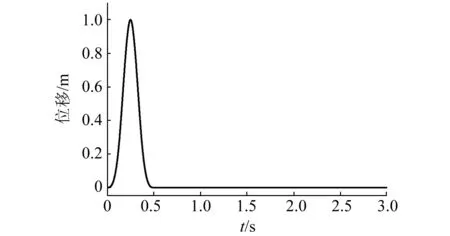
图3 入射波位移时程Fig.3 Displacement-time history of incident wave

图4 SV波15°斜入射时半空间位移场云图Fig.4 Displacement contour of the semi-infinite space under SV waves with 15° incident angle

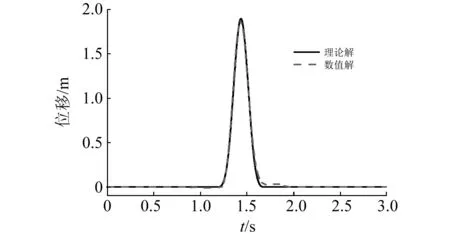
图5 监测点处的位移时程曲线Fig.5 Displacement time history at observation point

从图4中可以清楚的看到SV波以一倾斜波阵面进入有限区域，经地表反射产生的反射P波和反射SV波，及其在半空间的叠加情况。从图5中可以看到，均匀弹性半空间的数值解与理论解吻合的很好，说明了本文SV波输入方法和程序的正确性。

3 河谷场地计算模型及参数

假定该河谷场地为均质、各向同性的弹性体，密度ρ=2 000 kg/m3，泊松比μ=0.25，剪切波速Cs=392 m/s，Cp=734 m。模型总宽度为560 m，总高度为160 m，河谷底部宽度为60 m，两侧坡高均为60 m。在河谷地形表面布置监测点，在距离坡顶较远处每隔20 m布置一个监测点，在坡顶附近、坡面以及河谷底部每隔10 m布置一个监测点。河谷地形模型和监测点布置如图6所示。

坡角θ分别取为45°、60°、75°和90°，地震波的入射角度α分别为0°、15°和30°，从模型的左侧入射。选取的地震波分别为El-Centro波、宁河波和Northridge波，幅值均调整为0.2 g，其加速度时程如图7所示。

图6 河谷地形模型及测点布置示意图Fig.6 Valley topography model and observers position layout

图7 加速度时程曲线Fig.7 Time history of acceleration

3 河谷场地地震动响应分析

定义地震动放大系数为河谷表层观测点的加速度峰值Amax与入射波加速度峰值Amax,input的比值[4]，用β来表示，即β=|Amax/Amax,input|。

3.1 坡度和入射角度对河谷地表地震动的影响

提取了不同入射角度和斜坡坡度时河谷场地地表监测点的地震动放大系数，其变化规律如图8～10所示。

从图8～图10可以看出，河谷斜坡坡度对河谷场地地震动放大系数的分布有较大影响。随着河谷斜坡坡度的增大，以不同角度入射时河谷斜坡坡面以及坡顶上一定范围内的地震动放大系数显著增大。当地震波以垂直方向(0°)入射时，河谷两岸地震动放大系数的x分量和z分量均呈对称状分布，且x向分量显著大于z向分量；当地震波以15°和30°的角度倾斜入射时，河谷两岸x向分量和z向分量地震动放大系数均呈不对称分布，且随着入射角度的增大，这种不对称现象越明显；对于x向分量，河谷左岸的地震动放大系数明显大于右岸地震动放大系数，且随着入射角度的增大，左

图8 El-Centro波以不同角度入射时各斜坡坡度下各测点的地震动放大系数Fig.8 Amplification coefficient of monitoring points at different angles under different slopes of the El-Centro wave.

图9 宁河波以不同角度入射时各斜坡坡度下各测点的地震动放大系数Fig.9 Amplification coefficient of monitoring points at different angles under different slopes of the Ninghe wave

图10 Northridge波以不同角度入射时各斜坡坡度下各测点的地震动放大系数Fig.10 Amplification coefficient of monitoring points at different angles under different slopes of the Northridge wave

岸的地震动放大效应增强，右岸的放大效应在减弱；对于z分量，河谷右岸的地震动放大系数要大于左岸的地震动放大系数。总体上，河谷左岸(地震波入射侧)的x向分量的地震动放大效应占据了主导地位，且入射角度越大，这种放大效应越明显，在河谷场地的抗震设防中要重点考虑。

3.2 坡度和入射角度对坡顶地震动放大系数的影响

提取了地震波以不同角度入射时各斜坡坡度下坡顶处的地震动放大系数，由于河谷左岸x向分量占主导地位，因此只分析左岸坡顶的地震动放大系数。其变化规律如图11所示。

从图11可以看出，以不同角度入射时坡顶处地震动放大系数随坡度的增大均呈线性增长趋势，其R2(相关系数的平方)的最小值为0.9533，表现出了较强的线性关系。当各地震波以0°和15°角入射时，坡顶处地震动放大系数随坡度的变化速率基本一致，拟合曲线斜率以El-Centro波入射时相差最小，为0.0001，以Northridge波入射时相差最大，为0.0031。当地震波以30°角度入射时，坡顶地震动放大系数随坡度的增大增长较明显，拟合曲线斜率的变化范围为0.0175～0.0275。因此，地震波以不同角度入射不同坡度的河谷地形时，坡顶处的地震动放大系数可以用线性函数βi=kθ+b来进行估算，其斜率k主要受坡度的影响，截距b主要受入射角度的影响，入射角度越大，截距b就越大。

3.3 坡度和入射角度对坡顶影响宽度的分析

由波动理论可知，弹性介质中地震波在地表处发生反射，地表处地震动幅值为入射波幅值的2倍[18]。受斜坡坡度及入射角度的影响，河谷表面地震动放大系数分布规律较为复杂，其对坡顶平台的影响宽度也不相同。以垂直入射时均质弹性半无限空间地表地震动放大系数的理论解2.0作为参考值，从坡顶至平台上地震动放大系数大于2的区域可认为是河谷斜坡的影响宽度(图6中的Li)。图12给出了地震波以不同入射角度入射时斜坡坡度与坡顶影响宽度的关系。

注：图中θ表示河谷斜坡坡度，分别取45°、60°、75°和90°；βi表示坡顶加速度放大系数，i表示地震波入射角度，分别取0°、15°和30°。 图11 入射角度和斜坡坡度对坡顶地震动放大系数的影响Fig.11 Effect of incident angle and slope angle on the amplification coefficient of slope crest

注：图中θ表示河谷斜坡坡度，分别取45°、60°、75°和90°；Li表示坡顶影响范围，i表示地震波入射角度，分别取0°、15°和30°。 图12 不同入射角度和斜坡坡度时坡顶平台的影响宽度Fig.12 Effect width of slope top platform under different incident angle and slope angle

从图12中可以看出，各地震波以不同角度入射时，坡顶平台的影响宽度随斜坡坡度的增大基本呈线性增大趋势，但其线性趋势没有坡顶地震动放大系数随坡度变化时的线性好，R2在0.7248～0.9887之间。入射角度和斜坡坡度越大，坡顶平台的影响宽度也越大。当地震波垂直(0°)入射时，坡顶平台的影响宽度为0.13 H～1.83 H；当地震波以15°入射时，坡顶平台的影响宽度为0.92 H～2.30 H；当地震波以30°入射时，坡顶平台的影响宽度为1.5 H～2.72 H。其中，当入射角度和斜坡坡度均达到最大时，坡顶影响宽度也达到了最大。因此，在河谷平台上修建建筑物时，要充分考虑河谷斜坡坡度和地震波入射角度的影响，留出充足的安全距离。

3.4 坡度和入射角度对坡顶反应谱的影响

计算了地震波以0°、15°和30°入射、河谷斜坡坡度为45°、60°、75°和90°时坡顶处的反应谱。由于x向分量大于z向分量，因此，只分析了x向分量。以0°入射不同坡度的河谷来分析坡度对坡顶反应谱的影响，如图13所示。以45°斜坡的河谷来分析地震动入射方向对坡顶反应谱的影响，如图14所示。

图13 0°入射不同斜坡坡度坡顶加速度反应谱Fig.13 Acceleration response spectra of slope crest in different slope angles under incident angle 0°

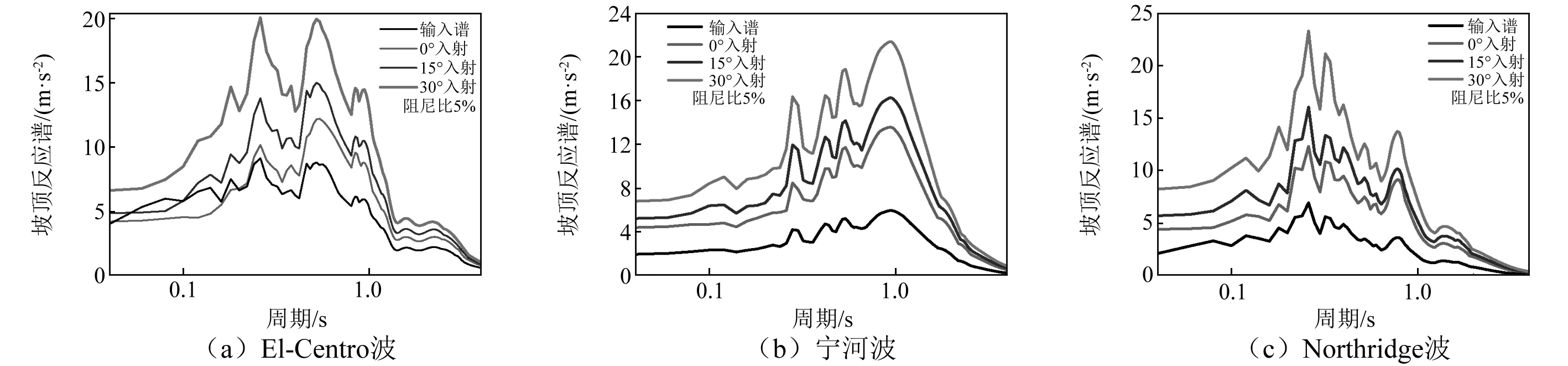
图14 45°坡不同地震波入射角度坡顶加速度反应谱Fig.14 Acceleration response spectra of slope crest in different incident angles under slope angle 45°

从图13可以看出，河谷斜坡坡顶处的反应谱与输入谱相比有明显的放大，且随斜坡坡度的增大，坡顶处的反应谱也增大，反应谱峰值有向右偏移的趋势，即坡顶处反应谱的特征周期有所增大。从图14可以看出，入射角度对坡顶反应谱的形状影响不大，入射角度越大，坡顶处加速度反应谱越大。入射角度对坡顶加速度反应谱的影响主要体现在短周期(0～1.5 s)分量上，1.5 s以后，入射角度对坡顶处反应谱形状的影响很小。

4 结 论

本文针对河谷地形，采用数值模拟的方法，探讨了河谷斜坡坡度和SV波入射角度对河谷场地地震动放大系数分布特征的影响，得出以下结论：

(1)河谷斜坡坡度对河谷场地地震动放大系数有较大影响。斜坡坡度越大，斜坡坡面以及坡顶平台一定范围的地震动放大系数越大，对坡顶平台的影响宽度也越大。

(2)地震波倾斜入射时，河谷两岸地震动放大系数与垂直入射时相比有较明显的差异。倾斜入射时河谷两岸地震动放大系数呈不对称形式分布，且入射角度越大，这种不对称现象越明显。

(3)当地震波从左侧入射时，入射角度越大，河谷左岸x向的地震动放大系数越大，河谷右岸z的地震动放大系数越大，但总体上x分量要大于z分量。在河谷场地的抗震分析中要考虑地震波入射角度的影响。

(4)以不同角度入射时，坡顶处地震动放大系数和坡顶平台的影响宽度随坡度的增大均呈线性增长趋势，且入射角度越大，线性增长速率越大。

(5)入射角度和斜坡坡度越大，坡顶处的反应谱越大。随着斜坡坡度的增大，反应谱峰值有向右偏移的趋势。入射角度对坡顶处反应谱形状的影响很小，其对坡顶加速度反应谱的影响主要体现在短周期(0～1.5 s)分量上。