波纹辊轧机辊系垂直非线性参激振动特性分析

和东平， 王 涛， 解加全， 任忠凯， 刘元铭

(太原理工大学 机械与运载工程学院，太原 030024)

轧机振动研究已有半个多世纪的历史，随着轧机朝着大型化、高速化、连续化、智能化的快速发展以及大量新技术的采用使轧机振动出现了许多新问题，常常表现为“幽灵”式多态耦合振动，主要包含轧辊的垂直振动、水平振动、轴向窜动、带钢的横向和纵向振动、主传动系统的扭转振动和轴向振动等，直接影响轧制过程稳定性和轧件质量，成为国内外众多学者和专家的研究热点[1-5]。

传统的复合板轧制生产工艺是轧机的上下工作辊都分别采用平辊与两种金属接触进行轧制生产，从而实现两种金属的横向与纵向延伸，但是在实际的生产中，由于上下两种金属的延伸率不一样，很容易造成金属大曲率翘曲，不能连续化生产(如图1所示)。复合板波纹辊轧制技术是一项变革性技术(如图2所示)，可以促进异种材料更好的实现冶金结合，提高结合强度，实现连续化生产。通过波纹辊轧制铜铝复合板的实验表明：铜铝复合板界面处的晶粒得到明显细化；铝侧晶粒细化程度明显高于铜侧；相同等效压下率下，波纹轧后拉伸过程中界面结合良好，界面处存在韧窝[6]。但是，波纹辊的辊形曲线为余弦函数曲线，在复合板的轧制过程中，轧制界面的非线性阻尼以及上下波纹辊之间的非线性刚度都可能导致参激振动的发生，造成辊缝的波动，从而影响复合板的生产质量和降低零部件的在线服役时间。

图1 平辊轧制翘曲现象Fig.1 Warping phenomenon of flat roll

图2 波纹辊轧制示意图Fig.2 Rolling diagram of corrugated roll

近些年来，国内外的科研人员针对轧机辊系振动的问题都做了许多有益的探索。Younes 等[7]将轧件等效为具有线性刚度的弹性零件，基于线性振动理论建立了轧机机座的线性垂振模型。Panjkovi等[8]认为负载钢材的规格和轧辊表面长期工作形成的表面氧化都是引起辊缝摩擦因数变化的原因，进而提出轧机辊缝的摩擦环境的变化是造成轧机系统颤振的一个原因。Kapil等[9]考虑移动板带振动导致的轧辊与轧件间的非线性参激特性，建立了一个单自由度的轧机非线性参激振动模型，并得到轧机振动的不稳定区域及幅频振动特性。侯东晓等[10]考虑冷轧机轧辊在垂直方向上振动位移动态变化影响，建立了一种动态轧制力模型。孙韵韵等[11]采用多尺度法求解了考虑界面粗糙形貌影响的轧机系统主共振幅频特性方程，分析了轧制界面粗糙形貌、激励载荷、非线性刚度率和阻尼对轧机辊系系统动力学响应特性的影响，为抑制轧机振动提供了有效的理论参考。彭荣荣等[12]建立了动态轧制力下的四辊冷连轧机非线性振动动力学模型，运用多尺度法求解得到了系统的超谐波共振和亚谐波共振。闫晓强等[13]通过对热连轧机的研究，发现轧机存在扭垂耦合振动、机电耦合振动和液机耦合振动现象，确定轧机振动的性质为机电液多态耦合振动。郜志英等[14]基于Slab分析法建立了轧制过程模型，并且将动态轧制力作为反馈激励源，作用于相应的轧机结构模型，从而构建了轧制过程与系统结构相耦合的颤振动力学模型。到目前为止，国内外对轧机振动的研究已取得了一定的成绩，但是影响轧机振动的因素较多，涉及到振动理论、轧制理论、故障诊断理论等几大领域的交叉融合。波纹辊轧机是一个多变量、强耦合、非线性、多约束、时变性的系统，波纹辊轧机的振动问题影响着产品的质量和零部件的在线使用寿命，但是，目前还没有学者针对波纹辊轧机辊系的振动特性展开相关研究。

基于上述原因，本文考虑了波纹辊轧机波纹界面间的非线性阻尼和非线性刚度，建立了波纹辊轧机两自由度垂直非线性参激振动模型。利用奇异值理论讨论了波纹辊轧机辊系自治下的稳定性，运用多尺度法求解了波纹辊轧机辊系在波纹界面激励下的主共振和次共振的解析近似解和幅频特性方程。分析了非线性刚度、非线性阻尼、系统阻尼、轧制力的幅值等参数对振动的影响。通过数值仿真验证了分析结果的正确性，为抑制波纹辊轧机的辊系振动提供了一定的理论指导。

1 波纹辊轧机辊系垂向振动测试分析

以实验室波纹辊轧机作为实验对象，采用现代振动测试技术，建立了波纹辊轧机辊系振动检测系统。对复合板的轧制过程进行综合测试与对比，深入了解波纹辊轧机辊系的振动特性与平辊轧制复合板辊系振动特性的区别。板材前进的方向定义为X方向，平行于轧辊的方向定义为Y方向，垂直于XY方面的方向定义为Z方向。小型波纹辊轧机主要参数如下：

电机功率： 3 kW

波纹辊直径(波腰)： 95 mm

平轧辊直径： 95 mm

三向加速度传感器型号： HD-YD-230

16通道数据采集仪： INV3060A

分析软件： DASP2010

试验工况：转速为0.18 m/s，压下量50%

在平辊轧制铜铝复合板和波纹辊轧制铜铝复合板过程中，针对操作侧的上工作辊轴承座三个方向的加速度信号进行频谱对比分析。检测结果如图3～图8所示。

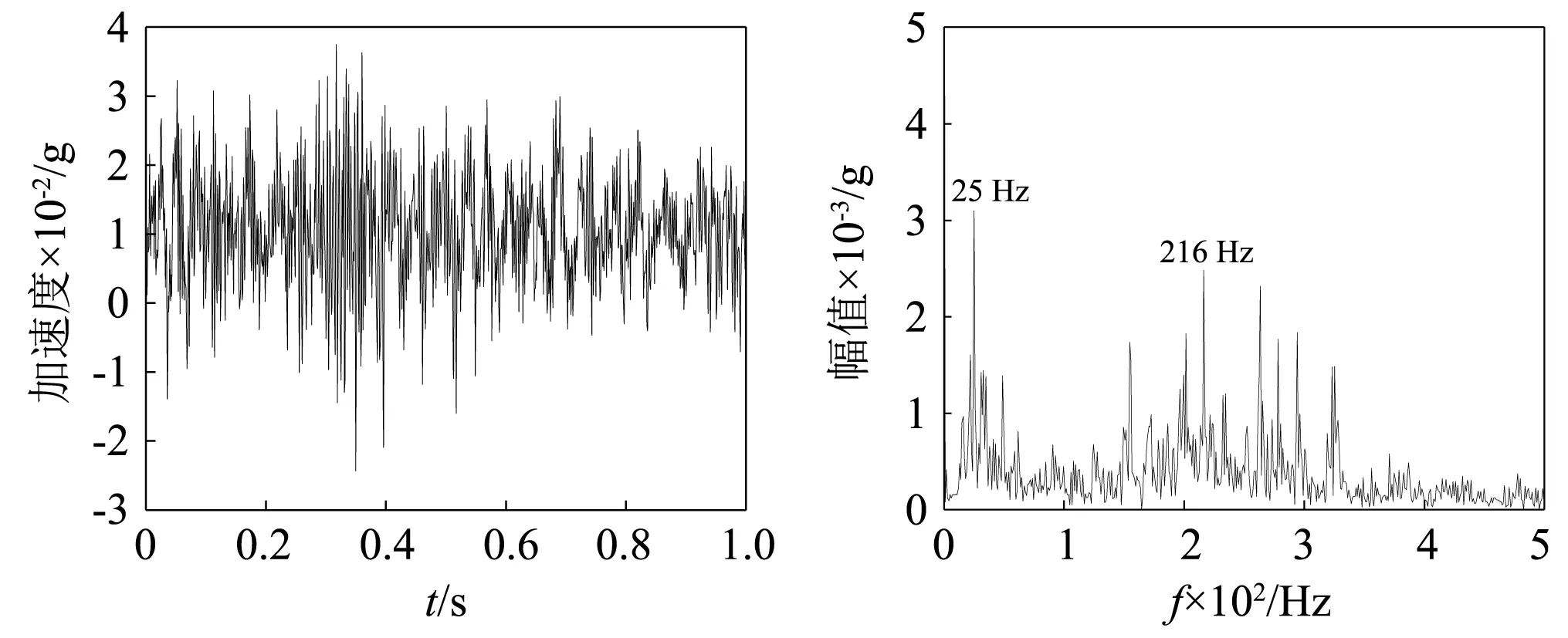
图3 平辊轧制X方向时域频谱图Fig.3 X-direction time-domain spectrogram of flat rolling

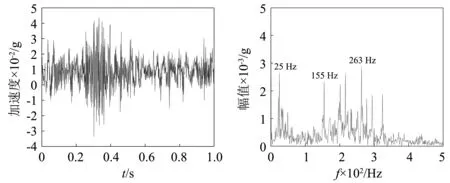
图4 平辊轧制Y方向时域频谱图Fig.4 Y-direction time-domain spectrogram of flat rolling

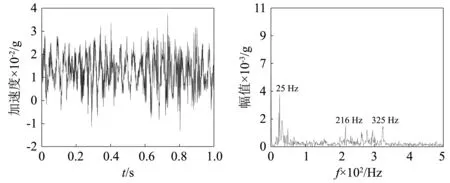
图5 平辊轧制Z方向时域频谱图Fig.5 Z-direction time-domain spectrogram of flat rolling

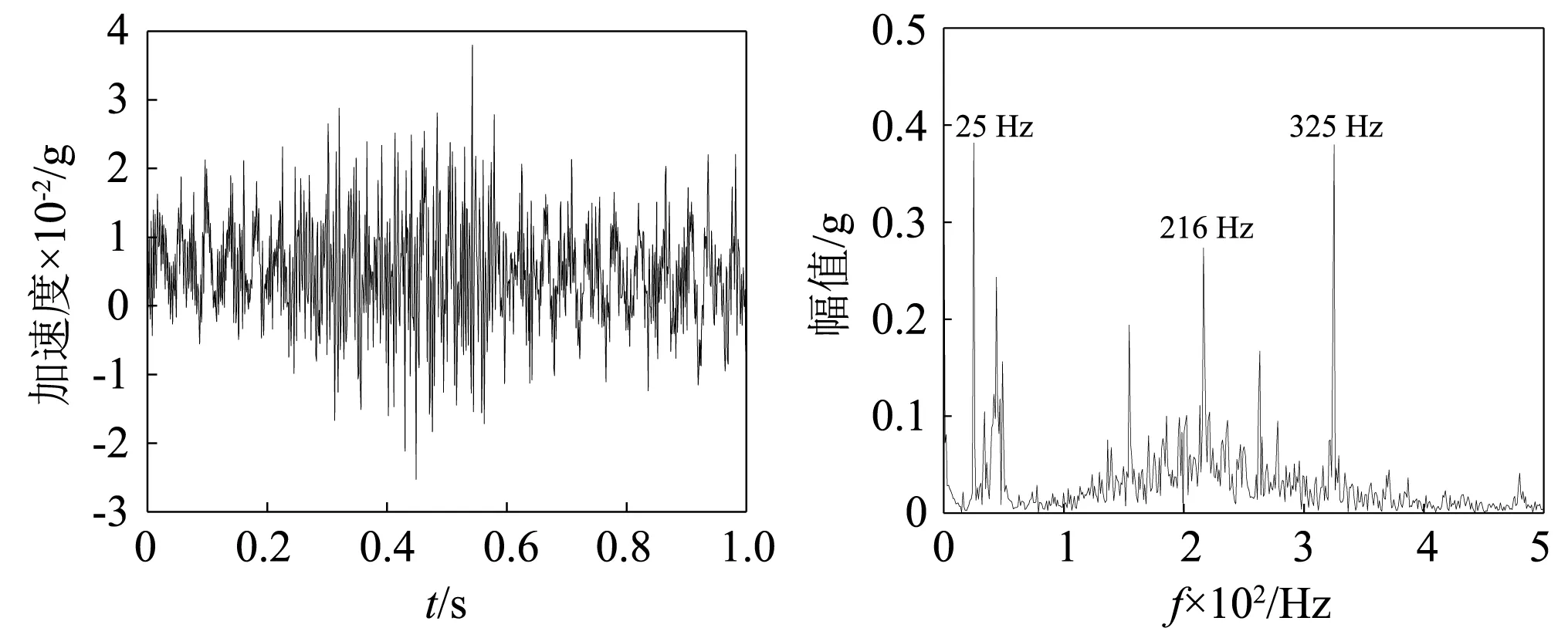
图6 波纹辊轧制X方向时域频谱图Fig.6 X-direction time-domain spectrogram of corrugated rolling

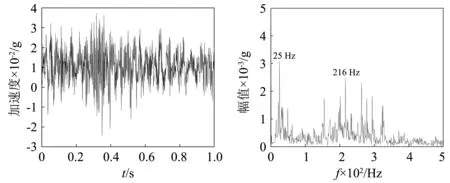
图7 波纹辊轧制Y方向时域频谱图Fig.7 Y-direction time-domain spectrogram of corrugated rolling

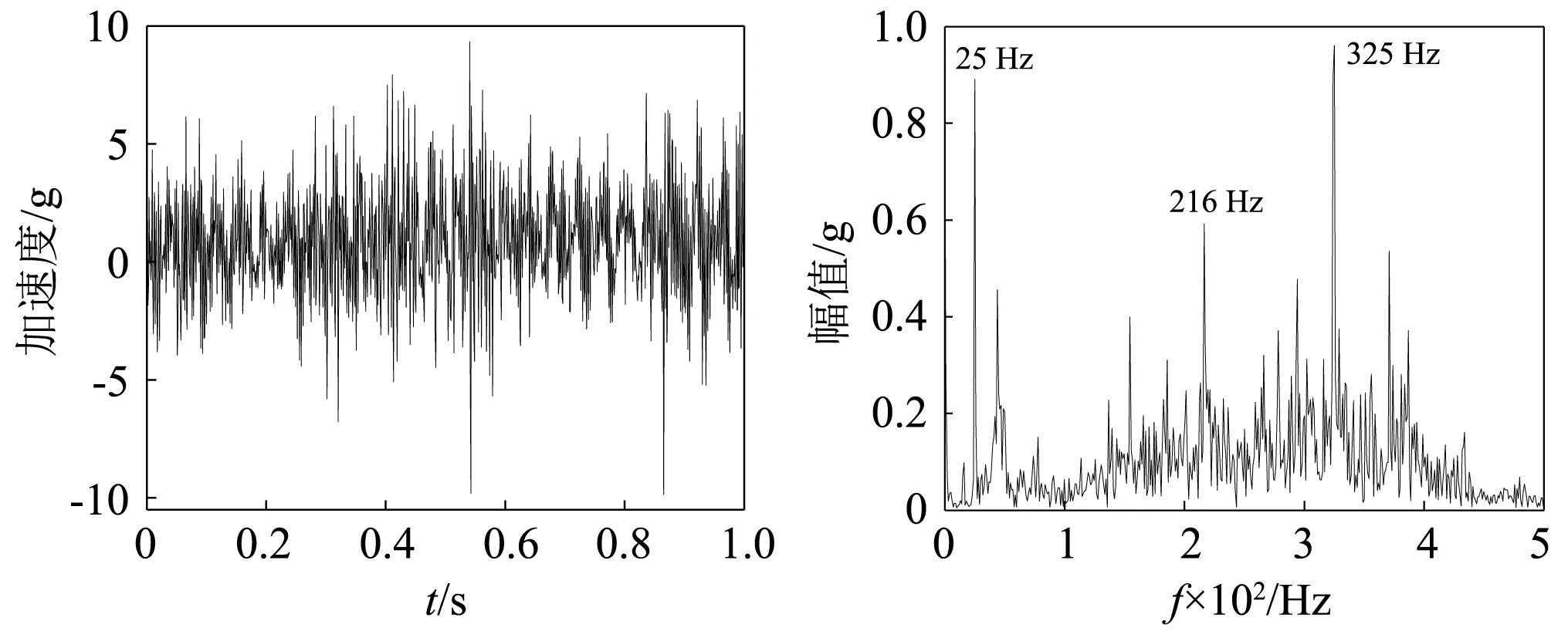
图8 波纹辊轧制Z方向时域频谱图Fig.8 Z-direction time-domain spectrogram of corrugated rolling

通过分析平辊轧制铜铝复合板和波纹辊轧制铜铝复合板操作侧上工作辊轴承座三向加速度信号的时域频谱图可以得到：当转速为0.18 m/s、压下量50%时，平辊轧制过程中操作侧的上工作辊轴承座的优势频率为25 Hz、216 Hz、155 Hz、263 Hz、325 Hz，波纹辊轧制过程中操作侧的上工作辊轴承座的优势频率为25 Hz、216 Hz、325 Hz。相同工况、相同检测位置、相同方向，波纹辊轧制过程中振动明显比平辊轧制复合板过程剧烈。推断振源发生在轧制变形区，由于辊形曲线造成的非线性阻尼和非线性刚度等多参数耦合的非线性参激共振所导致。因此需要从理论上对波纹辊轧机辊系的振动特性进行更加深入的研究，以便为抑制波纹辊轧机的辊系振动提供理论指导。

2 波纹辊轧机辊系非线性参激振动模型

本文研究对象为电动压下波纹辊轧机，没有压下缸和弯辊缸，所以忽略压下缸和弯辊缸的非线性弹性力和非线性摩擦力对参激振动的影响，只考虑波纹辊轧制界面的非线性阻尼以及波纹辊之间的非线性刚度，波纹辊轧机可以简化为两自由度垂直非线性参数振动模型，如图9所示。

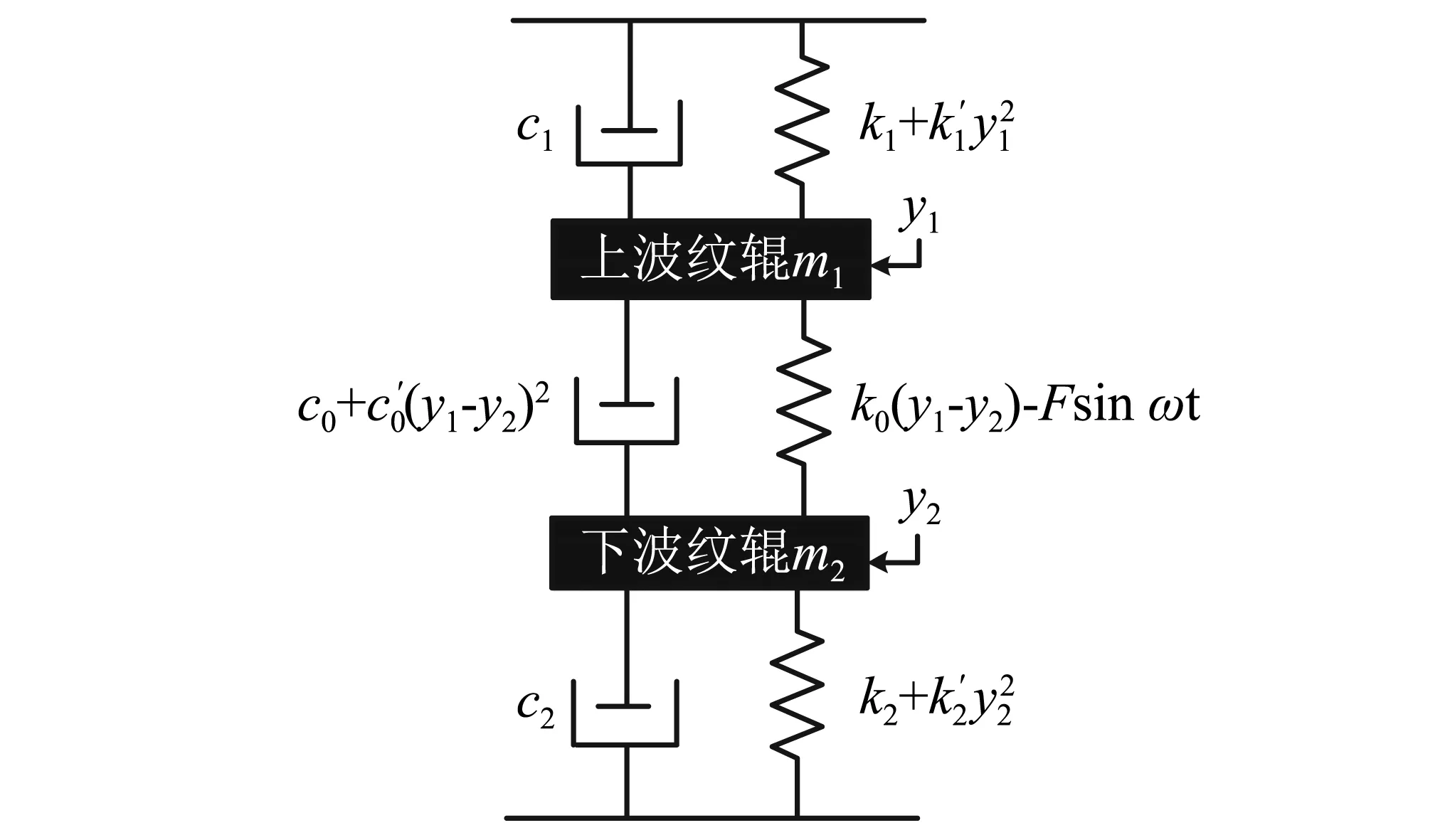
图9 波纹辊系参激振动数学模型Fig.9 Parametrically excited vibration mathematical model of corrugated roll

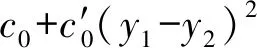
(1)

在波纹辊轧制复合板的过程中，上下波纹辊系具有基本对称性。因此令m1=m2，y1=-y2，则式(1)可以简化为

(2)

将式(2)无量纲化，

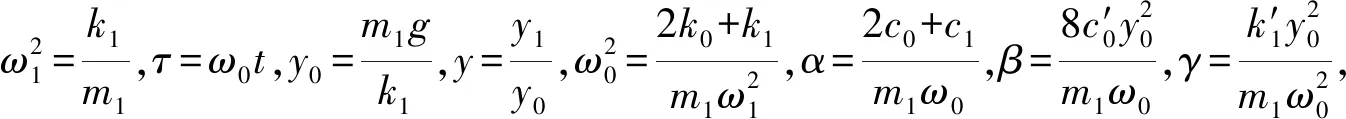
则两自由度非线性振动微分方程可以简化为

(3)

假设ε为小参数，将式(3)的非线性项冠以为小参数ε，则有

(4)

3 波纹辊轧机辊系稳定性分析

波纹辊辊系的稳定性对复合板的生产质量有着重要的影响。基于奇异值理论，对波纹辊辊系在自治状态下的稳定性进行分析[15]。

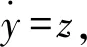
(5)

得到波纹辊轧机自治系统的雅克比矩阵为

(6)

由式(5)可知，

当γ>0时，自治系统的奇点为(0,0)。

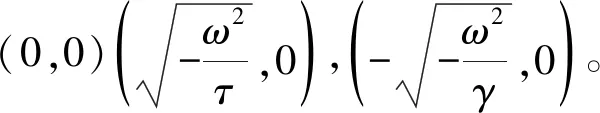
当γ>0时，将奇点代入式(6)得到

(7)

式(7)的特征方程为

(8)

解得

(9)

当ω0>0，2ω0<α<2.3ω0时，奇点为稳定节点，系统渐进稳定；

当ω0>0，α=2ω0时，奇点为稳定边界节点，系统渐进稳定；

当ω0>0，α<2ω0时，奇点为稳定节点，系统渐进稳定；

当ω0>0，α>2.3ω0和α<-2ω0时，奇点为不稳定节点，系统不稳定；

当ω0>0，α=-2ω0时，奇点为不稳定节点，系统不稳定；

当ω0>0，α>-2ω0时，奇点为不稳定节点，系统不稳定；

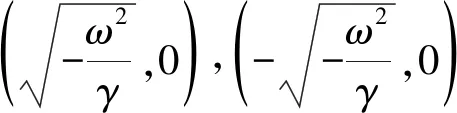
(10)

式(10)的特征方程为

(11)

解得

(12)

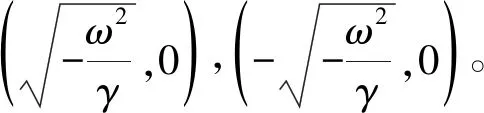
4 波纹辊轧机参激振动求解

波纹辊轧机是一个非线性振动系统，在轧制的过程中可能导致多种共振现象，如：内共振、主参数共振、倍共振。下面主要讨论波纹辊的轧制力的激振频率ω接近固有频率ω0时的主参数共振、超谐波共振、亚谐波共振进行分析[16-17]。

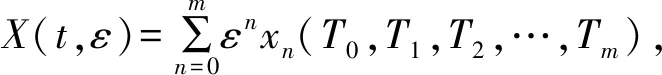
Y(t,ε)=Y0(T0,T1)+εY1(T0,T1)+…

(13)

将不同尺度的时间变量视为独立变量，则X(t,ε)成为m个独立时间变量的函数，对时间的微分可利用复合函数微分公式按ε的幂次展开，

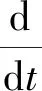
(14)

(15)

其中Dn(n=0,1,2,…,m)为偏微分算子，定义

4.1 主共振响应求解

假设ζ为频率调制参数。讨论波纹辊轧制力的激振频率ω接近波纹辊轧机固有频率ω0时[18]，令

(16)

将式(13)～式(15)代入式(4)，展开后令两边的同次幂系数相等，得到各阶近似方程：

(17)

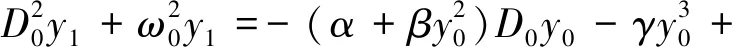
(18)

设零次近似方程(17)的解为

y=B(T1)ejω0T0+Δ

(19)

式中：Δ代表前一项的共轭复数。

将式(19)代入式(18)，得到

(20)

为了避免出现久期项，必须使函数B满足：

(21)

将B表示成复数形式，令

(22)

将式(22)代入式(21)，分离实部与虚部，得到

(23)

(24)

令φ=ζt-φ，化简式(23)和式(24)可得主共振一阶近似解：

Y=kcos(ω0t+φ)+O(ε)

(25)

(26)

改变波纹辊轧机的非线性刚度系数γ、非线性阻尼系数β、系统阻尼系数α、轧制力的幅值F，可以得到不同的主共振幅频特性曲线(扰动频率ζ与k振幅之间的关系)。

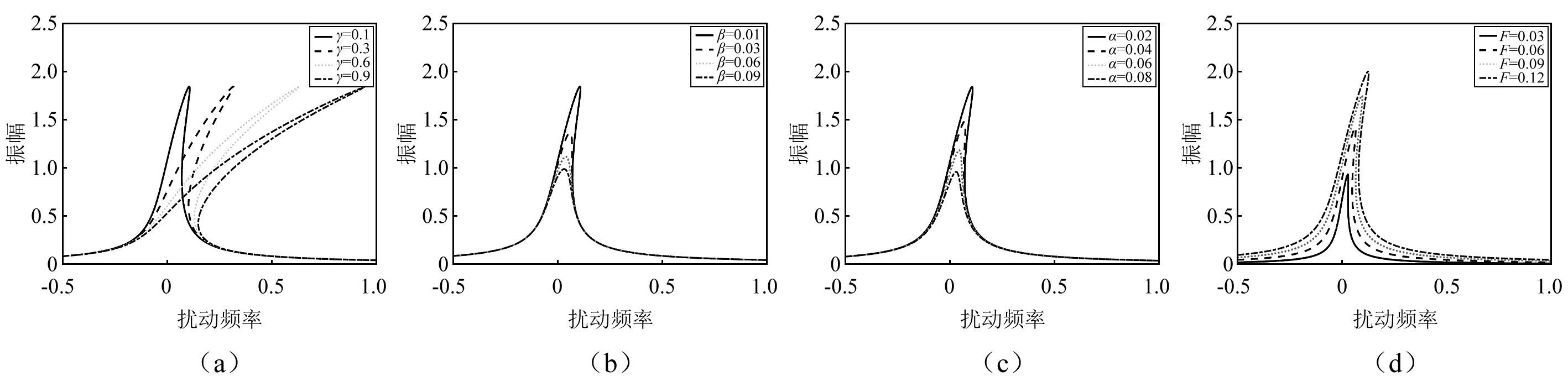
图10 不同参数对主共振幅频特性曲线的影响Fig.10 The amplitude-frequency characteristic curve of principal resonance with different parameters

如图10(a)所示，随着非线性刚度系数γ的增大，曲线右移而且弯曲程度增大。当扰动频率从负值到正值变化的时候，幅值出现跳跃，引起系统的振荡。如图10(b)所示，随着非线性阻尼系数β的增大，振幅减小且共振域减小。如图10(c)所示，随着系统阻尼系数α的增大，振幅减小且共振域减小。非线性阻尼系数β和系统阻尼系数α的变化不影响频响曲线的弯曲程度。如图10(d)所示，随着轧制力的幅值F的增大，系统的振幅和共振区域明显增大。因此，在波纹辊设计的过程中，可以通过减小波峰与波谷之间的距离、减少波纹的数量来对辊形曲线进行优化设计从而避免和减小轧制力幅值对主共振的影响。

4.2 次共振响应求解

当波纹辊轧制力的激振频率ω接近波纹辊轧机固有频率ω0的整数倍或者分数倍时，出现的共振现象，分别称为超谐波共振或者亚谐波共振，统称为次共振。

将式(4)中的εFcosωt以Fcosωt代替，只讨论一次近似解，将式(15)代入式(4)得到：

(27)

(28)

设零次近似方程(27)的解为

y=B(T1)ejω0T0+CejωT0+Δ

(29)

式中：Δ代表前一项的共轭复数。

(30)

将式(29)代入式(28)得到：

(31)

式中：Δ代表前一项的共轭复数。

4.2.1 超谐波共振响应求解

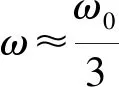
3ω=ω0+εζ

(32)

将式(32)代入式(31)，令ejω0T0的系数为零以消除久期项，得：

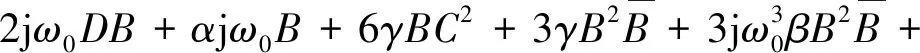
(33)

将B表示成复数形式，令

(34)

将式(34)代入式(33)，分离实部与虚部，得到

(35)

(36)

令φ=ζt-φ，化简式(35)和式(36)可得超谐波共振一阶近似解：

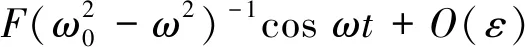
(37)

(38)

改变波纹辊轧机的非线性刚度系数γ、非线性阻尼系数β、系统阻尼系数α、轧制力的幅值F，可以得到不同的超谐波共振幅频特性曲线(扰动频率ζ与振幅k之间的关系)。

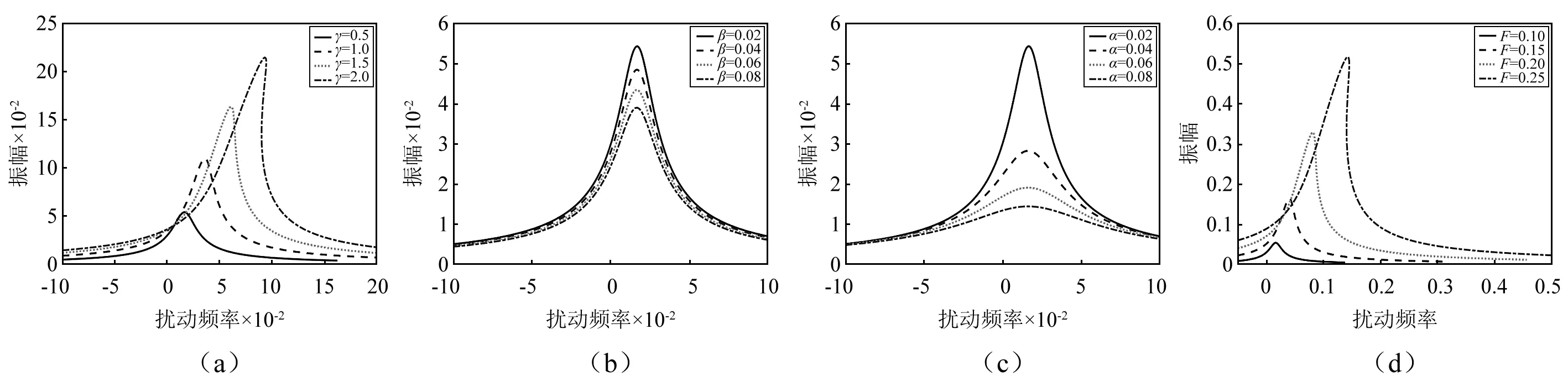
图11 不同参数对超谐波共振幅频特性曲线的影响Fig.11 The amplitude-frequency characteristic curve of super-harmonic vibration with different parameters

如图11(a)所示，随着非线性刚度系数γ的增大，骨干曲线右移而且弯曲程度增大,振幅和共振区域增大。当扰动频率从负值到正值变化的时候，幅值出现跳跃，引起系统的振荡。如图11(b)所示，随着非线性阻尼系数β的增大，振幅减小且共振域减小。如图11(c)所示，随着系统阻尼系数α的增大，振幅减小且共振域减小。非线性阻尼系数β和系统阻尼系数α的变化对振幅和共振区域的影响小。如图11(d)所示，随着轧制力的幅值F的增大，骨干曲线右移，系统的振幅和共振区域明显增大。因此，在波纹辊设计的过程中，可以通过减小波峰与波谷之间的距离、减少波纹的数量来对辊形曲线进行优化设计从而避免和减小轧制力幅值对超谐波的影响。

4.2.2 亚谐波共振响应求解

当ω≈3ω0时，系统发生亚谐波共振响应，设ω与3ω0的差别为ε的同阶小量，令

ω=3ω0+εζ

(39)

将式(39)代入式(31)，令ejω0T0的系数为零以消除久期项，得：

(40)

将B表示成复数形式，令

(41)

将式(41)代入式(40)，分离实部与虚部，得到

(42)

(43)

令φ=ζt-3φ，得到

(44)

(45)

化简式(44)和式(45)可得超谐波共振一阶近似解：

(46)

(47)

改变波纹辊轧机的非线性刚度系数γ、非线性阻尼系数β、系统阻尼系数α、轧制力的幅值F，可以得到不同的亚谐波共振幅频特性曲线(扰动频率ζ与振幅k之间的关系)。

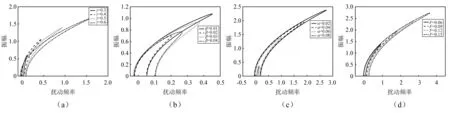
图12 不同参数对亚谐波共振幅频特性曲线的影响Fig.12 The amplitude-frequency characteristic curve of sub-harmonic vibration with different parameters

如图12(a)所示，随着非线性刚度系数γ的增大，曲线右移而且弯曲程度增大。当扰动频率从负值到正值变化的时候，幅值出现跳跃，引起系统的振荡。如图12(b)所示随着非线性阻尼系数β的增大，振幅减小且共振域减小。如图12(c)所示随着系统阻尼系数α的增大，振幅减小且共振域减小。非线性阻尼系数β和系统阻尼系数α的变化对振幅和共振区域的影响小。如图12(d)所示随着轧制力的幅值F的增大，系统的振幅和共振区域明显增大。因此，在波纹辊设计的过程中，可以通过减小波峰与波谷之间的距离、减少波纹的数量来对辊形曲线进行优化设计从而避免和减小轧制力幅值对亚谐波的影响。

5 结 论

(1)本文考虑了波纹辊轧机波纹界面间的非线性阻尼和非线性刚度，建立了波纹辊轧机两自由度垂直非线性参激振动模型。

(2)利用奇异值理论讨了波纹辊轧机辊系自治下的稳定性，运用多尺度法求解了波纹辊轧机辊系在波纹界面激励下的主共振和次共振的解析近似解和幅频特性方程。

(3)通过数值仿真分析了非线性刚度系数、非线性阻尼系数、系统阻尼系数、轧制力的幅值等参数对波纹辊轧机辊系垂直非线性参激振动的影响，验证了分析结果的正确性，为抑制波纹辊轧机的辊系振动和升级改造提供了一定的理论指导。

(4)在波纹辊的设计过程中，可以通过减小波峰与波谷之间的距离、减少波纹的数量来对辊形曲线进行优化设计从而减小参激振动对轧制过程的影响。