梳齿密封静态稳定性理论与实验研究
马 凯, 张万福, 张 尧, 顾乾磊, 陈璐琪, 李 春, 杨建刚
(1. 上海理工大学 能源与动力工程学院 流体机械及工程研究所,上海 200093;2. 东南大学 火电机组振动国家工程研究中心,南京 210096)
梳齿密封作为工业中一种常见的密封形式,被广泛的应用于压缩机、燃气轮机、汽轮机等旋转机械。工质在梳齿密封中的流动通常是复杂的三维湍流,当转子因径向弯曲、不同心或旋转涡动时,梳齿密封腔内会产生一个作用于转子上的密封气流力,从而导致转子失稳。随着透平机械向高参数和大容量方向发展,密封气流激振成为威胁机组安全运行的主要因素之一。梳齿密封作用于转子的激振力可分为静态力和动态力。静态力是转子零转速或无涡动下受到的静态激振力;动态力主要是由于转子振动产生的动态激振力。静态力对转子的影响主要表现为改变转子系统刚度,引起转子临界转速的变化,进而导致转子不稳定振动区域的改变,特别是密封负刚度会导致系统出现静态不稳定,工程实际中具有负静态直接刚度的密封会引起轴系临界转速的降低、并会进一步促进转子向完全偏心发展,进而产生密封碰磨而失效[1-2]。
Lomakin在1958年第一次提出光滑环形密封由于轴向压降会导致正的直接径向刚度的产生,且与转速无关,是雷诺数、压降、密封半径、密封间隙的函数,该效应也随之被称为“Lomakin效应”。张盟等[3]发现对于不可压缩流体,较长的等截面环形密封容易产生负直接刚度。Fleming[4]最先计算了以空气为介质的光滑环形密封径向刚度,发现该密封会出现负刚度。Alexander等[5-6]在实验中发现光滑环形密封会出现使转子远离平衡位置的静态扰动力(de-centering force),进而会产生静态不稳定问题。Arghir等[7-8]指出负刚度是密封内发生阻塞流动所致,并对阻塞流动下流场特性进行了分析。然而,Childs等[9]通过实验发现在没有发生阻塞流动情况下,也会产生不稳定的静态扰动力和负刚度,Arghir等[10]针对该密封开展了理论分析,指出在静态大偏心情况下,传统的Lomakin效应被具有较小雷诺数的小间隙内黏性力效应减弱,从而导致负刚度的产生。李志刚等[11]对高偏心率下袋型阻尼密封的静态动力特性进行了研究,发现在偏心率小于0.5,且密封出口流动发生阻塞时,袋型阻尼密封会产生负的直接刚度,但并没有解释负直接刚度产生的原因。
然而,在对梳齿密封稳定性研究中也出现了许多负直接刚度的现象。Benckert等[12]做了大量的关于密封动力特性实验,指出密封交叉刚度是由周向流动引起,并发现较长密封的直接刚度为负值。Leong等[13]对汽轮机迷宫密封做了大量试验,结果与Benckert等的测量结果很吻合,多数密封直接刚度为负,少量短密封为正。Childs等[14]通过实验和理论分别对齿在转子和静子上的迷宫式密封进行了研究,在不同转速和密封间隙下,二者都产生了负直接刚度,与理论计算值相吻合。Picardo等[15]对梳齿密封进行了测试,密封静态刚度系数为负,实验中需在密封外侧的水平方向上设置了四个顶杆以消除定子的不稳定性。Mehta等[16]在实验中发现,由于定子是柔性支撑,在零转速下随着进气压力的增大,定子会朝着转子的方向移动,为了消除这种静态不稳定现象,Mehta在原实验装置基础上进行了改进,即在密封的垂直方向上增加了顶杆。何立东等[17-19]通过实验和数值方法对不同压比、不同转速下的密封动力特性系数进行了研究,结果发现实验测量和数值计算结果有一致性。孙婷梅[20]利用Fluent计算迷宫密封三维流场,研究了偏心率、入口预旋、涡动速度对密封动力特性的影响,密封直接刚度维持在负值范围。然而,梳齿密封静态不稳定形成机理尚不明确。
本文以梳齿密封为研究对象,通过实验和理论研究密封静态稳定性及形成机理。实验测试了不同偏心率不同进口压力下梳齿密封零转速时的静特性变化,并应用计算流体力学方法研究了实验密封内流体流动特性。
1 密封静态稳定性实验研究
1.1 实验装置
本文首先在透平机械流体激振实验台上开展静态稳定性实验研究,转子-密封系统实验装置与密封内部结构如图1和图2所示。为了放大气流力的影响,气缸采用弹性支撑方式,垂直和水平方向分别采用四组拉簧支撑。与刚性支撑相比,该装置有如下优点:①由于气流力较小,识别难度大,通过这种方法可以放大气流力作用下气缸的振动响应,提高气流力识别精度;②便于以气缸为对象对密封气流力与动力特性系数进行识别,避免以固定式气缸为对象或基于转子动态响应识别带来的误差;③便于调整密封间隙,以得到不同偏心的密封状态。

1.转子 2.#1轴承 3.透平油 4.气缸 5.弹性支撑系统 6.密封进气管路 7. #2轴承 8.电涡流位移传感器 9.百分表 10.压力传感器 11.平衡盘 12.光电传感器 图1 转子-密封系统实验装置Fig.1 Rotor-seal system experimental device

1.密封齿 2.弹性支撑片 3.气缸 4. 测压孔 5. 固定拉环 6.进气接口 7.进气孔 图2 气缸与密封结构实物图Fig.2 Cylinder and seal
密封采用中间进气方式,在气缸中部共布置4个周向对称的进气口,高压气体从4个进气口进气并经过密封腔室向两端排出,最高进气压力达0.8 MPa。密封二维截面模型与局部尺寸如图3所示,表1给出了密封具体几何尺寸。
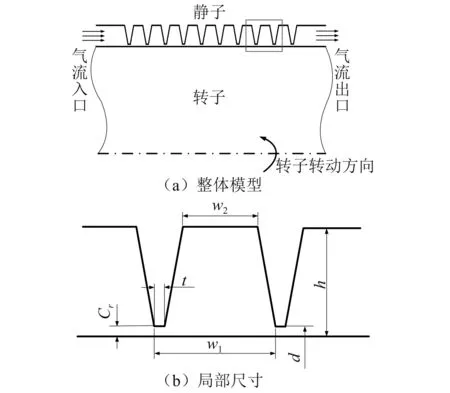
图3 密封模型几何尺寸Fig.3 Two-dimensional geometric model diagram of the seal

参数数值长度l/mm34.2直径d/mm60.2间隙Cr/mm0.1齿数10密封腔宽度w1/mm3.8密封腔顶部宽度w2/mm2.3齿厚度t/mm0.25密封腔高度h/mm3.4
1.2 静态刚度系数实验识别方法
为识别密封气流力与刚度系数,需要先对系统原始刚度进行实验测试。在无偏心的情况下,在气缸上施加不同载荷,测试气缸位移量并通过插值法可得对应的系统刚度系数,表2给出了载荷与系统刚度系数测试结果。

表2 系统刚度测量结果Tab.2 System stiffness measurement results
当转子在静平衡位置上受到位移或速度扰动时,作用在转子上的气流力与扰动之间是非线性的,当扰动是微小量时,可简化为线性关系,即
(1)
式中:Fx,Fy分别为密封气流力在x,y方向上的分量;Fx0,Fy0分别为静平衡位置时,密封气流力在x,y方向上的分量。
(2)
定义密封阻尼系数为单位速度所引起的气流力增量,即
(3)
由式(1)可得到密封气流力的增量,即动态力为
(4)
其中,
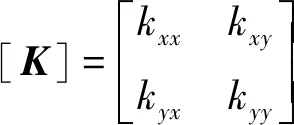
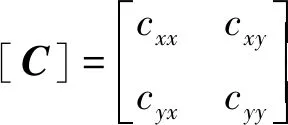
在动态分析中,把坐标的原点设在转子中心的静平衡位置, 令x,y为转子的动态位移,fx,fy为密封气流力,于是上式通常写为
(5)
在转子静态偏心时的密封激振力可进一步简化为
(6)
密封在Y方向偏心距为e时, 可得静态直接刚度系数(kxx,kyy)和静态交叉刚度系数(kxy,kyx)
(7)
本实验转子受力情况如图4所示,向下偏心,偏心距为e。
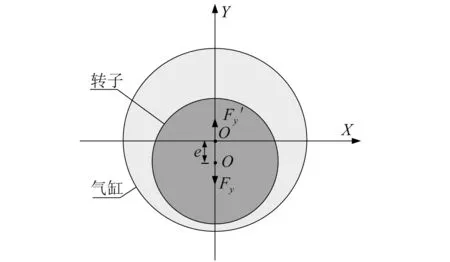
图4 实验气缸-密封系统模型Fig.4 Experimental cylinder-seal system model
通气后,转子受到的气流力为Fy,气缸受到的气流力为F′y,为作用力与反作用力
Fy=-F′y
(8)
由于转子固定而气缸由弹簧系统支撑, 气缸相对于转子会产生相对位移Δy, 因此气流力为
Fy=-F′y=KΔy
(9)
式中:K为在位移Δy下对应的系统刚度。
1.3 实验结果与分析
实验共测试了5种偏心工况,偏心率分别为80%, 60%, 40%, 20%及0%(同心状态)。在各偏心工况下,分别测试6组压比下气缸偏移情况。
如图5所示,在5种偏心情况下转子所受气流力随进口压力增加而增大。随着偏心率增大,在偏心0%~60%时,气流力也不断增大,且密封气流力方向与转子偏心方向相同。然而,偏心率80%下的气流力突然变小,这主要是在80%的偏心条件下,通气后转子与气缸发生接触,限制了气缸的运动,即静态不稳定现象。
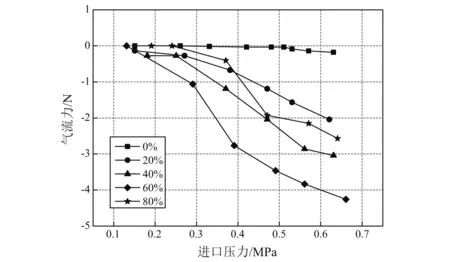
图5 不同偏心状态下转子所受气流力随进口压力的变化Fig.5 The force of air flow with the pressure of the rotor under different eccentric conditions
图6给出了不同进气压力下密封气流力和刚度系数随偏心率的变化情况。可以看出:①密封静态刚度系数都为负值;②随着进口压力的增大,密封气流力和静态刚度系数也随之增大;③同一进口压力下,密封气流力和静态刚度系数随着偏心率增大而增加,静态刚度系数大约为在-120 ~-15 kN/m。
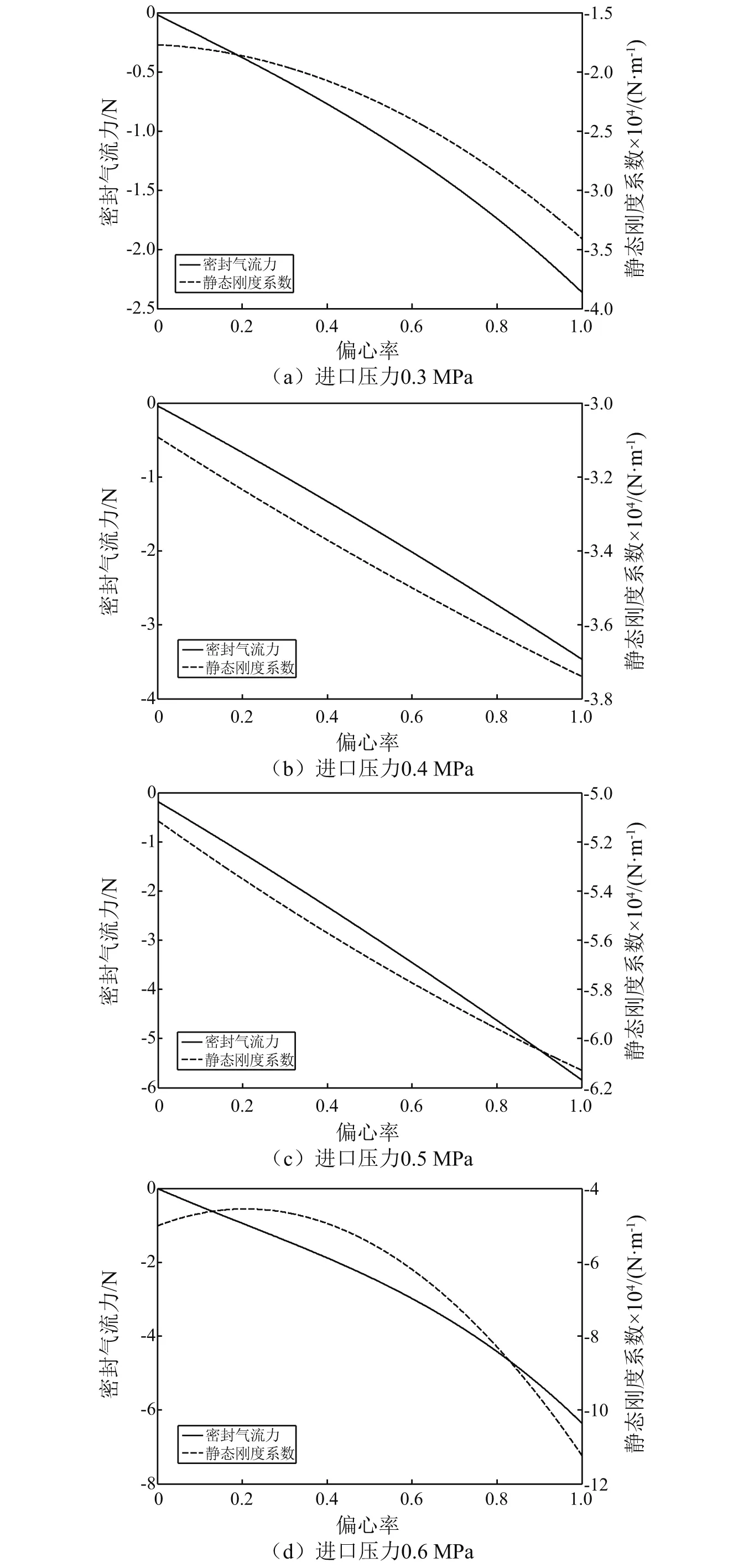
图6 不同进气压力下气流力和刚度系数随偏心率变化情况Fig.6 Variations of airflow force and stiffness coefficient with eccentricity under different inlet pressures
2 数值模型
以上文实验密封结构为对象,使用前处理器GAMBIT建立梳齿密封全三维计算模型。为了提高计算精度,采用了结构化网格,在流动变化剧烈的齿顶处进行适当加密,并对网格进行无关性验证:以密封偏心40%、进口压力为0.371 MPa为验证算例,设置不同体网格尺寸,进行网格无关性验证。表3给出了网格总数对计算结果的影响,最终网格数量确定为73万。图7分别给出了密封的计算域和计算网格图。边界条件为压力入口边界、压力出口边界,计算中固定出口压力,通过改变进口总压来模拟计算不同实验工况下密封气流力。
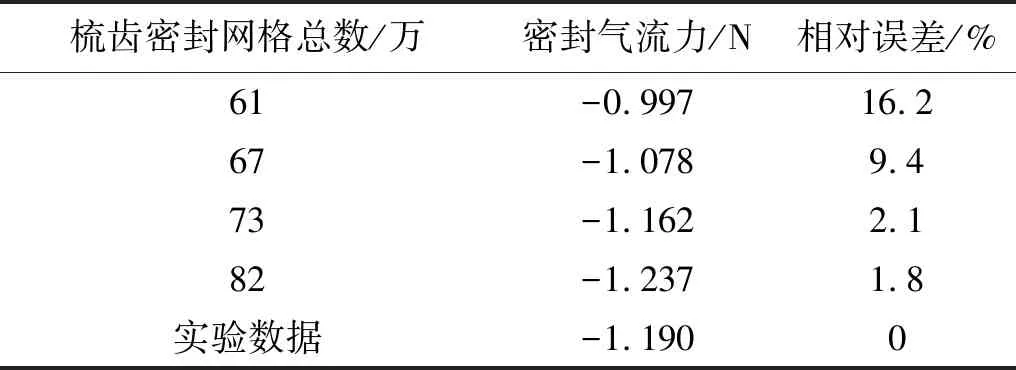
表3 网格无关性验证Tab.3 Grid independent verification
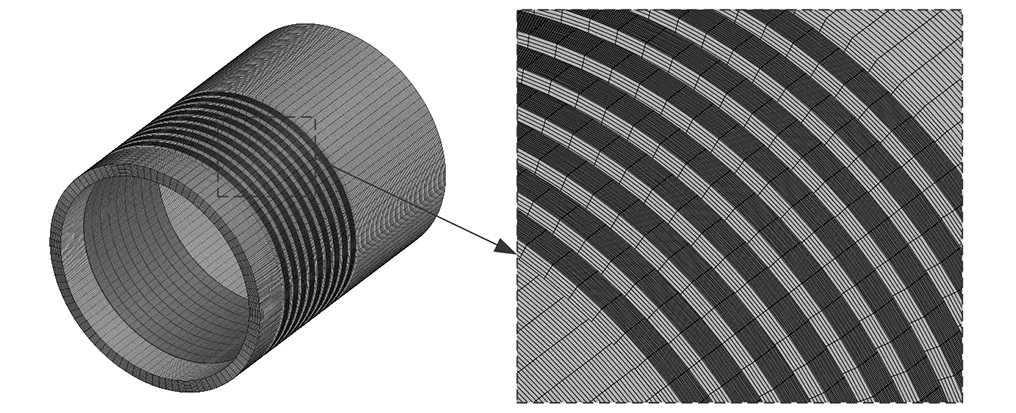
图7 计算网格示意图Fig.7 Schematic diagram of computation grid
本文应用ANSYS-CFX共计算了7种偏心率(0,0.2,0.4,0.6,0.8, 0.9,0.95)、6种进口压力工况,表4则给出了具体工况。
3 结果与讨论
3.1 气流力
图8给出了不同偏心状态下气流力随进口压力变化情况。可以看出,随着偏心率的增大,气流力不断增加;在每种偏心率下,气流力随着进口压力的增大呈线性增加。
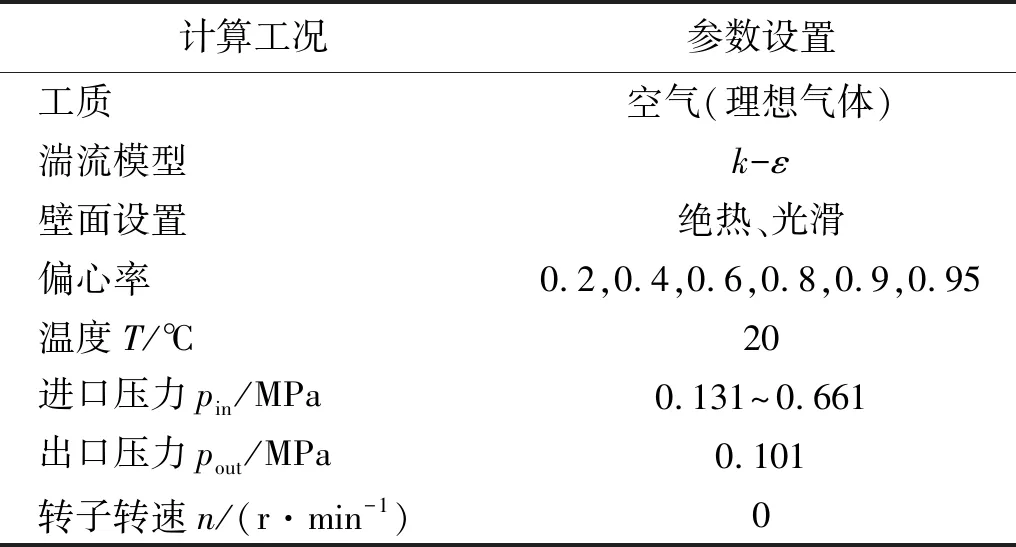
表4 工况参数Tab.4 Calculation conditions
图9对比了数值计算与实验测试所得气流力,可以看出在0%,20%,40%,60%偏心情况下,气流力随偏心率和进口压力的增大而不断增加,并且数值模拟数据与实验数据的十分接近,误差较小。然而在偏心80%情况下误差普遍偏高,这是由于实验中密封静态不稳定所致。
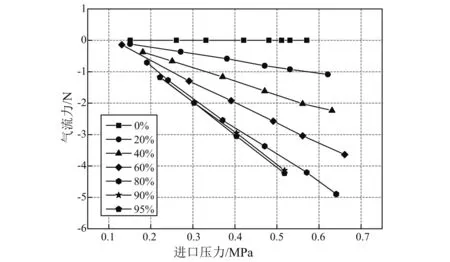
图8 不同偏心状态下气流力随进口压力的变化Fig.8 Variation of airflow force with inlet pressure under different eccentric states
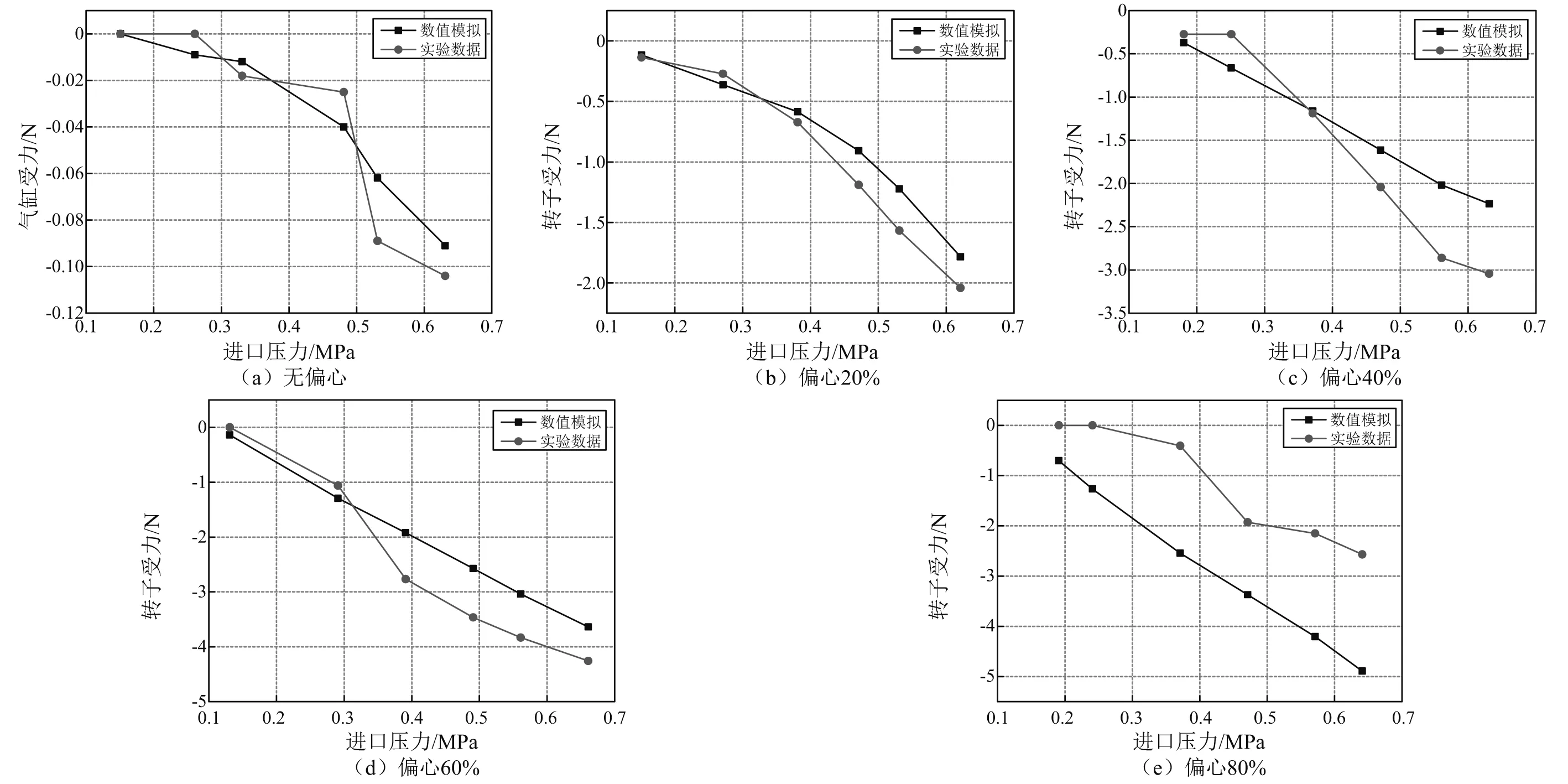
图9 计算数据与实验数据对比Fig.9 Comparing CFX data with experimental data
3.2 密封静态刚度系数
图10给出了静态刚度系数的实验测试与数值计算结果。可以看出,数值计算的静态刚度系数与实验结果非常吻合,特别是在进口压力为0.4 MPa和0.5 MPa时,误差最小。主要是因为实验压力在过低情况下,气缸静态偏移较小,测试误差较大,而过高时气缸与转子易产生局部碰摩,从而导致测试结果也会出现误差。在不同进口压力下,刚度都随着偏心率的增大而增大,静态刚度变化范围大约为-120~-15 kN/m。
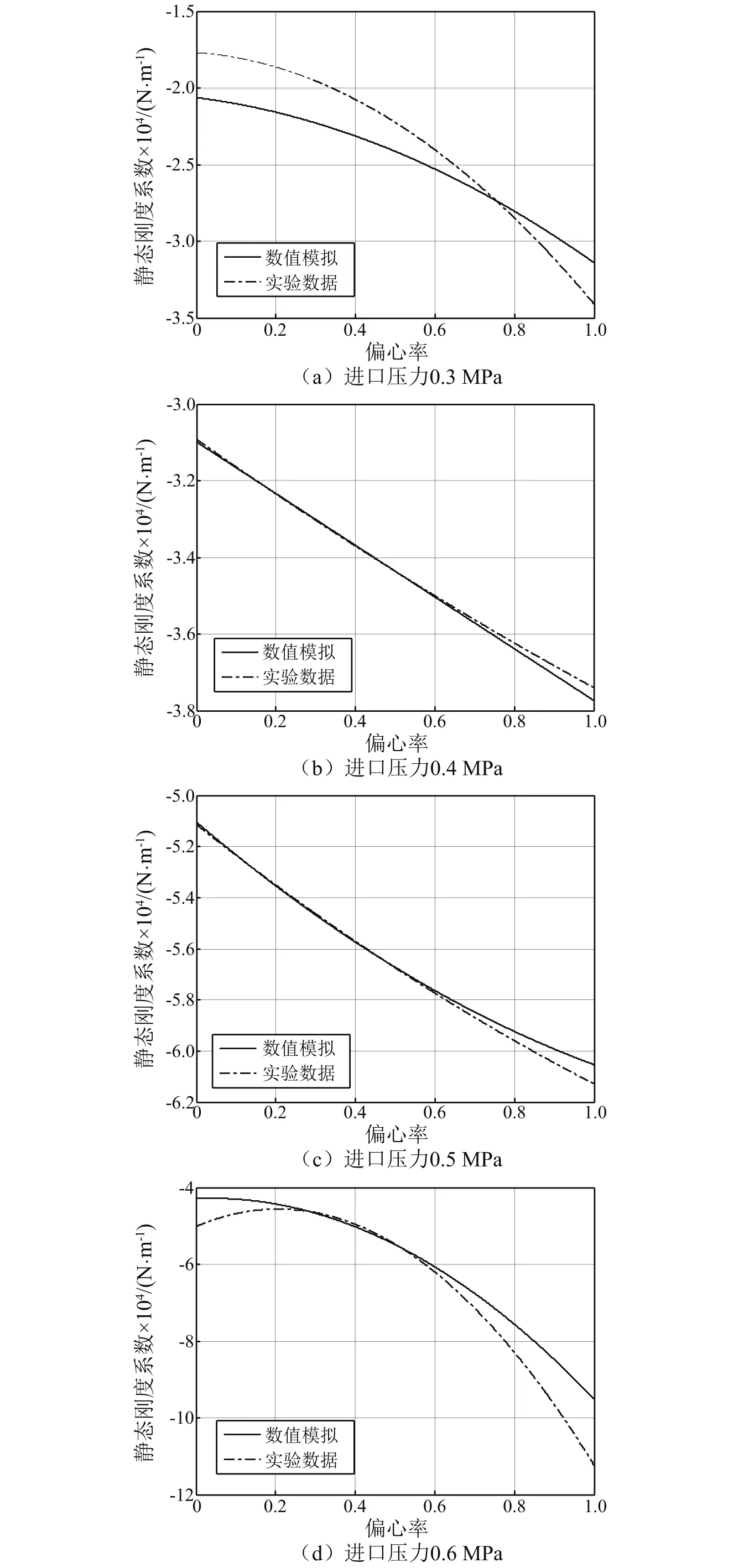
图10 不同进口压力下静态刚度系数理论与实验对比Fig.10 Theoretical and experimental comparison of static stiffness coefficients under different inlet pressures
3.3 静态稳定性分析
为了分析密封静态不稳定性机理,本文进一步通过数值方法研究了密封腔内压力及马赫数分布情况。图11给出了不同偏心状态下密封最大和最小间隙压力差沿泄漏方向分布情况。可以看出:①最大间隙与最小间隙的压力之差基本都为正值,即会产生一个使转子偏离静子几何中心的气流力;②随着偏心程度和进口压力的增大,压力差值也在增大。上述压力差值最终导致密封产生负的静态刚度。
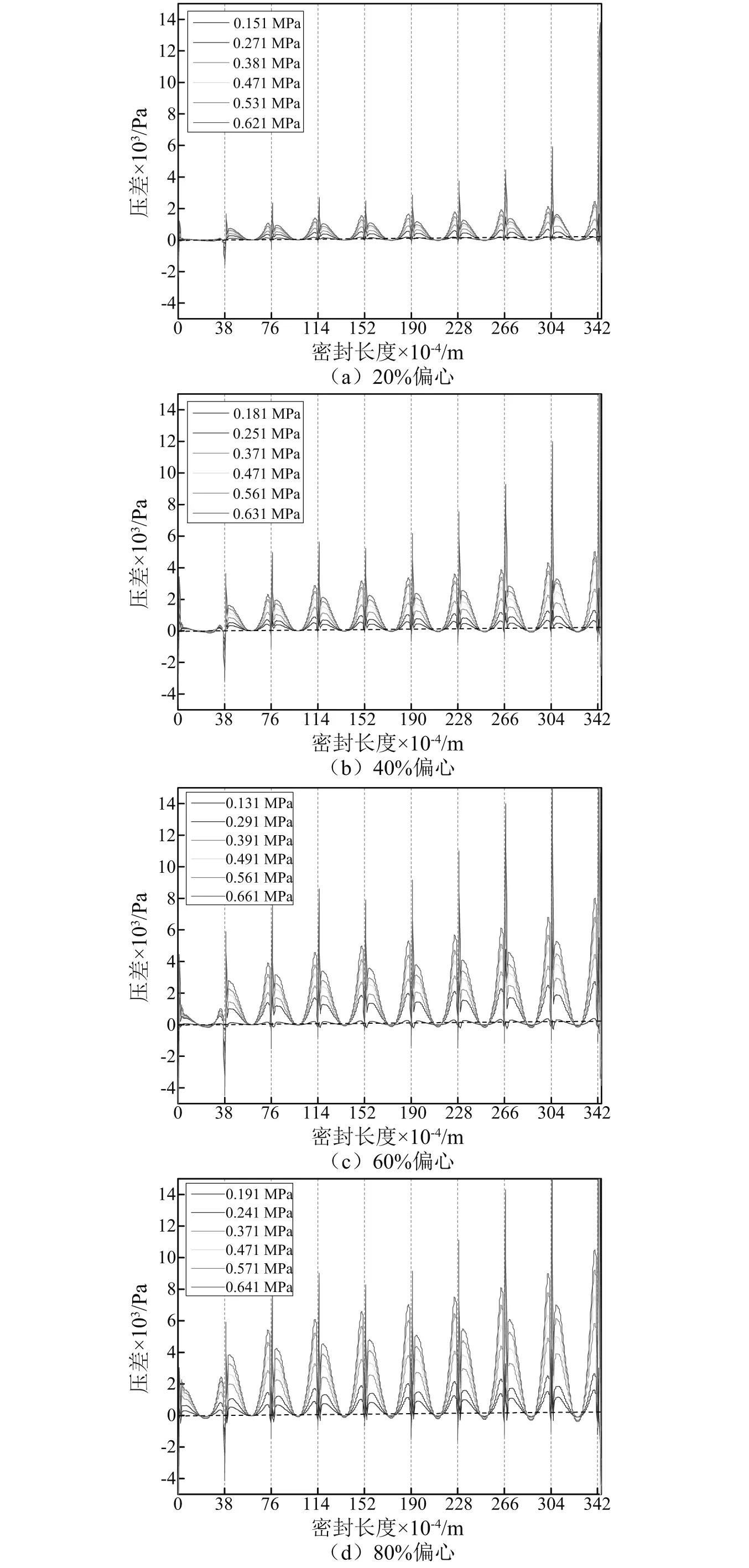
图11 不同偏心条件下最大和最小间隙压力差沿轴向分布Fig.11 The maximum and minimum clearance pressure difference along the axial distribution under different eccentric conditions
为分析产生负刚度的原因,对密封最大和最小间隙气流的马赫数进行了研究,结果如图12所示。
图12给出了不同偏心状态下最大和最小间隙马赫数沿密封长度分布情况。大间隙气流速度较大大,
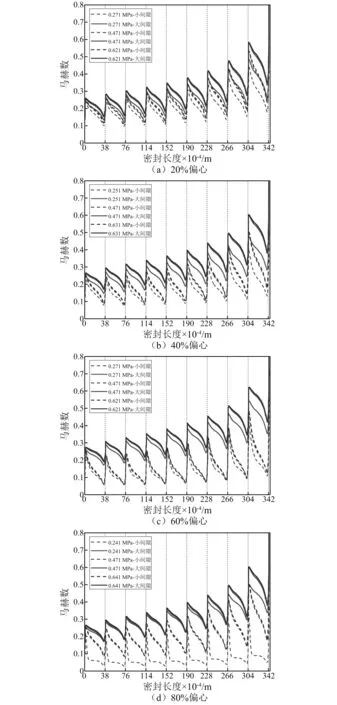
图12 不同偏心下最大和最小间隙马赫数沿密封长度变化Fig.12 Variations of maximum and minimum clearance Mach numbers along the seal length under different eccentricities
且随着偏心程度的增大,大间隙和小间隙的速度差值也会增大。根据传统Lomakin效应理论,会产生正的刚度,与本文结论相悖。然而,本文所研究的梳齿密封小间隙的轴向速度较小,但是在小间隙齿顶间隙处(即对应图中竖直虚线处)速度增加幅度要大于大间隙齿顶间隙,惯性效应占主导,质量惯性力显著增大,压力能降低,从而导致大间隙压力大于小间隙,产生使转子偏离中心的气流力及负刚度,最终导致出现静态不稳定现象。
4 结 论
对梳齿密封静态稳定性开展了理论与实验研究。以透平机械流体激振实验台为基础测试密封气流力及静态刚度系数,并建立密封三维数值分析模型,对比分析理论与实验结果。
(1) 实验研究发现,实验密封内会产生加剧转子偏心的静态气流力,密封静态刚度系数为负值,产生静态不稳定现象。
(2) 数值结果表明,不同偏心状态下密封最大和最小间隙压力差基本都为正值,即会产生一个使转子偏离静子几何中心的气流力。随着偏心程度和进口压力的增大,压力差值也在增大,上述压力差值最终导致密封产生负的静态刚度。理论和实验结果相吻合,随偏心程度和进口压力的增大,气流力和静态刚度系数也不断增大,静态刚度系数约为-120~-15 kN/m。
(3) 密封静态不稳定现象主要是由于密封小间隙速度沿密封泄漏方向增加较快,质量惯性力显著增大,压力能降低,从而导致大间隙压力大于小间隙,产生使转子偏离中心的气流力及负刚度。

