基于拟态物理学优化算法的船舶变速避碰决策
于家根, 刘正江, 卜仁祥, 高孝日, 李伟峰
(大连海事大学 航海学院, 辽宁 大连 116026)
船舶在狭窄水域内航行,交通密度加大,会遇局面复杂,使得操纵船舶难度增加,船舶避碰更加困难,一旦决策失误将会导致事故发生。蚁群算法、粒子群算法和人工鱼群算法等群集智能优化算法在船舶避碰决策中已有研究,并取得一些成果[1-3],这些研究以转向避碰决策为主,但在狭窄水域中转向受限情况则不适用。船舶高速化、大型化发展使得船舶在狭窄水域内驶离航向能力受到限制,变速避碰措施更为有效。
拟态物理学优化[4-6](Artificial Physics Optimization,APO)算法是一种基于种群的启发式随机搜索算法,具有种群多样性好、搜索效率高的优点。针对狭窄水域内船舶变速避碰决策问题,考虑《国际海上避碰规则》(以下简称《规则》)的约束,运用APO获取可行解范围内的最佳变速避碰决策值。
1 问题描述
《规则》第12~15条、第18~19条规定了船舶避碰责任,本文的研究对象为机动船,第12条帆船条款暂不考虑。其中:第13~15条和第18条,属于互见中的行动条款,本船应根据相关条款确定避碰责任(让路/直航/避让责任);第19条属于能见度不良时的行动条款,本船与目标船存在碰撞危险时,本船均负避碰责任且需采取行动。
船舶在狭窄水域中航行,存在碰撞危险时,由于水域受限本船选取变速行动避免碰撞。在采取变速避碰行动时,减速避碰是常见的方法,考虑《规则》第8条避碰行动“大幅度”的要求,减速避碰要求速度至少下降1/2。[7]此外,速度值不能低于船舶的维持舵效的最小速度(紧急情况除外)。所以,《规则》约束了变速行动速度值的范围。
本船采取的变速避碰行动要考虑变速后的碰撞危险度和变速的能量损失,即船舶变速避碰的目标评价。借鉴APO算法的寻找最优解过程,可将船舶变速避碰决策问题抽象为:在限定的可行解空间中,获取基于避碰目标函数的最佳船舶速度值问题。变速避碰决策与APO算法的对比见表1。
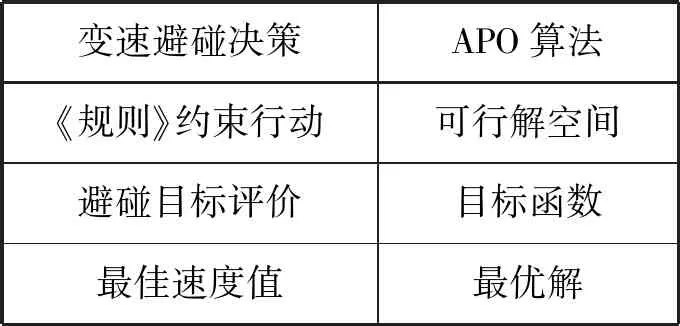
表1 变速避碰决策与APO算法的对比
2 目标函数的建立
船舶变速避碰需要考虑船舶变速后碰撞危险度和船舶变速能量损失两个要素。为此,分别建立碰撞危险度函数f1和变速能量损失函数f2,重点考虑碰撞危险度的影响,变速避碰的总目标函数为
f(xj)=0.8f1(xj)+0.2f2(xj)
(1)
式(1)中:xj为APO算法的种群中个体j的船舶速度值。
2.1 碰撞危险度函数
衡量船舶变速后的碰撞危险度,本船与各目标船的最近会遇距离(Distance to Closest Point of Approach,dCPA)是重要参数。其表达式为
dCPA=fDCPA(vo,Co,vt,Ct,dt,TB)
(2)
式(2)中:dCPA的值可通过本船航速vo、本船航向Co、目标船航速vt、目标船航向Ct、目标船距离dt和目标船真方位TB确定。
船舶减速至预定速度,需要一定冲程ds和冲时ts后才可降速至预定速度,与各目标船的dCPA值受ds和ts的影响。本船保持航向并采取减速避碰行动,目标在船保向、保速、减速过程中,目标船的dCPA是持续变化的,待减速至预定速度voN,dCPA则不再发生变化,获得这一时刻目标船相对本船的位置(xts,yts),便可得到目标船新的距离dtN和新的方位TBN,减速后的dCPA值可通过dCPAN=fDCPA(voN,Co,vt,Ct,dtN,TBN)求得。本船的速度稳定后的目标船的位置见图1,可用式(3)和式(4)求取,目标船新的距离和方位可由式(5)和式(6)求取。
(5)
(6)
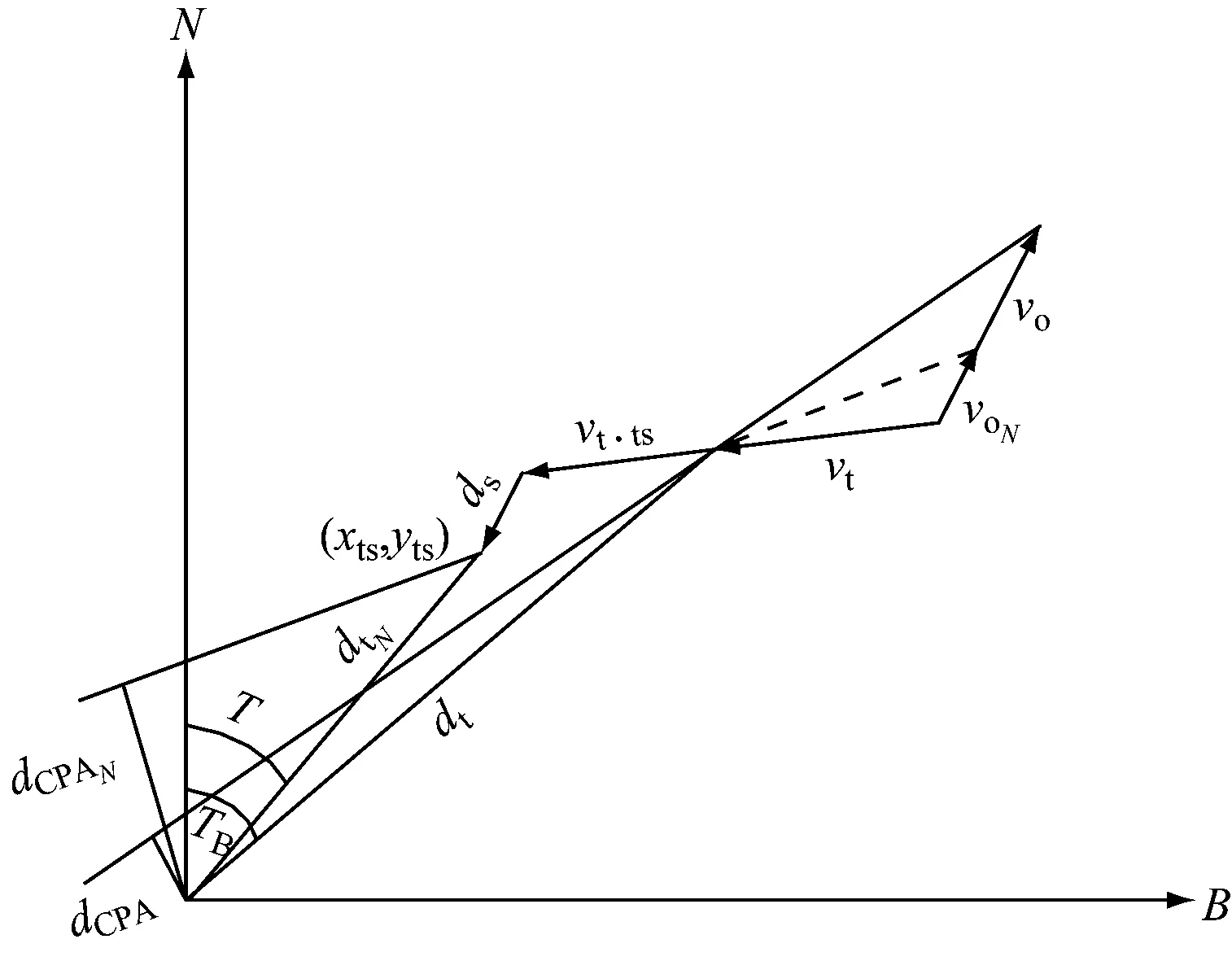
图1 相对运动模式dCPAN求取模型
船舶变速后,本船与各目标船的最小的dCPA值越大,则越安全,即碰撞危险度越小。因此,碰撞危险度函数f1选取为
(7)
式(7)中:f1(xj)的值域为(0,1];dCPAjk为个体j与第k个目标船的dCPA值;N为目标船的数目。
2.2 变速能量损失函数
本船减速避碰行动受《规则》的约束,船舶速度范围应为在维持舵效的最小速度vse和初始速度vo的1/2之间,即船舶减速避碰的可行解空间为[vse,vo/2]。船舶减速越大则船舶能量损失越大,且恢复航速时船舶的能耗也大。因此,船舶降速后的速度在限定范围内尽可能取大,变速能量损失函数f2取为
f2(xj)=(xj-vo/2)/(vse-vo/2),xj∈[vse,vo/2]
(8)
式(8)中:vse为本船的维持舵效的最小速度;vo为本船的初始速度;f2(xj)的值域在[0,1],其值越小xj值越大。
3 基于APO算法的变速避碰决策
APO算法[8-10]中,个体具有质量、位置和速度等属性。算法在个体之间引入吸引和排斥规则,即适应值(目标函数值)好的个体吸引差的个体,适应值差的个体排斥好的个体,适应值最好的个体则不受影响。适应值越好的个体质量大、虚拟作用力越大。利用这种虚拟力作用规则迭代进化,以获取最优个体。
3.1 初始化种群
设种群数目为Npop,Mmaxiter为最大迭代代数,xj(t)为种群中个体j(j∈[1,2,…,Npop])在第t代的位置,即变速避碰决策中的船舶速度值。设vj(t)表示个体j在第t代的速度,即个体位置更新的步长。个体位置xj(t)的约束范围为[vse,vo/2],速度vj(t)的约束范围为[vmin,vmax],随机初始化种群。计算个体的适应值,选出最优个体(最佳船舶速度值)和其适应值。
3.2 个体位置更新
按式(9)计算个体的质量为
(9)
式(9)中:f(xbest)为第t代内最优个体的适应值;f(xworst)为最差个体的适应值。
按式(10)和式(11)计算个体所受虚拟力合力。
(10)
(11)
式(10)中:Fjk为个体k对个体j的虚拟作用力;rjk=xk-xj为个体j到个体k的距离;G为引力常数,取0.1;Fj为个体j所受的虚拟力合力。
个体j按式(12)进行位置更新,最优个体不受影响,直接传递至下一代。
vj(t+1)=wvj(t)+aFj/mj
xj(t+1)=xj(t)+vj(t+1), ∀j≠best
(12)
式(12)中:a~N(0,1)为服从(0,1)正态分布的随机变量;w为惯性权重,w∈(0,1),其值按w=0.9-(t-1)/Mmaxiter×0.5计算。
3.3 决策流程图
基于APO算法的船舶变速避碰决策流程见图2。
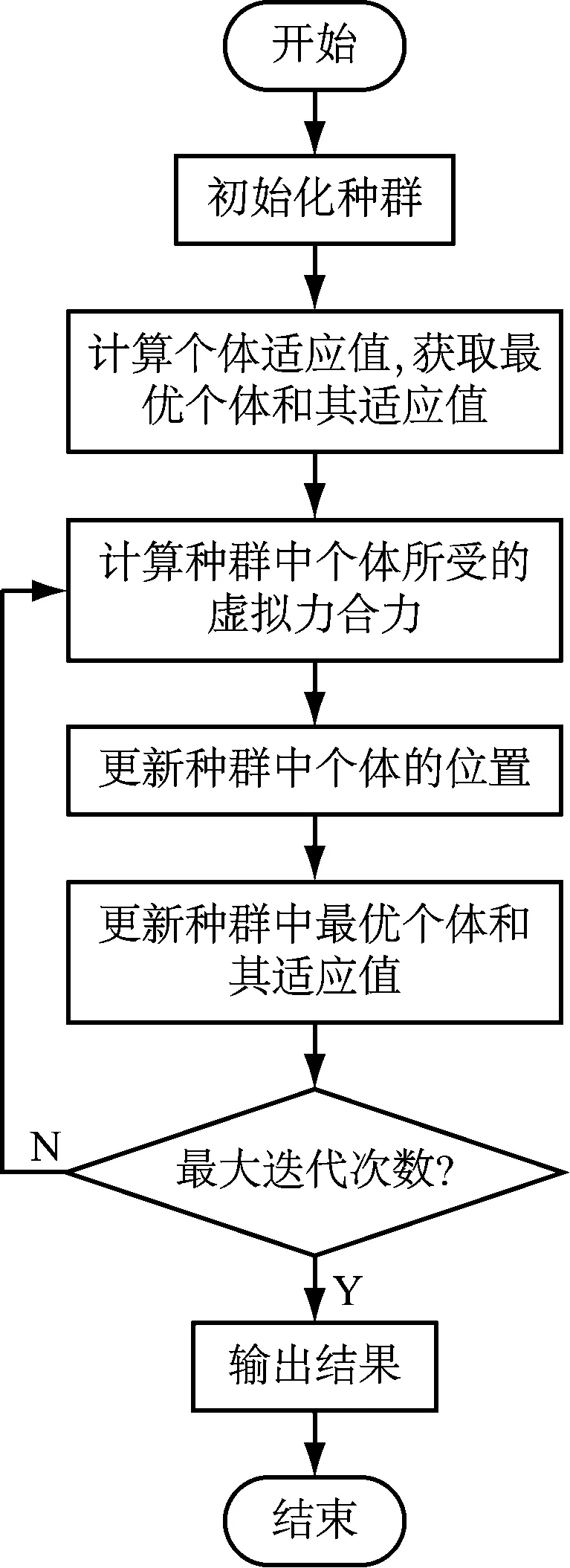
图2 基于APO算法的决策流程
4 仿真实例分析
为验证决策方法的可行性和有效性,研究选取狭窄水域内多船会遇的案例,基于MATLAB平台进行仿真并分析结果。
4.1 仿真实例
某狭窄水域内航行,能见度不良,本船(OS)船长L为140 m,载重吨=10 000 t,航向Co=000°,航速vo=15 kn,维持舵效的最小速度vse=2 kn。同时会遇5艘船舶(编号TS1~TS5),且不在互见中,会遇局势见图3,雷达标绘获得目标船的数据见表2。表2中:dCPA正值表示目标船过艏部,负值过艉部。
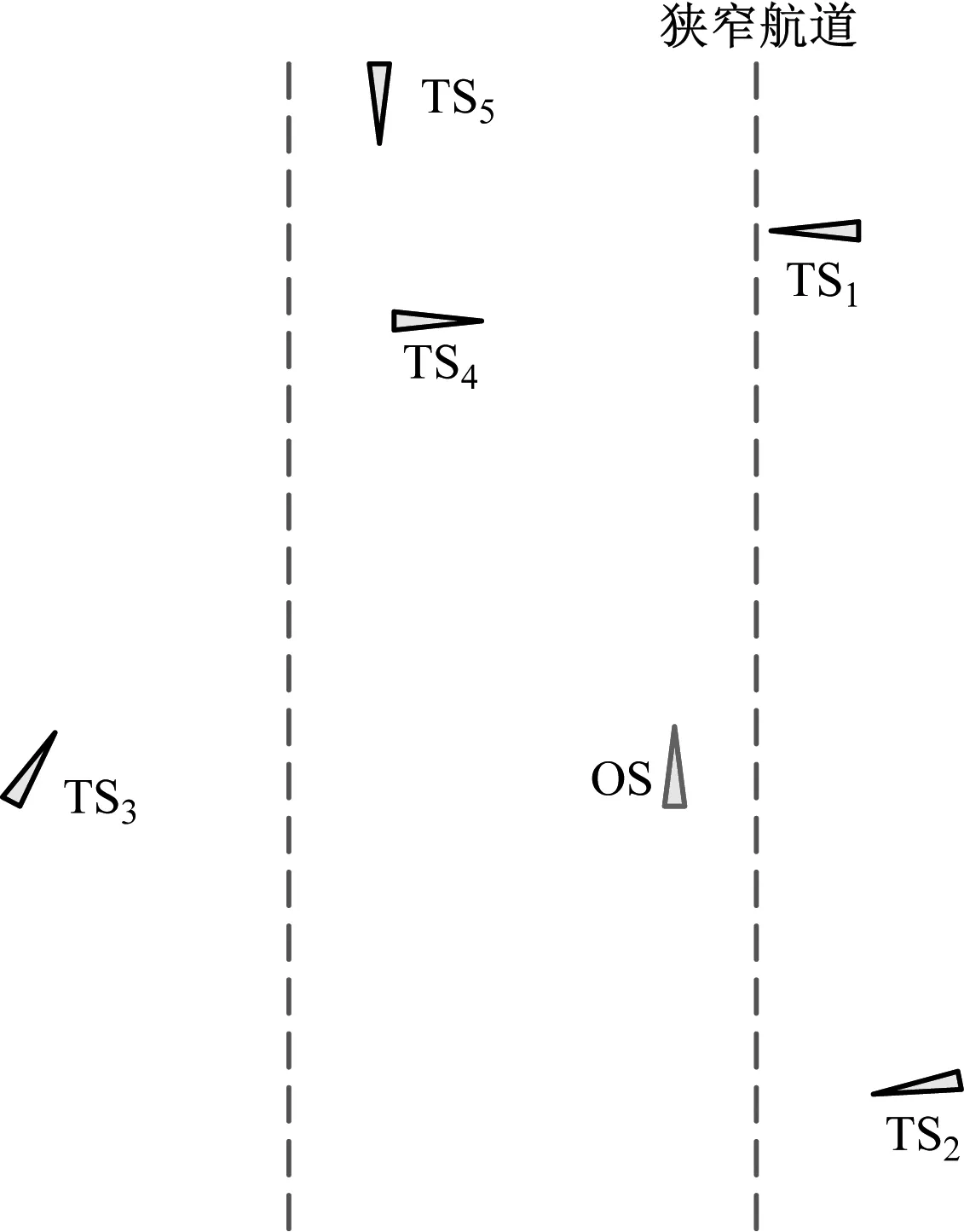
图3 会遇局势

表2 目标船的数据
安全会遇距离(Safe Distance,ds)设为1 n mile,本船与TS1、TS3和TS4的会遇距离小于ds,存在碰撞危险,按《规则》第19条要求需要采取避碰行动,本船采用倒车减速避碰方式。
万吨船全速倒车停船冲程为6~8L,船舶减速常数约为4 min。[11]为简化问题,设本船倒车减速冲程ds=(vo-xj)0.6L;本船倒车减速冲ts=(vo-xj)0.5。种群数目Npop设为30,最大迭代代数Mmaxiter设为2 500,步长约束[vmin,vmax]设为[-0.1,0.1],个体位置(船舶速度)约束设为[vse,vo/2],即[2.0,7.5]。
4.2 结果分析
运行算例30次,获取最优个体值xbest及最优个体适应值fbest,各次运行结果见表3。分析运行结果可知:最优个体值(最佳船舶速度值)的区间为[6.397 2,6.409 0],最优个体适应值的区间为[0.412 6,0.418 3],按船速读取习惯保留一位小数,最佳船速值收敛于6.4 kn,最优个体适应值收敛于0.4。这说明算法收敛、有效。
仿真的迭代过程见图4和图5。图4为各次迭代的最优个体值,即最佳航速值。各次迭代的最优个体适应值见图5。
经过仿真实例得出结果:最佳船速值为6.4 kn。船舶从15 kn减速至6.4 kn,倒车减速冲程为0.39 n mile,冲时为4.3 min,稳定至6.4 kn后与各目标船的dCPA值为[1.70,-2.04,2.91,1.12,-1.74]。目标船TS1、TS3和TS4的dCPA>ds,从艏部安全通过,目标船TS2和TS5的|dCPA|>ds,未新增危险,从艉部安全通过。减速避碰决策有效、可行,能安全避让所有目标。
5 结束语

表3 运行结果

图4 迭代进化图(最优个体值)

图5 迭代进化图(最优个体适应值)
针对狭窄水域内船舶的避碰决策问题,提出一种基于拟态物理学优化算法的船舶变速避碰决策方法。根据《规则》的要求和船舶自身的操纵性能,限定变速决策值的范围,作为APO算法的可行解空间。用碰撞危险度和变速能量损失评价决策的优劣,以侧重安全为原则,建立船舶变速避碰的目标函数,并将其作为APO算法适应度。由于减速需要过程,方法中考虑了减速冲程和冲时对避碰的影响。本研究引入避碰案例,基于MATLAB平台进行仿真,利用APO算法的全局快速寻优能力,获得最佳船舶速度值,避碰决策可行、有效。后续研究的重点将放在转向和变速结合避碰决策上。

