兰州新区保障住宅装配式钢结构的抗震性能分析

李晓飞 薛晓峰 吴彦霖

(甘肃农业大学 兰州730010)

引言

随着我国城市化进程的迅速发展，城市住宅的需求量正在与日俱增，相对于目前广泛应用的现浇混凝土结构建筑，装配式结构建筑具有诸多显著优点。与普通现浇结构相比，装配式建筑的标准化、工业化程度更高。我国地震频发，近年来数次强烈地震给人类造成了巨大的生命财产损失[1]。基于强度的抗震设计方法已经不能满足要求，基于性能的抗震设计[2，3]越来越受到工程师的重视。

目前，国内外学者对不同形式的非装配式钢结构pushover 分析的工作做的相对较多。2008年，孙爱伏、欧进萍学者对高层钢结构pushover分析的侧向力分布模式进行了研究，给出高层钢结构 pushover 分析的合理化建议；2011年，何文滔等学者对高耸钢结构模型进行了小震、中震和大震作用下的振动台试验分析，通过此分析验证 pushover 分析的可靠性；2014年，王金祥等学者对一幢6 层钢框架在四种工况作用下的静力弹塑性性能进行分析研究，认为pushover分析是目前钢结构在罕遇地震下进行弹塑性分析的有效方法。然而，对装配式钢结构尚缺乏抗震性能的了解。本文对兰州新区装配式钢结构保障性住宅1#楼进行了罕遇地震作用下的静力弹塑性分析，来了解此结构在罕遇地震下的性能。

1 工程概况

此结构为装配式钢结构，共 10 层。1～2 层层高为3150mm、3～10 层层高为2900mm，出屋面层(11 层)层高为2900mm。图1为结构平面图。梁截面为 H 型钢梁，采用 Q345 钢。柱截面为方钢管混凝土柱，采用Q345 钢和C40 混凝土。内墙体采用水泥基复合夹芯墙板，外围护墙体材料采用砂加气。梁、柱截面见表1。兰州新区设防烈度为7 度、设计基本地震加速度为0.15g、场地类别为Ⅱ类场地、特征周期为0.45s。

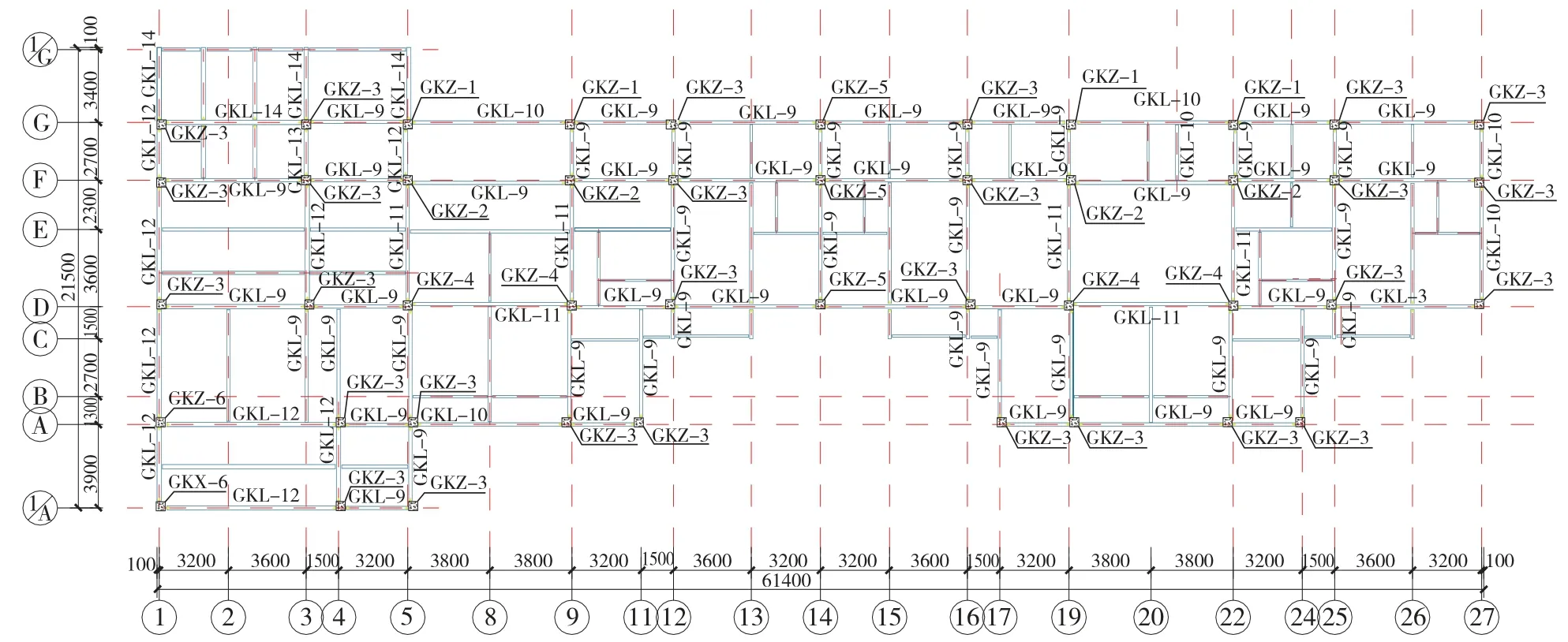
图1 结构平面图Fig.1 Planer view of structure

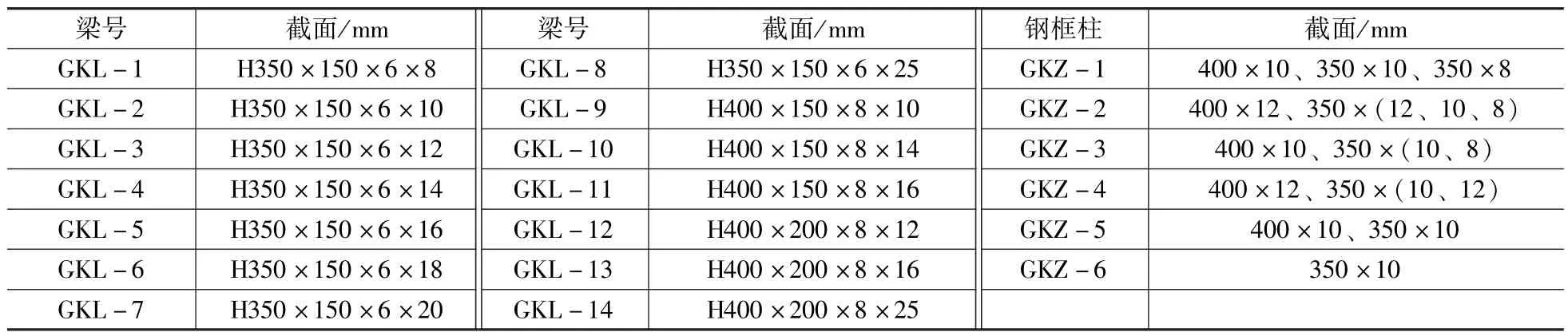
表1 梁柱截面尺寸Tab.1 Section dimensions of beam and column

2 Pushover分析

Pushover分析方法[4-6]，也称为静力弹塑性分析方法，是一种基于性能评估已建结构和设计新结构的方法。Pushover方法是指对建筑结构模型沿结构高度方向施加一定的侧向力或一定的侧向位移[7，8]，直到建筑结构模型的目标控制点达到目标位移或建筑结构破坏为止。因为这种方法在静力加载状态下对结构进行弹塑性分析，所以本质上还是一种静力分析方法。首先，应明确使用pushover分析的目的是对建筑结构的抗震性能进行检查或评估，目标是预测结构和构件在给定地震作用下的峰值响应。分析过程中得到结构的基底剪力和顶点位移关系曲线，即结构的能力曲线，结构的能力曲线与地震需求曲线的交点，即为性能点，见图2。通过结构的荷载-位移曲线(能力曲线)来描述在侧向力作用下，结构变形从弹性到弹塑性发展的不同阶段。荷载-位移曲线上的不同位置代表不同的性能控制点，通过在给定荷载作用下结构的期望性能点所在的位置，来判断结构的抗震能力是否达到要求。因而，pushover分析可以考虑结构在设计地震作用下的非线性行为，明确结构中的薄弱部位，预测构件能力需求，从而更好地理解结构行为，采用更合理的而非保守的抗震性能目标。

图2 结构性能点Fig.2 Target performance of the structure

经过pushover分析以后，利用所得到的性能点以及性能点对应结构控制点的位移，通过3个方面对结构的抗震性能进行评估：

(1)顶点位移。观察结构的弹塑性顶点位移是否满足《建筑抗震设计规范》(GB 50011—2010)[10](以下简称《抗规》)的要求。

(2)层间位移角。观察结构的弹塑性层间位移角是否满足《抗规》要求。

(3)出铰机制。观察梁柱构件的弹塑性铰变形是否超过了某一性能水准下的变形要求和出铰的顺序。

2.1 模型建立

采用SAP2000软件建模、计算和分析[9]，此结构是装配式建筑结构，根据装配式结构的施工工艺和施工过程形成节点的受力与非装配式结构有一定差别，根据项目图纸显示的梁、柱节点性质建立模型节点，SAP2000为框架单元提供了弯矩铰、剪力铰、轴力铰和压弯铰，可以在框架梁柱单元的任意部位布置一种或多种塑性铰。各种塑性铰的本构模型如图3所示。图中纵坐标表示弯矩、轴力、剪力，横坐标表示曲率或转角、轴压变形、剪切变形。整个曲线分为四个阶段：弹性阶段(AB)、强化段(BC)、卸载段(CD)和塑性段(DE)。SAP2000提供了两种定义塑性铰的方法：一种是用户自定义塑性铰的属性；另一种是程序按照美国规范FEAM273和ATC-40方法来定义塑性铰的本构关系，塑性铰应设置在弹性阶段内力最大处，因为结构的这些位置最先达到屈服。对于梁单元，一般情况是两端内力最大，并且主要承受弯矩荷载，所以在梁的两端设置弯矩铰(M)，而柱承受轴力和弯矩的共同作用，故柱两端设置压弯铰(PMM)。结构的三维有限元模型见图4。

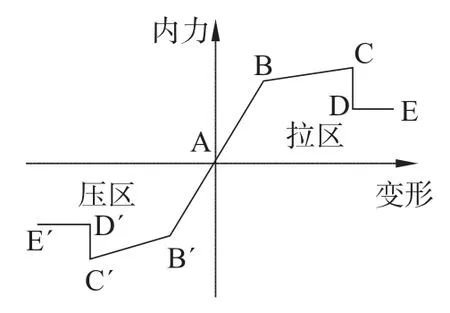
图3 塑性铰的本构模型Fig.3 Constitutivemodel of plastic hinge

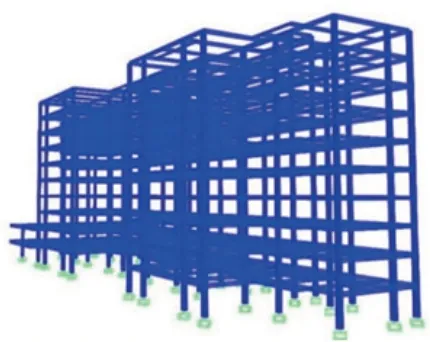
图4 结构有限元模型Fig.4 Finite element model of structure

2.2 目标位移和地震系数

由《抗规》可知，框架结构的弹塑性结构层间位移角限值为1/50，本次计算取结构顶层的最高节点(343号节点)的水平位移作为位移限值，位移限值为(1/50)×29.5m=0.59m，实际的目标位移可由结构的性能点求出。根据工程经验，一般认为当结构的相对顶点位移达到目标位移时，结构构件和非结构构件趋于破坏，可以此作为pushover分析破坏标志。

根据ATC-40[11]中关于性能点的确定方法，结合《抗规》中的弹性反应谱，可求得结构在小震、中震、大震下对应的性能点的位置，具体性能点确定方法是确定需求谱曲线参数Ca与Cv。

由于程序中Ca与Cv的确定是依据美国的场地地理条件确定的，根据我国规范与美国规范的对比，可以得出Ca、Cv与抗震规范反应谱之间的转换关系如下：

当0.1s＜T≤Tg时

当Tg＜T≤5Tg时

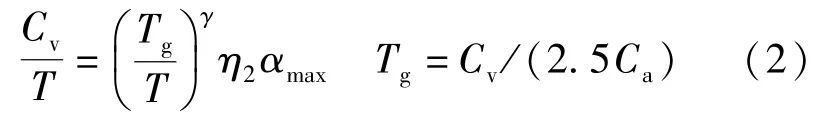
当5Tg＜T≤6s时

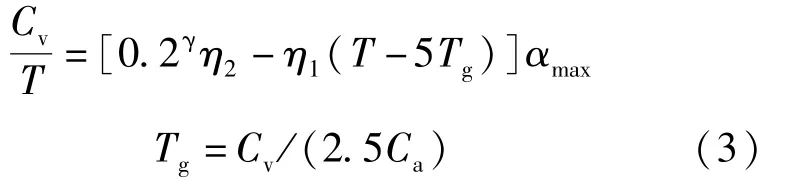
式中：Ca为地表有效峰值加速度；Cv为阻尼0.05时对应的系统速度反应谱；αmax为地震影响系数最大值；Tg为特征周期；T为结构自振周期；η1为直线下降段的下降斜率调整系数；η2为阻尼调整系数；γ为衰减指数。依据公式(2)以及地震参数，7度罕遇地震作用下，结构自振周期T=0.72s，算出Ca=0.276，Cv=0.31。

2.3 加载方式

通过对结构施加侧向荷载，能大体上真实反映出地震作用下结构的位移状况。而由于任何一种荷载分布形式都不能全部反应结构全部的变形和受力要求，因此，在对结构进行弹塑性分析(pushover分析)时，需要至少用两种以上的侧向加载模式。采用均匀分布荷载加载模式和倒三角荷载加载模式。

在SAP2000中，均匀分布荷载侧向力是用均一的加速度和响应质量分布的乘积获得的；倒三角分布荷载侧向力实用第一振型和第一振型下的固有频率的平方及相应质量分布的乘积获得的。

3 结果分析

3.1 基底剪力-顶点位移

图5、图6为两种加载模式下的pushover 曲线，从图中可以看出，达到性能点时，两种加载模式的基底剪力和位移有一定的差值，均布荷载作用下的基底剪力比倒三角荷载作用下的基底剪力增加了35%，倒三角荷载下的位移比均布荷载作用下的位移增加了33%。

图5 倒三角加载模式pushover 曲线Fig.5 Pushover curve of inverted triangular loadingmode

当侧向加载模式为倒三角形加载模式时，结构的底部最大承载力为2014.784kN，顶点位移为 88mm，88mm ＜ 29500 × 2% = 590mm(2% 是《抗规》规定的弹塑性层间位移角限值)，所以控制点位移满足弹塑性极限要求。当侧向加载模式为均匀分布力加载模式时，结构的底部最大承载力为 2724.129kN，顶点位移为 66mm，66mm ＜29500 ×2% =590mm，所以控制点位移也满足弹塑性极限要求，说明结构能够抵抗相应烈度地震作用，否则说明结构的抗震能力不足。

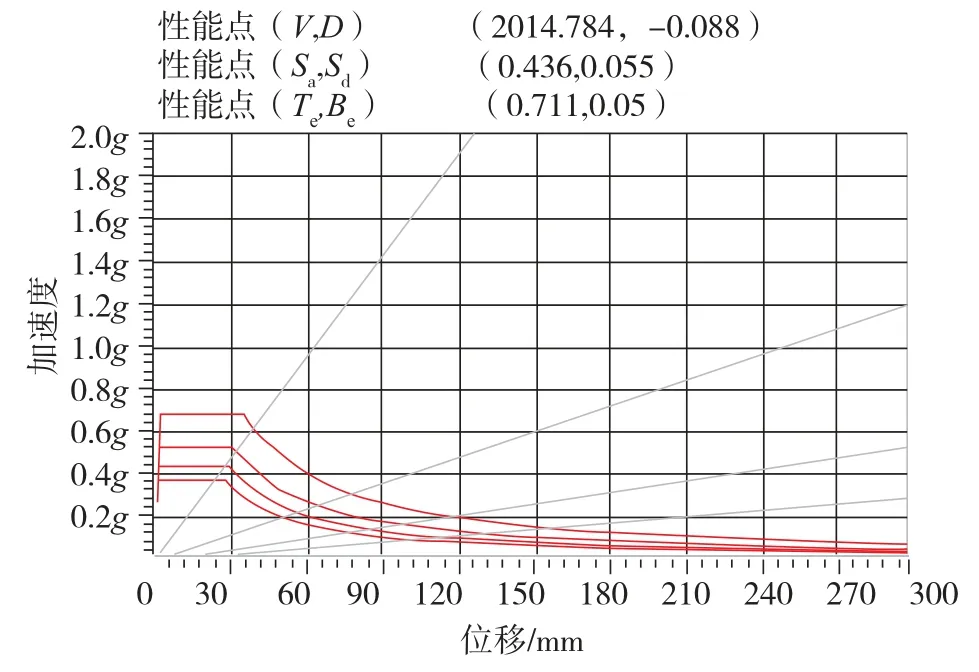
图6 均匀分布荷载加载模式pushover 曲线Fig.6 Pushover curve of uniformly distributed loadingmode

3.2 层间位移角

表2为性能点处框架(图7)在两种加载模式下的楼层位移和层间位移角。图8为结构的层间位移沿高度分布的情况，从图8可以看出，倒三角加载模式下的楼层位移除了1 层外，其余各层的位移均大于在均匀分布加载模式下的位移，两种加载模式下的楼层位移均满足规范要求，图9为结构的层间位移角沿高度分布情况，从图9可以看出，倒三角加载模式下的层间位移角除了1 层外，其余各层的位移均大于在均匀分布加载模式下的位移，说明结构的第四层是薄弱层。而均匀分布加载荷载下，在第三层出现拐点，故第三层是薄弱层。

表2 各楼层位移和层间位移角Tab.2 Floor displacement and inter-story displacement angles

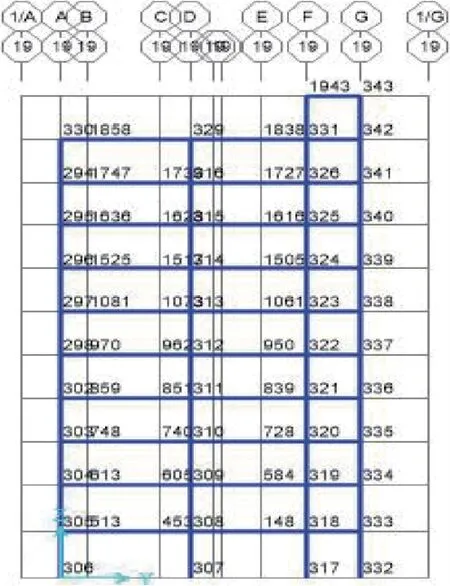
图7 性能点处19 榀框架节点号Fig.7 Framework at performance point

图8 性能点处楼层位移Fig.8 Floor displacement at performance point

图9 性能点处层间位移角Fig.9 Interlayer displacement angle at performance point

3.3 出铰机制

分析出铰机制，以性能点处框架为研究对象。图10为此处框架的单元号详图。倒三角加载模式下结构达到性能点时是pushover 第15 步，达到性能点后的出铰顺序和分布见图11。均匀分布加载模式下结构达到性能点时是pushover 第12步，达到性能点后的出铰顺序和分布见图12。

由图11、图12可知，两种加载模式下的出铰顺序和出铰数量有一些差别，但相同点则是都在F-G 跨内先出铰，倒三角加载模式出铰的数量多于均匀分布加载模式下的出铰数量，除了首层柱脚均屈服之外，其余的柱并未形成塑性铰，塑性铰分布在梁两端，符合“强柱弱梁”的设计。倒三角加载模式下，单元 522、967、1106 两端塑性铰达到 IO 与 LS 之间，单元 670、828 两端的塑性铰状态达到LS 与CP 之间，其余塑性铰均在B 与 IO 之间；在均布加载模式下，单元 967 两端的塑性铰达到 IO 与 LS 之间，单元 522、670、828 两端的塑性铰状态发展到LS 与CP 之间，而其余塑性铰均在B 与IO 之间。由出铰顺序可知，框架的薄弱部位在1 到5 层的F-G 跨。

在不同侧向加载模式下结构的弹塑性静力pushover 分析结果从能力曲线到出铰机制上均有一定的不同，因此，为了对结构的抗震性能有全面的了解，建议最少用两种以上的侧向荷载加载分布模式对结构进行弹塑性静力分析。

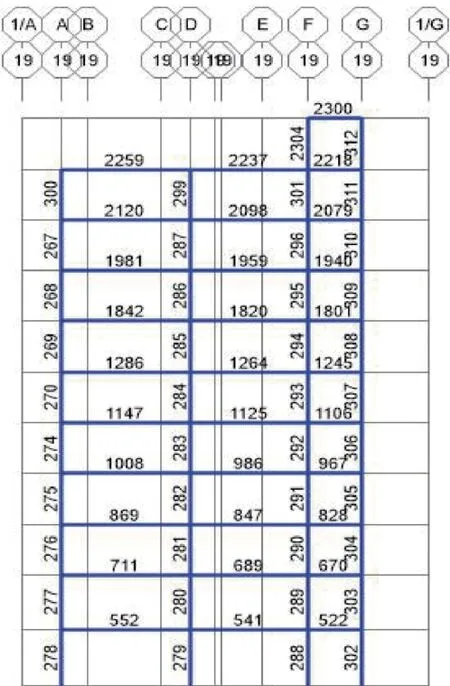
图10 性能点处框架单元号Fig.10 Frame unit number at performance point

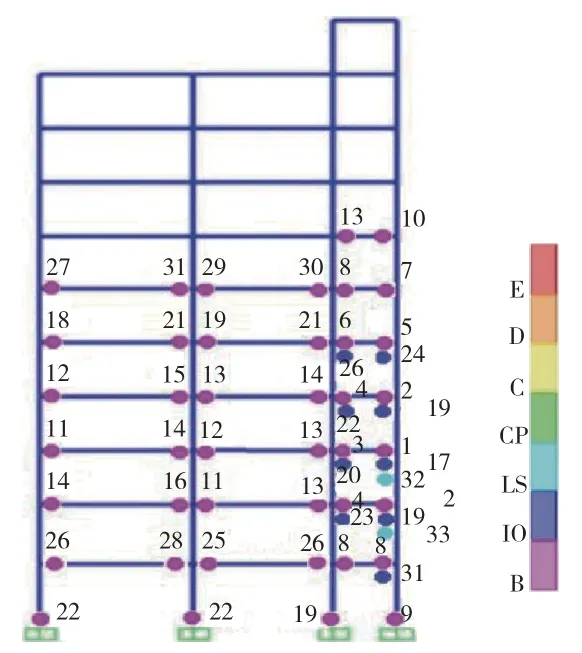
图11 倒三角加载模式塑性铰分布Fig.11 Distribution of plastic hinge in inverted triangular loadingmode

图12 均匀分布加载模式塑性铰分布Fig.12 Distribution of plastic hinge in uniformly distributed loadingmode

4 结论

1.结构在两种侧向加载模式下的控制点位移和层间位移角均满足《建筑抗震设计规范》(GB 50011—2010)中罕遇地震下弹塑性限值要求，说明结构能够抵抗罕遇地震的作用；

2.从两种侧向荷载加载模式得到的出铰机制可以看出，除了首层柱底出现塑性铰之外，其余柱没有出现塑性铰，因此，满足“强柱弱梁”的设计。