一道高考题的解题探究与价值挖掘

上海向明中学(200020) 侯宝坤

每年的高考题都会出现一些构思巧妙,重点突出,方法多样的试题,这些试题引起了广大教师的探究热情.笔者以上海选择的压轴题为例谈谈这方面的体会.

题目(2019年高考上海卷第16 题)已知tanα·tanβ=tan(α+β),有下列两个结论：①存在α在第一象限,β在第三象限；②存在α在第二象限,β在第四象限；则( )

A.①②均正确 B.①②均错误 C.①对②错 D.①错②对

一、考生的思维障碍

高考结束后,笔者做了简单的访谈,选对这道题的学生占80%左右,似乎压轴的分量不够,这是因为上海学生可以用计算器检验的缘故,访谈的学生中有学生做了简单推算,但都铩羽而归,没有以代数运算和逻辑推理准确分析得出答案来,说明学生并不懂这一题涉及的知识和方法.对学生遇到的思维障碍现扼要呈现如下：

情形1时,左边为正,且α+β ∈(π,2π),所以右边也可以取到正值,所以①对,同样②也对,选A.

情形2式子变形为：tanαtanβ(1-tanαtanβ)=tanα+tanβ,也估计tanα、tanβ都可能是正的,同样选了A.

情形3认为α,β是对称的,①②要么都对要么都错,代了一个tanα=1 发现无解,所以①②都错,选B.

情形4转化为：tan2αtan2β+(1-tanα)tanβ+tanα=0,发现无法分解因式就放弃了,或者发现Δ=(1-tanα)2-4 tan3α ≥0 不会解! 然后就计算器了.

二、考题的解法探究

可以明显的感受到,学生没有用函数来处理方程和不等式解的意识,首先提供一个基于学生思路的一个求导的方法.

方法1 将原方程转化为：tanαtanβ(1-tanαtanβ)=tanα+tanβ,

Δ=(1-tanα)2-4 tan3α ≥0,令t=tanα,则Δ=f(t)=-4t3+t2-2t+1,t ∈R,由f′(t)=-12t2+2t-2＜0 恒成立知f(t)为减函数,又,0,f(t0)=0,所以所以,只有当tanα≤t0时,关于tanβ的方程(∗)有解.若0＜tanα≤t0＜时,由知,tanβ1＜0,tanβ2＜0,此时α可以在一、三象限,β只能在二、四象限,所以结论①是错误的.若tanα＜0 时,由tanβ1tanβ2=＜0知,tanβ1＜0,tanβ2＞0,此时α在二、四象限,β可以在所有象限,所以结论②是正确的.因此,正确答案为D.

由于上海学生不学导数,那么不用导数是否可行呢? 其实完全可以用单调性的定义来分析这个函数.

方法2∀t1,t2∈R,且t1＜t2,

后面处理如同方法1,不再赘述.

能不能利用和、差、复合将陌生函数转化成熟悉的函数呢?

方法3 将f(t)分拆成-4t3和t2-2t+1 时,t≤1 都为减函数,所以f(t)此时为减函数；t＞1 时,重新组合一下试试,-4t3+t2=-t2(4t-1),t＞1 时,t2＞0,4t-1＞0都增,所以t2(4t-1) 为增函数,-t2(4t-1) 为减函数；-2t+1 也是减函数,因此t＞1 时f(t) 为减函数.也能用-4t3+t2-2t=-t(4t2-t+2),说明t＞1 时f(t)为减函数.

看到了“和积结构”联想了基本不等式：tanαtanβ(1-tanαtanβ)=tanα+tanβ,得(1-tanαtanβ)≥2,形成新方法4.

方法4 若tanα,tanβ＞0 由tanαtanβ(1-tanαtanβ)=tanα+tanβ＞0,得：0＜tanαtanβ＜1,且(1-tanαtanβ)≥2,所以2＜矛盾!

②还是通过取值代入判断可得.故而选D.

“和积结构”想到韦达定理,将tanα,tanβ看成某个方程的解.于是形成了方法5.

方法5 由tanαtanβ(1-tanαtanβ)=tanα+tanβ特征,将tanα,tanβ看着方程

的两个实数解,则有b=c(c-1).

方 程(∗∗) 的Δ=c(c3-2c2+c-4)≥0.令g(c)=c3-2c2+c-4,则g′(c)=3c2-4c+1 知,g(c)在上分别递增,在递减,极大值所以,存在唯一的2＜c0＜3 使得g(c0)=0,所以,只有c≤0,或c ≥c0时,方程(∗∗)有解.

当c＜0 时,tanα·tanβ=c＜0,故而一个角在一、三象限另一个角必在二、四象限；

当c=0 时,tanα=tanβ=0,则这两个角的终边都落在x轴上；

当c＞c0时,所以两角都在二或四象限.

综合以上分析,①错②对,选D.

我们到底要不要解方程? 其实,只要知道方程根的符号就可以解决问题,这样就可以避开高次函数单调性的讨论,于是将方法1 又简化到方法6.

方法6 当tanα＜0 时,tanβ1tanβ2=显然β可以在任何象限,②正确.

当tanα＞0 时,由知,tanα与1 的关系是解题核心!

若0＜tanα＜1,tanβ1,tanβ2＜0,则只能在第二、四象限；若tanα＞1,显然Δ=-tan2α(4 tanα-1)-(2 tanα-1)＜0,方程无解；所以①错误.

方法4 进行了估算限定,不断放缩,从而找出题目的矛盾之处,这是比较快捷的途径.沿着这个方向,我们又发现了如下的方法7 和8.

方法7 左边用二次函数最值放缩：≥tanαtanβ(1-tanαtanβ)=tanα+tanβ.

若tanα＞0,tanβ＞0,则0＜tanα,tanβ＜所以tanα+tanβ=tanαtanβ(1-tanαtanβ)＜tanα,矛盾!若tanα=0,显然tanβ=0；若tanα＜0,由方法1 可知tanβ＞0 和tanβ＜0 都有可能,如tanα=-1 代入,得：所以,正确答案为D.

方法8 右边直接去掉一个量放缩：若tanα＞0,tanβ＞0,则tanαtanβ(1-tanαtanβ)=tanα+tanβ＞tanα,且0＜1-tanαtanβ＜1；所以,tanβ(1-tanαtanβ)＞1,所以tanβ＞1.同理,tanα＞1.与1-tanαtanβ＞0矛盾! 若tanα=-1,显然tan(β+)=-tanβ,易得每个象限都有可能.所以,正确答案为D.

三角函数周期性能起到将角缩小的功能,然后再借助正切函数的单调性完成相关证明.

方法9 根据诱导公式存在mπ+α0,β=nπ+β0,(m,n ∈Z),从而有tanαtanβ=tan(α+β)⇔tanα0tanβ0=tan(α0+β0).

若tanα,tanβ＞0⇔tanα0,tanβ0＞0⇔α0,β0∈再由tan(α0+β0)=tanα0tanβ0＞0⇔α0+β0∈⇔tanα0tanβ0=tan(α0+β0)＞tanα0⇔tanβ0＞

对一道高考选择题学生择取巧的方法我们无可厚非,这是命题人的“善良”,但命题人的迎合与迁就,也使这道题失去了它最有价值的地方,教师有必要“激活”这道题的价值.

三、解题思想的延伸

解题价值最大化的有效途径是提炼出解题的关键点和解题的思想方法,在提炼的过程中可以加深对问题本质的理解,然后再在相似的问题中检验和使用,达到以一当十、以例及类的作用.

3.1 方程、函数思想的延伸

如果设x=tanα,y=tanβ本题方法1、2、3、5、6 主要是站在方程的视角,讨论方程x2y2+(1-x)y+x=0 解的符号性质,也可认为是曲线x2y2-xy+x+y=0两变量关系的寻觅,本题只是符号依存关系的寻找,是比较简单的定性关系.还可以从对称(关于直线y=x对称)、最值(用判别式法是学生比较熟悉的)、变化趋势(隐函数显化后借助导数,我们给出它的图像,如图1,其中两条切线为x=t0,y=t0)等方面去寻找.主要体现了消元和控制变量的方法,突出了函数思想的运用.

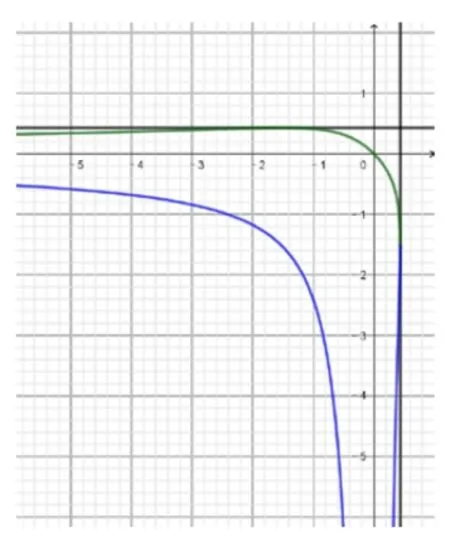
图1

借助这一思想方法,我们还可以构造新的变式：

变式1当tanα-tanβ=tan(α+β)时,α,β的依存关系如何?

解原式可化为：tanβ(tanαtanβ-tan2α-2)=0,所以,tanβ=0,或tanβ=tanα+所以,对一切当β=mπ,m ∈Z时,tanα-tanβ=tan(α-β)恒成立；当α,β满足tanβ=时,tanα-tanβ=tan(α+β) 也成立,显然tanα,tanβ符号相同.

变式2当tanα-tanβ=cot(α+β)时,α,β的依存关系如何?

变式3当1+tanαtanβ=tan(α+β)时,α,β的依存关系如何?

这两个变式读者可以自行探究,加强对方法的理解、运用甚至突破!

3.2 放缩、估算思想的延伸

方法4、7、8 以不等式为视角,体现了放缩和估算的方法,突出了反证法的功能.方法9 则以三角函数性质为视角,体现了单调性在比较大小和讨论方程根发布上的优势.所有方法都突出了先粗后细、各个击破的分类讨论思想.借助放缩、估算的思想将等与不等相互转化,我们可以解决如下比较复杂的问题.

例题在△ABC中,3(cotA+cotB+cotC)≤8 sinA·sinB·sinC,试判断△ABC的形状.

解题分析判断三角形形状通常会出现等式关系,我们估计这里要将条件中的不等式通过“两头夹”的方法创造相等关系,因此我们需要对不等式的两边分别进行估计.

不妨设A,B为锐角,令

将上式整理成关于cotA的方程：cot2A+(cotB-y)cotA+(cot2B-ycotB+1)=0,所以,Δ=(cotB-y)2-4(cot2BycotB+1)≥0,即不等式3 cot2B-2ycotB-y2+4≤0 对cotB有解,所以4y2-12(4-y2)≥0,解得当且仅当A=B=C=取等号.所以3(cotA+cotB+cotC)≥当且仅当A=B=C=取等号.

再令

当且仅当A=B时取到等号.对f(C)=(1+cosC)sinC=所以f(C)max=因此,z≤当且仅当A=B=C=取等号.所以,8 sinA·sinB·sinC≤当且仅当A=B=C=取等号.结合原题条件,得3(cotA+cotB+cotC)=8 sinA·sinB·sinC=此时满足A=B=C=.所以△ABC为等边三角形.

解题过程是一种内隐的、动态的、个性化的自主建构过程.数学教学最核心的工作就是教会学生数学思考方式.教学中教师要要把自己对问题的解读过程展现给学生,对每一个知识点的作用进行全面的联想,知识之间的连结过渡做清晰的交代；要向学生展示对问题发展的可能进行预判的技巧,通过教师的示范引领,提高思维导向作用.我们希望能自觉踏上试题的寻根之旅,剖析试题来源与发展,感悟基础的力量,理解数学知识的整体价值,培养全局观,构建联系紧密的知识网络,提高数学学习的有效性.