五局三胜制能不能用二项分布做?

华南师范大学(510631) 李晓琳

华南师范大学附中(510630) 罗碎海

在人教版普通高中课程标准实验教科书《数学》选修2-3 第59 页习题2.2 中,B 组题1 为“甲、乙两选手比赛,假设每局比赛甲胜的概率为0.6,乙胜的概率为0.4,那么采用3局2 胜制还是采用5 局3 胜制对甲更有利? 你对局制长短的设置有何认识? ”

教师教学用书中的参考答案写道：“每局比赛只有两个结果,甲获胜或乙获胜,每局比赛可以看成是相互独立的,所以甲获胜的局数是随机变量,服从二项分布.”由此引起许多数学老师对“五局三胜制能不能用二项分布做?”问题的激烈讨论.有的观点认为“赛制规则是符合高中数学新增知识‘概率与统计’中的‘二项分布’[1]”,该解法是正确的；有观点则认为是错误的,“结果一样,但从过程上看不能用二项分布,毕竟赛制决定了后面的比赛不存在”；还有观点指出,“严格来说不是二项分布,最后一局必须固定,前面几局可以用二项分布计算”.对于这个问题,本文提出了个人见解,为避免赘述,下文以“5 局3 胜”为例展开讨论.

一、两种解法

首先,关键词“5 局3 胜制”是专业术语,意为在5 局比赛中,率先取得3 局胜利的一方,获得最终胜利.以此类推,7 局4 胜、2n+1 局n+1 胜为同样的含义.接下来,我们从代数的角度来解释答案的合理性.

方法一服从二项分布,转化为事件“甲至少获胜3 局”,打满5 局.

在采用5 局3 胜制中,X～B(5,0.6),事件{X ≥3}表示“甲获胜”,所以甲获胜的概率为

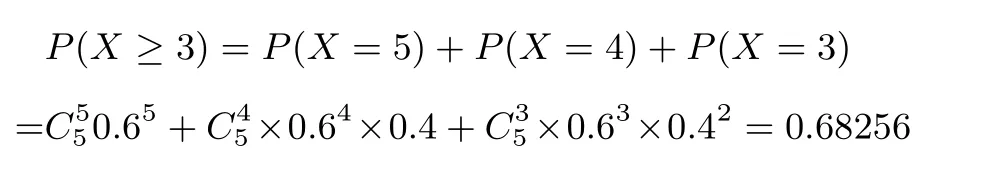
方法二确定最后一局为甲胜,前面几局按二项分布计算,甲胜则止.

按照甲乙比赛局数进行划分,固定最后一局为甲胜,比赛3 局甲获胜的概率为p1=C220.62×0.6；比赛4 局甲获胜的概率为p2=C230.62×0.4×0.6；比赛5 局甲获胜的概率为p3=C240.62×0.42×0.6.又因为每局比赛看成相互独立,则“甲获胜”的概率为

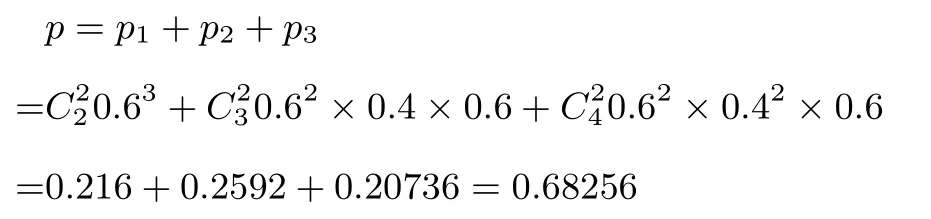
结果一样! 是巧合吗? 这决不是巧合,而是必然[2].两种解题思路不同的解法到底有什么必然的联系,我们在此继续探究.

二、解法分析

分析一按照方法一的思路,甲胜的所有比赛结果可列举如下(其中“√”表示甲胜“×”表示乙胜)：

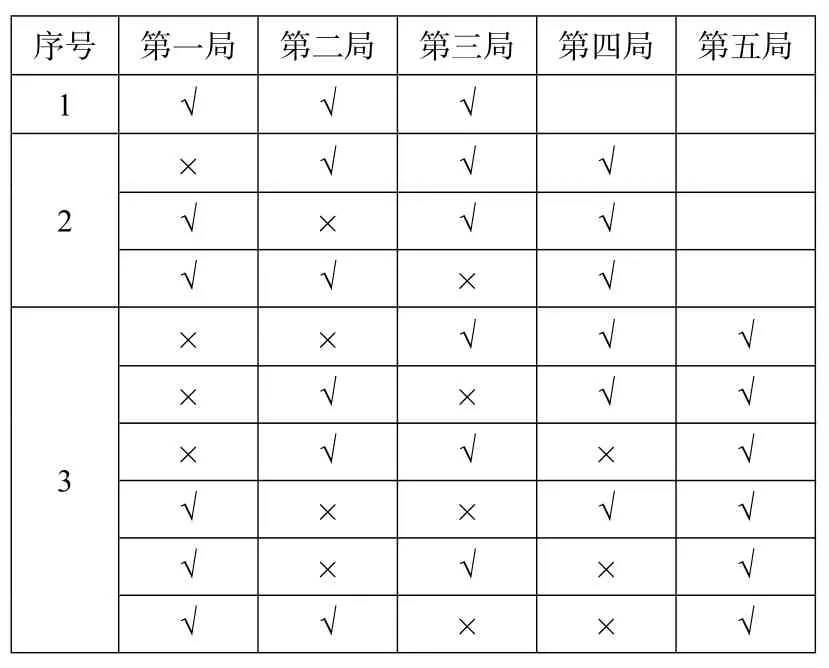
表1 “5 局3 胜”甲胜所有比赛结果

假设甲胜出后,乙队提出打友谊赛(即“为了增进友谊、交流经验、提高技术而举行的比赛”)的请求,双方协商后决定打满5 局比赛.此时,甲胜的所有比赛结果可列举如下：

表2 “打满5 局”甲胜所有比赛结果

2.4√×√√×2.5√√×√√2.6√√×√×3.1××√√√3.2×√×√√3.3×√√×√3.4√××√√3.5√×√×√3.6√√××√

这样一来打满5 局比赛,“甲战胜乙”的所有可能情况就有16 种了.

分析二根据方法二的二项式分布的计算思路,我们只需计算二项式系数之和即可.由C35+C45+C55=10+5+1=16,同样地也有16 种可能情况.

这正好说明这两种不同解法得到的结果,实则同一个事件“甲战胜乙”的概率[2].那么,两者的差异在于什么地方? (借助上表2进行说明) 按照方法一的划分,16 种可能情况被划分成3 类,每一类分别对应“1.1～1.4”、“2.1～2.6”、“3.1～3.6”；按照方法二的划分,16 种比赛结果也被划分为3 类,每一类分别对应“1.4,2.2,2.4,2.6,3.1～3.6”、“1.2,1.3,2.1,2.3,2.5”、“1.1”.因此,两者的差异在于前者以甲取胜时比赛总局数来分类,而后者以(打满比赛)甲至少能获胜的局数为分类标准.显然,“甲战胜乙”的所有可能情况的分类方式并不影响这个事件本身的概率.

三、问题深化

下面我们不妨讨论“2n+1 局n+1 胜”的情况,根据方法一和方法二的计算思路,我们分别可以得到式子：

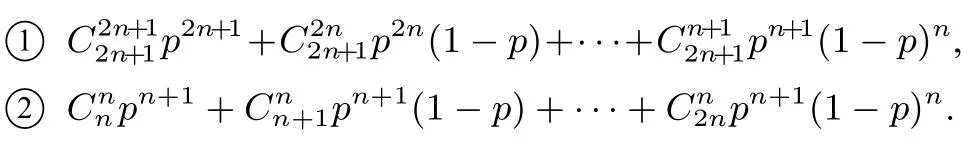
(1)赋特殊值

假设在每局比赛中甲、乙双方获胜(负) 的概率均为p=,则由组合数性质可知①=；另用数学归纳法可证易得因此,式子①、②相等.换句话说,对阵双方的运动员水平相差不大,理论上“2n+1 局n+1 胜”的赛制是公平的比赛[1].

(2)事件总数

基于上述“解法分析”提供的证明思路,“甲战胜乙”的概率不受分类方式影响,若能证明方法一和方法二的所有可能情况数相等,则说明式子①和式子②的结果是相等的.

方法一的总局数列式为

方法二(打满比赛)的总局数列式为

具体计算思路如下：

方法一由于

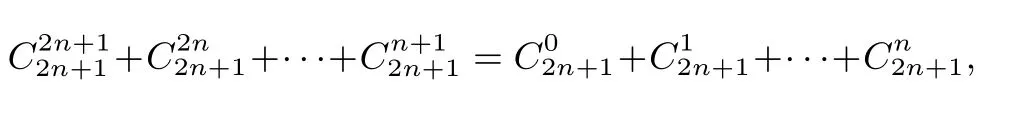
故有

方法二由已证

等式两边同乘2n,可得

因此,两种方法的计算结果均为4k(k为胜局数),从组合意义上说,式子①、②的结果相等.对于一般情形,有兴趣者不妨用代数方法加以证明!

四、总结

笔者认为,以甲队为“主元”来看,甲乙比赛问题与射击问题就有异曲同工之妙了.每局比赛甲胜的概率为0.6,乙胜的概率为0.4,而乙队获胜概率等同于甲队失败的概率；等同于一位射手击中目标的概率是0.6,其中“求甲队5 局3 胜的概率”就相当于“求射手在5 次射击中至少有3 次击中目标的概率”.

射击问题学生很容易想到用二项分布去解决问题,为什么甲乙比赛的问题就没有想到呢? 关键就在于题中出现的“5 局3 胜制”,先赢3 局就结束了,后面不再进行比赛,让人产生“打满5 局比赛的情况会与5 局3 胜产生矛盾,从而导致概率不同”的错觉,二项分布的做法不符合问题的实际背景意义.实际上,从整体的角度思考,甲获胜的局数确实服从二项分布,其计算结果也是正确的,是科学、严谨的.本文认为,当我们弄清楚背后的原理后,用二项分布“秒杀”这类题目是非常聪明的做法,是可取的!

(1) 当n=1 时,上式左边=1=右边,等式成立.

(2) 假设当n=k(k ≥1)时等式成立,即有

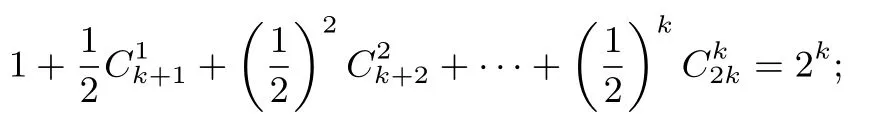
当n=k+1 时,

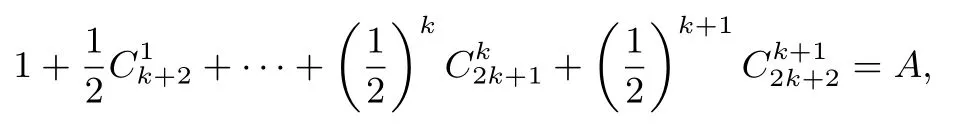
故

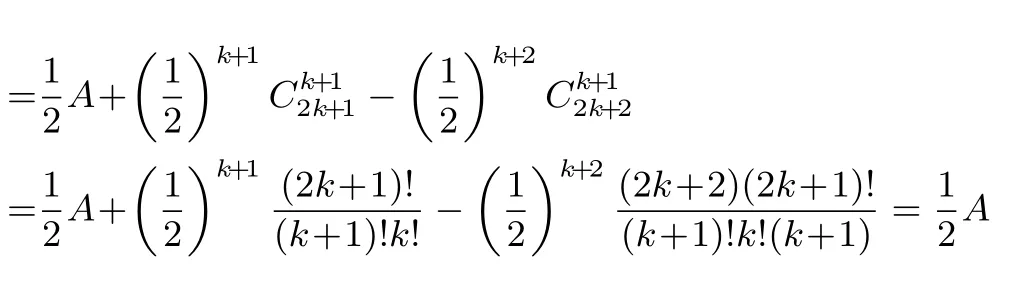
所以A=2k+1.所以当时等式也成立.由(1)(2)可知,等式对一切正整数均成立.)