基于量子衍生的图像中值滤波算法

(江苏开放大学 信息工程学院，南京 210019)

0 引言

量子力学是反映微观粒子运动规律的物理理论。不受量子系统本身的物理限制和约束，量子衍生算法借鉴量子系统规律，构造解决某些具体问题的新算法或者改进现有的算法。目前，量子衍生算法的研究内容，主要包括有：量子衍生图像处理、量子衍生神经网络、量子衍生遗传算法、量子衍生粒子群算法、量子衍生信号处理和量子衍生形态学等[1]。

2002年，美国麻省理工的Eldar Y.C.等，首次提出了量子信号处理(quantum signal processing，QSP)的概念和理论，并将量子力学的数学框架应用到信号处理领域，设计了一种量子衍生信号处理算法[2]。QSP是量子力学在信号处理领域的衍生，不依赖于量子级的物理设备，只是借鉴和利用量子力学的基本概念和数学体系等，在经典计算机上建立新的算法或对传统的经典算法进行改进。文献[3]将QSP框架应用于图像处理领域，借鉴量子力学基本理论，设计出了基于 QSP 的图像处理算法。

利用量子信息的基本原理，文献[4]定义了两种不同的像素量子比特表示形式，并针对医学图像的特点，提出了一种基于量子概率统计的图像增强算子，实验结果表明，该方法优于传统的图像增强算法。文献[5]结合量子衍生理论，提出了一种基于局部熵的量子衍生医学超声图像去斑方法，与已有方法相比，该方法能在有效去除医学超声图像斑点噪声的同时，更好地保留图像细节信息。文献[6]提出了一种基于量子衍生参数估计的医学超声图像去除斑点噪声的方法，与其它方法相比，该方法具有更好的图像细节保持能力，且去除斑点噪声效果显著。文献[7]借鉴量子叠加态建立图像像素点之间的联系，在分析一幅图像和图像的特征子图的关系基础上，提出了一种边缘检测方法。实验仿真表明，该方法的有效性和优越性。文献[8]利用量子比特表示像素点灰度，建立了一种新的边缘检测方法。该方法具有视觉补偿功能。文献[9-10]基于量子信息处理理论，将数字图像进行量子比特的表示，提出了基于量子测量和量子态坍缩的自适应中值滤波算法。与传统中值滤波器相比，算法能在保留图像细节的同时，具备更强的降噪能力，滤波效果更好。

1 量子比特和量子系统

比特(bit)是经典信息理论中的一个基本概念，通常用0和1表示。类似的，在量子信息理论[11]中，相应的一个概念是量子比特(qbit)。量子比特是量子信息理论的基础。

在量子信息理论中，一个量子比特(qbit)是一个双态量子系统，分别用基态|0>和基态|1>表示。量子比特的状态，由Hilbert空间的矢量描述，用符号|φ>表示，如下式所示：

|φ>=α|0>+β|1>

(1)

公式(1)中，α和β是基态|0>和基态|1>的概率幅，且满足|α|2+|β|2=1。|α|2和|β|2分别表示对量子比特|φ>进行测量时，获得基态|0>和基态|1>的概率。当α=0或β=0时，量子比特就坍缩为|0>或|1>。

由公式(1)可见，一个量子比特|φ>不仅仅是基态|0>和基态|1>这两种状态，而是可以是这两种状态的任意线性组合，称为量子叠加态(superposition)。一个量子比特|φ>表示的是，从基态|0>到基态|1>之间所有可能的连续状态。量子测量可以改变量子比特的状态。一旦进入量子测量，量子比特的状态将从量子叠加态坍缩到一个特定的状态。

若一个量子系统由n个量子位构成，则其中第i个量子位的状态为

|φi>=αi|0>+βi|1>

(2)

该量子系统的状态|φ>可以表示为：

|φ>=|φ1>⊗|φ2>⊗...⊗|φn>=

α1α1...α1|00...0>+α1α2...βn|00...1>+...+

(3)

ib是量子系统|φ>的第i个基态，ωi是基态ib的概率幅，概率幅满足归一化条件：

(4)

类似的，对于n个量子位的量子系统，在量子测量前，量子系统以不同概率处于2n个基态中，当进行量子测量后，量子系统的状态就会坍缩成其中一个的基态。

2 传统中值滤波算法

实际获得的图像，常会受到噪声信号的干扰。由于噪声产生的原因不同，因此，图像噪声信号的特点和噪声分布也不尽相同。常见的图像噪声信号，主要包括有：加性噪声、乘性噪声、量化噪声、盐和胡椒噪声等。图像去噪算法，通常分为空间域和频率域两种。传统的中值滤波算法，是一种空间域图像去噪算法。

传统的中值滤波算法在进行图像去噪处理时，首先是确定中值滤波窗口的大小和形状。中值滤波窗口，通常是3×3、5×5或7×7等包含奇数个像素点的方形窗口。根据待处理图像的特点和应用场合的不同，中值滤波窗口的形状，还可以选择圆形、圆环形、十字形等。实际上，中值滤波窗口的大小和形状，对中值滤波算法的滤波去噪效果影响很大。选择的中值滤波窗口越大，参与排序取中值的图像像素点也越多，相应地，算法的计算量也越大，算法运行时间也越长。

然后，将中值滤波窗口的中心像素点，与含噪声待处理图像的某个像素点重合，再对窗口覆盖区域内的所有图像像素点的灰度值，进行从小到大的排序，取排序结果的中间值，作为窗口中心位置所对应的图像像素点的灰度值。再将中值滤波窗口在待处理图像上逐个漫游一遍，依次处理其它全部的图像像素点。

一般，受噪声干扰的图像像素点的灰度值，与周围图像像素点的灰度值会有明显的差异。中值滤波算法，可以替换掉被噪声信号干扰的图像像素点的灰度值，达到图像去噪的目的。

3 量子衍生中值滤波算法

3.1 图像的量子比特表示

利用量子衍生思想设计和改进传统的图像处理算法时，首先需要将待处理图像进行归一化处理，再用量子比特的形式进行表示。

对于受噪声信号干扰的待处理图像而言，图像中的某个像素点可能是图像信号，也可能是图像信号和噪声信号的叠加。而量子比特描述了量子状态之间所有可能的连续状态，这种连续不确定的表示方式，可以描述受噪声信号干扰的图像中像素点的灰度值不确定的状态。

假设原始图像用f(m,n)表示，其中(m,n)∈Z2。对原始图像f(m,n)进行归一化处理后，结果图像为g(m,n)，则g(m,n)∈[0,1]，设g(m,n)=x，x∈[0,1]，归一化图像g(m,n)的量子比特表示为：

(5)

(6)

从概率统计的观点看，x是图像归一化处理后，像素点灰度值取值为黑点|0>的概率，1-x是像素点灰度值取值为白点|1>的概率。

传统的图像中值滤波算法，是基于中值滤波窗口的图像去噪算法。设原始图像为f(m,n)，窗口的中心像素点是fm,n，则3×3大小的方形中值滤波窗口，如式(7)所示：

(7)

量子衍生图像中值滤波算法，也是基于中值滤波窗口的去噪算法。具体来说，先对中值滤波窗口的图像像素点进行归一化处理，再对中值滤波窗口的图像像素点进行量子比特的表示。对式(7)所示的原始图像f(m,n)的3×3大小的中值滤波窗口图像，进行归一化处理。归一化处理公式，如式(8)所示：

(8)

其中:fmax和fmin是中值滤波窗口中，图像像素点的灰度最大值和灰度最小值。可见，中值滤波窗口中灰度值较小的像素点和灰度值较大的像素点，归一化处理后的灰度值分别接近0和1。

经过式(8)的归一化处理后，中值滤波窗口的图像像素点，可以表示为量子比特的形式，如式(9)所示：

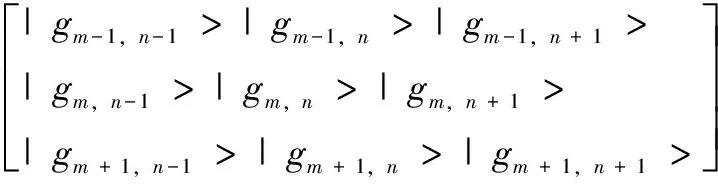
(9)

其中，

(10)

从量子信息的角度看，量子比特表示的中值滤波窗口，是一系列二值图像窗的量子叠加，当采用某种测量方式进行量子测量时，就会坍缩为一个二值图像窗。

3.2 量子Hadamard变换

根据量子信息理论，对量子比特|φ>进行量子Hadamard变换[12]，如式(11)所示：

H·|φ>=H|(α|0>+β|1>)=

(11)

根据式(11)，对黑点|0>和白点|1>的量子Hadamard变换，如式(12)所示：

(12)

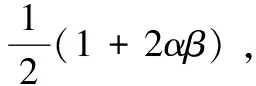
由式(12)可见，对H·|0>和H·|1>的量子Hadamard变换结果进行测量，获得|0>的概率均为0.5。

可见，与非黑、白点相比，灰度值较小的黑点和灰度值较大的白点，经过量子Hadamard变换后，获得基态|0>的概率较小。

根据式(11)和式(12)的量子Hadamard变换公式，对式(9)中用量子比特形式表示的图像中值滤波窗口中的每个像素点，进行量子Hadamard变换，如式(13)所示：

(13)

式(13)窗口中每个元素的量子Hadamard变换结果，以H·|gm,n>为例，如式(14)所示：

(14)

对式(13)中，每个像素点的Hadamard变换结果进行测量，用基态|0>的概率生成构成新的中值滤波窗口。由于图像局部区域特征不同，新中值滤波窗口的大小和形状不尽相同。

4 算法仿真与结果分析

4.1 不同强度的椒盐噪声

以MATLAB图像处理工具箱的图像pout.tif为测试图像，图像大小为291×240，椒盐噪声的强度分别为0.1、0.2、0.3和0.4。选择3×3和5×5大小的方形中值滤波窗口，比较传统中值滤波算法和量子衍生中值滤波算法的去噪效果。如图1所示，是添加了不同强度的椒盐噪声后的图像pout。

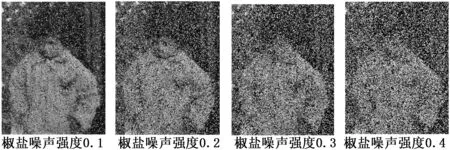
图1 不同强度椒盐噪声干扰图像

首先，选择3×3大小的方形中值滤波窗口，用传统中值滤波算法对图1受不同强度椒盐噪声干扰图像进行处理，结果图像如图2所示。

如图2所示，当椒盐噪声强度为0.3和0.4时，用3×3大小的传统中值滤波算法去噪处理后，结果图像上仍存在一些黑点和白点。

其次，采用3×3大小中值滤波窗口的量子衍生中值滤波算法，处理图1的椒盐噪声干扰图像，结果图像如图3所示。

图3 3×3量子衍生中值滤波算法结果

比较图2和图3的结果图像可见，当椒盐噪声强度为0.3和0.4时，虽然同样是3×3大小的中值滤波窗口，但从主观视觉角度观察，与图2的传统中值滤波算法图像去噪处理效果相比，图3的量子衍生中值滤波算法的去噪效果明显更好。

为比较不同大小的中值滤波窗口时，量子衍生图像中值滤波算法的去噪效果，采用5×5大小的中值滤波窗口，处理图1受不同强度椒盐噪声干扰的图像，结果图像如图4所示。

从图3和图4的结果图像可见，椒盐噪声强度为0.3和0.4时，5×5大小的量子衍生中值滤波算法明显比3×3大小的量子衍生中值滤波算法的去噪效果好。

4.2 椒盐噪声强度增加

增加椒盐噪声强度，比较3×3大小和5×5大小的中值滤波窗口时，传统中值滤波算法和量子衍生的中值滤波算法的去噪效果。

为图像pout分别添加噪声强度为0.6和0.7的椒盐噪声，如图5所示。可见，与图1中的椒盐噪声强度相比，图5中的椒盐噪声已经几乎完全覆盖原始图像pout，无法辨认清楚。

图5 椒盐噪声强度增加时干扰图像

选择3×3和5×5大小的中值滤波窗口，分别采用传统中值滤波算法和量子衍生中值滤波算法，对图5所示的椒盐噪声强度为0.6和0.7的图像进行去噪处理，算法处理结果如图6和图7所示。

图6 椒盐噪声强度0.6时算法去噪结果

从图6可见，对于椒盐噪声强度为0.6的受干扰噪声图像而言，无论是传统中值滤波算法，还是量子衍生中值滤波算法，相比3×3大小的中值滤波窗口，5×5大小的中值滤波窗口时，算法的去噪效果都更好一些。当中值滤波窗口大小一样时，量子衍生中值滤波算法的去噪效果，显然是优于传统中值滤波算法的。

如图7所示，当椒盐噪声强度为0.7时，中值滤波窗口为3×3时，传统中值滤波算法和量子衍生中值滤波算法，去噪效果均较差。中值滤波窗口为5×5时，两种算法的去噪效果有明显改善。此时，相比传统中值滤波算法，量子衍生中值滤波算法的去噪效果最好。

图7 椒盐噪声强度0.7时算法去噪结果

4.3 客观评价指标

针对受不同强度椒盐噪声干扰的图像，对于传统中值滤波算法和量子衍生中值滤波算法的算法去噪效果比较，除了主观视觉评价外，还可以采用信噪比SNR、边缘保持度β等客观评价指标来评价衡量算法去噪效果。

客观评价指标信噪比SNR，反映的是算法处理后的结果图像和原始图像之间的像素灰度值的差异。信噪比SNR的计算公式，如下所示：

(15)

假设f1(x,y)表示原始图像，f2(x,y)表示算法处理后的结果图像。根据式(15)的计算公式可以看出，如果SNR的值越大，则表示原始图像和算法去噪处理后的结果图像的差异越小，说明算法的去噪效果好。

比较图6和图7中，椒盐噪声强度为0.6和0.7时，采用不同大小中值滤波窗口时，传统中值滤波算法和量子衍生中值滤波算法处理后，图像信噪比SNR的计算结果，如表1所示。

由表1可以看出，表1中的信噪比SNR数值，与从主观视觉角度观察图6和图7的算法处理结果是一致的。从主观视觉角度看，图6和图7中，都是中值滤波窗口为5×5

表1 不同算法的信噪比SNR值

时，量子衍生中值滤波算法效果最佳。相应地，该算法在表1中对应的SNR计算值也是最大，分别为15.282和12.914，也说明算法去噪效果最佳。

如图7所示，当椒盐噪声强度为0.7，中值滤波窗口为3×3时，传统中值滤波算法和量子衍生中值滤波算法的效果都较差。相应地，根据表1中的信噪比SNR数据，算法对应的信噪比SNR值分别为3.376 6和2.033 4。可以看出，信噪比SNR值也较小，这说明结果图像与原始图像之间的像素灰度值差异较大，算法的去噪处理效果不佳。

如图7所示，当中值滤波窗口为5×5时，传统中值滤波算法和量子衍生中值滤波算法的效果有所改善。根据表1中的信噪比SNR数据，两种算法处理后，SNR的计算值分别为7.658 3和12.914，SNR值有明显增加，表明结果图像与原始图像之间差异较小，算法去噪处理效果好。其中，5×5大小的量子衍生中值滤波算法去噪效果最好，信噪比SNR的值也最大。

对于椒盐噪声为强度为0.6的噪声干扰图像而言，3×3大小中值滤波窗口的量子衍生中值滤波算法的效果，不如5×5大小的量子衍生中值滤波算法，这点从图6的结果图像和表1的结果图像SNR值都可以看出。

客观评价指标边缘保持度β，表示的是算法去噪处理后的结果图像与原始图像之间的边缘差异，用来衡量算法对图像边缘信息的保持能力。边缘保持度β的计算公式如下：

f1是原始图像，Δf1是原始图像f1经过拉普拉斯高通滤波算子滤波处理后的图像。f2是某算法对原始图像f1处理后的结果图像，Δf2是结果图像f2经过拉普拉斯高通滤波算子滤波处理后的图像。

边缘保持度β的取值范围在0～1之间，β的取值越大，表明结果图像边缘信息保持的越好。当β=1时，说明结果图像f2和原始图像f1完全一样。

利用公式(16)的边缘保持度β的公式，计算图6和图7中结果图像的边缘保持度β，结果如表2所示。计算时采用的拉普拉斯高通滤波算子系数为(-1,0,-1;-1,4,-1;0,-1,0)。

从表2的不同算法结果图像的边缘保持度β数据可以看出，椒盐噪声强度为0.6时，5×5的量子衍生中值滤波算法处理后，结果图像的边缘保持度最佳，3×3中值滤波算法最差。对应表1的SNR数据，3×3中值滤波算法处理后，结果图像的信噪比值SNR也是最小。

表2 不同算法结果图像的边缘保持度

椒盐噪声强度为0.7时，3×3量子衍生中值滤波算法处理后的结果图像的边缘保持度最差，5×5量子衍生中值滤波算法处理后的结果图像的边缘保持度最佳，这与图7的主观视觉角度的观察结论一致。

5 结束语

本文提出了一种基于量子衍生的图像中值滤波算法，针对不同程度的椒盐噪声，先后采用不同大小的中值滤波窗口，与传统中值滤波算法相比较，对受椒盐噪声信号干扰的图像进行算法去噪仿真，并对算法处理后的结果图像，进行了主客观评价。算法仿真结果表明，较之传统中值滤波算法，当分别选择3×3和5×5大小的中值滤波窗口时，5×5大小的量子衍生中值滤波算法是一种更为有效的去噪算法。