杨氏双缝干涉实验的条纹分布研究

李栋玉，时有明，张廷宪

杨氏双缝干涉实验的条纹分布研究

李栋玉，时有明，张廷宪

（曲靖师范学院 物理与电子工程学院，云南 曲靖 655011）

为了研究杨氏双缝干涉实验条纹的分布情况，通过理论推导结合Origin软件仿真得出干涉条纹的分布图像，计算出不同区间内条纹的宽度。对干涉条纹宽度变化规律的曲线拟合分析显示，条纹的宽度随偏离图样中心距离的增加呈现指数增长，这一增长趋势在远场区域非常明显。对比教材中使用二次近似处理计算近场区域条纹宽度的结果，发现当-0.01 m≤≤0.01 m时，仿真结果与近似处理的计算结果一致。

双缝干涉；干涉条纹；仿真实验；光学实验

牛顿在1704年出版了《光学》著作，书中认为光是由一群具有一定速度的粒子组成，这演变为后来光的粒子学说；而惠更斯早在1690年在《光论》一书中提出了光的波动学说。1801年托马斯·杨（Thomas Young）完成了著名的双缝干涉实验，证明光具有波动性，并在1807年出版的《自然哲学与机械学讲义》一书中详细描述了双缝干涉实验[1]。杨氏双缝干涉实验为光的波动理论发展奠定了坚实的基础，此后，爱因斯坦和德布罗意等人提出光的波粒二象性理论，对物理学发展产生了巨大的推动作用。2002年9月美国出版的《物理世界》杂志将杨氏双缝干涉实验评选为物理学史上最美的10个经典实验之一[2]。目前在有关波动光学的教材中主要采用“近似”的方法分析该实验，得出的干涉条纹是等间距、均分布的典型特征[3-5]。“近似”的分析只局限于近场区域（观测点离图样中心较近）的条纹分布，对远场区域（观测点离图样中心较远）条纹的分布完全不适用。本文采用非近似理论推导和Origin软件仿真，对杨氏双缝实验近场和远场的条纹线度分布特征进行了定量研究。

1 理论推导

杨氏双缝干涉实验模型如图1所示。

光源S发出的光波波面传播到双缝S1和S2上，形成2列相干光源。单缝S处于双缝S1和S2的对称位置，光程SS1和光程SS2相等，不引入光程差。因此光源S1和S2具有相同的初相位0和圆频率，其振动方程可表示为：

图1 杨氏双缝干涉实验模型

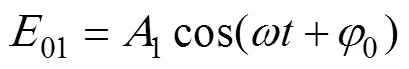
S1和S2作为波源分别产生一列波动传播到场点，并各自在点引起一个振动，点的两个振动相对于波源S1和S2均有延迟，延迟的时间由S1和S2到点的距离1、2和波速1、2决定。点的两个振动表达式为：

式中1和2是两列光波的传播速度，本实验中两列光波在空气中传播，因此1和2相等，均等于。根据旋转矢量叠加方法，可得点的光强为

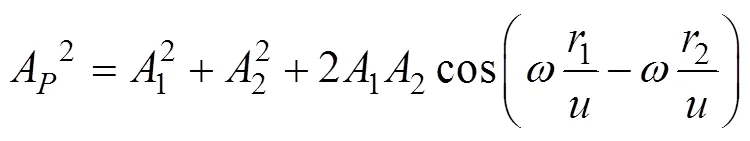
而

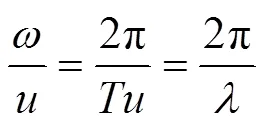
其中：为周期，为光在空气中的波长。

将式（6）代入式（5）得：

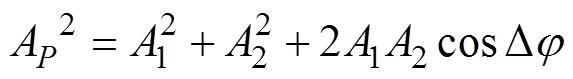
其中

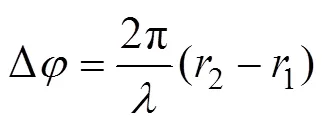
从式（7）可知：场点叠加后的振幅P的取值取决于2-1。其实2-1即为两束光的光程差。设双缝之间的距离S1S2＝，双缝到光屏的距离为，点的坐标为。实验中，一般是mm量级，是m量级。在近场条件下，从图1中可得

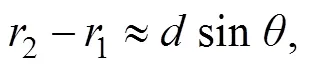
而

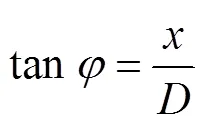
由式（9）、式（10）和式（11）得

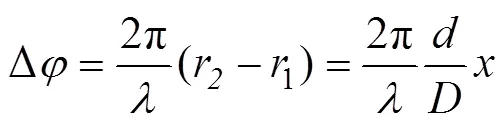
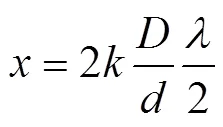
由式（14）可得出条纹间距与点的位置无关的结论，即条纹呈现均匀分布[3]。目前的波动光学教材均分析到此为止，未对远场情况下条纹的分布情况加以讨论。上面的分析过程，采用了两次近似处理，仅适用于近场条件。在波动光学的教材中，对何为近场、何时可以取近似计算未进行详细的探讨，导致学生在学习该知识点时没有一个确切的依据，使得客观的知识融入了一定的主观性。

以下为通过几何关系严谨地推导2-1的取值。根据图1的几何关系可得：

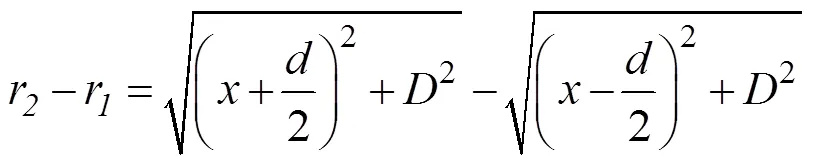
将式（15）代入式（7），可以得出任意情况下（包含近场区域、远场区域）的光强分布函数[6-8]为

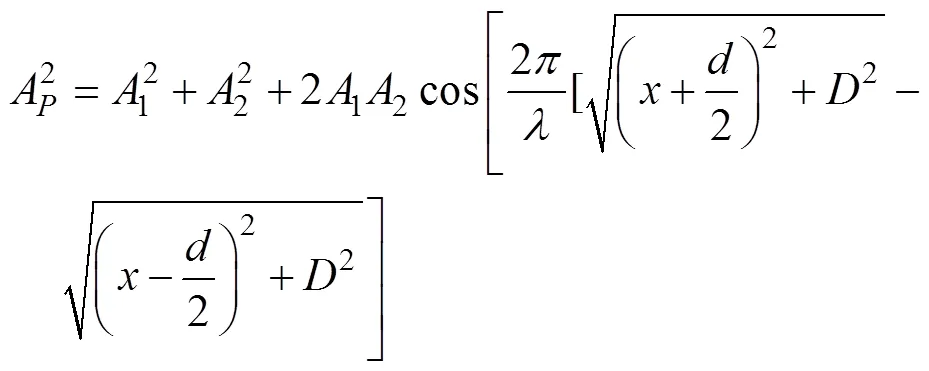
2 干涉条纹仿真

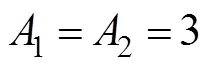
调整显示区间便可观察到杨氏双缝干涉实验的条纹分布。在光屏xoy平面内，-0.005 m≤x≤0.005 m和-0.005 m≤y≤0.005 m区间范围内的干涉条纹如图2所示。

表1 0~0.15 m范围内的拟合参数及标准误差

图3 0~0.15 m范围条纹宽度变化规律的曲线拟合

从图3可看出：杨氏双缝干涉条纹宽度在光场中的分布是非均匀的，在轴上随着远离中心对称位置，条纹的宽度呈现指数增长。明条纹的中心坐标由光程差与波长之间的整数倍决定，可表示为：

从式（17）可以看出，由于干涉级数只能取整数，的取值将不再连续。在近场条件下，教材的处理方法采用两次近似得到式（14）用于计算条纹的宽度。现将模拟参数和代入式（14），计算得出近场条件下条纹的宽度为0.0011 m。

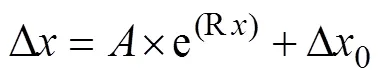
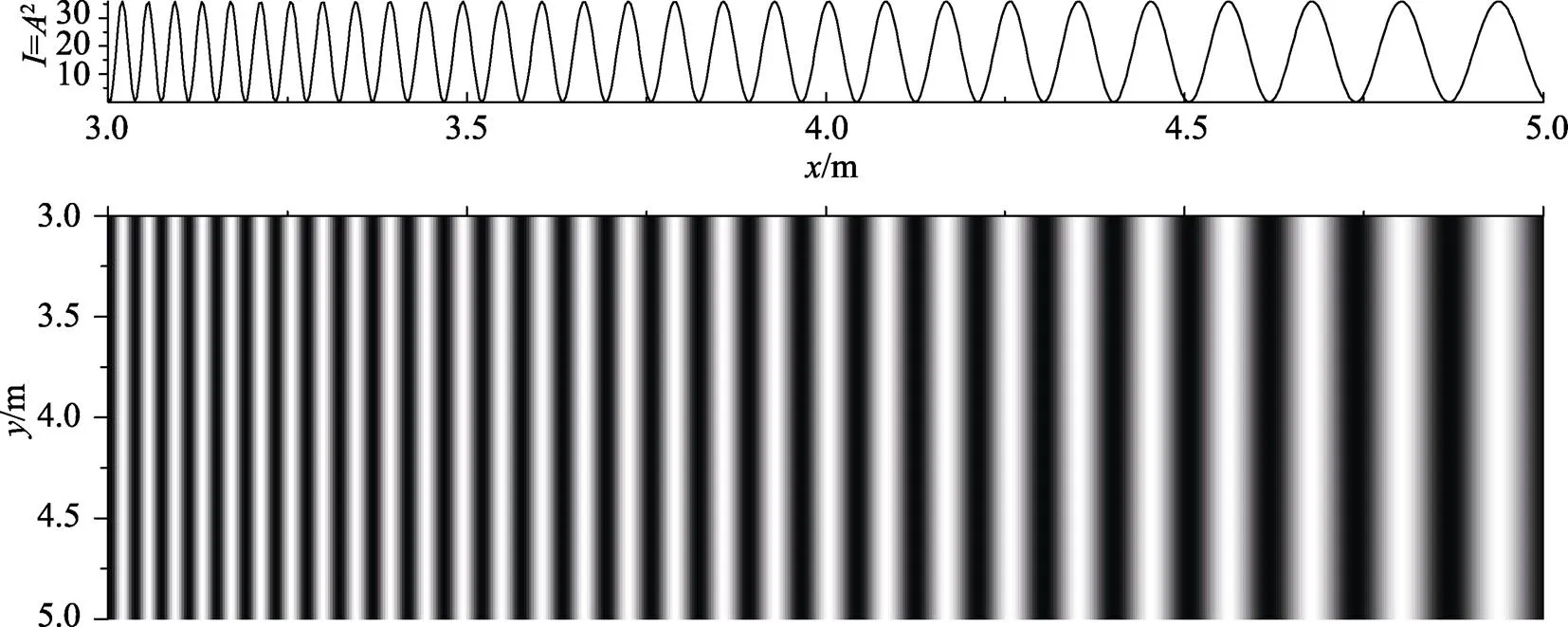
图4 3 m≤x≤5 m、3 m≤y≤5 m区间范围内干涉条纹分布情况

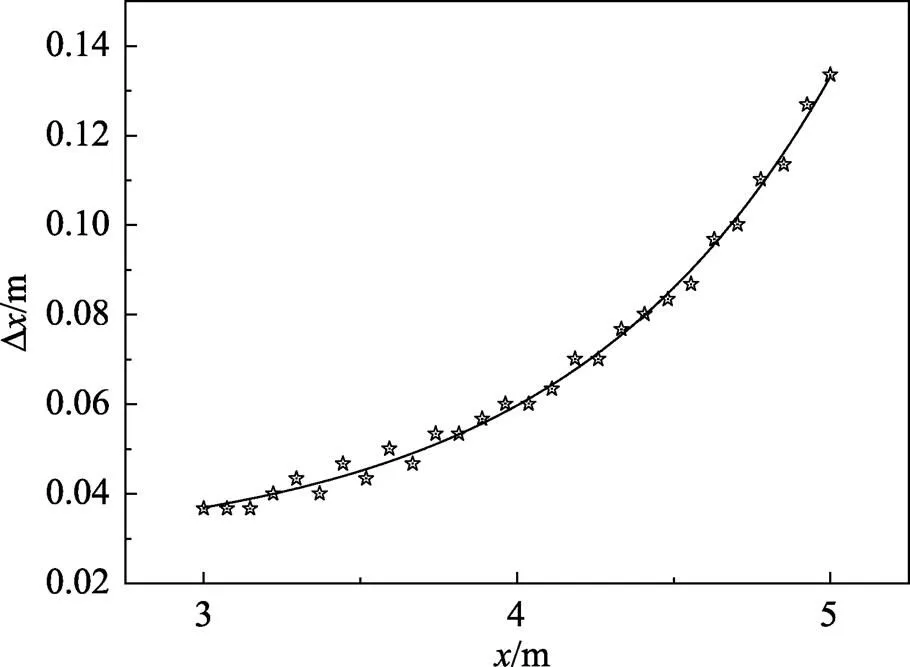
图5 3~5 m范围条纹宽度变化规律的曲线拟合

表2 3~5 m范围拟合参数及标准误差

3 结论

通过理论推导得出的非近似处理的光强分布函数，以及用Origin 9.0仿真得到的光强分布图像表明，曲线拟合显示条纹的宽度随远离中心对称位置呈指数函数的形式增加。在＝0.5 mm、＝1 m、＝550 mm 的参数条件下，–0.01 m≤≤0.01 m范围内仿真的条纹宽度结果与两次“近似”计算得出的结果一致，该范围可称为近场区域。

[1] 孙敬姝，李志有，梁浩.托马斯杨的干涉实验：“最美丽”的十大物理实验之六[J].物理通报，2003(9): 37–38.

[2] 徐力遥.史上最美的物理实验：杨氏双缝干涉实验[J].物理之友，2015, 31(6): 48.

[3] 姚启钧.光学教程[M].北京：高等教育出版社，2014.

[4] 程守洙.普通物理[M].北京：高等教育出版社，2005.

[5] 张宇，赵远.大学物理[M].北京：机械工业出版社，2011.

[6] 何坤娜，韩萍，朱世秋，等.杨氏双缝干涉图样的理论模拟[J].物理通报，2016(3): 25–28.

[7] 谭毅.杨氏双缝干涉实验的仿真研究[J].实验技术与管理，2012, 29(3): 91–93, 190.

[8] 何坤娜，黄坚.杨氏双缝干涉条纹的空间分布及理论模拟[J].物理与工程，2016, 26(5): 12–15.

[9] 曹卫军，赖康荣.基于Origin的波动光学实验仿真[J].大学物理，2015, 34(1): 49–52, 65.

[10] 唐小村.基于Origin的光栅衍射仿真实验[J].大学物理实验，2018, 31(6): 101–103.

[11] 邢静. Origin软件在大学物理实验中的应用[J].信息技术与信息化，2018(4): 133–135, 141.

[12] 谢英英，罗晓琴，唐金龙，等. Origin9.1在液体表面张力系数测定的数据处理中的应用[J].大学物理实验，2017, 30(3): 118–120.

Study on fringe distribution of Young’s double slit interference experiment

LI Dongyu, SHI Youming, ZHANG Tingxian

(College of Physics and Electronic Engineering, Qujing Normal University, Qujing 655011, China)

double slit interference; interference fringes; simulation experiment; optical experiment

O436.1

A

1002-4956(2019)10-0120-03

10.16791/j.cnki.sjg.2019.10.028

2019-03-27

国家自然科学基金项目（31760341）资助；云南省教育厅科研项目（2015Y425）资助

李栋玉（1983—），女，四川绵阳，硕士，讲师，主要研究方向为光谱信息挖掘。E-mail: ldy8304@163.com