从一道中考题的解法争议谈起

山东省聊城第六中学 (邮编：252000)

1 问题呈现

2016年贵州省黔南州的一道中考题：

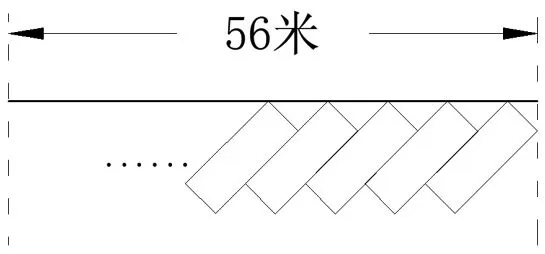
图1

在一次区域教研活动中，上述中考题的解法引发许多教师的争议.但是，尽管议论颇多，可还是最终未果.那么争议中主要观点是什么，又怎样才能消除争议呢？对此，笔者做些梳理和分析，并以此与同仁交流.

2 争议情况

2.1 无争议部分

图2

因此，根据题意知：

2.2 争议中的主要观点

3 解法探究

上述中考题与一般的近似计算题不同，它的独特之处在于，要通过一个近似取值范围求停车位的精确值，而不是求其近似值，但由于计算误差的原因，难以确定该近似范围中是否包含所求的精确值.因此，有必要对上述近似范围进行必要的修正，使其包含所求的精确值.然而，从观点1到观点3，都把停车位数x的近似取值范围视为精确范围来对待，因而均未考虑误差的影响，并由x的近似范围直接得出所谓的精确值，这就混淆了近似范围与精确范围的不同本质，故都是不严谨的.

那么，如何通过考察误差来修正上述近似范围，进而找到精确值呢？

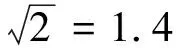
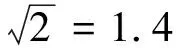
4 反思辨析

以上所探究的虽然是一道具体的近似计算问题，但回溯从观点1到观点3的不同见解，其背后却折射出它们对近似计算问题的解读都存在一定偏颇，值得警惕与反思.

图3

这里需要明晰一个问题：如果一定要要提高所用近似数据的精确度，那么将其提到什么精度，才能使由此得到的近似范围中包含所求的精确值？

从上述分析来看，因为近似计算结果的精确度并非只受所用近似数据精确度的影响，还有其他因素的影响，所以这个问题必须通过对最终近似结果进行综合性的误差分析方可确定.因此，即使要提高所用近似数据的精确度，误差分析仍在“幕后”起着关键作用.

5 写在后面

诚然，根据观点1、观点2和观点3能够处理某些较简单的近似计算问题，但也应看到它们都有一定的局限性，比如：它们都未充分考虑误差传播问题的复杂性，进而均未认识到“误差分析”也是解答近似计算问题的一个关键环节.因此，在近似计算问题中，应特别重视误差的传播对计算结果的影响，在希望计算方法简便而有效的同时，还应认真研究问题的特殊性及相应算法模式的内在结构特征，并针对各种因素可能引发的误差进行误差分析，以有效控制误差的传播与积累，从而保证在有计算误差影响的情况下仍能得到所需的可靠结论.