利用试题资源 进行探究教学

江苏省太湖高级中学 (邮编：214125 )

数列是高中数学的重要内容之一，在高考中占重要地位．2017年江苏卷的19题是数列，其编拟独特，手法巧妙，体现江苏试题“在朴实中重基础，在常规中考能力，在平和中透灵气”的命题特色，充分体现高考试题的教学导向性．高考试题是教学的重要资源，笔者利用此题进行探究教学，得到一般性的结论，进而类比到等比数列，现将探究历程撰写成文与大家交流．

1 试题呈现

对于给定的正整数k，若数列{an}满足：an-k+an-k+1+…+an-1+an+1+…+an+k-1+an+k=2kan对任意正整数n(n>k)总成立，则称数列{an}是“P(k)数列”．

(1)证明：等差数列{an}是“P(3)数列”；

(2)若数列{an}既是“P(2)数列”，又是“P(3)数列”，证明：{an}是等差数列．

答案(1)因为{an}是等差数列，设其公差为d，则an=a1+(n-1)d，从而，当n≥4时，an-k+an+k=a1+(n-k-1)d+a1+(n+k-1)d=2a1+2(n-1)d=2an，k=1,2,3，所以an-3+an-2+an-1+an+1+an+2+an+3=6an，因此等差数列{an}是“P(3)数列”．

(2)数列{an}既是“P(2)数列”，又是“P(3)数列”，因此，当n≥3时，an-2+an-1+an+1+an+2=4an①，当n≥4时，an-3+an-2+an-1+an+1+an+2+an+3=6an②． 由①知，an-3+an-2=4an-1-(an+an+1)③，an+2+an+3=4an+1-(an-1+an)④，将③④代入②，得an-1+an+1=2an，其中n≥4，所以a3,a4,a5,…是等差数列，设其公差为d′．在①中，取n=4，则a2+a3+a5+a6=4a4，所以a2=a3-d′，在①中，取n=3，则a1+a2+a4+a5=4a3，所以a1=a3-2d′，所以数列{an}是等差数列．

2 探究历程

2．1 不识庐山真面目，只缘身在此山中

师：本题注重基础，起点低，落点高，突出对等差数列概念及通项公式的考查．由此想到苏教版高中数学教材必修5第36页例3：

可见，19题是源于此题．谁能用“P(k)数列”的定义来表述例3吗？

生：(1)等差数列{an}是否为“P(1)数列”？(2)若数列{an}是“P(1)数列”，那么数列{an}一定是等差数列吗？

师：从上述两题可知，等差数列{an}是“P(1)数列”，也是“P(3)数列”，由此你能得到什么结论？

生：对于任意的正整数m(n>m)，等差数列{an}都是“P(m)数列”．

师：谁能给出证明？

生：因为{an}是等差数列，设公差为d，则an=a1+(n-1)d，从而，当n≥m+1时，an-k+an+k=a1+(n-k-1)d+a1+(n+k-1)d=2a1+2(n-1)d=2an，k=1,2,3,…,m，所以an-m+an-m+1+…+an-2+an-1+an+1+an+2+…+an+m-1+an+m=2man，因此等差数列{an}是“P(m)数列”．

2．2 山重水复疑无路，柳暗花明又一村

师：由例3知：若数列{an}是“P(1)数列”，则数列{an}是等差数列．请问：如果数列{an}是“P(2)数列”，那么数列{an}一定是等差数列吗？

生：若数列{an}是“P(2)数列”，则an-2+an-1+an+1+an+2=4an，无法消掉其中的an-2和an+2得到an-1+an+1=2an，所以无法证明数列{an}是等差数列．

师：同样，若数列{an}是“P(3)数列”，也无法证明数列{an}是等差数列．由此你能得到什么结论？

生：若数列{an}是“P(m)数列”(m∈N*,m≥2)，都不能得到数列{an}是等差数列．

师：要证明数列{an}是等差数列，难道仅要满足第(2)题中的条件吗？

生：有！如：若数列{an}既是“P(2)数列”，又是“P(4)数列”，则数列{an}是等差数列．

师：证明试试．

生：由数列{an}是“P(2)数列”，当n≥3时，得an-2+an-1+an+1+an+2=4an①．由数列{an}是“P(4)数列”，当n≥5时，得an-4+an-3+an-2+an-1+an+1+an+2+an+3+an+4=8an②．分别以n-2和n+2代换①中的n，得an-4+an-3=4an-2-(an-1+an)③，an+3+an+4=4an+2-(an+an+1)④，将③④代入②，得an-2+an+2=2an，其中n≥5，无法确定数列{an}是等差数列．

师：由an-2+an+2=2an(n≥5)你能得到什么？

生：可得数列a3,a4,a5,…的2个子数列a3,a5,a7,…、a4,a6,a8,…都是等差数列．

师：可见上述猜想也是有价值的！还能想到什么？

生：若数列{an}既是“P(2)数列”，又是“P(5)数列”，则也能得数列{an}子数列为等差数列！

师：证明试试．

生：同理可得an-3+an+3=2an，其中n≥6，可得数列a3,a4,a5,…中的3个子数列a3,a6,a9,…，a4,a7,a10,…，a5,a8,a11,…都是等差数列．

师：很好！还能想到什么？

生：若数列{an}既是“P(2)数列”，又是“P(6)数列”，也能得到数列{an}子数列是等差数列！

师：再证试试．

生：可得5(an-4+an+4)+(an-1+an+1)=12an，无法得到数列{an}的子数列是等差数列．

师：虽然失败，但是上述尝试也是有价值的，由此你能得到什么结论？

生：若数列{an}既是“P(2)数列”，又是“P(m)数列”(m≥6,m∈N*)，无法确定数列{an}的子数列是等差数列．

师：由此可见，试题第(2)题的命制是非常巧妙的，真是“试题本天成，妙手偶得之”，给人留下清新飘逸的感觉！那么，在“P(k)数列”定义下，要证明数列{an}是等差数列，难道真的没有其他条件吗？

生：因为数列a3,a4,a5,…的2个子数列a3,a5,a7,…，a4,a6,a8,…是等差数列；它的3个子数列a3,a6,a9,…，a4,a7,a10,…，a1也是等差数列．若上述条件同时成立，则数列{an}是等差数列．

师：很好！若数列{an}既是“P(2)数列”，又是“P(4)数列”和“P(5)数列”，则数列{an}是等差数列．谁能给出证明？

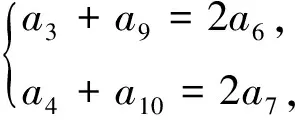
2．3 千淘万漉虽辛苦，吹尽狂沙始到金

师：漂亮！由此还能想到什么？

生：若数列{an}既是“P(3)数列”，又是“P(6)数列”和“P(7)数列”，则数列{an}是等差数列．

师：谁来证明？

生：同上，若数列{an}既是“P(3)数列”，又是“P(6)数列”，可得an-3+an+3=2an，其中n≥7，所以数列a4,a5,a6,…的3个子数列a4,a7,a10,…，a5,a8,a11,…，a6,a9,a12,…都是等差数列．

当数列{an}既是“P(3)数列”，又是“P(7)数列”时，得an-4+an+4=2an，其中n≥8，所以数列a4,a5,a6,…的4个子数列a4,a8,a12,…，a5,a9,a13,…，a6,a10,a14,…，a7,a11,a15,…都是等差数列．

不妨设数列a4,a5,a6,…的3个子数列a4,a7,a10,…、a5,a8,a11,…，a6,a9,a12,…的公差分别为d1，d2，d3．

又因为数列a4,a5,a6,…的4个子数列a4,a8,a12,…，a5,a9,a13,…，a6,a10,a14,…、a7,a11,a15,…都是等差数列．所以

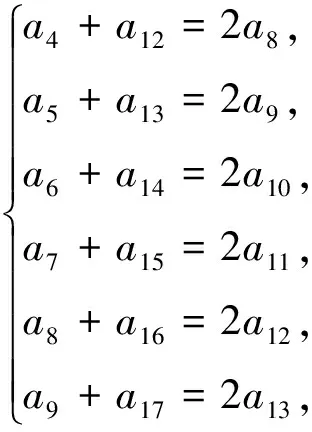
由(4)-(1)得d1+d3=2d2，由(5)-(2)得d1+d2=2d3，由(6)-(3)得d2+d3=2d1，解得d1=d2=d3，代入(1)得a4+a6=2a5，所以a4,a5,a6三项是等差数列，记公差为d．

在an-3+an-2+an-1+an+1+an+2+an+3=6an中，取n=7时，则a4+a5+a6+a8+a9+a10=6a7，即6a4+6d+4d1=6a4+6d1，解得d1=3d，所以数列a4,a5,a6,…是以d为公差的等差数列．

在an-3+an-2+an-1+an+1+an+2+an+3=6an中，依次取n=6,5,4，可得a3=a4-d，a2=a4-2d，a1=a4-3d，所以数列{an}是以a1为首项，d为公差的等差数列．

师：真棒，我们该为他鼓掌！上述结论虽然没有原题简洁，但是很有价值！由此你能想到什么呢？

生：若数列{an}既是“P(m)数列”，又是“P(2m)数列”和“P(2m+1)数列”(m≥2,m∈N*)，则数列{an}是等差数列．

师：很好！由特殊到一般，这个猜想正确吗？

生：同上，由数列{an}既是“P(m)数列”，又是“P(2m)数列”可得an-m+an+m=2an，其中n≥2m+1，所以数列am+1,am+2,am+3,…的m个子数列am+1,a2m+1,a3m+1,…；am+2,a2m+2,a3m+2,…；am+3,a2m+3,a3m+3,…；…；a2m,a3m,a4m,…都是等差数列．

同样由数列{an}既是“P(m)数列”，又是 “P(2m+1)数列”可得，数列am+1,am+2,am+3,…的m+1个子数列am+1,a2m+2,a3m+3,…，am+2,a2m+3,a3m+4,…，…，a2m+1,a3m+2,a4m+3,…都是等差数列．

不妨设数列am+1,am+2,am+3,…的m个子数列am+1,a2m+1,a3m+1,…，am+2,a2m+2,a3m+2,…，…，a2m,a3m,a4m,…的公差分别为d1，d2，…，dm，则有

师：在“P(k)数列”定义下，我们得到一个数列是等差数列应满足的一般条件，由此你还能想到什么？

生：可类比到等比数列：对于给定的正整数k，若各项均大于0的数列{an}满足：

an-kan-k+1…an-1an+1…an+k-1an+k=an2k对任意正整数n(n>k)总成立，则称数列{an}是“Q(k)数列”.

(Ⅰ)对于任意的正整数m(n>m)，等比数列{an}是“Q(m)数列”；

(Ⅱ)若数列{an}既是“Q(2)数列”，又是“Q(3)数列”， 则数列{an}是等比数列；

(Ⅲ)若数列{an}既是“Q(m)数列”，又是“Q(2m)数列”和 “Q(2m+1)数列”m≥2,m∈N*， 则数列{an}是等比数列[2]．

师：很好！对于上述结论，请大家课后给予证明，谁来总结一下我们本节课所学的内容？

生：……

师：下课！

3 课后感想

本节课是对一道高考试题的溯源和探究，培养学生不怕失败、勇于实践、勤于探索的科学精神，加深了学生对问题本质的认识，促进了学生思维能力的发展，提高了学生分析问题和解决问题的能力，提升了学生的数学核心素养，同时深深感觉到高三数学复习必须做好如下两点：

(1)高三复习要用好教材

在历年全国各地的高考试题中都有一部分试题是由教材的例题、习题改编而来的，这要求一线教师必须重视教材例题、习题教学，不能舍本逐末，脱离教材，利用一本资料打天下，而是要回归教材，备课组要加强对教材典型例题、习题的教学研究，每次集体备课之前布置要研讨的例题、习题，要求备课组全体成员都要提供一到两个改编方案，发挥集体的智慧，提高改编试题的质量，并将改编质量高的试题运用到平时的测试中，以引起学生重视对课本例题、习题的学习，充分发挥它们的教学价值．

(2)高三复习要用好考题

各地的高考试题都是专家组经过多次打磨而成，质量非常高，能较好地对考生知识与能力进行考查，在实际教学中部分教师错误地认为这些试题已经是昨日黄花，绝对不会在高考试题中再次出现，没有再研究的必要．事实上，通过对高考试题的研究，不但可以找到问题的源头，理清问题间的关系，将特殊问题探究推广到一般情形，再进行变式拓展，挖掘其中蕴藏规律，揭示问题的本质，形成知识体系．通过研究也可以明确命题者的意图，发挥高考试题的导向功能，为高三数学复习指明方向．