基于物理设计约束的模拟电路尺寸设计的优化算法GMSGA

梁生欣，王梦硕，杨 帆，严昌浩，曾 璇，周 电

(复旦大学 专用集成电路与系统国家重点实验室，上海 201203)

相较于数字电路，模拟电路的晶体管尺寸的确定(analog circuit sizing[1])过程计算复杂，且电路指标受工艺影响较大.近些年来，模拟电路尺寸设计取得了长足的发展.为解决模拟电路尺寸设计的自动化问题，人们提出两种基本方法： 基于知识(knowledge-based)的方法和基于优化(optimization-based)的方法[1].基于知识的方法需要人工地建立电路库，缺乏普适性和灵活性.如图1所示，基于优化的方法将电路尺寸设计问题看作数学优化问题，电路性能指标作为优化目标或优化约束，电路尺寸作为优化变量.在基于优化的方法中，基于公式(equation-based)的方法通过手工推导的公式或者数学建模的方法评估电路的性能指标，计算精度不高但优化速度快；而基于仿真(simulation-based)的方法通过仿真工具SPICE(Simulation Drogram with Integrated Circuit Emphasis)评估电路的性能指标，优化速度慢但计算精度高.由于具有更高的计算精度，基于仿真的方法成为模拟电路自动化尺寸设计的主流方法，但减少仿真次数成为亟待解决的重要问题.一些数值优化算法，诸如： 梯度下降法、模拟退火法[2]、几何规划法[3]、遗传算法[4]等，可以加快收敛速度，减少仿真次数.

图1 基于优化的电路尺寸设计方法[1]Fig.1 Optimization-based sizing approach[1]

但是，模拟电路尺寸的自动化设计需要考虑物理设计.例如，MOS(Metal-Oxide-Semiconductor，金属-氧化物-半导体)晶体管的多叉指(multi-finger)结构是版图设计中的常见结构，叉指数是离散型的整数变量.但是多数的自动化工具将叉指数等和物理设计相关的变量看作连续变量求解，最后上下取整.然而对于灵敏度高的变量这样做会极大地改变性能参数的优化结果.因此，在电路前仿真设计阶段考虑物理设计所引入的整数变量是必要的.在传统的解决混合整数规划问题的方法之中，松弛法是常见的方式之一，然而物理设计中的部分整数变量如叉指数无法设定为非整数，故在该问题中难以适用.其他的传统方法诸如分支定界法等方法在高维离散变量空间或大量离散决策空间下耗时巨大，不适用于基于仿真的方法.差分进化算法[5](Differential Evolution, DE)是一种新兴的算法，以其实现简单和收敛快速从而实际应用广泛，通过对输入上下取整，DE依然能快速地收敛得到良好的离散问题的结果，可以作为该类问题的解决方法之一.但是DE作为启发式算法有一些超参数需要人工设定，对于不同的问题其算法鲁棒性不佳，算法稳定性不好.

本文在基于仿真的自动化设计方法的框架下，提出一种考虑版图物理设计的模拟电路尺寸设计算法： 混合高斯采样贪婪算法(Gaussian Mixture Sampling Greedy Algorithm, GMSGA).该算法将尺寸设计问题看作非线性混合整数规划问题，并通过一种启发式的贪婪算法解决该问题.为验证本文算法的效率和可靠性，我们将GMSGA和DE算法进行了实验比较.

1 考虑物理版图设计的电路尺寸设计

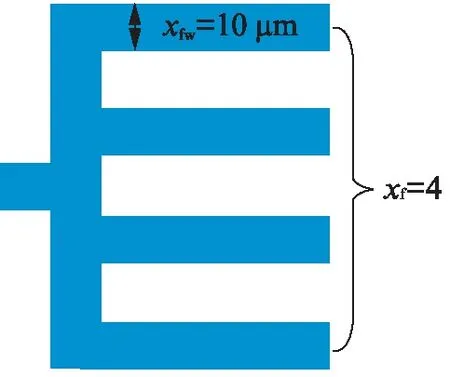
图2 版图物理设计中的MOS管叉指栅结构Fig.2 MOS multi-finger structure in layout physical design

考虑到物理设计的模拟电路设计问题与整数变量密切相关.例如，如图2所示的版图中，MOS管的总宽度xω一般由指宽度(finger width)和指个数决定，xω=xfω⊗xf，其中：xfω和xf分别代表指宽度向量和指个数向量；⊗代表向量对应项乘积.图2中xω=xfω×xf=10μm×4=40μm.为了将版图设计考虑进来，原先基于优化问题的连续设计变量x将分为xfω和xf两部分，其中前者为连续变量集，后者为整数变量集.再如，设计空间的MOS管的倍数变量(multipier)M也是整数.事实上，晶体管的长和宽并非连续变量，迫于工艺的最小线条限制，在考虑物理设计后，MOS管的尺寸是以最小尺寸为基的离散变量，但大部分自动化设计工具将其看作连续变量优化后取整处理.然而，当某些性能指标对输入变量的变化较为敏感时，对于输入变量的上下取整操作可能显著地改变电路性能，从而造成优化结果失效.该问题在高维情况下更容易凸显，因为大量变量的上下取整操作使输入变量值与原值在输入空间上产生明显偏移.

2 问题描述

在基于优化的尺寸设计方法中，模拟电路设计问题被描述如下：

s.t.x∈Dn；

(1)

gi(x)≤0i∈J.

式(1)中： 目标函数f(x)表示模拟电路的目标性能(performance)，或者性能系数(Figure of Merit, FOM)，不失一般性，我们假设优化目标是使FOM最小化；在约束关系中，x表示设计参数，如MOS管的宽和长，电容或电阻的尺寸等；这里n维的x变量形成了设计参数空间Dn，设计空间Dn是由人工设定的合理设计参数输入范围，Dn⊂Rn；gi(x)表示电路性能的非线性约束，由电路的设计指标(specification)决定，这样性能指标形成了性能指标空间；J表示约束序列号集合.

我们可以定义在设计空间x∈Dn内的可行域F≡{x∈Dn|∀i(gi(x)≤0)}，它表示所有满足性能指标约束的设计点x所构成的集合，F⊆Dn.优化目标是： 在可行域F中寻找目标性能f(x)的最优点，即在满足性能指标约束的设计点集中寻找使得目标性能达到最优的设计点.然而不同于传统的优化问题，对于电路设计问题来说，式(1)中的这些函数都是未知的非线性的黑盒函数，这些函数关系由仿真得到.当考虑到物理设计约束时，模拟电路设计问题将变为如下新的形式：

s.t.xd∈Dm∩Nm，xc∈Dn-m；

(2)

gi(xd,xc)≤0i∈J.

式(2)中： 目标函数f依然不变；但在约束关系中，xd代表了离散型变量(discrete variable)，而xc代表了连续型变量(continuous variable)；Nm是m维的整数空间.相对于式(1)的原优化问题，式(2)中设计变量空间由原来的n维连续型变量设计空间分离为两部分：m维的整数空间xd∈Dm∩Nm和n-m维的连续空间xc∈Dn-m.该优化问题变为混合整数非线性规划(Mixed-Integer Non-Linear Programming, MINLP)问题.我们将在第3节提出一种启发式算法来解决该问题.

3 启发式混合整数规划算法

本节我们提出了一种启发式算法以解决式(2)的MINLP问题.该算法大致分为以下3步： 1) 在设计空间中产生起始点；2) 固定连续变量，从起始点开始，利用贪婪整数规划方法仅优化整数变量部分；3) 固定离散变量，使用成熟的非线性约束优化方法序列二次规划(Sequential Quadratic Programming, SQP)完成余下连续变量的优化.

3.1 起始点的生成

本文从多个起始点出发完成局部优化进而达到全局优化的目的，良好的起始点对于局部优化来说至关重要.因此，起始点的生成方法非常关键.首先我们采用侵犯约束权重和(sum of weighted constraint violation)的方法量化地评估起始点的优劣：

(3)

所谓侵犯约束，即不满足约束且超出约束边界的数值大小.这里式(3)进行了归一化处理，其中yi(x)代表约束的函数部分，而Yi代表约束的边界值.特别地Yi=0时，可以归一化yi(x)使其离Yi=0不是太远，然后去掉分母项.式(3)分为两部分： 前者I+表示yi(x)≥Yi时超出约束边界的归一化差值，后者I-表示yi(x)≤Yi时超出约束边界的情况.可见满足约束时对应的归一化差值项为负数，不满足约束时对应的归一化差值项为正数.因此这里，υ(x)值越大，表示超出约束边界的归一化加权和越大，也就表示起始点越不满足约束.

我们首先采用了一种伪随机低差异序列Sobol[6]的方法产生大量的采样点集.与纯随机(random)序列相比，Sobol序列能够在相同空间内产生更加均匀分布的点，这样避免了后期局部优化的群聚现象，增加了优化的空间探索性，即优化搜索的广度.然而，由于Sobol采样在空间上的分离性，纯粹利用Sobol采样得到υ(x)值较小的点，即满足约束程度更好的起始点，需要耗费大量的仿真次数.为了进一步提高采样效率，这里我们提出了一种混合高斯(Gaussian mixture)采样的方式，基本思想是在υ(x)较小的点周围进行高斯分布采样.首先，人工地定义2个υ(x)的边界υsp和υa，前者代表良好与较好起始点的边界，后者代表较好起始点与较差起始点的边界.这样，空间被分为3部分： 良好起始点集Xsp={x|υ(x)≤υsp}，较好起始点集Xp={x|υsp<υ(x)≤υa}，和较差起始点集Xu={x|υ(x)>υa}.显然点集数目N(Xsp)≤N(Xp)≤N(Xu)，即采样较好的点比采样较差的点更难.我们采用利用较多的Xp得到难以获得的Xsp的思路.给定一个点xμ∈Xp，和一个离其最近的较差点xσ∈Xu，其第d维的间距Δxd=|xμd-xσd|，建立高斯分布为N(xμ,Δxd).通过采样这样的高斯分布，我们可以人为地在较好点集Xp附近产生更多的采样点，扩大Xp的采样次数，提高采样得到Xsp点集的概率.考虑到良好起始点的区域可能存在多个，我们建立拥有Ngm个组分的混合高斯采样.最终，我们利用建立的混合高斯采样模型采样得到一个新的采样点，重复上述过程，直至得到需要的N(Xsp)为止.这里我们所使用的混合高斯采样方法的具体算法如图3所示.

3.2 混合整数规划的贪婪算法

传统的解决混合整数规划问题的算法，诸如广义Benders分解法[7]和外逼近算法[8]等，它们固定离散变量xd并求解余下的非线性规划(Non-Linear Programming, NLP)的子问题.

s.t.xc∈Dn-m；

(4)

图4 固定离散变量情况下的二维连续变量空间的局部优化Fig.4 Optimize two dimension continuous variables locally with discrete variables fixed

s.t.xd∈Dm∩Nm;

(5)

s.t.xc∈Dn-m;

(6)

为解决上述式(5)和(6)中的两个子问题，我们分别利用一种启发式整数规划算法和序列二次规划SQP算法.启发式的整数规划算法利用贪婪的策略渐进地固定离散空间的每一个维度，使得每次固定一维后目标函数的数值有所提升.而SQP算法通过解多个二次规划子问题，快速地进行非线性约束和非线性目标的优化，收敛于满足约束的局部最优点.

3.3 局部整数规划的贪婪算法和连续变量的SQP算法

1: 起始点x初始化2: 计算利润值p(x)3: 维度向量Xd←{xi,i=1,…,Nd}4:repeat5: 初始化二维空收益矩阵R6: for all维度xi∈Xddo7: for all每一维度xi的离散决策点xi,jdo8: 记当前决策点xi,j时对应的总变量为xt9: 评估利润p(xt)10: 将p(xt)记入Ri,j11: end for12: end for13: 选出当前收益矩阵R中使p获得最大提升的xi,j,固定第i维度xi←xi,j14: 从Xd中去掉固定的维度xi15: untilXd=∅

我们提出的局部整数规划的贪婪算法的具体流程如图5所示.其中，首先将x的每一维度xi记入维度向量Xd.该贪婪算法的基本思想是渐进地固定离散空间的每一个维度xi，使得每次固定一个维度后xi，目标函数的数值有最大的提升.每经过一次迭代，寻找第i个维度的第j个离散决策xi,j使得目标比当前值更优，然后选出使比当前值最优的离散决策情况，固定这个维度，即维度向量Xd去掉一列.假设一个整数规划问题为Nd维，每个维度上有Na个离散决策点.每次迭代过程中，我们遍历所有可能的决策点，找到一个维度上的一种决策使得比当前值更优且最优，然后固定该维度.为此在这里，我们定义一个利润值p(xt)计算每次在一个维度上选定某个离散决策值时获得的收益，并记入收益矩阵R中.通常的优化过程，在约束不满足的情况下，先优化约束使之满足，然后优化目标函数使之最优.因此，在没有满足约束的可行点时，收益值p(x) 代表的是侵犯约束权重和的减小量，即使约束更加贴近满足；而在有至少一个满足约束的可行点时，收益值p(x) 代表的是目标函数的减小量，即使目标函数更加小.最终可以算出，该贪婪渐进的算法在第i次迭代的仿真次数为(Nd-i+1)×Na次，因此总复杂度为O(N2)，其中N代表混合整数变量中离散维度的大小.这样的复杂度，对于每一次评估都需要调用仿真的电路自动化优化方法是合理的.随着渐进地固定离散空间的每一个维度，当所有整数变量的维度都被固定后，INLP问题的贪婪算法求解过程完成，即收益矩阵R的列数变为0，或者xi维度向量Xd变为空集，如图5所示.

我们采用序列二次规划SQP算法解决余下的连续变量的非线性约束优化(6)子问题.SQP算法是一种成熟的解决非线性约束的局部优化算法，其输入变量为一定边界范围内的连续变量.通过迭代地求解一系列二次规划子问题，SQP算法可以迅速地在约束内寻找到局部最优解.SQP算法可以在数学上保证在约束内的局部优化的最优性，而且最优解一定在约束范围之内.

表1 运算放大器设计变量的信息

4 实验结果及分析

本节我们利用前几节提出的算法设计一个ADC中的2阶运算放大器和一个E类功率放大器.为了验证上述提出算法的效率，我们对比了差分进化DE算法[5].最终我们提出的算法GMSGA，以更强的鲁棒性，在相同的仿真次数下以更好的优化结果，在考虑物理设计规则的前提下完成了这些模拟电路的尺寸设计.

4.1 运算放大器的尺寸设计

运算放大器是模拟电路中最常见的基本单元.图6展示了一个位于ADC中的带有增益提升结构的二阶运放电路，电路工艺为65nm TSMC，我们用该电路验证算法的可靠性.其中Cc1，Cc2，Cc3，Cc4是4个米勒补偿电容.其中Vb3共模反馈的偏执电压未在图6中显示，Vfb1是反馈电压.

图6 带有增益提高结构的运算放大器Fig.6 Operational amplifier with gain boosting structure

如表1所示，其给出该运算放大器的部分设计变量的基本信息.其中，MOS的叉指数f均被设定为整数，指的宽度和MOS管的倍数是固定的.其余变量如电容和偏置电压被设定为连续变量.总问题有25个独立变量，其中17个为整数变量，8个为连续变量.为降低维度和简化问题，其中一些MOS管利用对称结构选用相同的设计变量，且所有MOS的长度均是固定值.本次例子中的仿真工具是HSPICE.

该电路的设计性能目标和性能指标如表2的前两列所示.有效位数(Effective Number of Bits, ENOB)是评估ADC的重要指标.这里我们对运放进行瞬态仿真，然后利用快速傅里叶变换FFT(Fast Fourier Transformation, FFT)分析得到ENOB.我们的目标是最大化100MHz下的ENOB，同时限制1GHz 的ENOB大于9.其余常见的指标如增益(gain)，相位裕度(Phase Margin, PM)，单位增益带宽(Unit Gain Bandwidth, UGB)，最大输出电压Vmax，功耗(power)均被设定为对应的约束条件.

表2 运算放大器的性能指标和优化结果

表3 2种算法之间的优化比较

我们方法得到的一组电路性能如表2第3行所示.得到该组数据共需要1921次SPICE仿真.为了验证算法的效率，我们与差分进化算法DE进行了比较.DE是一种启发式的性能极佳的收敛快速的全局优化算法，我们将部分输入变量进行取整操作以完成混合整数规划，这里称之为Rounded DE.实验总共进行5次，最终Rounded DE在2000次仿真内仅有1次找到了满足约束的解；而得益于混合高斯采样，我们的算法在2000次仿真的设定条件下，有4次找到了满足约束的解.这里，Rounded DE算法表现出不稳定性；而我们的算法，在其中的4次实验中均在1000次仿真时找到了至少一个满足约束的解.最终，在2000次仿真内，我们算法的平均优化结果(9.72)比Rounded DE更好(9.11).这证明了我们算法的高效性和强的鲁棒性.

4.2 E类功放的尺寸设计

如图7所示，该电路结构是一个E类功率放大器[10]，仿真工艺为TSMC 180nm RF，仿真工具为HSPICE.其中，为贴近真实情况，电感器件是带有寄生电阻的模型.如表4所示，其给出了部分设计变量的基本信息.这里，MOS晶体管的宽和长均是固定的，我们只修改晶体管的倍数M，即M1，M2，M3为整数变量.其余的变量包括电容和电感值，设定为连续变量.这样的问题是3个整数变量，9个连续变量的混合整数规划问题.

图7 共栅极E类功率放大器[10]Fig.7 Common gate class-E power amplifier[10]

表4 E类功放设计变量的信息

表5 2种算法之间的优化比较

这里，我们关注两个性能指标： 输出功率Pout和输出效率(Power Added Efficiency, PAE).我们的算法利用高斯混合采样的方法用122次仿真得到了3个良好起始点.然后，利用局部整数规划的贪婪算法从3个起始点出发优化，共仿真110次，得到了3组PAE，其中最好的为0.46.最后每个起始点通过SQP算法都有一定的提升，通过230次仿真得到了PAE为0.51的最优解，Pout为0.62W.与差分进化算法DE的比较结果如表5所示.在500次总SPICE仿真数设定的前提下，总共进行5次实验，Rounded DE算法仅有2次找到满足约束的解，而我们的算法全部找到满足约束的解.并且，平均意义下我们算法的PAE优化结果(0.503)比Rounded DE更好(0.479)，如表5所示.

5 结 语

针对考虑物理设计的模拟电路自动化尺寸设计问题，该问题由原来的连续变量的非线性约束优化问题变成了混合整数非线性规划问题.为了在基于仿真的优化框架下完成自动化尺寸设计，本文提出一种启发式的方法GMSGA将该问题分解为整数规划和连续变量规划两个子问题分别求解，前者利用一种贪婪算法在O(N2)下求解整数部分，后者利用SQP算法求解连续部分.最后为验证算法的可行性和效率，我们设计并优化了一个ADC中的运算放大器和E类功率放大器，与Rounded DE算法相比，我们提出的算法GMSGA稳定性和优化结果都更好： 在相同的仿真次数内进行多次实验，GMSGA以更多的次数地找出满足约束的解，并在本文的实验例子中使优化的均值结果提高约5%.