初始编码及最大序列号均未知时总体容量的估计

李亚男，王昱泉，陈国蓝，胡跃清

(复旦大学 生命科学学院 生物统计学与计算生物学系，上海 200433)

在二战时期，西方盟国主要通过收集情报和统计学方法来估计德国的坦克数量，从而确定敌军的力量.战后获取的有关纪录表明，相较于收集情报法，统计估计的结果与德国实际生产的坦克数量更加接近[1].调查发现，德国坦克的序列号是从1开始连续编码的.因此，如何利用俘获/击毁的坦克的序列号来估计坦克的总体数量，就变成统计学上的参数估计问题： 基于无放回抽样的初始编码为1的总体容量的估计.类似的序列号估计问题在其他场合也常遇到，如二战期间德国的V-2火箭、苏联装备工厂数量的分析以及Commodore 64计算机总数的估计等[1-2].

在之前的研究中，有不少关于德军坦克问题的实际背景和相应的概率模型的描述[3-7]，以及针对它的相关的估计[8].这些探究均是基于无放回抽样的.孙华娟等则在此基础上分别探究了有放回和无放回抽样情况下相关统计量的构建及优劣比较[9-10].不过这些研究均假定坦克的初始编码是1.然而某个时间段某产品的产量问题，也即初始编码未知时总体容量的估计，却极少有人探究.

考虑到大多数实际问题中，样本容量相较于总体容量来说很小，有放回抽样和无放回抽样结果之间的差别可以忽略不计，本文在研究德军坦克问题的基础上，深入探究了在有放回抽样情况下初始编码未知时的序列号估计问题.本文针对性地提出了6种不同的估计量，并设计了一系列的随机模拟，用来直观比较这些估计量的无偏性和均方根误差.结果表明极大似然估计在小样本时偏倚较大；Jackknife法可以有效改善偏倚；迭代法、近似法、区间长度法得到的相应估计量以及无放回抽样时最小方差无偏估计的表现相差不大，估计效果均较好.

1 估计方法

假设总体是{θ1,θ1+1,…,θ2}，θ1和θ2分别是最小和最大序列号，它们均未知，θ=θ2-θ1+1为总体容量.现从中进行有放回抽样，得到简单随机样本X1,X2,…,Xn.不失一般性，设样本容量1≤n≤θ.如何利用样本提供的信息来估计总体中的未知参数的问题[11]，极大似然估计(Maximum Likelihood Estimate, MLE)是常用方法.极大似然估计在1821年首先由德国数学家高斯提出，但当时并没有受到人们的重视.后来，英国统计学家Fisher重新提出并阐述了它的主要内容，因此极大似然估计通常归功于Fisher[12].由样本观察值x1,x2,…,xn，可得似然函数

θ1+S(θ1,θ2),

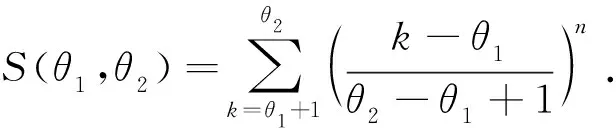
θ1=E(X(1))-S(θ1,θ2),

(1)

θ2=E(X(n))+S(θ1,θ2).

(2)

由于S(θ1,θ2)涉及未知参数θ1和θ2，故无法从式(1)和(2)出发构建θ1和θ2的无偏估计.下面先估计S(θ1,θ2)的大小.对于任意正整数n，有

所以

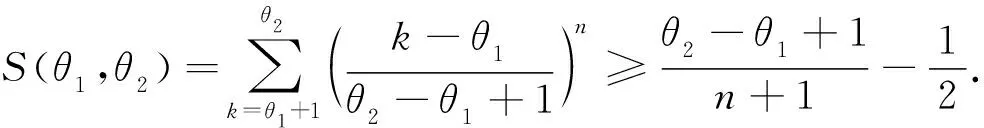
(3)

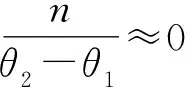
更进一步，

故得总体容量θ的近似无偏估计为

(4)

(5)

这里[·]表示向下取整.下面证明迭代算法(4)和(5)均是收敛的.首先

S(θ1-1,θ2)>S(θ1,θ2),S(θ1,θ2+1)>S(θ1,θ2).

(6)

下面用数学归纳法证明

(7)

由式(4)，(5)和S(θ1,θ2)的非负性知式(7)当i=0时成立.假设式(7)对某自然数i成立，重复利用式(6)可推出

所以由式(4)和(5)可得

因此式(7)得证.接下来用数学归纳法证明

(8)

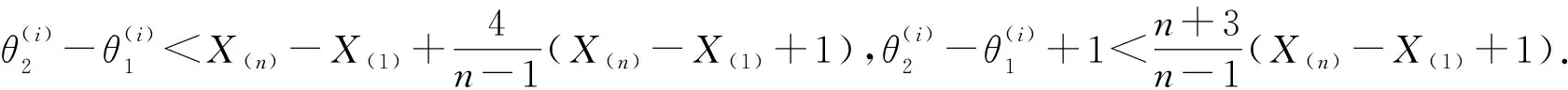
同理，由式(3)和(5)有

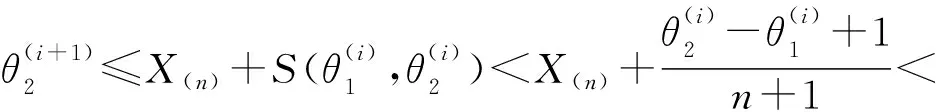
从而得

进而得到总体容量θ的估计

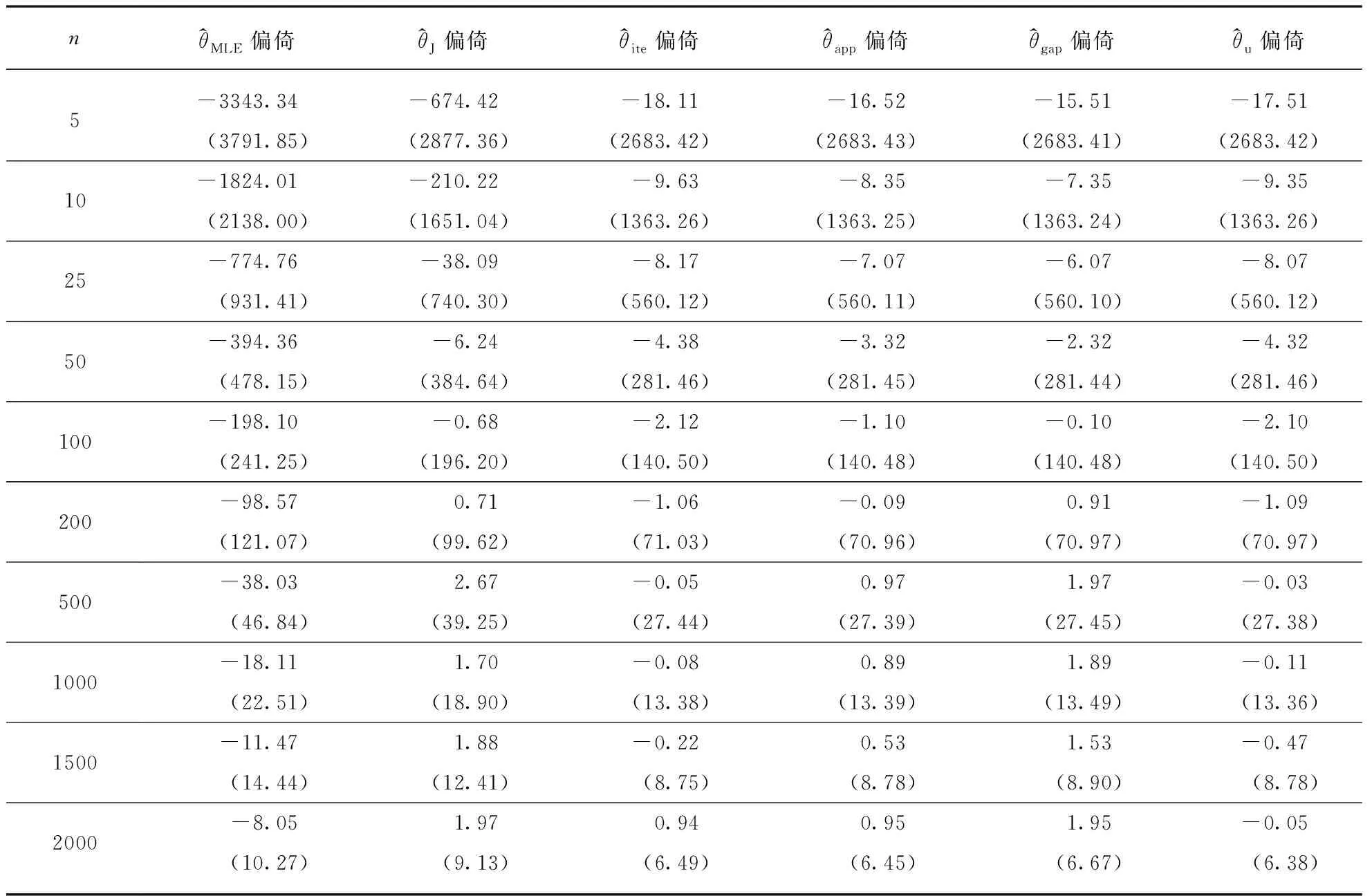
考虑到在实际问题中，抽样往往是无放回的.下面考虑利用无放回抽样获取的样本X1,X2,…,Xn来估计总体容量的问题，为了方便，仍然用X(1)

同样地，对总体做一个反变换后可得

因此，

由此可得总体容量的无偏估计

(9)

同时T1的方差

Var(T1)=E(T1-θ)2=

E(T1-T2+T2-θ)2=

E(T1-T2)2+E(T2-θ)2+2E[(T1-T2)(T2-θ)]=

E(T1-T2)2+Var(T2),

(10)

这是因为E[(T1-T2)(T2-θ)]=E[(T2-θ)E(T1-T2|X(1),X(n))]=0.

(11)

同样地，当θ2=θ1+(n-1)+1时有

由式(11)知上述等号右边的前两项均为零，考虑到P(X(1)=θ1,X(n)=θ1+n)>0，故有

又考虑到θ1的一般性，有

依次类推，我们便有

再次考虑到θ1的一般性，最终有

2 随机模拟研究及实例应用

2.1 模拟设计

2.2 模拟结果

限于篇幅，我们只展示θ=10000的随机模拟结果.表1为有放回抽样和无放回抽样下，n=10，重复次数R分别取不同值时各估计量的模拟结果.从表中可以看出，重复次数R=1000时，各估计量的偏倚较大，这说明了n较小时，如果重复次数不是足够大，模拟结果难以体现各估计量的特性.R增加到10000或以上时，各估计量的均方根误差均趋于稳定，偏倚也接近真实值.

表1 采取有放回/无放回抽样，θ=10000，n=10时，6个估计量的偏倚和均方根误差

表2 采取有放回抽样，θ=10000，随机模拟重复10000次时，6个估计量的偏倚和均方根误差

表3 采取无放回抽样，θ=10000，随机模拟重复10000次时，6个估计量的偏倚和均方根误差

2.3 实例应用

3 总结与展望

其实，本问题只是德军坦克问题的一种简单推广，通过放宽约束条件，该问题有许多理论上的有趣推广，而且大量有价值的实际问题都属于此类序列分析问题.例如在均匀分布总体的容量与总体的分布范围允许不相等的情形下，总体容量和总体分布范围的估计问题： (a) 已知总体容量大于总体分布范围，即存在编号重复，包括大量重复和少量重复.如根据身份证15～17位数字估计当地户籍人口数量等.(b) 已知总体容量小于总体分布范围，即存在编号空缺，包括接近密集和十分稀疏.如借助一个小区域内小汽车的车牌号估计当地汽车总保有量.(c) 总体容量与总体分布范围的关系未知，尤其当两者比较接近.如根据列车或剧院外排队人群的票号估计座位数和总人数.此外，还可以考虑总体分布近似均匀或仅仅存在近线性偏离的情形.如老年人群随机抽样年龄/生日调查以估计最长寿者年龄，或人群随机抽样生日调查以估计人口数量等.

因篇幅所限，且上述问题的复杂性已大大增加，此处不再一一探讨求解.序列号估计问题最初看起来简单直观，但其问题类的推广变形很可能超越我们的预想，对其做进一步理论探讨无疑是很有必要的.后续我们希望对推广问题提出更多种类的估计和求解方法，再佐以随机模拟和真实数据试验，追求达到更深刻、完整的认识.