基于Adaboost-CART模型的动卧列车客座率预测

王煜，方伟，王亮，薛冰

（1.中国铁道科学研究院集团有限公司 电子计算技术研究所，北京 100081；2.中国国家铁路集团有限公司，北京 100844）

0 引言

近年来，动卧列车已成为高铁旅客运输中颇受欢迎的一种运输产品[1]，培育了一批“忠实”的旅客群体，整体客座率较好。随着铁路运输企业逐渐向市场化运营靠拢，实施了更加灵活多变、有针对性的开行方案和票价方案[2-3]，对动卧列车客座率进行预测便成为铁路运输企业优化运输资源配置、提升运输效率、实现更大经济效益的必然要求和重要支撑。因此，动卧列车客座率预测具有较强的实际指导意义。

目前，对高铁动车组列车客座率预测研究较多，不同学者采用多种模型方法进行预测，如多元回归模型、时间序列模型[4-5]、神经网络模型[6]、决策树模型、灰色理论模型[7-8]、集成学习算法模型等[9]。每种模型各有优点，但也存在一定局限性：多元回归模型和时间序列模型以统计学理论的线性算法为基础，对样本数量和质量要求较高，对非线性数据预测结果较差；神经网络模型较复杂，容易陷入局部极值，当样本量过小时很难提高训练准确率；单一使用决策树模型在小样本情况下容易产生欠拟合，且剪枝条件等参数较难确定。综合考虑以上因素，采用Adaboost集成学习算法对CART模型进行优化，建立Adaboost-CART模型，克服单一CART模型在数据样本过小情况下精度不足的问题，提高单一CART模型的准确性，并应用于动卧列车客座率预测。

1 Adaboost-CART模型原理

1.1 CART模型及特征选择

决策树模型是通过一系列规则对数据进行分类或回归的过程，判断依据是样本数据的特征值，如果不考虑效率等因素，样本所有特征的判断终会将某个样本分到一个类上。实际上，样本所有特征中有一些特征在分类时起到决定性作用，决策树的构造过程就是找到这些具有决定性作用的特征，根据其决定性程度构造1个倒立的树，决定性作用最大的那个特征作为根节点，然后递归找到各分支下子数据集中次大的决定性特征，直至子数据集中所有数据都属于同一类。

CART模型属于决策树模型的一种，在信息熵（ID3）、信息增益比（C4.5）等传统特征切分准则基础上，采用基尼系数（Gini系数）来选取合适的特征作为切分节点，通过二元递归分割的方式形成一个优化的二叉树，进而实现分类或回归。Gini系数是对当前特征不纯性的度量，该特征包含的类别杂乱度越低，Gini系数就越小，优先选择Gini系数小的特征作为分类特征。假设有K个类别，第k个类别的概率为pk，则Gini系数表达式为：

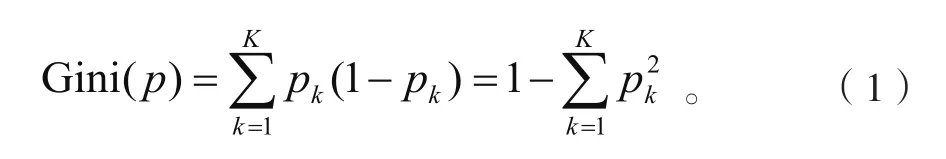
为简化计算，CART模型每次仅对某个特征的值进行二分，而不是多分，这样建立的是二叉树，相应Gini系数表达式为：

CART分类树输出结果为离散值，当使用CART模型输出样本为连续值时，便是CART回归树，此时采用方差的方式选择特征和特征值划分点。CART回归树中任意划分特征A，对应任意划分点s两边划分的数据集为D1和D2，求出使D1、D2集合的方差和最小时的特征和特征值划分点，表达式为：

式中：c1为D1数据集的样本输出均值；c2为D2数据集的样本输出均值；A为任意特征；s是特征A的一个划分点；xi为样本值；yi为模型输出值。

1.2 Adaboost集成学习算法

CART模型具有很强的泛化能力，受到异常数据影响较小，但与所有大样本统计方法相同，当样本量较小时模型不稳定。使用Adaboost集成学习算法能够使CART模型重复使用样本数据，并通过集成多个CART模型做出最终预测，不仅提高了准确率，还增强了CART模型处理小样本数据的稳定性，从而改进预测效果。以CART模型作为弱学习器，利用Adaboost集成学习算法对多个CART模型进行集成，最终组合成一个强学习器，并利用该强学习器预测动卧列车客座率。

Adaboost集成学习算法是Boosting算法的一个分支，先训练出1个弱学习器，根据结果误差率更新样本的权重，增加误差率高的样本的权重，根据调整权重后的样本训练出第2个弱学习器，如此迭代循环，直到训练出T个弱学习器，最终通过集合策略将这T个弱学习器进行整合，成为一个强学习器。主要步骤为：

（1）假设有样本集T={（X1，Y1），（X2，Y2），…，（Xm，Ym）}，弱学习器G（x），将样本集T带入G（x）训练，迭代次数为K。

（2）初始化样本集权重D1=（W11，W12，W13，...，W1m）。

（3）使用具有权重Dk的样本集进行训练，得到弱学习器Gk（x）。

（4）计算训练集的最大误差Ek=max| yi- Gk（xi）|，i=1，2，…，m。

式中Zk为规范化因子，

（9）重复上述过程，设定迭代次数阈值，最终组合成强学习器，该学习器为f（x）=∑akGk（x）。

2 实例应用

2.1 特征选择与样本数据

旅客列车客座率的影响因素主要有季节周期、旅客需求变化、价格需求弹性、宏观经济影响等。目前，

我国动卧列车开行区间主要为京沪、京广（深）、沪深、沪西、京昆等[10]，运行距离较长，主要竞争对手为同区间的航空客运。短期来看，航空票价水平直接影响动卧列车的客座率。航空票价随预售期、航班种类、机型、附加服务等的不同而动态调整。选取某个固定的价格指标或某个时点的价格指标作为参考基准代表性较差，通过大量跟踪统计发现，经济舱比其他舱位更具有价格代表性，可以反映航空票价的整体水平。

因此，在整个预售期内，每隔固定时间对所有航班经济舱最低票价进行一次记录，并计算出记录时刻对应始发日期的经济舱最低票价的平均数、中位数、众数3个指标。最后，将最终时刻（选取始发日期的前一天）的经济舱票价平均数、中位数、众数和当日动卧列车票价水平确定为Adaboost-CART模型的4个特征指标。将选取的样本数据输入CART模型，按照均方差最小的原则对上述4个特征指标进行连续二分，最后形成1个倒立的二叉树模型，即CART回归模型。此时CART回归模型是一个弱学习器，容易导致过拟合，因而预测精度不高。按照Adaboost集成学习算法原理，对该CART回归模型进行迭代优化，每次迭代时通过增加误差较大的样本的权重，产生一组新的训练样本，将新的训练样本输入CART模型重新训练，产生新的学习器，最后综合考虑迭代次数和误差率，将所有学习器按照权重组合为一个强学习器，并对动卧列车客座率进行最终预测。

样本数据方面，选取116 d的数据（116组数据）作为研究对象，形成116×5的数据矩阵，其中，前4列为每个样本对应的4个特征指标，最后1列为对应的动卧列车客座率（以京沪动卧列车为例）。京沪动卧列车日客座率分布见图1，可看出动卧列车日客座率主要集中在60%～80%，其次为40%～60%。动卧列车客座率最低为16.9%、最高为95.3%，中位数为66.3%，平均值为65.3%。

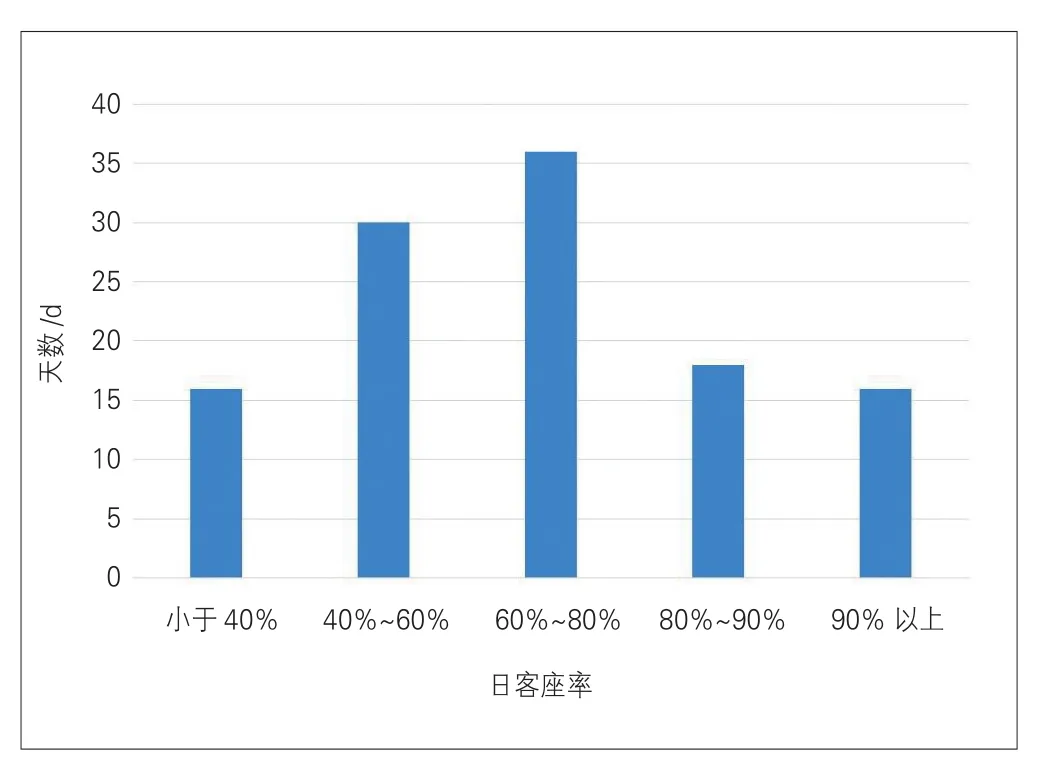
图1 京沪动卧列车日客座率分布

2.2 训练模型

利用前100组样本数据训练Adaboost-CART模型，后16组样本数据进行模型检验。通过参数的反复调整，确定迭代次数为500、学习率为0.5时达到相对误差最小的目标。前100组样本数据拟合结果与实际值对比见图2。

图2 前100组样本数据拟合值与实际值对比

2.3 结果分析

利用训练好的模型对后16组样本数据进行预测，并比较预测值与实际值（见图3）。为便于比较和分析，同时采用单一CART模型和多元回归模型进行预测，结果见表1。其中每个样本的预测误差由|预测值-实际值|/实际值×100%计算得出，误差平均值为16个样本预测误差的算术平均值。

图3 Adaboost-CART模型预测值与实际值对比

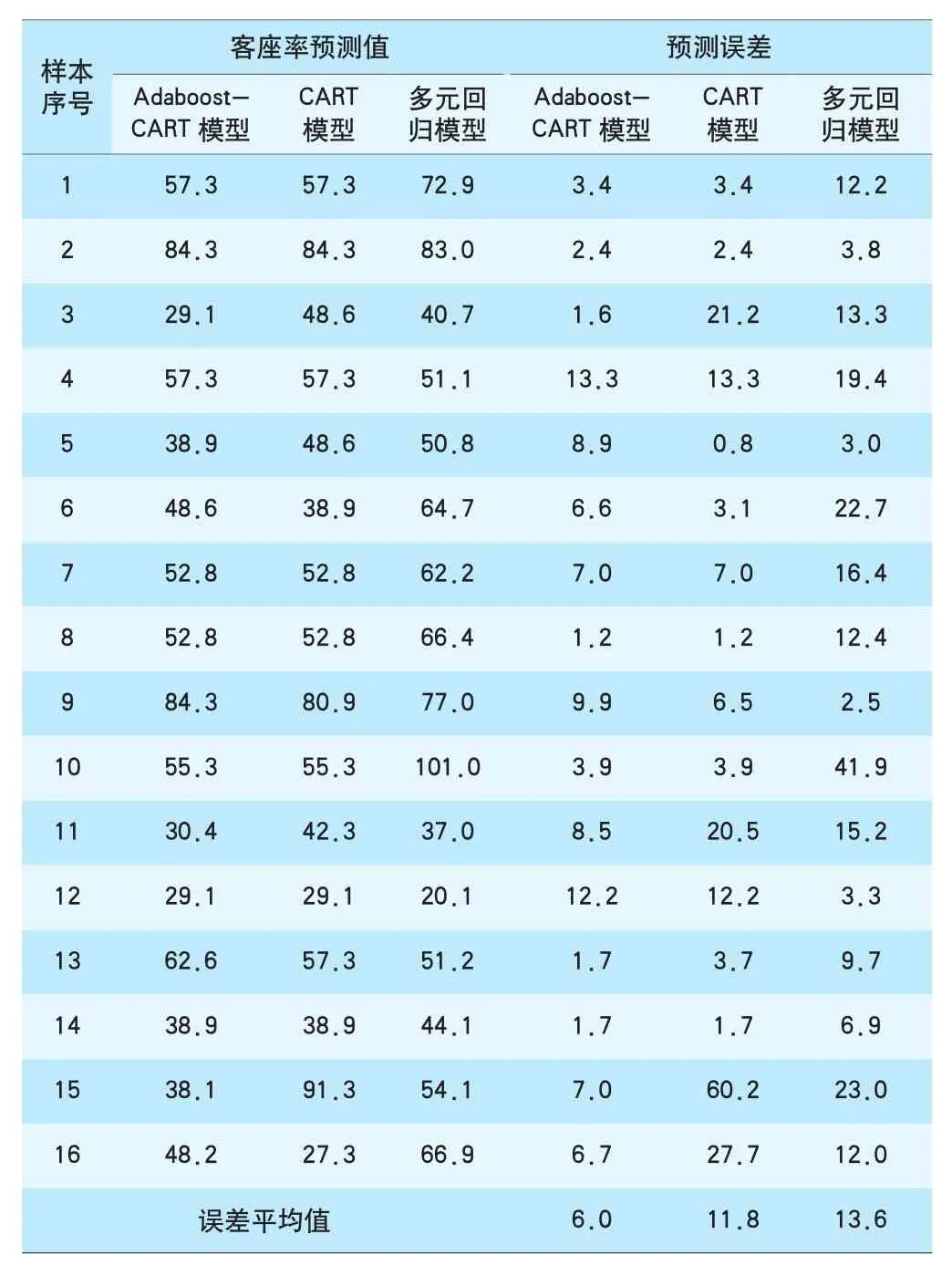
表1 不同模型预测结果 %

由图3和表1可知，基于Adaboost-CART模型对京沪动卧列车客座率预测的误差平均值为6.0%，显著小于单一CART模型的11.8%和多元回归模型的13.6%，说明Adaboost-CART模型有较高的准确率。

Adaboost集成学习算法的核心是通过不停的迭代优化弱学习器，将几个弱学习器最终组合成一个强学习器。为了研究迭代次数对模型预测精度的影响，进行了20次试验。在学习率为0.5的基础上，第一次试验迭代次数为50次，第二次试验迭代次数为100次，以此类推，最后一次试验迭代次数为1 000次。计算每次试验的误差率（见图4），可知，随着迭代次数的增加，预测结果的误差率迅速下降，在迭代次数为500次时达到最小，同时，迭代次数超过200次后，预测结果误差率基本稳定在一个范围内，上下波动。由此也进一步验证，Adaboost-CART模型比单一CART模型在预测精度上有优势。

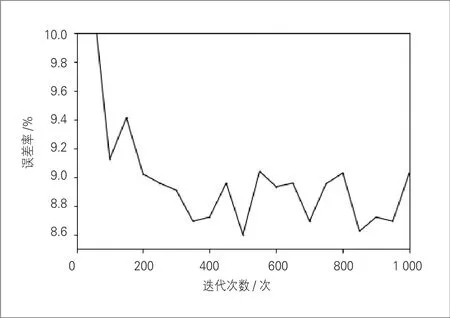
图4 迭代次数与误差率关系

迭代次数的增加也意味着模型变得更复杂，需要消耗更大的计算能力。因此，需要根据实际情况合理确定迭代次数，实现计算复杂度和精度的平衡。

3 结论

以CART模型作为弱学习器，采用Adaboost集成学习算法进行集成，通过调整样本数据权重和不断迭代，对弱学习器持续改进，最终训练出一个强学习器。

按照固定的时间间隔对京沪区间航空经济舱最低票价进行统计，计算出对应每个始发日期航空经济舱最低票价的平均数、中位数、众数，并与京沪动卧列车票价一同作为特征值输入训练后的模型，对动卧列车客座率进行预测。结果表明：采用Adaboost-CART模型能够较好地对动卧列车客座率进行预测，且预测效果相比单一CART模型、多元回归模型有较大提升，验证了所提出模型的有效性和可靠性。

随着迭代次数的增加，模型预测误差率快速下降，但达到一定迭代次数后，误差率稳定在一个区间范围内，上下波动。随着迭代次数的增加，模型的复杂程度和所需的计算量也相应增长，如何选择迭代次数与模型精度的平衡点需要进一步研究。