研究通性通法，突出高中数学核心和本质

江苏省苏州市吴中区甪直高级中学 冯中芹

在高中时期，数学是比较难学习的一门课程，无论是学习文科还是学习理科，都会有一部分同学的数学成绩不是很理想。造成这种现象的主要原因其实就是没有掌握数学的理念以及衍生的基本数学运算技能，在这一点上，师生双方都有一定的不足，针对如今这种现象，研究通性通法在高中数学中得到了运用，而且根据相关专家和学者的调查来看，研究通性通法在高中数学中的应用已经取得了一定的成效。本篇文章的主旨就是研究通性通法，突出高中数学核心和本质。

一、通性通法的内涵

例如，在当前的数学高考试题中，圆锥曲线问题往往会与直线方程相结合，在解题过程中，需要高中生把直线方程代入圆锥曲线方程中，这样便能整理成为一个一元二次方程，此时那些简单的数学知识就能得以运用了，例如判别式、求解公式、多个解与系数的关系等等，相关的专家和学者往往就利用这些简单的知识编出许许多多精彩的数学试题。其实一道数学题可能会有多种解题方法，有些同学往往希望通过自己的学习掌握一道题目的多种解题方法，但是实际上高考数学往往淡化了一些特殊的解题技巧，因为这些特殊技巧的掌握其实会消耗老师和同学的很多时间，所以说刻意去追求特殊的解题方法并不是很好的选择。

二、通性通法的大致特性

对于通性，我们可以这样理解：如果满足一切相关的知识理论，就归纳为通性。但这个概念过于笼统，如果将适合的理论概念全部涉入，也会使得“通性”这个概念变得繁重且复杂，所以，在这里我们对这些条件和理论进行区分和化解。首先，这些理论或者是知识、结论，对于教师和学生来说必须都是非常熟悉的、能够通过学习去理解的，从这一点我们便不难看出，“通性”是具有熟知性的。此外，“通性”中的理论知识应该能够直接采用，并且在采用之后的能够解决一系列的问题，而不是在特定情况下，这些理论知识才能去应用，这无论对于教师还是高中生，都是十分不可取的。最后，“通性”一定要具有普遍性，理论知识的涵义必须是清晰的，不能让学生或者教师理解起来是存在歧义和争论的，这种普遍性我们也可以将其理解成为确定性质。

对于通法，我们则可以这样理解：字面意义上来解释，“通法”即是能够解决一类问题的方式方法，从某种意义上说就是“通性”结论产物，在泛指的意义上来说，通法是指解决问题的方法的一类。根据相关学者和专家的研究发现，通法可以适用于一类的问题上，所以，“通法”具有适用性。另外，“通法”是“通性”的衍生物，所以它对“通性”的依赖性很强，但是在熟练运用之后，我们就可以单独采用“通法”而不用再去“通性”中验证一番，所以，在一定程度上“通法”是具有有序性的。最后，因为时代在不断发展，数学高考也要顺应时代进行发展和改变，因此“通法”还要适应时代进行一定的升级和改变，但是“通法”在整体上还是适用的，故而“通法”还具有一定的稳定性质。

三、通性通法理论的初步界定

通过上述文章中对通性通法进行拆分理解，其实我们就很容易对二者进行理解了。对于现阶段的通性通法，我们依然没有对其进行整体界定，这不仅仅是因为通性通法在时代中是不断进化和发展的，而且还因为通性通法的范围比较宽泛，其不仅可以涉及高中数学，还涉及其他的学科，甚至还能涉及其他的学术范围中。经过多年的研究，许多专家和学者凭借丰富的知识已经对其进行了初步的界定，其发挥的作用是令每一个人都想不到的。接下来我们将对此进行详细阐述，由于其在高中数学的表现比较明显，我们将以江苏省2017 年的高中数学试题作为例子进行参考。

例如，2017 年江苏省数学高考试题的填空题第三题：某工厂生产甲、乙、丙、丁四种不同型号的产品，产量分别为200，400，300，100 件，为检验产品的质量，现用分层抽样的方法从以上所有的产品中抽取60 件进行检验，则应从丙种型号的产品中抽取_____件。

同张试卷的必做题二十三题：已知一个口袋有m个白球，n个黑球（m,n∈N,n≥2）,这些球除颜色外全部相同。现将口袋中的球随机逐个取出，并放入如下所示的编号为1,2,3，……，m+n的抽屉内，其中第k次取球放入编号为k的抽屉（k=1,2,3，……，m+n）。

1 2 3…m+n____

（1）试求编号为2 的抽屉内放的是黑球的概率P；

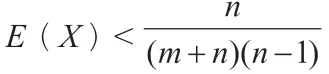
（2）随机变量X的概率分布为：

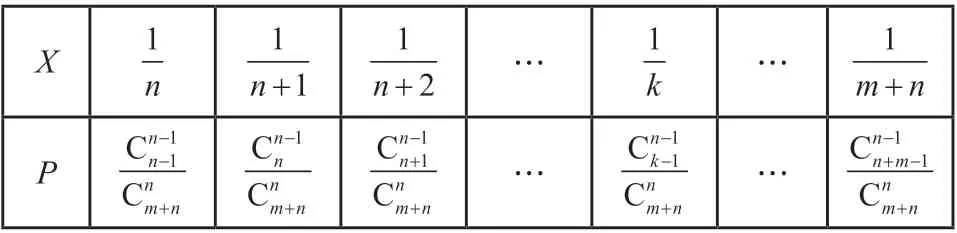
X images/BZ_8_1614_2546_1631_2563.pngimages/BZ_8_1737_2546_1753_2563.png……images/BZ_8_2226_2546_2243_2563.pngP ……

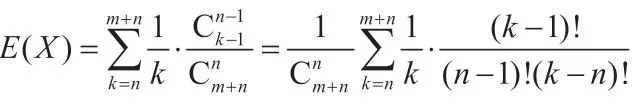
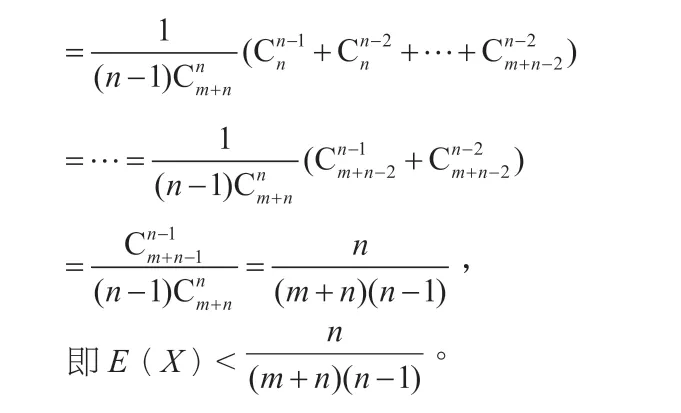
这两道高考数学题考查的是古典概率、随机变量及其分布、数学期望等基础知识，第一道填空题比较简单，只是考查了简单的概率问题，后一道大题就考查了组合数及其性质, 考查运算求解能力和推理论证能力。两道题固然在本质上有一些不同之处，但是可以用通性通法的方法解决，因为两道题是互相关联的。另外，学生在高考这样重大的考试中难免紧张，都有可能一时忘掉其解法，这时学生如果熟知通性通法的基本概念，就可以由其中一道题推算出另一道题目的解法，而且，后一道大题这里只给出了一种解法，学生还可以通过向公式代入数值的方式进行解答。所以说如果能将通性通法进行一定的界定，对于学生的数学知识掌握是大有裨益的。

众所周知，笛卡儿所创立的解析几何思想可以说是整个数学界发展过程中的一次巨大飞跃了，通过将坐标和方程结合的方式，使得代数与几何图形完美地结合在一起，这种方式不仅充分发挥了几何直观形象以及能够进行推理演算的优势，还能够将代数精确运算的价值运用其中，大大节省了解决数学问题的时间。由此可见，几何思想是数学通性通法的具体表现。这一点从江苏省数学高考试题的18 题中便够体现出来：

如图1，水平放置的正四棱柱形玻璃容器Ⅰ和正四棱台形玻璃容器Ⅱ的高均为32cm，容器Ⅰ的底面对角线AC的长为10 cm，容器Ⅱ的两底面对角线EG，E1G1的长分别为14cm 和62cm。分别在容器Ⅰ和容器Ⅱ中注入水，水深均为12cm。现有一根玻璃棒l，其长度为40cm。（容器厚度、玻璃棒粗细均忽略不计）

（1）将l放在容器Ⅰ中，l的一端置于点A处，另一端置于侧棱CC1上，求l没入水中部分的长度；

（2）将l放在容器Ⅱ中，l的一端置于点E处，另一端置于侧棱GG1上，求l没入水中部分的长度。

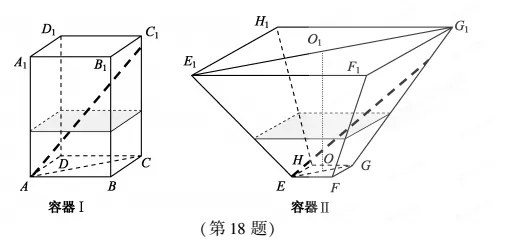
图1

如图2，记玻璃棒的另一端落在CC1上点M处。

记AM与水面的焦点为P1，过P1作P1Q1⊥AC，Q1为垂足，

则P1Q1⊥平面ABCD，故P1Q1=12，

答：玻璃棒l没入水中部分的长度为16cm。

( 如果将“没入水中部分”理解为“水面以上部分”，那么结果为24cm)

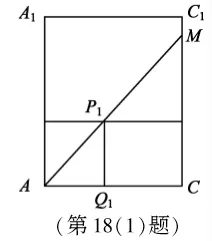
图2

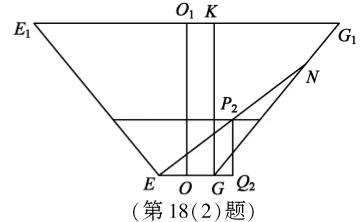
图3

（2）如图3，O，O1是正棱台的两底面中心.

由正棱台的定义知，OO1⊥平面EFGH， 所以平面E1EGG1⊥平面EFGH，O1O⊥EG。

同理，平面E1EGG1⊥平面E1F1G1H1，O1O⊥E1G1。记玻璃棒的另一端落在GG1上点N处，

过G作GK⊥E1G，K为垂足， 则GK=OO1=32。

因为EG= 14，E1G1= 62，

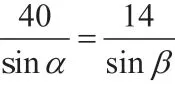
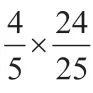
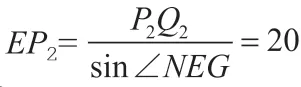
答：玻璃棒l没入水中部分的长度为20cm。

在这道题目中，两个容器便是几何图形，其中对于情境的变化时时刻刻在牵动着数学通法的改变。这道题目中的几何图形都有着很好的几何性质，所以与其相关的数学问题可以借助平面几何知识来解决，而当这些图形组合演变成一个几何体时，就要依靠我们比较熟悉的代数运算的力量了，这道题目中的代数运算可以研究几何图形的性质，在解题过程中，学生也利用图形的性质进行简化计算，二者互为共生，体现了数学当中的“数”与“形”的结合。

四、高中数学对于通性通法的外延界定

经过高中数学对通性通法进行了初步界定之后，此后通性通法的发展就有了一定的参照物，发展过程也就变得更加具有方向感。由前文我们不难得知，高中数学知识当中的明确定理、概念以及推论是可以归纳到通性之中的，而这些定理、概念以及推论之下的方法是可以归纳到通法之中的。但是许多公式并不是在定理中或者推论中得出来的，在高中生的日常数学计算中，这些公式的应用非常频繁，因此，这些公式也能归纳到通性通法当中。

五、由通性通法得出的高中数学的核心和本质

一道高中数学题可能会有多种解法，但我们要求的是着重一种解法。在这里许多师生可能会有一定的误解，我们进行详细的解释。一道数学问题是有多种解法的，而这些解法在难度上就会有高有低，有些是运用基本的通性通法的理论知识，而剩下的比较难的方法大多都是需要高中生采用一些不属于通性通法的内容进行解答，但是比较难的解答方式方法的思维过程比较新颖，另辟蹊径，有些同学不易想到。重视通性通法并不是强行学会比较难的解题方法，而是在学会一种基础解题方法的基础上再掌握另一种基础解题方式，切勿还未学会走路就要自行奔跑，这在高中数学的学习上是十分不可取的一种行为。所以，无论是高中生还是高中数学教师，都要重视通性通法，并将其进行应用。

在高中数学中，通性通法的概念已经得到了初步的界定，而在高中数学中应用通性通法的概念，从某一方面来说也是在强调高中数学的重要性，突出高中数学的核心和本质。