高等数学教学中融入思想政治教育刍探
周晓燕


摘 要:学生的全面发展是教育教学的最终目标,教师应该把思想政治教育融入到教育教学活动中。文章探讨高职院校数学教师在高等数学教学过程中如何有效融入思想政治教育,并对学生加强理想信念教育、集体主义教育、诚信教育、人文教育等,以促进学生全面发展,培养学生合作精神、诚实守信等优良品质。
关键词:高等数学;思想政治教育;教学方法;诚实守信;全面发展
中图分类号:G641;G712 文献标志码:A 文章编号:1008-3561(2019)27-0007-02
一、背景
中共中央、国务院发布的《关于进一步加强和改进大学生思想政治教育的意见》特别强调“充分发挥课堂教学在大学生思想政治教育中的主导作用”。思想政治教育从来都不是完全独立于其他学科而存在的,高校中的每门课程都具有很强的育人功能,每位教师都肩负着教书育人的职责。
“高等数学”是大学生的一门基础必修课程,在高等学校教育中有着举足轻重的地位。为此,笔者按照高职教育的人才培养模式及“高等数学”这门学科的要求,结合本校的实际情况,通过调查问卷进行统计分析,并通过开展师生座谈会和教学实践尝试等,研究如何更好地在高职高等数学教学中加强大学生的思想政治教育,把育人工作有效渗透到课堂教学中。
二、研究过程
面向全院开设“高等数学”“计算机数学”“经济数学”等数学类课程的全体学生开展问卷调查。问卷调查的结果显示:81.5%的学生希望教师在上数学课的时候介绍数学发展史;78.2%的学生觉得学习数学可以锻炼他们的创新能力;89.1%的学生认为我国古代的数学家取得了超前于世界其他国家的先进成果;91%的学生喜欢教师利用先进的教学资源及手段开展课堂教学;83%的學生希望教师可以在课堂上开展形式多样的教学活动,如分组讨论、抢答等;98.2%的学生认为数学教师和学校的思想政治辅导员及“两课”教师一样,将影响着他们思想道德的培养与成长;83%的学生认为数学学科的特性,有利于培养他们的抽象思维和缜密概括的能力。
通过认真分析问卷调查结果,并结合师生座谈会及教学实践尝试等,笔者认为,在高职高等数学教学中融入思想政治教育,可以从以下几个方面进行。(1)在日常的课堂上,教师讲授数学知识时要积极引导学生,进行理想信念教育、人文教育,积极引导学生进行思维创新。数学知识中的性质、公理、定理、公式等都是前人及数学家们在客观世界、现实生活中经过种种努力,克服各种困难才抽象概括出来的。教师要通过介绍数学家们积极探求真理的事迹,让学生学习科学家们不畏艰难、勇于求知的精神。教师还要深入探索,发掘数学文化中的人文价值,进而活跃课堂氛围,提高学生学习的积极性。(2)教师在教学中可以采用分组讨论、代表总结等方法对学生进行集体主义教育,让学生分工合作,共同达成学习目标。教师要通过让学生自己思考、小组讨论的形式,提高语言交流的能力。教师要结合学生熟悉的生活事例,让学生与教师及同学共同合作,培养他们主动学习的能力。(3)教师在数学教学过程中要加强诚信教育。数学是一门严谨的学科,教师向学生教授的各种运算性质、各类公式以及定理等都具有很强的逻辑性。因此,教师要把思想政治教育潜移默化地融入数学教学中,培养学生严谨的逻辑思维能力,培养学生实事求是的科学态度,进而使学生形成积极正确的世界观、人生观和价值观。(4)教师在数学教学中要引经据典(古代数学家的成就),激发学生的爱国情感。在数学教学中,教师可将我国的数学史融入课堂教学,介绍相关的古代数学家的成果,使学生树立文化自信,克服崇洋媚外的心理,增强民族自豪感,以自己身为中国人而骄傲。教师还要让学生充分认识到自己的社会责任,传承祖先的文化,勇于担当,进而激发学生学习热情和爱国热情。(5)培养学生理论联系实际的作风,以及数学意识和实际应用能力。数学学科的基本特征之一是其应用的广泛性。随着科学技术的飞速发展和社会的进步,数学不但在各个传统领域(如工程技术、经济建设等)发挥着越来越重要的作用,而且不断地向新的领域(如生物、医学、金融、交通、人口、地质等)渗透。教师通过用数学知识解决学生熟知的日常社会生活中的问题,采用学生容易理解和接受的方式传授数学知识,注重学生的亲身实践,这些都可以增强学生学好数学的信心。
三、教学实例
笔者现以“定积分的概念”课堂教学为例,简要阐述如何在日常的课堂教学中融入思政教育。
1.定积分产生的历史背景——课程引入
预备知识:教师要让学生通过抢答,归纳总结常见的平面图形面积的计算公式(包括矩形、菱形、平行四边形、梯形、扇形等),调动课堂气氛。
案例1:《黄鹤楼送孟浩然之广陵》(唐,李白)故人西辞黄鹤楼,烟花三月下扬州。孤帆远影碧空尽,唯见长江天际流。
分析:教师通过介绍这首名诗,使学生意识到数学思想无处不在。在这首诗中,随着帆船渐行渐远,帆船的影像越来越小,最终会无限趋近于0,消失在水天交界处。这一案例,能够培养学生的人文情怀和数学思想。
案例2:介绍定积分产生的历史背景,介绍我国古代数学家刘徽的“割圆术”。“割之弥细,所失弥少。割之又割,以至于不可割,则与圆周合体而无所失矣。”这是原始的积分思想。用“割圆术”求圆的面积以及周长和圆周率,这一发现比欧洲早一千多年。
案例3:我国隋代赵州桥的曲拱,是用一块块直棱石料巧妙构造的。这构思奇特的赵州桥不但在世界桥梁史上留下了光辉的一页,而且闪耀着高等数学启蒙思想的光芒,是微积分“以直代曲”思想的生动体现,也是微积分原理在建筑学上的朴素应用。
分析:这两个案例的介绍,既能使学生了解数学史,激发民族自尊心和自豪感,又能培养学生不怕困难、刻苦学习的精神。
2.曲边梯形面积的求法——难点的处理
如何计算由曲线y=x2和直线x=0、x=1、y=0围成的图形面积呢?教师可引导学生利用赵州桥的“以直代曲”原理来解决问题。
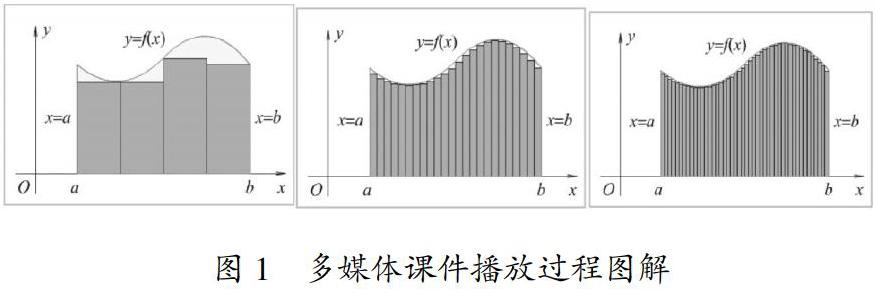
在直角坐标系上画出曲边梯形,由y=f(x)>0、x=a、x=b、x轴所围成说明x轴称为底边,曲线y=f(x)称为曲边。问题启动:面积等于多少?几何说明直边梯形的面积公式此时失效了,要求学生尝试模仿刘徽的“割圆术”、赵州桥的“以直代曲”原理来求曲边梯形面积,即由模仿到创新。创设情境如下:播放多媒体课件(见图1)并要求学生观察思考,在曲边梯形内摆满小矩形,当小矩形越来越多时,小矩形面积之和与曲边梯形面积之间的误差将如何变化?组织学生展开分组讨论,不难得到“随着矩形个数的增多,小矩形面积之和越来越接近于曲边梯形的面积。显然,分割得越细,近似程度越高,误差越小”。在学生讨论的过程中,教师要求学生思考:如果在分割的时候采取等分区间而不是任意分割区间是否可以呢?通过教师的引导,学生不难得出:因为推导论证过程要有严密性,所以不能以等分代替任意分割区间。这一过程,也是对学生的思维严谨性的训练。


在数学课程的学习中,高职学生的形象思维和小组合作能力毫不逊色本科学校的学生。教师通过“复习回顾、提出问题、创设情境、分组讨论、小组代表回答、教师总結归纳”这一师生互动过程来讲明本次课的教学难点——“曲边梯形面积的求法”,能使学生更易于接受。以上难点的处理,也是为了说明本次课的重点:“定积分的几何意义”的关键所在。教师通过模仿刘徽的“割圆术”、赵州桥的“以直代曲”原理来求曲边梯形面积,即由模仿到创新,提高了学生归纳规律、解决问题的能力。
3.定积分的定义——由归纳到演绎、由难点到重点的过渡


四、结语
总之,作为高职院校的数学教师,要充分认识到数学教学中融入思想政治教育的重要性,深入挖掘数学学科中的思想政治教育资源,不断将学生的思想政治教育工作渗透到自己日常的教学中。这样,既能有效地调动学生学习数学的积极性,又能真正做到“教书育人”,做学生成长成才道路上的“指明灯”。
参考文献:
[1]李辉.基于数学课堂教学的思想政治教育初探[J].中国电力教育,2013(07).
[2]马艳英,付彤,王青梅.将数学建模思想融入大学数学教学中的研究[J].吉林工程技术师范学院学报,2018(09).
[3]张国勇.高职数学课程改革的认识与思考[J].交通职业教育,2006(05).
[4]金晶晶.高职数学课程的思想政治教育功能研究[J].柳州职业技术学院学报,2015(01).

