一类弯曲空间超可积哈密顿系统的研究
闫梦姣,黄晴
(西北大学数学学院,陕西 西安 710127)
1 引言
根据刘维尔意义下完全可积性[1-2]的定义,一个自由度为n的哈密顿系统H若有包括在H内的n个相互独立且两两对合的守恒积分,那么系统H在刘维尔意义下就是完全可积的.此外,如果完全可积系统H还存在仅与H对合,未必与其他守恒积分对合且相互独立的m个守恒积分,则称系统H为超可积系统.m的最大值为n−1,当m=n−1时,系统H是最大超可积系统[3].对两个自由度的系统而言,最大超可积性与超可积性是等价的.有限维哈密顿系统的可积性和超可积性的相关研究已有很多成果,可参考综述性文献[4]及其中文献.这些成果大部分是基于常曲率空间或零曲率空间的,因为变曲率空间复杂多变,相关的分析和计算有很大难度.但变曲率空间却是更常见的空间,因此对于变曲率空间中有限维哈密顿系统的研究有很重要的意义.
变曲率空间中有限维哈密顿系统的研究也有一些结果,文献[5]分析了变曲率空间中一类二维哈密顿系统的超可积性.文献[6]不仅利用二次守恒积分得到了非常曲率空间中的n维最大超可积系统,还根据Bertrand理论得到了变曲率空间中一类新的超可积模型[7],随后又通过Stäckel变换得到了非常曲率空间中的四种最大超可积经典哈密顿系统[8].最近,文献[9]利用微分Galois理论研究了弯曲空间中形如
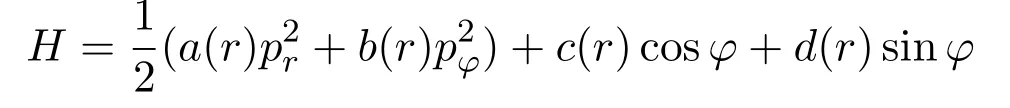
的哈密顿系统的可积必要条件,其中a(r),b(r),c(r),d(r)都是关于r的任意亚纯函数,还将得到的结论应用到三个具体的实例中来展示这些结论的简便实用性.
本文主要根据文献[9]中的第一个实例展开研究,分析形如
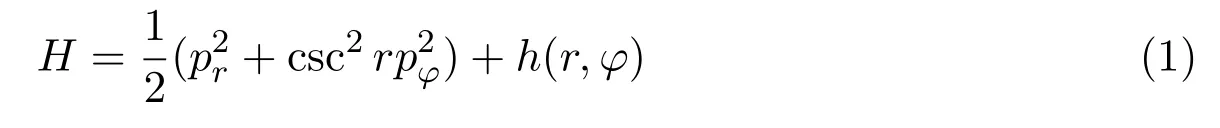
的哈密顿系统的可积性和超可积性.主要的分析方法是利用动能的Killing向量场构造系统的二次守恒积分,得到可积系统和超可积系统.最后,构造各个超可积系统中守恒积分的Poisson代数,并给出这些守恒积分之间的多项式代数关系.
2 哈密顿系统 (1)的可积性
哈密顿系统(1)的动能为:
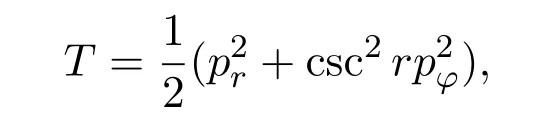
其Killing向量场由与T正交且关于动量pr和pφ线性的函数
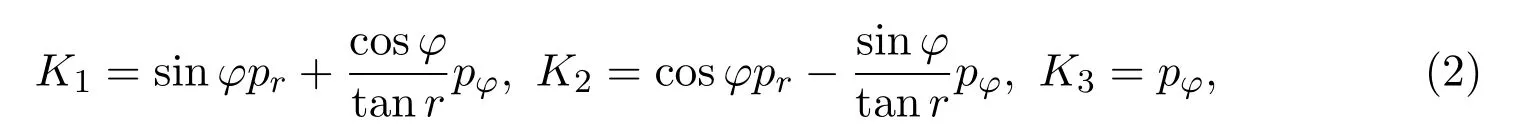
张成,其中三个Killing向量满足交换关系:
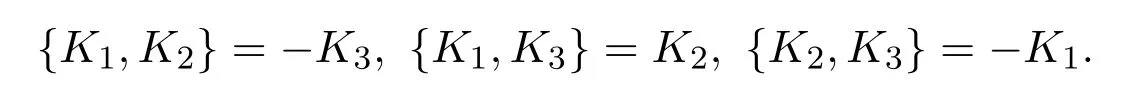
由此可知K1,K2,K3形成了一个SO(3)代数,它的一个Casimir函数为:
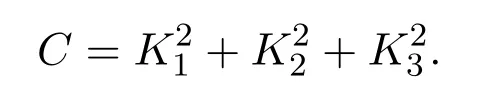
这个代数还容许以下变换:
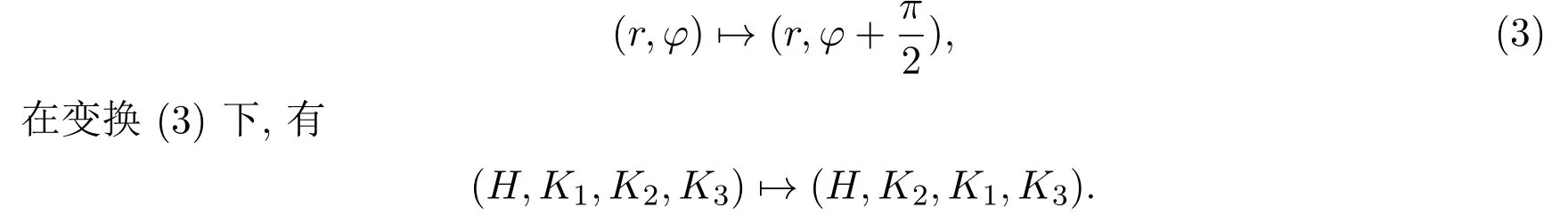
哈密顿系统二次守恒积分的一般形式为:
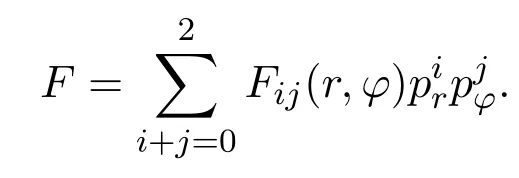
因为奇次和偶次不能同时出现[10],只需考虑:
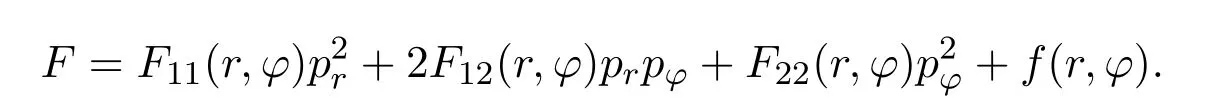
这里利用动能T的Killing向量场(2)构造守恒积分,仅考虑以下形式的二次守恒积分:
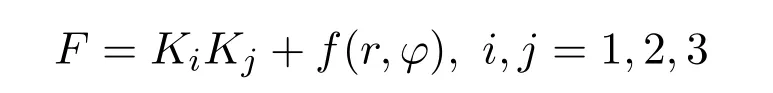
其中Ki,Kj为(2)中的Killing向量.若假设
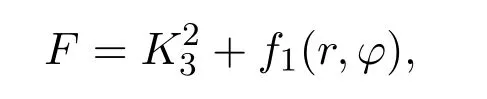
是系统(1)的守恒积分.根据Poisson交换关系{H,F1}=0,可解得h,f1为:
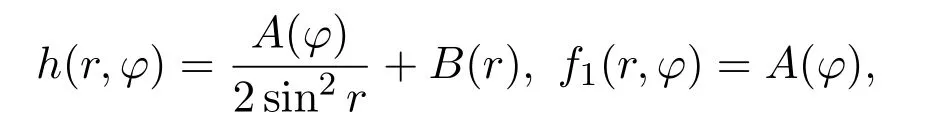
其中A(φ),B(r)分别是关于r,φ的任意函数.经检验H,F1相互泛函独立,所以系统
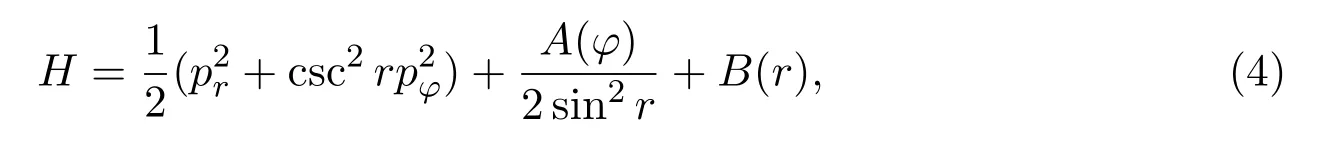
是刘维尔完全可积的.
3 哈密顿系统 (4)的超可积性
完全可积系统(4)如果还存在另一个守恒积分F2,且H,F1,F2相互独立,则(4)是超可积的.本节通过引入新的二次守恒积分讨论(4)的超可积性,以建立超可积系统和相应的Poisson代数.
3.1 超可积约束 F2=K1K3+f2(r,φ)
假设系统(4)容许如下形式的二次守恒积分:
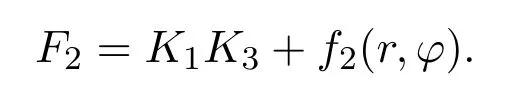
根据{H,F2}=0得到pr,pφ的系数,并令这些系数等于零得到A,B,f2满足:
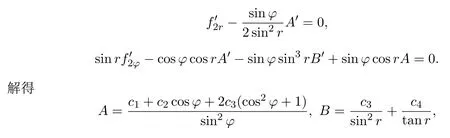
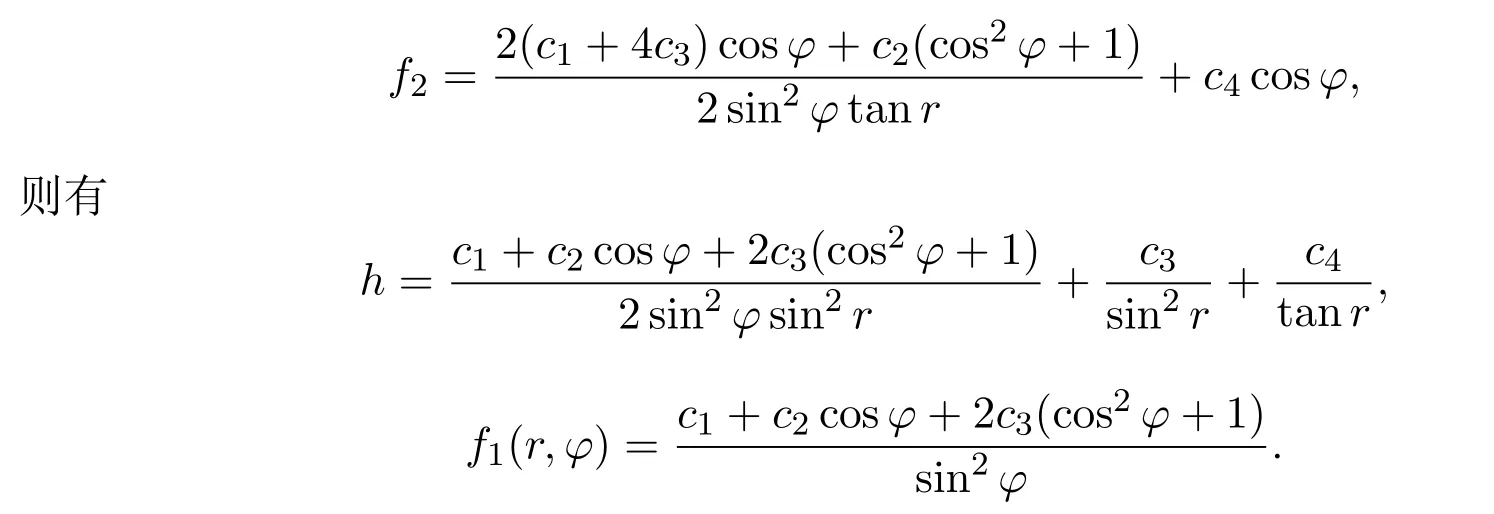
易知,H,F1,F2相互独立,可得到超可积的哈密顿系统.由于F1和F2的交换子不能用H,F1,F2来表示,为构造守恒积分的Poisson代数,引入
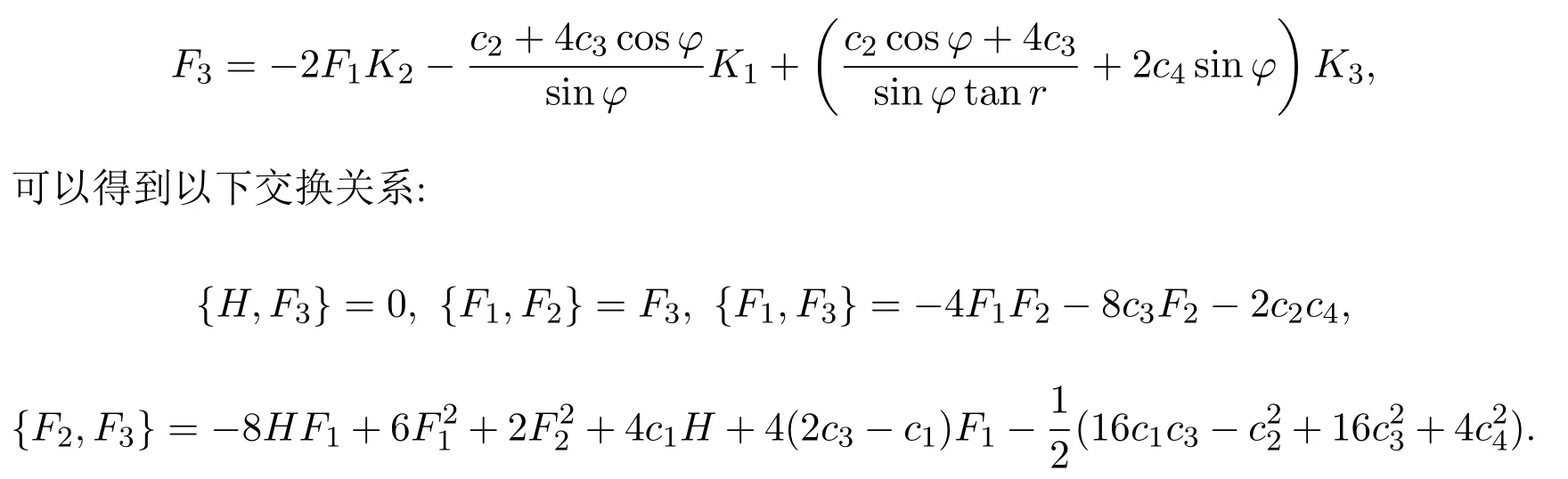
因此H,F1,F2,F3构成一个Poisson代数.二维可积哈密顿系统最多有3个相互独立的守恒积分,故H,F1,F2,F3应是相互依赖的,这四个守恒积分所满足的多项式代数关系为:
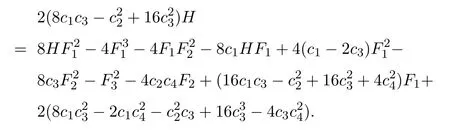
此外,对以上所得超可积系统实行变换(3),还能得到如下超可积系统:
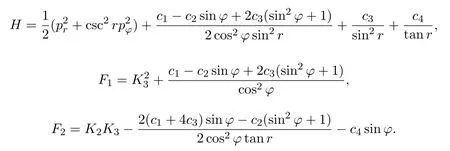
3.2 超可积约束 F2=K22+f2(r,φ)
假设系统(4)有如下形式的二次守恒积分:
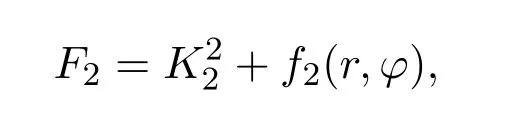
由{H,F2}=0,得到A,B,f2所满足的方程组,解得
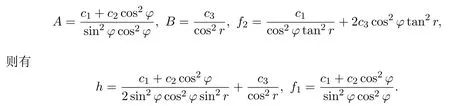
为构造封闭的Poisson代数,引入如下函数:
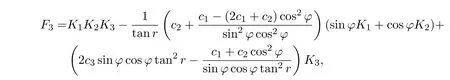
则H,F1,F2,F3满足以下非零交换关系:

由此守恒积分H,F1,F2,F3构成一个Poisson代数,其中各积分满足以下关系:
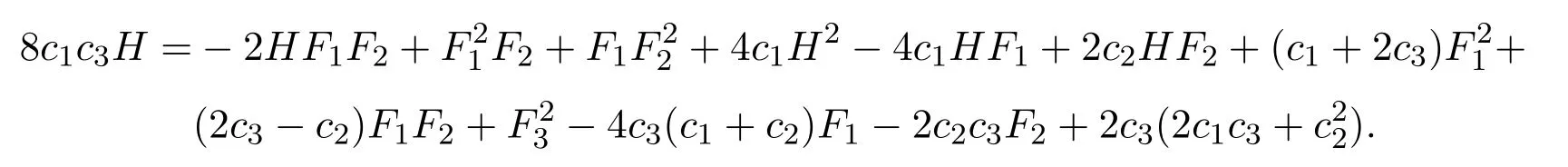
对该系统做变换(3)可得如下超可积系统:
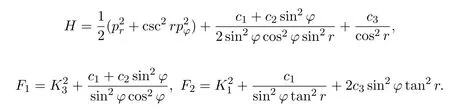
3.3 超可积约束 F2=K1K2+f2(r,φ)
如果系统(4)容许形如
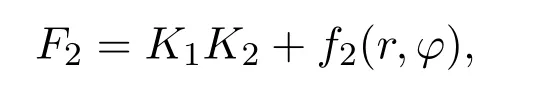
的二次守恒积分,由{H,F2}=0解得
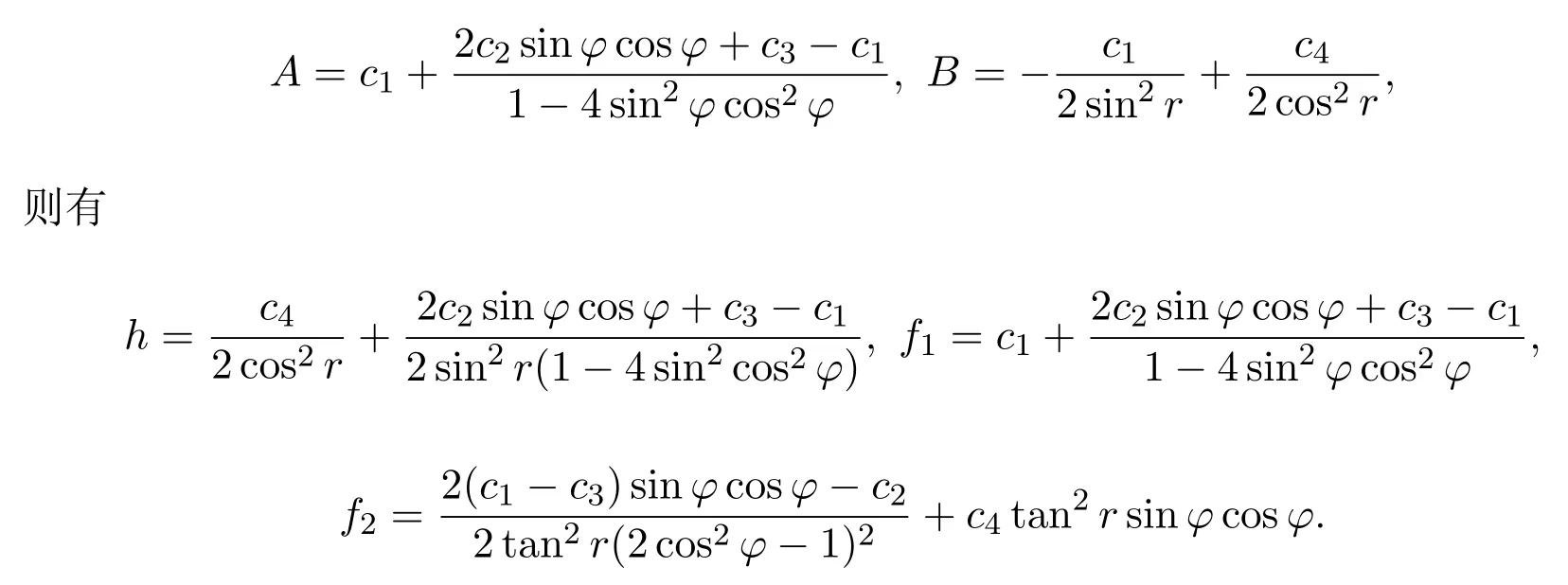
经检验H,F1,F2不满足封闭的Poisson代数关系,令
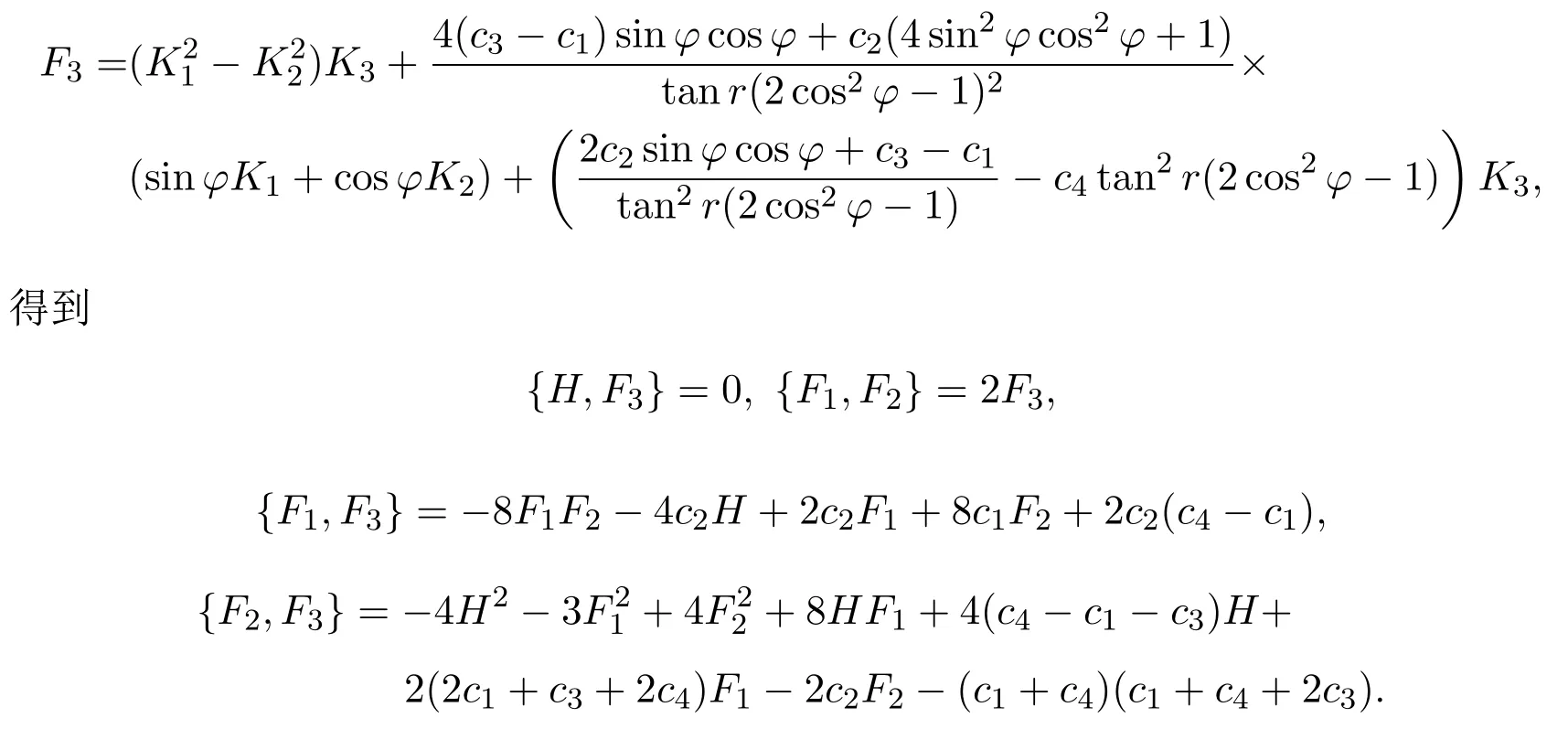
H,F1,F2,F3构成一个Poisson代数且满足:
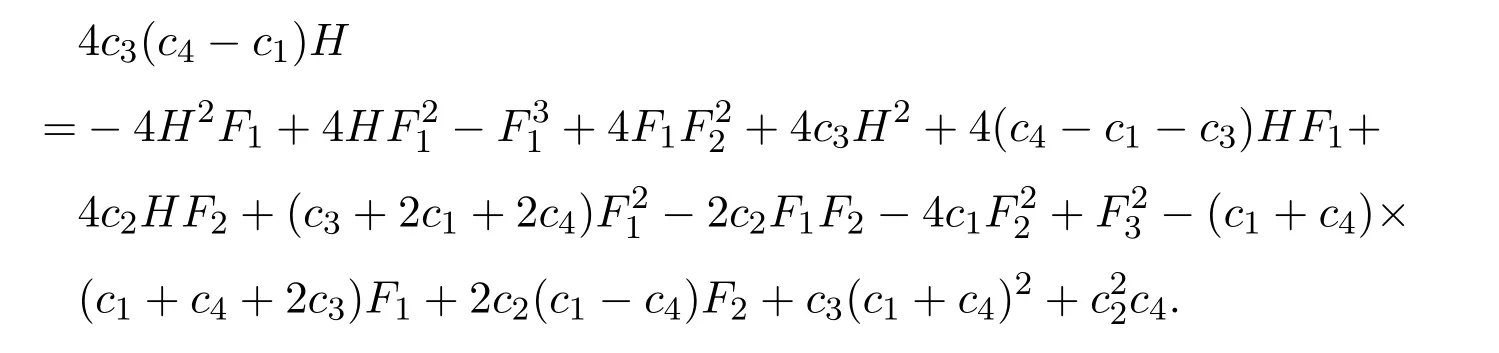
4 总结
本文利用动能的Killing向量场构造二次守恒积分,得到了一系列弯曲空间的2维超可积系统,并对每个超可积系统给出了相应的守恒积分构成的Poisson代数以及Poisson代数中各守恒积分之间的代数关系.

