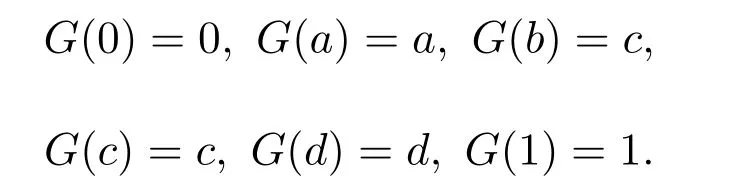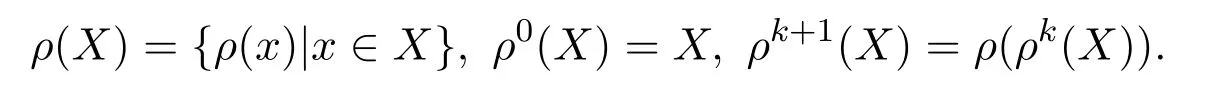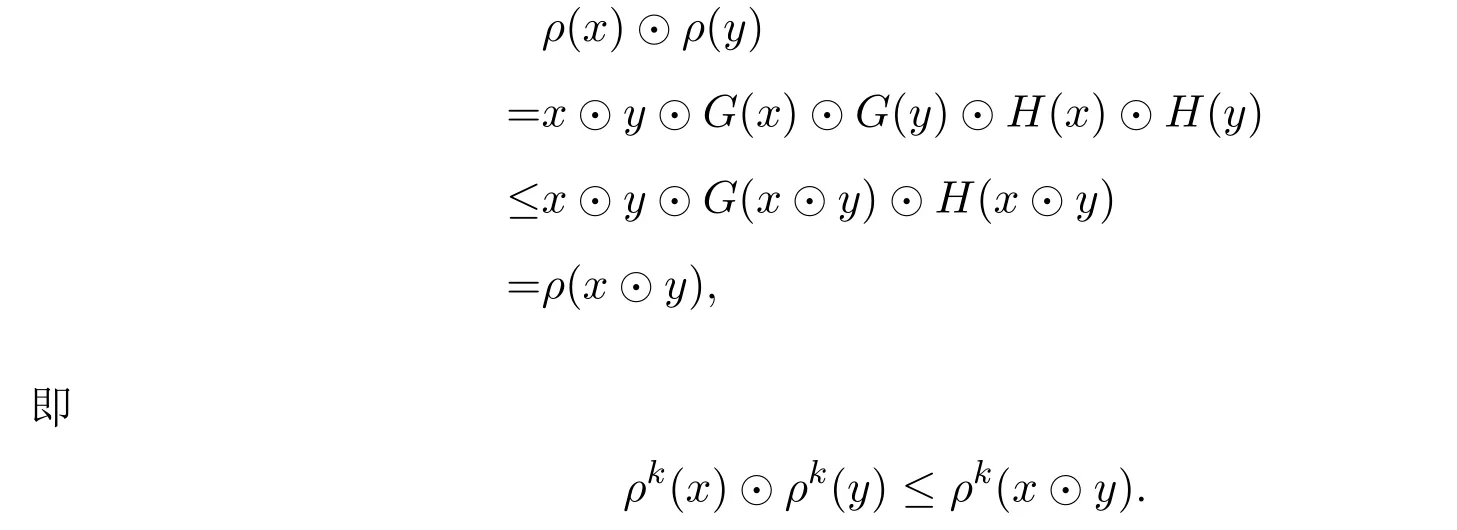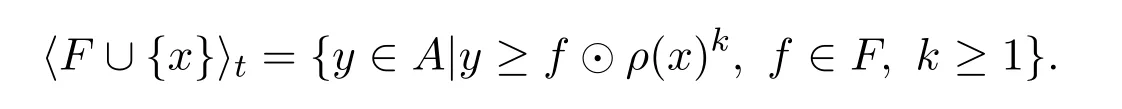有界半Hoops上的时态算子
牛海灵,辛小龙
(西北大学数学学院,陕西 西安 710069)
1 引言
Hoops代数是自然序的交换剩余整幺半群,由文献[1-2]引入.半Hoops是Hoops的一般化,它最初由文献[3]引入,被称为互补半群.半Hoops[4]是最基本的剩余结构,而且包含所有基于剩余格的逻辑代数.它与剩余格[5]比较,半Hoops是交半格,不满足并半格;与Hoops代数比较,半Hoops是不满足可分性.
对于命题逻辑,经典和非经典逻辑都不包含时间维度,为了获得时态逻辑,文献[6]用新的一元算子来丰富给定的命题逻辑,用G,H,F,P表示,通常把这些算子叫做时态算子.时态算子F和P通过G和H来表示:
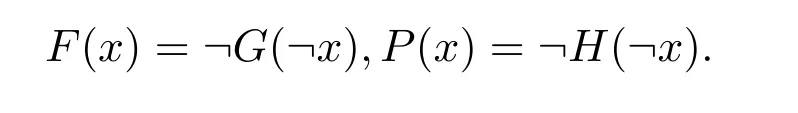
文献[6]首次引入时态算子在经典逻辑中,随后,在非经典逻辑中引入时态算子.比如说,Hetying代数,Basic代数和Effect代数上的时态算子[7-9].近年来,越来越多的学者不断地在不同逻辑代数中研究时态算子,如:模糊逻辑,MV-代数上,伪MV-代数上,不可交换剩余格上的时态算子[10-13]等.
基于以上内容,拓展了时态算子在更广泛的非经典逻辑代数中,即半Hoops.给出了半Hoops上的时态算子及研究其性质,给出了时态滤子的定义,刻画了时态滤子.探究了极大时态滤子,得到了一些重要结果.
2 预备知识
定义 2.1[4]一个(2,2,2,0)型的代数A=(A,⊙,→,∧,1)若满足下列条件:
(1)(A,∧,1)是一个有最大元1的交半格;
(2)(A,⊙,1)是一个可换半群;
(3)(x⊙y)→z=x→(y→z),对任意的x,y,z∈A.
则称 (A,⊙,→,∧,1)为半 Hoops代数.
在一个半 Hoops代数 (A,⊙,→,∧,1)上,定义对任意的x,y∈A,x≤y当且仅当x→y=1.易验证≤是A上的偏序关系,对任意的x∈A,x≤1.
对任意的x∈A,定义x0=1且xn=xn−1⊙x对任意的n∈N.
命题 2.1[4]设 (A,⊙,→,∧,1)是一个半 Hoops代数.则下面性质成立:对任意的x,y,z∈A,
(1)x⊙y≤z当且仅当x≤y→z;
(2)x⊙y≤x,y;
(3)1→x=x,x→1=1;
(4)xn≤x;
(5)y≤x→y;
(6)若x≤y,则y→z≤x→z,z→x≤z→y且x⊙z≤y⊙z;
(7)x→y≤(z→x)→(z→y),x→y≤(y→z)→(x→z);
(8)y⊙(y→x)≤x.
一个半Hoops(A,⊙,→,∧,1)称为有界半Hoops,若存在一个元素0∈A使得对任意的x∈A有0≤x.
在一个有界半Hoops代数(A,⊙,→,∧,0,1)中,对任意的x∈A,通过¬x=x→0定义运算“¬”.若对任意的x∈A有¬¬x=x,则称这个有界半Hoops(A,⊙,→,∧,0,1)具有双重否定性,简称为DNP条件.
为了方便,记有界半 Hoops代数 (A,⊙,→,∧,0,1)为A.
命题2.2[14]设A是一个有界半Hoops代数.则下面性质成立:对任意的x,y∈A,
(1)¬1=0,¬0=1;(2)x≤¬¬x;(3)¬x=¬¬¬x;
(4)若x≤y,则¬y≤¬x;(5)x→y≤¬y→¬x;
(6)¬x→y≤¬y→x.
命题 2.3[14]设A是一个有界半Hoops代数.对任意的x,y∈A,定义
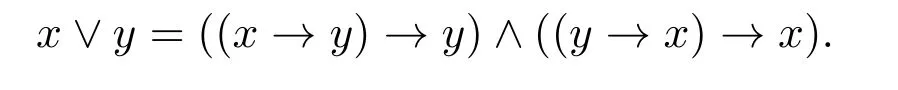
则以下条件等价:对任意的x,y,z∈A,
(1)∨在A是可交换的;
(2)若x≤y,则-x∨z≤y∨z;
(3)x∨(y∧z)≤(x∨y)∧(x∨z);
(4)∨是A上的并运算.
命题 2.4[14]一个半Hoops称为是∨−半Hoops,若它满足命题2.3中的其中一个条件.
命题 2.5设A是一个有界∨−半Hoops代数.则下面性质成立:对∀x,y∈A,
(1)¬(y∧z)≥¬y∨¬z;
(2)(x∧y)⊙z≤(x⊙z)∧(y⊙z).
3 有界半 Hoops上的时态算子
定义3.1设A是一个有界半Hoops代数且G,H:A→A是一元算子.(A,G,H)称为时态半Hoops,(G,H)称为时态算子,若满足下列条件,对任意的x,y∈A,
(A1)G(1)=H(1)=1;
(A2)G(x→y)≤G(x)→G(y),H(x→y)≤H(x)→H(y);
(A3)x≤GP(x),x≤HF(x),其中P(x)=¬H(¬x),F(x)=¬G(¬x).
例 3.1设A={0,a,b,1}且0 则A是一个半Hoops[14].在A上定义算子G和H如下: 经过验证可知,G和H是A上的时态算子. 命题3.1设(A;G,H)是一个时态半Hoops,则下面性质成立:对任意的x,y∈A, (1)F(0)=P(0)=0; (2)若x≤y,则O(x)≤O(y),其中O∈{G,H,F,P}; (3)G(x)⊙G(y)≤G(x⊙y),H(x)⊙H(y)≤H(x⊙y); (4)对于A的任意一族元素{xi}i∈I,有G(∧xi)≤ ∧G(xi)和H(∧xi)≤ ∧H(xi); (5)PG(x)≤¬¬x,FH(x)≤¬¬x,特别地,PG(¬x)≤¬x,FH(¬x)≤¬x; (6)G(x→y)≤F(x)→F(y),H(x→y)≤P(x)→P(y); (7) (8)P≤PGP,F≤FHF. 证明(1)由F(x)和P(x)的定义可知,(1)成立. (2)由(A2)可知,当x≤y时,有G(x)≤G(y).若x≤y,则¬y≤¬x.由算子G的单调性可知,有G(¬y)≤G(¬x),进而¬G(¬x)≤¬G(¬y).因此F(x)≤F(y). 其余证明类似. (3)由A(2)可知,G(x→y)⊙G(x)≤G(y).令y=y⊙x,得到 算子H的证明类似. (4)对任意的j∈I,因为∧xi≤xj,则G(∧xi)≤G(xj),进而G(∧xi)≤ ∧G(xi). 算子H的证明类似. (5)由A(3),得出对任意的x∈A,x≤HF(x).所以¬x≤HF(¬x). 因为x≤¬¬x,则¬G(¬¬x)≤¬G(x).因此 特别地,因为¬x=¬¬¬x,所以PG(¬x)≤ ¬x. 其余证明类似. 另一个不等式证明类似. (8)由A(3)可知,x≤GP(x).又由(2),则P(x)≤PGP(x). 另一个不等式证明类似 命题 3.2设(A;G,H)是一个时态半Hoops且满足DNP条件,则下面性质成立:对任意的x,y∈A, (1)PG(x)≤x,FH(x)≤x; (2)P=PGP,F=FHF; (3)对于A的任意一族元素{xi},有G(∧xi)=∧G(xi)和H(∧xi)=∧H(xi). 证明(1)由命题3.1(5)和x=¬¬x可知,(1)成立. (2)由命题3.1(8)和命题3.2(1)可知,(2)成立. (3)设对任意的i∈I,y≤G(xi).由命题3.1(2)可知,P(y)≤PG(xi)≤xi,所以P(y)≤∧xi,进而y≤GP(y)≤G(∧xi).另一方面,由3.1(4)可得.因此(3)成立. 一个框架是一个序对(X,R),其中X是非空集合,R是X上的二元运算.集合X被认为是时间尺度,关系xRy表示 “x在y之前”和 “y在x之后”.假设A是一个半Hoops且X是一个集合.则AX是X到A的全部映射的集合,满足运算: 验证AX是半Hoops. 命题 3.3设{xi|i∈I}和{yi|i∈I}是A的任意族元素.则 证明由命题2.5(2),对任意的i∈I, 因为对任意的i∈I,(xi→yi)⊙xi≤yi,所以 定理 3.1设A是一个∨-半Hoops且(X,R)是一个框.定义算子G∗和H∗是AX到自身的映射,其中对任意的f∈AX和x∈X, 则 (AX;G∗;H∗)是一个时态半Hoops. 证明(1)对任意的y∈X,f(y)=1,所以G∗(f)=f.因此G∗(1)=H∗(1)=1. (2)对于f,g∈AX和x∈X,利用命题2.5(2)和命题3.3可得, 定义 4.1有界半HoopsA中的一个滤子F称为时态滤子,若对任意的x∈F,则G(x),H(x)∈F. 例 4.1设A={0,a,b,c,d,1}且0 则A是一个半Hoops[14],其中对任意的x,y∈A,x∧y=x⊙(x→y).在A上定义算子G=H如下: 反复验证可知G和H是A上的时态算子,且F={1,a}是时态滤子. 记全体滤子为Ft(A). 注 4.1设A是一个有界半Hoops且F是A的一个时态滤子.F是一个真滤子当且仅当0. 定义 4.2设 (A;G,H)是时态半Hoops.定义A上的运算ρ如下:对任意的x∈A,ρ(x)=x⊙G(x)⊙H(x). 易验证A中的滤子是时态滤子当且仅当它关于运算ρ封闭. 对任意的n≥1,定义ρ0(x)=x,ρn+1(x)=ρ(ρn(x)).同时,对A中的任意非空子集X,定义ρk(X)如下: 命题 4.1设(A;G,H)是时态半Hoops.则对任意的x,y∈A和n,k≥1,下列性质成立: (1)ρn(0)=0,ρn(1)=1,ρn+1(x)≤ρn(x); (2)若x≤y,则ρn(x)≤ρn(y); (3)ρk(x)⊙ρk(y)≤ρk(x⊙y). 证明(1)和(2)是显然的. (3)由命题3.1(3)可知, 设A是半Hoops且X是A的非空子集.则X生成的时态滤子是指包含X的最小时态滤子,记为. 推论 4.1设F是A的时态滤子且x∈A.则 证明证明类似于定理4.1. 定义4.3设A是半Hoops且M是A的真时态滤子.M称为A的极大时态滤子,若它没有真包含在A的任何其它真时态滤子中.记A中的所有时态滤子的集合为M(A). 命题 4.2设A是半Hoops且M是A的真时态滤子.则下列条件等价: (1)M∈M(A); (2)若,则 证明(1)⇒(2)若,则M⊆因为M∈M(A),所以 (2)⇒(1)设G是A的真时态滤子使得M⊆G且MG,则存在x∈G使得.由(2)可知,因为所以A=G,这与G⊆A中矛盾.因此M∈M(A). 命题 4.3设A是半Hoops且M是A的真时态滤子.则下列条件等价: (1)M是极大时态滤子; (2)对任意的x∈AM,存在f∈M和n∈N使得f⊙ρ(x)n=0. 证明(1)⇒(2)设M是A的极大时态滤子.若x∈AM.由命题4.2可知,由推论 4.1和 0∈A可得 0≥f⊙ρ(x)n.因此f⊙ρ(x)n=0. (2)⇒(1)设G是A的真时态滤子使得M⊆G.则存在x∈G使得.由 (2),存在f∈M和n∈N使得f⊙ρ(x)n=0,所以 0∈G,从而G=A.因此,M是极大时态滤子. 定理4.2设A是有界半Hoops且M是A的真时态滤子.若M是A的极大时态滤子.则对任意的当且仅当存在n∈N使得¬ρ(x)n∈M. 证明(1)⇒(2)设M是极大时态滤子且x∈A.若,由命题4.3可得,存在f∈M和n∈N,使得f⊙ρ(x)n=0,所以f≤ρ(x)n→0=¬ρ(x)n.因为M是滤子,所以¬ρ(x)n∈M. (2)⇒(1)设x∈A且存在n∈N使得¬ρ(x)n∈M.假设x∈M.因为M是时态滤子,则对任意的n∈N,使得ρ(x)n∈M,从而 0=¬ρ(x)n⊙ρ(x)n∈M,这与M是真滤子矛盾.因此对任意的.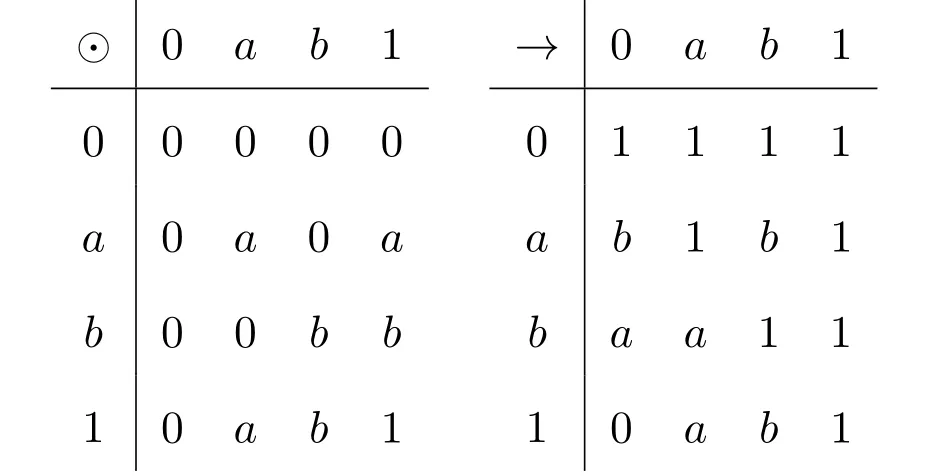

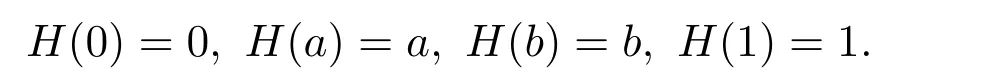
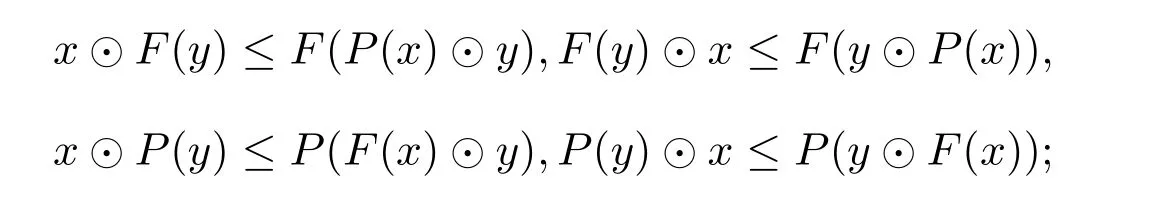
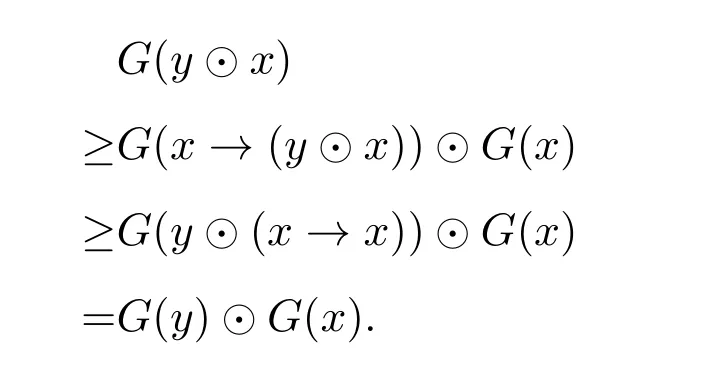
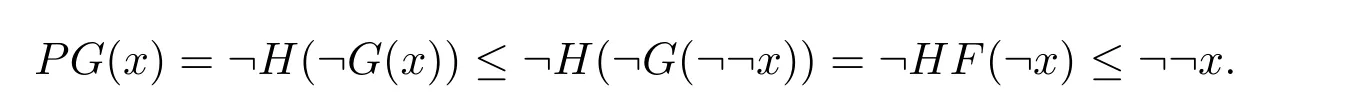

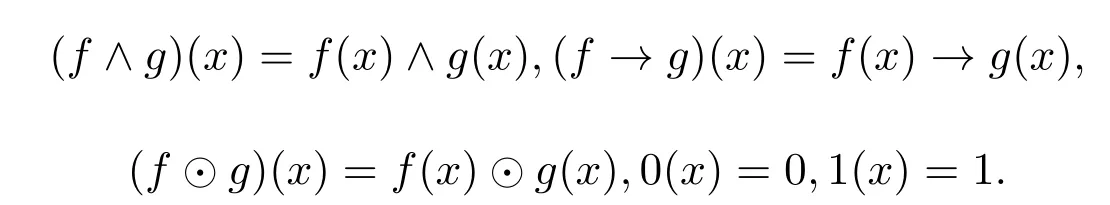
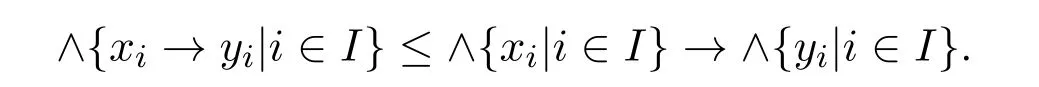
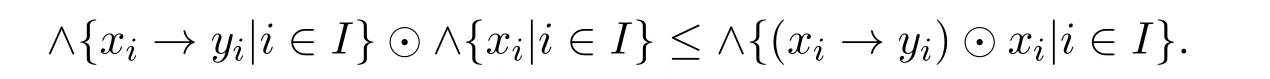
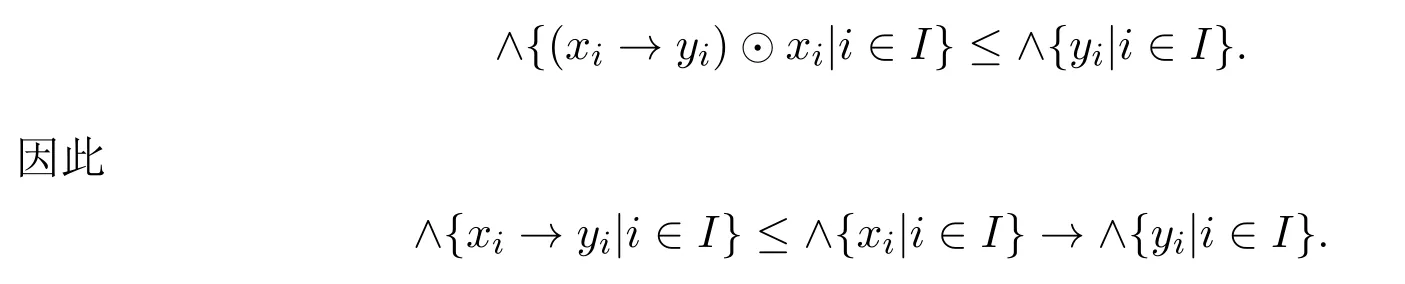
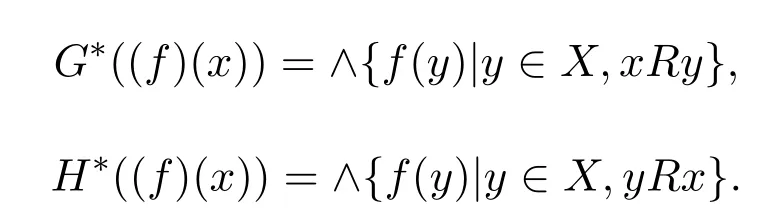

4 有界半 Hoops上的时态滤子