无人机多光谱遥感监测冬小麦拔节期根域土壤含水率

杨珺博，王 斌，黄嘉亮，张智韬,2，周永财,2，姜文焕

(1.西北农林科技大学水利与建筑工程学院，陕西 杨凌 712100；2.西北农林科技大学 旱区农业水土工程教育部重点实验室，陕西 杨凌 712100)

0 引 言

准确获取土壤水分数据是实现作物增收的关键因素，对农业生产中的水资源高效利用具有重要意义[1-3]。遥感监测土壤含水率具有高效、准确等优点，已成为国内外研究重点，但卫星遥感易受天气等因素影响，而且不能同时满足农田尺度的高时空分辨率要求[4-6]。无人机遥感监测土壤含水率具有时效性快、成本低、机动灵活等优点[7,8]，可以迅速准确地完成特定区域内的农情监测任务[9,10]。

近年来，国内外学者在无人机遥感监测土壤含水率方面已经取得了许多研究成果。Li[11]等利用无人机多光谱系统获取棉花冠层光谱数据，发现红、近红外波段反射率与土壤水分有较好的相关性。HASSAN-ESFAHANI[12]等借助于人工神经网络算法(Artificial Neural Network，ANN)，通过无人机多光谱遥感数据构建了表层土壤含水率监测模型。王海峰等[13]基于获取的多光谱遥感数据，利用相关系数法筛选对土壤水分较敏感的波段，通过单一敏感波段处的光谱数据建立不同的一元回归模型，实现对裸土土壤含水率高精度监测。Oliver[14]等采用无人机遥感数据计算的温度植被干旱指数(Temperature Vegetation Dryness Index，TVDI)和归一化植被指数(Normalized difference vegetation index，NDVI)反演地表5～10 cm土壤含水率，模型监测精度较高。陈硕博等[15]以抽穗期冬小麦为研究对象，利用无人机搭载多光谱相机来获取作物冠层光谱数据，提出一种差值反射率(DR)实现对土壤水分较高精度的反演。虽然这些研究取得了较好的效果，但主要集中在无人机多光谱遥感对土壤表层含水率的反演，对于植被覆盖条件下，无人机多光谱遥感对不同深度土壤含水率反演精度的研究较少。

本文以陕西省杨凌区拔节期冬小麦为研究对象，利用无人机搭载六波段多光谱相机获取冬小麦冠层反射率信息，建立各波段特征值与不同深度土壤含水率之间的多元回归模型，探究作物根域土壤含水率的最优监测模型以及最佳监测深度，以期为无人机多光谱遥感反演植被覆盖条件下不同深度的田间土壤含水率提供参考。

1 材料与方法

1.1 研究区概况

本试验在陕西杨凌西北农林科技大学旱区农业水土工程教育部重点实验室的灌溉试验站( 34°17'N，108°04'E，海拔521 m)的试验田(如图1)进行，该地区地处暖温带，属大陆性季风气候，年平均气温在12 ℃左右，多年平均降雨量为630 mm，年均蒸发量884 mm，土壤干容重1.38 g/cm3。

图1 试验小区布置图Fig1. Test plot layout

1.2 试验材料与设计

本试验冬小麦品种选用小偃22，于2018年10月15日人工播种，试验田共播种7.68 kg种子(每袋小麦称重40 g)，并且施用了20 kg的复合肥料作为底肥。小麦在生长过程中严格控制水量，本次试验的12个小区，每个小区面积为4×4=16 m2，小区内种植的冬小麦行距25 cm，每行播种量为40 g。共设置4种不同的控水处理(I、II、III、IIII)：0.95田持、0.8田持、0.65田持、0.5田持，每种控水处理设置3个重复，为减少外界环境的干扰，各小区都配有遮雨棚。

1.3 数据采集

1.3.1 土壤水分数据获取

利用土钻采集10、20、30、40、60 cm深度的土样，每个深度取30 g左右的土壤并将其放入铝盒，采用烘干法测定土壤质量含水率，其计算式为：

(1)

式中：W1为湿土加铝盒质量；W2为干土加铝盒质量；W3为空铝盒质量。

1.3.2 无人机平台与冠层数据获取

本试验采用深圳市大疆创新科技有限公司生产的MATRICE 600型六旋翼无人机，搭载美国Tetracam 公司生产的Micro-MCA 型多光谱相机(每个波段配备1. 3M像素CMOS传感器，每张图像分辨率为1 280×1 024 像素) ，如图2所示，该相机有6个镜头，分别对应6个波段，波长分别为490 nm(蓝光)、550 nm(绿光)、680 nm(红光)、720 nm(红边)、800 nm(近红外)、900 nm(近红外)。无人机遥感影像获取时间为2019 年3月26-28日，获取时刻为下午13∶00左右，天气晴朗无风，视野良好。此时的冬小麦生长正处于拔节期，生长旺盛。无人机飞行高度为15 m，镜头垂直向下，获取遥感影像前，在试验区域内布置标准白板和黑板进行辐射标定，从而获取小麦冠层光谱反射率。

图2 无人机及机载传感器Fig.2 Unmanned aerial vehicle and airborne sensor

1.4 数据处理

采用多光谱相机自带的处理软件Pixel Wrench2对3d内获取的遥感图像进行预处理。将处理后的图像导入实景三维建模软件Agisoft PhotoScan Professional (64 bit)中进行遥感图像的拼接处理。将拼接完成的.tif格式图像导入ENVI 5.3(64bit)软件中，利用监督分类法剔除土壤背景的影响并提取出该时间点各小区冬小麦冠层6个波段的反射率。数据分析借助于IBM SPSS Statistics 23.0、DPS7.05。

1.5 精度评价

建模集精度检验利用回归分析得到的模型决定系数R2、显著性差异水平F、检验水平P，当R2越接近于1，显著性F越大，检验水平p越接近于0时说明回归方程拟合程度越高。

验证集的预测效果通过模型决定系数R2、均方根误差RMSE和相对分析误差RPD三个指标来评价。验证R2越大，均方根误差RMSE越小，相对分析误差RPD越大，表明模型的反演效果越好[16]。计算公式如下：

(2)

(3)

(4)

2 结果与分析

2.1 各波段反射率与不同深度土壤含水率相关性分析

计算各波段反射率与不同深度土壤含水率的相关系数，结果如表1所示。由表1可知，各波段反射率对不同深度的土壤含水率敏感程度不同，波段1～4与10、20 cm的土壤含水率皆有较好的相关性，相关系数都达到了0.6以上。10、20 cm土壤含水率的最敏感波段均为波段3，相关系数r分别为-0.784，-0.724。对30、40、60 cm土壤含水率最敏感的是波段4，相关系数r都达到了0.4以上。波段5、波段6与各深度的土壤含水率相关性都较低。随着监测深度的加深，各波段对土壤含水率的敏感性都有不同程度的降低，光谱反射率与10、20 cm浅层土壤含水率的相关系数明显大于30、40、60 cm深层，当深度达到30 cm时相关系数皆有显著折减。

表1 光谱反射率与各深度土壤含水率相关系数表

Tab.1 Spectral reflectance and matrix of soilwater correlation coefficients at various depths

土壤深度/cm波段1波段2波段3波段4波段5波段610-0.772-0.593-0.784-0.628-0.430-0.46520-0.675-0.574-0.724-0.664-0.382-0.39930-0.268-0.348-0.391-0.497-0.161-0.12740-0.166-0.322-0.286-0.416-0.177-0.14460-0.063-0.392-0.276-0.4580.2600.240

2.2 回归模型

本试验连续进行3 d，采集样本数据共36个，随机选取其中2/3样本(n=24)作为建模集，剩下的1/3样本(n=12)用于验证。由于各波段反射率直接反演土壤含水率时可能会出现多重共线性问题[17]，故本文采用逐步回归法、偏最小二乘法、岭回归法进行多元回归分析，建模结果如表2所示。

由表2可以得出，3种建模方法在进行多元分析中表现出明显不同的统计性差异，逐步回归法在各个深度的模型拟合度R2都为最高，偏最小二乘法次之，岭回归法为三者最低。各模型决定系数R2与土壤含水率监测深度的变化关系如图3所示，对比分析可知浅层(10、20 cm)土壤含水率的模型拟合度明显高于深层(30、40、60 cm)，其中逐步回归法、偏最小二乘法、岭回归法在10 cm处的建模拟合度R2最高，分别为0.815、0.772、0.669，在20 cm深度的模型决定系数R2虽有一定下降，但逐步回归法和偏最小二乘法仍有较强的相关性(R2>0.7)，岭回归的拟合度R2为0.586。三种模型在10、20 cm建立的回归模型均具有统计学意义(P<0.01)。当深度达到30 cm时，三种模型的拟合度都有明显的折减，逐步回归法和偏最小二乘法的显著性也有不同程度的下降，其中岭回归模型在30、40、60 cm的回归模型检验水平P值皆大于0.1，且高于其余两种方法，这种突变的原因应是岭回归自身建模方式所造成的[18-20]，表明在此深度的土壤含水率监测模型无统计学意义。因此，无人机多光谱遥感对植被覆盖条件下的较深层(h>30 cm)土壤含水率难以进行有效监测，但对于作物根域浅层(0～20 cm)土壤含水率的反演具有很高可行性。

2.3 模型验证

为检验模型预测效果，将12组验证数据分别带入各回归方程中。通过实测值和预测值计算3种模型的决定系数R2、均方根误差RMSE和相对分析误差RPD，计算结果如表3，预测模型决定系数R2随土壤深度的变化关系见图4。

表2 基于不同波段反射率的各深度土壤含水率多元回归模型

Tab.2 Multiple regression models of soil moisture content at various depths based on reflectance at different bands

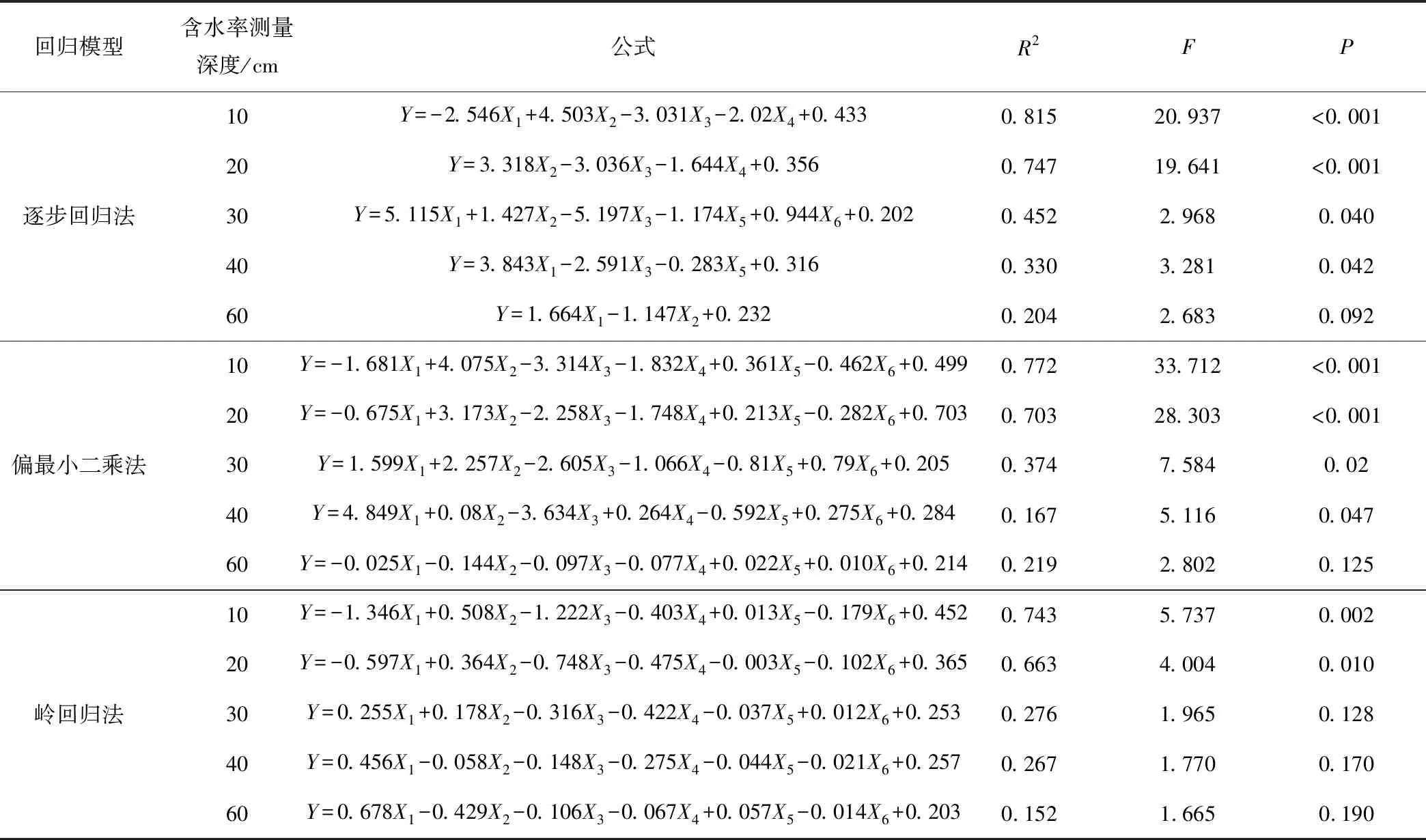
回归模型含水率测量深度/cm公式R2FP逐步回归法10Y=-2.546X1+4.503X2-3.031X3-2.02X4+0.4330.81520.937<0.00120Y=3.318X2-3.036X3-1.644X4+0.3560.74719.641<0.00130Y=5.115X1+1.427X2-5.197X3-1.174X5+0.944X6+0.2020.4522.9680.04040Y=3.843X1-2.591X3-0.283X5+0.3160.3303.2810.04260 Y=1.664X1-1.147X2+0.2320.2042.6830.092偏最小二乘法10Y=-1.681X1+4.075X2-3.314X3-1.832X4+0.361X5-0.462X6+0.4990.77233.712<0.00120Y=-0.675X1+3.173X2-2.258X3-1.748X4+0.213X5-0.282X6+0.7030.70328.303<0.00130Y=1.599X1+2.257X2-2.605X3-1.066X4-0.81X5+0.79X6+0.2050.3747.5840.0240Y=4.849X1+0.08X2-3.634X3+0.264X4-0.592X5+0.275X6+0.2840.1675.1160.04760 Y=-0.025X1-0.144X2-0.097X3-0.077X4+0.022X5+0.010X6+0.2140.2192.8020.125岭回归法10Y=-1.346X1+0.508X2-1.222X3-0.403X4+0.013X5-0.179X6+0.4520.7435.7370.00220Y=-0.597X1+0.364X2-0.748X3-0.475X4-0.003X5-0.102X6+0.3650.6634.0040.01030Y=0.255X1+0.178X2-0.316X3-0.422X4-0.037X5+0.012X6+0.2530.2761.9650.12840Y=0.456X1-0.058X2-0.148X3-0.275X4-0.044X5-0.021X6+0.2570.2671.7700.17060 Y=0.678X1-0.429X2-0.106X3-0.067X4+0.057X5-0.014X6+0.2030.1521.6650.190

注:Y为土壤质量含水率;X1为波段1反射率;X2为波段2反射率;X3为波段3反射率;X4为波段4反射率;X5为波段5反射率;X6为波段6反射率。

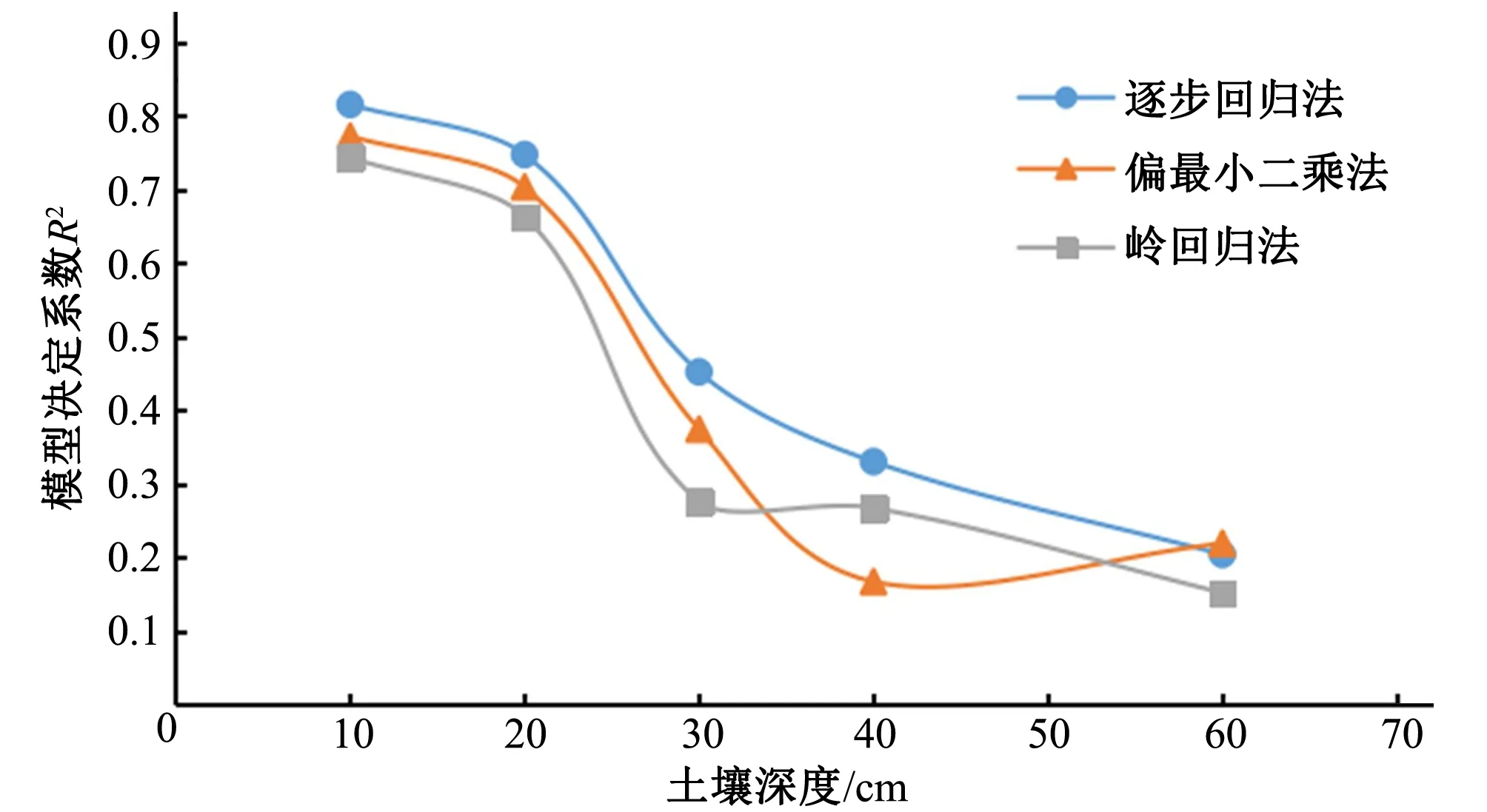
图3 各回归模型决定系数与土壤深度变化关系图Fig.3 Relationship between coefficient of determination and soil depth variation of each regression model

由表3可知，逐步回归法在10、20 cm的土壤含水率预测模型的决定系数R2达到了0.774、0.717，为三种方法中最高，相对分析误差RPD在10 cm处为2.007，表明模型在该深度时具有很好的定量预测能力(RPD>2)，深度达到20 cm时RPD值有略微下降，但也有较好的预测能力(RPD>1.8)。偏最小二乘法在10、20 cm的模型拟合度R2为0.771、0.709，略低于逐步回归法，其RPD值分别为1.938、1.836，都有较好的预测能力(RPD>1.8)。而岭回归法在10、20 cm处的R2(0.632、0.562)为三者最低，定量预测能力也低于前两者(RPD>1.4)。3种方法在各个深度的模型RMSE值均在允许范围内(0.1以下)。

表3 不同建模方法下土壤含水率的模型评价指标表

Tab.3 Comparison of predicted and measured values ofsoil moisture content under different modeling methods

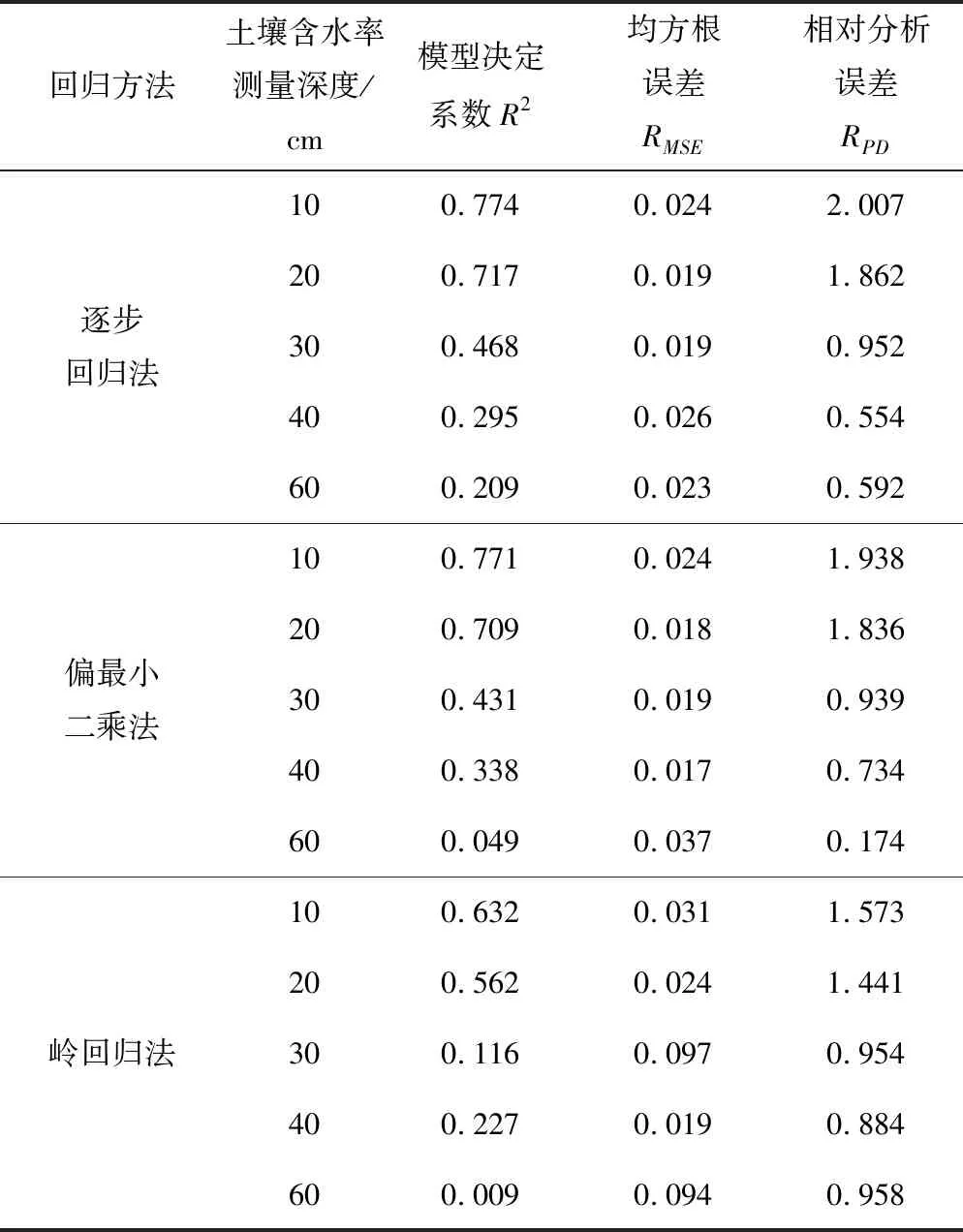
回归方法土壤含水率测量深度/cm模型决定系数R2均方根误差RMSE相对分析误差RPD逐步回归法100.7740.0242.007200.7170.0191.862300.4680.0190.952400.2950.0260.554600.2090.0230.592偏最小二乘法100.7710.0241.938200.7090.0181.836300.4310.0190.939400.3380.0170.734600.0490.0370.174岭回归法100.6320.0311.573200.5620.0241.441300.1160.0970.954400.2270.0190.884600.0090.0940.958

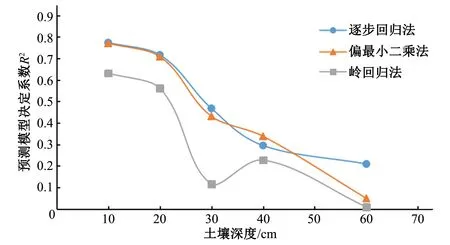
图4 预测模型决定系数与土壤深度变化关系图Fig.4 Relationship between prediction coefficient and soil depth variation of prediction model

由图4可知，各预测模型拟合度R2随土层的加深而下降，在30 cm处皆有明显的折减，对比在30、40、60 cm的验证模型RPD值，都表明在该深度范围内的回归模型不具有预测能力(RPD<1.0)，这也与建模集所得结论一致。

综上，无人机多光谱遥感对作物根域土壤含水率的监测具有一定可行性，利用逐步回归法、偏最小二乘法、岭回归法反演浅层土壤(10、20 cm)的含水率精度较高，这与作物根茎分布长度有关，拔节期的冬小麦根茎长度在10～20 cm居多，大于20 cm的相对较少[21-23]，故难以对较深土壤(h>30 cm)的含水率进行监测。综合比较三种回归方法的建模结果和预测结果可知，逐步回归法模型效果最好，其次是偏最小二乘法，岭回归法效果最差，故在实际应用中应优先采用逐步回归法。

3 结 语

(1)植被覆盖条件下对作物根域土壤含水率最敏感的是波长680 nm的红波段，其次是波长为490 nm的蓝波段，波长550 nm的绿波段和波长720 nm的红边波段的敏感度稍低，波长800 nm和900 nm的近红外波段与土壤含水率的相关性最差，且各波段反射率与土壤含水率的相关性随深度的加深而下降。

(2)在三种回归模型中，逐步回归法只保留显著性较优的波段，拟合度最高，且预测精度最优，偏最小二乘法次之，岭回归法效果最差，所以在植被覆盖条件下通过无人机多光谱遥感监测土壤含水率时应优先采用逐步回归法。

(3)在冬小麦拔节期建立的10、20 cm作物根域处的土壤含水率监测模型具有较高的精度，但对冬小麦其他生长期的土壤含水率反演仍需作进一步探索。本试验研究成果为作物根域土壤含水率最佳监测模型和最佳监测深度的确定提供一定的理论依据，对利用无人机多光谱遥感实现植被覆盖条件下土壤墒情的准确、高效监测有重要意义。