基于长短期记忆神经网络模型的地下水水位预测研究

汪 云，杨海博，徐 建，郑梦琪，韩智昕，赵 耘，赵 耀

(中国冶金地质总局山东正元地质勘查院，山东 泰安 271000)

0 引 言

地下水是地球水资源的重要组成部分，是农业灌溉、工矿业和城市的重要水源之一。但在一定的条件下，比如降雨、蒸发、径流和人工开采等，都会造成地下水位的变化，从而有可能产生地下水降落漏斗、地面沉降等环境地质问题，对生态和人类生产生活造成重大影响。所以，对地下水的动态变化趋势进行研究具有相当重要的意义。

地下水位的变化是一个复杂的自然过程，通过预测地下水位，在一定程度上可以反映出未来地下水的动态变化规律。目前，主要采用数学模型来进行地下水位的预测，应用于地下水位预测的数学模型可分为确定性模型[1]和随机性模型[2]。确定性模型通常应用有限的物理学规律来描述水文过程，是指不包含任何随机成分的模型，只要设定了输入和各个输入之间的关系，其输出也是确定的，该方法需要长期的水文气象资料，对资料数据的数量和精度要求较高，过程较为复杂，计算量较大，模型参数的优选和识别有一定难度。随机性模型应用随机过程描述水文环节，包括回归分析、时间序列分析等，还有模糊识别法、灰色模型、小波神经网络分析等新兴的方法。张展羽等[3]针对地下水位在时间序列上表现出高度的随机性和滞后性，建立了基于主成分分析与多变量时间序列模型耦合的地下水位预报型，将该模应用于济南市陡沟灌区地下水位预测。陆海涛和梁富山[4]将支持向量机应用于地下水位预测中，并与GM(1，1)模型对比。徐强等[5]考虑到BP算法存在极易收敛于局部极小点与过拟合等缺点，构建小波神经网络基础上并引入遗传算法加以优化，以解决上述不足，并与BP和WNN对比预测了天津市深层承压水水位。李慧等[6]针对不恰当地选取RBF神经网络的网络结构和参数会使网络收敛慢的问题，采用粒子群优化算法对RBF神经网络参数进行优化，建立了基于粒子群优化算法的RBF神经网络模型(POS-RBF模型)，对泾惠渠灌区地下水位埋深进行了模拟和预测。徐源蔚等[7]针对地下水位样本之间的相似性及影响因子与地下水位之间具有的确定、不确定性特征，提出将集对分析与相似预测相结合，从同、异、反三方面定量刻画地下水位的当前样本与历史样本之间的相似性，建立了基于集对分析的地下水位相似预测模型。周振民等[8]对GM(1，1)模型的结构进行了研究和改进，选用滦河下游地区节水工程改造后地下水位资料，对滦河下游地区地下水动态进行分析和数值模拟。这些预测模型各具优点，无论是传统方式还是新模型，在实际应用中均取得了一定的成果。但实践表明，单一的预测方式在模拟地下水位复杂的动态特征方面仍旧不可避免地存在着一定的局限性。

神经网络是20世纪80年代以来人工智能领域兴起的研究热点，相比于传统的统计分析模型，具有更好的实时预测性，能够解决多个自变量和因变量的问题，目前广泛应用于地下水位预测中。常见的有BP神经网络模型[9-11]，RBF神经网络模型等[12]。近些年，随着深度学习技术的高速发展，深度学习模型逐渐被应用于时间序列数据的研究中。其中，循环神经网络将时间序列引入神经网络中，使模型在时序数据分析上表现出更强的适应性。但是也存在梯度消失或者梯度爆炸的问题。长短期记忆神经网络模型通过遗忘门和更新门来调控梯度，将反向传播累乘作用变成累加作用解决了梯度消失或爆炸的问题。本文将长短期记忆神经网络模型应用于地下水水位预测研究，以期获得一种更好的地下水位预测方法。

1 研究方法

1.1 RNN循环神经网络

传统神经网络是通过输入层，然后存在隐含层，再到输出层，实现了层与层之间的链接，但是每一层的节点却是相互独立，没有链接的，因此传统神经网络在处理序列数据时，结果往往有很大的偏差。不同于传统神经网络，循环神经网络会对之前的信息进行记忆并应用到当前的输出计算中，即隐含层之间的节点为连接的，并且隐含层的输入包括输入层的输出与上一时刻隐含层的输出。RNN前向输出如图1所示。

图1 RNN前向输出流程注：x表示输入量；h表示隐含层单元；o表示输出量；L表示损失函数；y表示训练集标签；V、W、U表示共享权重系数矩阵。

对于时刻t：

h(t)=f(Ux(t)+Wh(t-1)+b)

(1)

输出量：

o(t)=Vh(t)+c

(2)

模型预测输出：

(3)

式中：soft max为激活函数。

基于处理时序数据的特点，RNN常见训练方法为BPTT算法，训练寻优的参数为V、W、U。但在寻优过程中，可能存在“梯度消失”或“梯度爆炸”现象[13]。

1.2 LSTM神经网络

为解决RNN上述问题，Hochreiter和Schmidhuber于1997年提出了LSTM[14]，通过门控制将短期与长期记忆结合起来，从而在一定程度上解决梯度消失的问题，LSTM结构如图2所示。

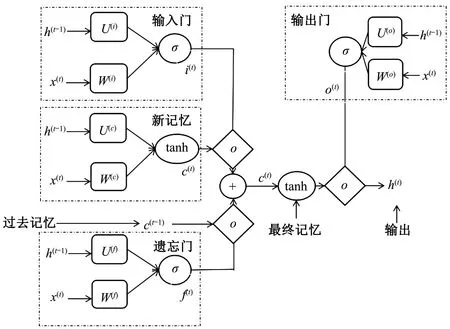
图2 LSTM输出结构

LSTM通过读取h(t-1)与x(t)，输出0或1的数值给c(t-1)中的数字，其中“1”表示保留，“0”表示丢弃，步骤如下：

ft=σ(W(f)·[h(t-1)，x(t)]+b(f))

(4)

式中：h(t-1)表示上一时刻的单元输出；b表示对应的偏置项。

输入门决定着让多少信息加入到单元中，通过sigmoid层的信息决定与tanh层的信息生成，联合对单元状态进行更新。输出门决定着当前单元状态哪一部分信息被输出，依然通过sigmoid层与tanh层完成。输入门步骤如式(5)、(6)、(7)所示，输出门步骤如式(8)、(9)所示[11]：

i(t)=σ(W(i)·[h(t-1),x(t)]+b(i))

(5)

(6)

(7)

o(t)=σ(W(o)·[h(t-1),x(t)+b(o)])

(8)

h(t)=o(t)·tanh(c(t))

(9)

式中：f、i、c、o分别表示遗忘门、输入门、单元状态、输出门；h(t)表示当前时刻的输出；σ、tanh分别表示激活函数sigmoid与双曲正切函数。

2 研究区概况与数据来源

2.1 研究区概况

泰安市地处山东省中部，地理坐标：东经116°04′～118°00′，北纬35°38′～36°29′，总面积7 762 km2，耕地面积316 907 hm2。属于华北暖温带半湿润大陆性季风气候区，多年平均降水量为681.6 mm，多集中在6-9月份，占全年降水量的75%，多年平均蒸发量1 813 mm。境内水系主要属于大汶河水系和淮河水系，地形东高西低，为侵蚀或剥蚀构造地形，海拔37.5～1 532 m；块状地貌是研究区地貌主要特征，断块山与断陷盆地发育，按地貌成因，可划分为侵蚀构造中度切割中山，侵蚀、剥蚀、溶蚀低山，侵蚀、剥蚀、溶蚀丘陵，剥蚀堆积山前倾斜平原，山间盆地冲积平原和黄河冲积平原6种类型。

研究区地层由老到新分属太古界侵入岩及变质岩系(Ar、)，古生界寒武系(∈)、奥陶系(O)，上古生界石炭系(C)、二叠系(P)，中生界侏罗系(J)、白垩系(K)，新生界古近系(E)、第四系(Q)。区内地质构造较为发育，有泰山和徂徕山复式背斜，泰山断裂、新泰-蒙阴断裂、蒙山断裂、南留弧型断裂、夏张断裂、肥城弧型断裂。研究区地下水类型可划分为松散岩类孔隙水、碎屑岩类孔隙裂隙水、碳酸盐岩类裂隙岩溶水和基岩裂隙水。研究的泰安市岱岳区满庄镇姜家园村046J地下水属于松散岩类孔隙水，水位变化主要受气象因素影响。

2.2 研究数据来源

地下水位数据为地处泰安市岱岳区满庄镇姜家园村046J地下水监测井。选取2001-2016年该井逐月平均地下水位观测资料和该地气候数据作为研究数据，地下水位变化如图3所示。

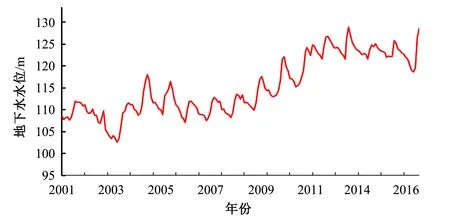
图3 镇姜家园村046J井历年地下水位变化

3 地下水位预测模型构建

3.1 模型框架

根据地下水水位的时空变化特点以及循环神经网络从简设计的原则，本研究构建的预测模型框架如图4所示，该框架大致可分为输入层、隐含层、模型训练、输出层4个部分，各模块功能如下。

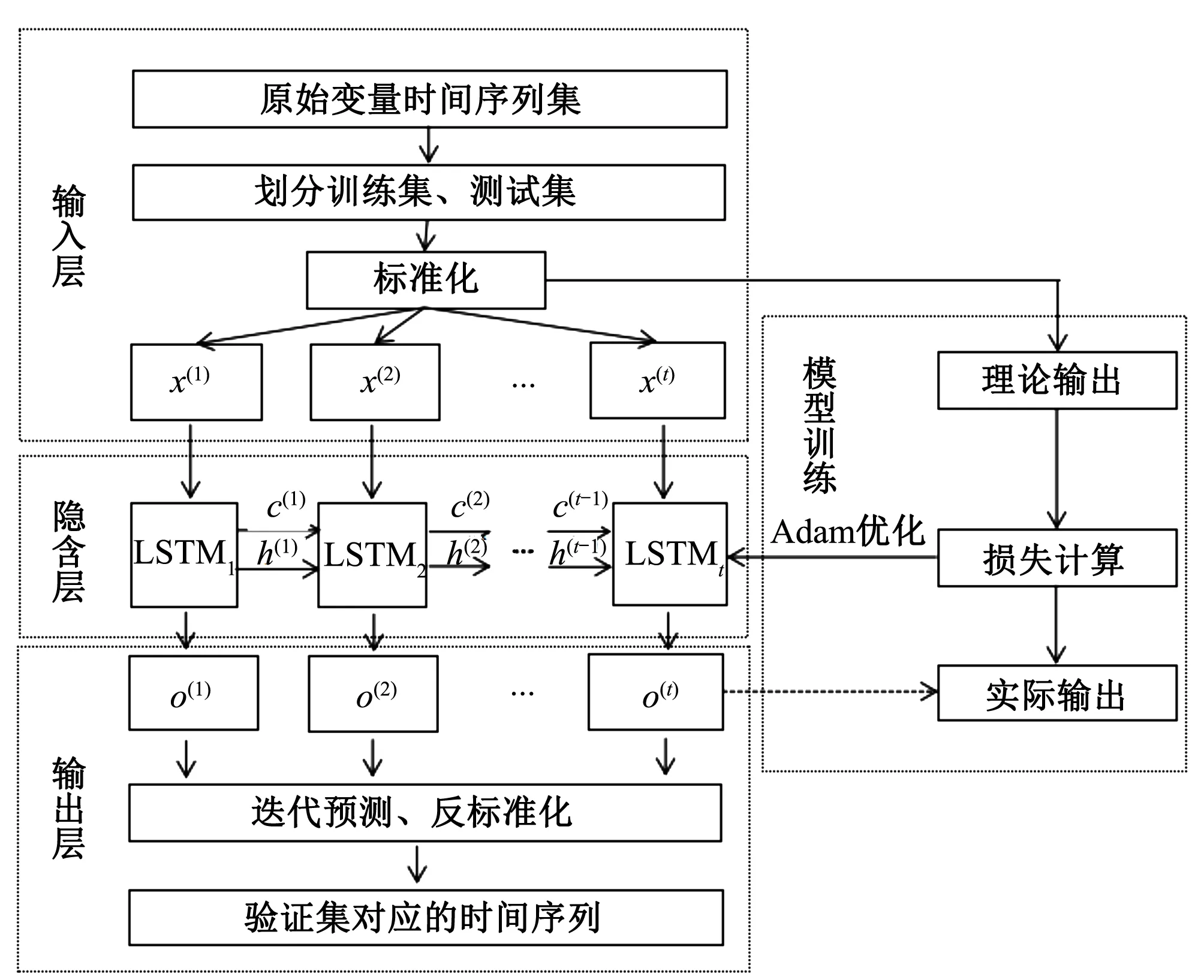
图4 LSTM预测模型结构图

3.2 数据预处理

为消除量纲及数量级的影响，提高模型预测精度，加快模型训练收敛速度，需要对原始变量时序集进行标准化处理，公式可表示为：

x*=(x-xmin)/(xmax-xmin)

(10)

式中：x*表示标准化后的值；x表示标准化前的值；xmax表示原始数据集中最大值；xmin表示原始数据集中最小值。

3.3 模型训练

根据LSTM模型结构，网络训练步骤如下：

(1)在输入层中，定义原始变量数据集为：

Fn=(x1,x2,…,xt,…,xn)

(11)

式中：xt=(at,bt,ct,dt,et,ft,gt),at,bt,ct,dt,et,ft,gt分别表示t时刻对应的地下水位、蒸发量、降雨量、气温、气压、相对湿度、日照时长。

(2)划分训练集与测试集，并对原始变量数据集按照式(10)进行标准化处理，可表示为：

(12)

(13)

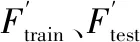
X={x1′,x2′,…,xL′}

(14)

X(t)={xt′,x(t+1)′,…,x(m-L+t-1)′} 1≤t≤L,t,L∈N

(15)

(4)隐含层理论输出为：

Y={y1,y2,…,yL}

(16)

Y(t)={y(t+1)′,y(t+2)′,…,y(m-L+t)′}

(17)

实际输出为：

P={p(1),p(2),…,p(L)}

(18)

P(t)=LSTM(x(t),c(t-1),h(t-1))

(19)

4 实例验证

将上述训练好的模型进行地下水位预测，选取2001-2014年地下水位、蒸发量、降雨量、气温、气压、相对湿度、日照等数据作为训练集，2015-2016年数据作为预测集，模型预测精度以均方根误差作为评价指标。

首先固定非关键参数取值，选择批次大小为168，根据地下水水位变化特点，选择时间步长为12，确定重复训练次数为1 000，其次确定重要参数的范围以简化调参过程，隐含层节点数经验公式如下式所示，学习率一般按3的倍数来调整。

(20)

(21)

式中：m为隐含层节点数；n为输入层节点数；l为输出层节点数，a∈[1,10]，a∈N。因此，隐含层节点数m∈[3,13]，学习率lr∈{0.001,0.003,0.01,0.03,0.1,0.3}。相关组合均方根误差如表1所示。

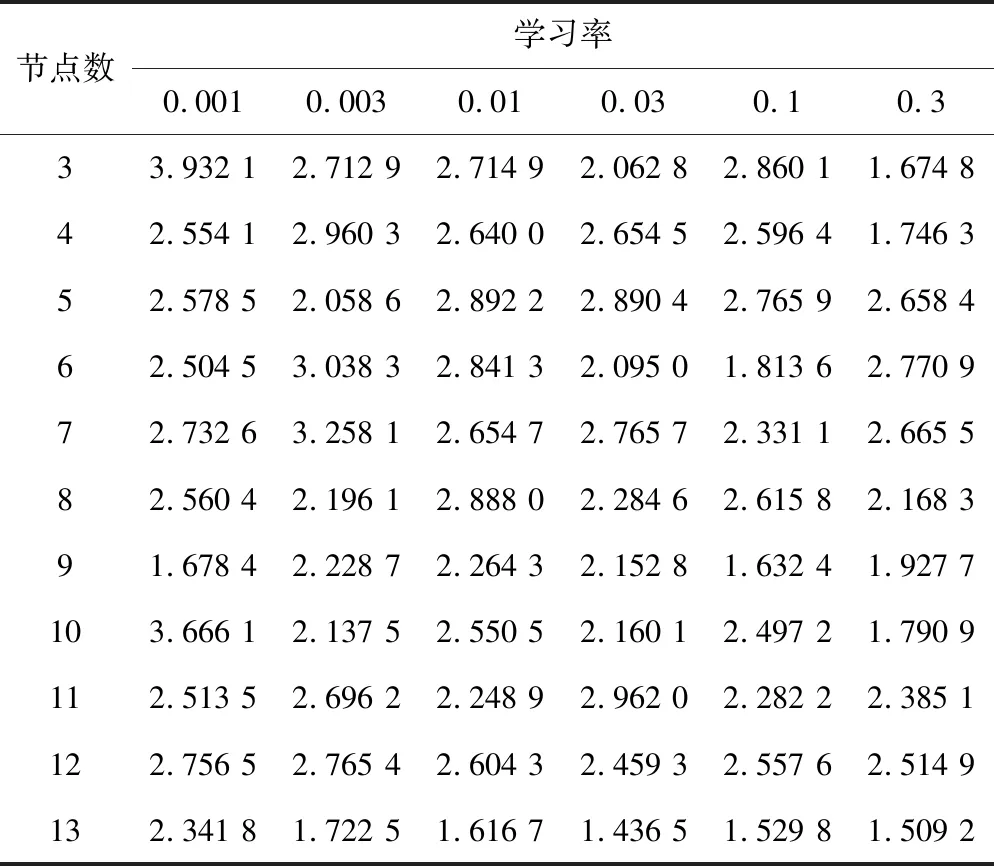
表1 相关参数组合对应误差

由表1可得，当lr=0.03，m=13时，均方根误差最小，为1.436 5，选取该参数对模型训练，整个训练、预测过程在python环境中进行。

为验证多变量LSTM神经网络预测地下水水位的优点，本章节使用单变量LSTM神经网络、BP神经网络对地下水水位进行预测，并作对比分析，已有大量学者对BP神经网络做研究，本章不再赘述，其中，单变量LSTM神经网络仅以地下水水位作为变量输入，三者训练期、预测期拟合曲线如图5、6、7所示。

图5 多变量LSTM预测结果

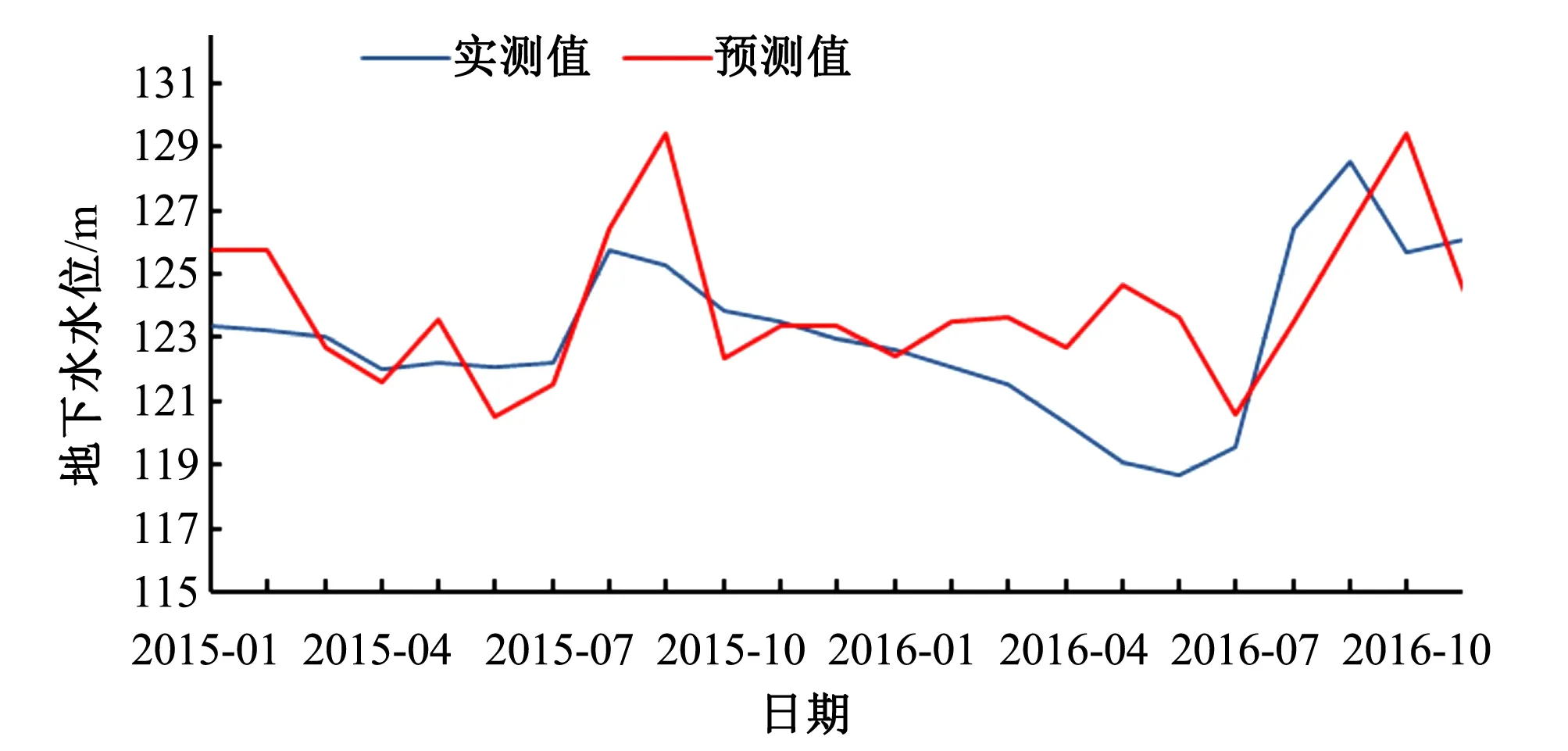
图6 单变量LSTM预测结果

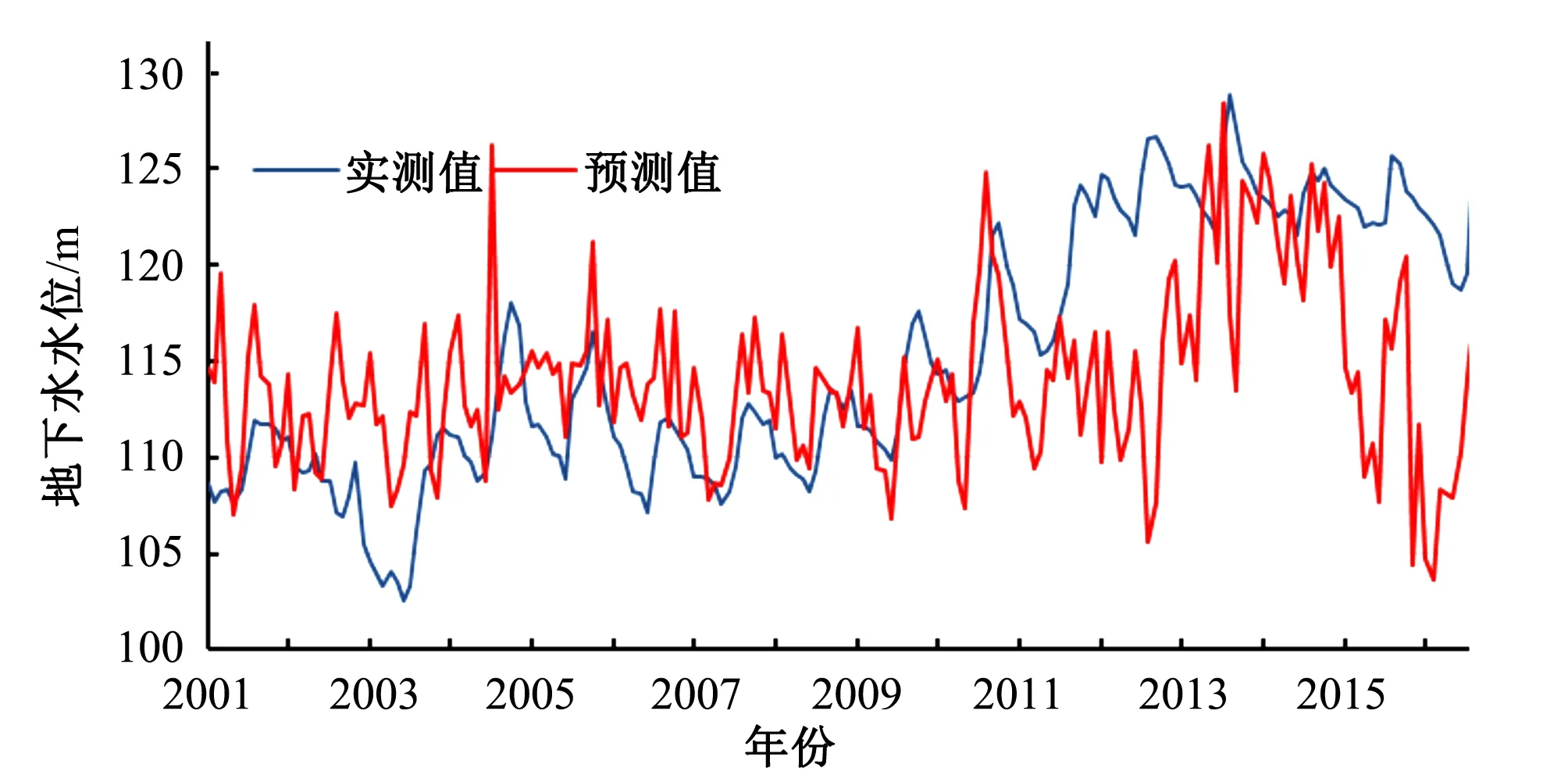
图7 BP神经网络预测结果

由预测结果可知，多变量LSTM模型的预测精度高于单变量LSTM模型、BP神经网络模型，且拟合程度也较为理想，得益于多变量LSTM对时间序列训练的同时，引入了的相关影响变量。单变量LSTM模型仅能对时间序列训练，当外界条件有较大变动时，预测精度将受到较大影响，因此单变量LSTM模型的拟合、预测曲线呈现出较为平稳的周期性变化。BP神经网络预测结果往往取决于经验值，因此在训练期拟合曲线趋势大致与历史相近，但对于未来水位的预测误差很大，究其原因，主要是历史训练数据过少且无法学习历史时序规律。基于多变量的LSTM预测模型拟合曲线并不完全完美，在某些峰值处误差较大，特别是在地下水水位变化规律出现波动时，但总体效果较为稳定。分析地下水水位变化曲线可知，研究区的地下水水位变化规律性较差，剖析其原因，最大影响因素为降雨量的变化波动较大，其他影响变量波动则较为平缓，地下水水位与降雨量的动态变化如图8所示。分析两者动态变化规律可知，研究区地下水水位的变化往往滞后于降雨量的变化，且降雨量变化规律与水位变化规律基本一致，充分说明了降雨量是影响该地区地下水水位的重要因素。曲线中2010-2016年降雨量略小于过去几年，地下水水位却高于往年，分析其原因可能是由于人工开采量的减少导致水位的上升，在没有开采量数据的情况下，预测精度依然较高则是因为LSTM预测时，考虑周边影响变量的同时，也考虑了历史数据的时空变化规律，也说明了研究区近年地下水开采量变化较为稳定，没有发生突变。

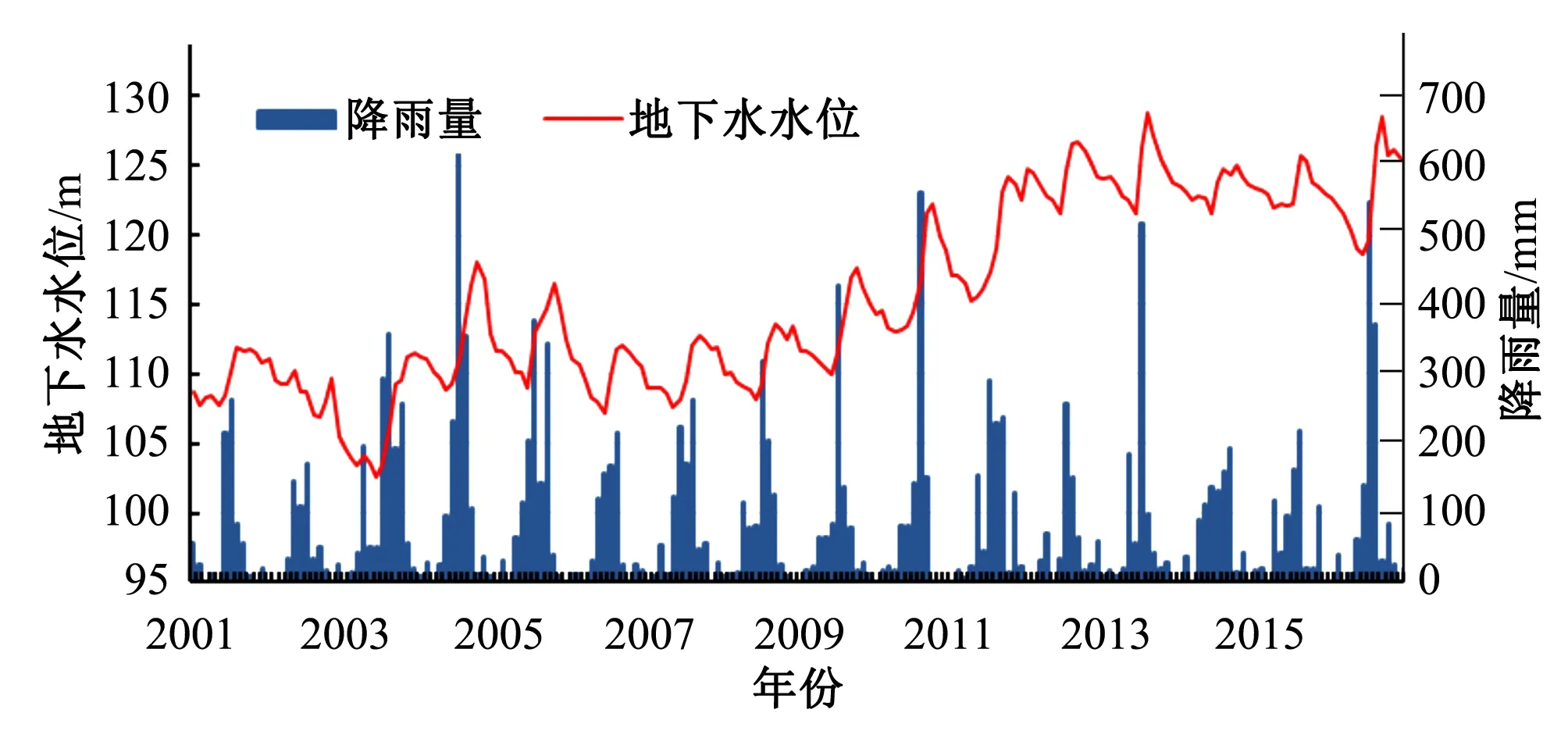
图8 地下水水位与降雨量动态变化

5 结 语

通过构建基于长短期记忆神经网络(LSTM)的地下水水位预测模型并与BP神经网络预测模型与单变量LSTM预测模型对比，得出以下结论。

(1)基于多变量的LSTM神经网络模型可以作为预测地下水水位动态变化简单有效的工具，特别是在一些水文地质资料比较匮乏的地区。

(2)在少量历史数据的情况下，基于多变量的LSTM预测模型亦能做到有效的预测，而且对历史数据重模拟的拟合效果较为理想。单变量LSTM预测模型仅仅呈现出周期性变化，同时存在较为严重的滞后性，无法为一些外界条件变化较大的地区提供水资源管理参考。BP神经网络对历史数据学习性比较强大，但对于未来地下水水位的预测则需要大量的历史数据训练作为支撑。

(3)地下水水位动态变化与气候、下垫面等自然因素相关的同时，很大程度上还受人工开采量的影响，若在缺乏开采量资料的地区进行预测，且研究区开采量波动较大时，就会影响模型原有的预测模式，使预测结果产生较大偏差。