中考数学二次函数综合题的策略研究

渠秋艳

(江苏省徐州市丰县和集初级中学 221700)

二次函数综合题难题大、综合性强，对于学生考查的方向和知识面也相对较广.纵观近几年全国各地中考数学试卷的出题点及考查方向，也恰恰体现出了对学生核心素养能力的追求.我认为初中数学教师在数学素质化教学管理中，应立足核心素养全局视角，结合学生特点来传授、引导二次函数综合题的解题策略和现实技巧.纵观全国范围内，各省市地区中考数学中二次函数是核心考查点，并作为载体以综合题的形式全面考查学生初中数学知识掌握情况.下面通过具体的题目分析二次函数综合题解题思路与方法.

原题呈现：如图1，直线x=-4与x轴相交于点E.一条过原点O的抛物线与x轴上OE线段相交于点A，且与直线x=-4相交于点B.过点B的一条直线与x轴平行，与抛物线相交于点C，且直线OC与直线AB相交于点D.AD∶BD=1∶3.(图1)

①：求图中点A的坐标(x,y);

②：假设图中三角形OBC为等腰三角形，求图中抛物线的表达式.

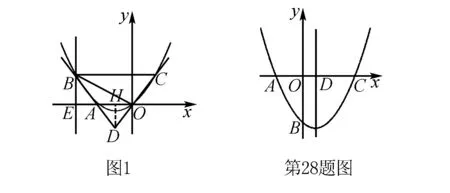
对于此题，正如上述所言，以二次函数作为载体，考查点比较多.这类题目，对于绝大部分学生来说，第一印象也不陌生，只要熟知数学课本教材中的知识体系和公式概念等，基本都能够在较短的时间内进入到正题思路，即能够大体知道本题目考查的知识方向，然后结合教师传授的解题思路和思考方式来解题.

在解题中，首先明白这是一道二次函数题目，所以题目中关于二次函数的关键信息和已知条件显得很重要.具体来看，最先利用二次函数的对称性.其次，题目中给出的各项信息相对繁琐，需要学生花费一些时间尽快将这些繁琐的信息整理起来，即挖掘所有的隐含条件.快速整理之后，对各方已知条件在内心已经有一个大体的认识和梳理，譬如，D是BA和CO延长线上相交于抛物线的一个点，并且处在抛物线的对称轴上.如图1所示，依据已知条件推理演算，创造更进一步的条件，即离答案更进一步的有利条件.此处，实际上考查的是平面几何知识，并且学生本人也基本清楚.再加上题目的最后给出了直线比例关系，所以，可过点D作一条与x轴垂直的直线，即可构造出一对相似三角形.如此以来，即可求出A点的具体坐标.

随着点A坐标答案成功计算得出，借助直线、点等彼此间的位置关系和比例关系，各点的位置以及直线长度同样可轻松计算得出.如此以来，直接代入抛物线公式y=ax2+bx即可.

如上所述，关于数学解题，本身就是课堂教学的重要组成部分，因为各项教学活动的开展和实施，本身就是围绕着如何让学生自主解决和思考问题、寻求答案.具体来看，二次函数章节内容的教学管理中，也基本围绕着学生如何解题来展开.但是，核心基础始终不变，即围绕着函数性质、方程与数学模型等.以近两年全国多地的中考数学来看，二次函数综合题的考查点主要集中在建模思想、最值问题、几何关系、树形结合、问题转化等.严格讲，侧重点在于数学问题中的思路创新.譬如，对于部分学生而言，几乎什么样的题目都能够快速进入正确思路，并给出答案，而对于大部分学生来说，短时间内并不会认清问题所在，也无法迅速准确进入正确思路.反之，对于我们潜意识中的优秀学生来说，很多题目也都属于新题，但是这部分学生已经具备了综合分析和解决问题的能力，即发散性的数学思维和快速的推演逻辑.以上述中考原题为例，其属于相对简单的题目，并且考查点并不算多.本处再次以2016年某地中考的一大难题为例，做进一步思路数理.

(1)求二次函数的表达式及其顶点坐标；

(3)M(s，t)为抛物线对称轴上的一个动点．若平面内存在点N，使得以A、B、M、N为顶点的四边形为菱形，则这样的点N共有____个；

对于本题，正如前文所分析，旨在侧重学生的数学思路，更加直接一点说，就是如何创新解题技巧.实际上，本道题和第一道题并无本质区别，均是以二次函数为载体，唯一的不同就是考查点纵横延伸，即考查的宽度以及问题的深度.

与第一道题不同，问题方向并未发生改变，均是要求求二次函数表达式，但给出的解题工具和知识内容却发生了变化，所以解题思路方面也应当调整.对于第一问和第二问，基本可参照例题1的解题思路来解决.对于第三问，属于反证的题型，给出的答案和已知条件，要求学生来证明答案的正确性.是否存在点N使得四边形ABMN成为菱形.故此，可直接将四边形ABMN当成菱形，结合点M及其可能的坐标位置，先行求出ABM三点和线之间的位置关系，即AB和AB等长.如此以来，即可将具体问题抽象化.添加辅助线，并结合平面几何相关定理和公式.由于已经知道M点有5个，那么对应的N点也应当是5 个.将抽象问题具体化、将繁琐问题简易化，整个过程本身就是方程思想形成过程.