眼中有“式” 心中有“数”——以《代数式1》教学为例

孙 明

(江苏省常州市新北区龙虎塘中学 213000)

一、教材解析

本节的主要任务是：引导学生去探究和分析现实生活中各种事物之间的数量关系，将这些关系用代数式表示出来.了解代数式在人类的学习、生产和生活中的重要意义.本节的重点是让学生弄清事物之间的数量关系，并用代数式将这些数量关系准确的表示出来.

二、目标预设

1.了解代数式的意义，能根据简单的数量关系列代数式.能用语言描述代数式的意义，并能解释一些简单代数式的实际背景或几何意义，进一步发展符号感.

2.经历探索事物之间的数量关系并用代数式表示过程，体会特殊到一般的辨证思想和代数式的模型思想.

三、设计理念

根据建构主义理论，学生的学习是在已有知识基础上的一步步自我建构，在字母表示数的基础上升到代数式自然过渡并不断深化.本节课，我对教材的处理是先从简单实际问题着手，让学生感受代数式的必要性，简明性，一般性，从而归纳出代数式定义，对代数式进行辨析和编写；其次从数的角度，形的角度，规律的角度再次对代数式深刻理解.最后，从逆向思维上让学生对着代数式说数学含义及实际意义.

四、教学设计

板块一、根据实际情景列式

问题1：下面是某年十月份的日历，根据以下情景，列出式子

(1)日历中各涂色方框里的4个数，它们之间有怎样的关系?(同伴相互说一说)

(2)你能简明地表述你发现的规律吗？(独立思考后，同伴相互说一说)

(3)如果用字母a表示方框里的任意一个数，试着写出其他三个数，并与你的同伴交流.(独立完成后，同伴互纠)

教师巡视后展示学生的各种不同方式：

问题2 下图是由长方形和正方形拼成的大正方形

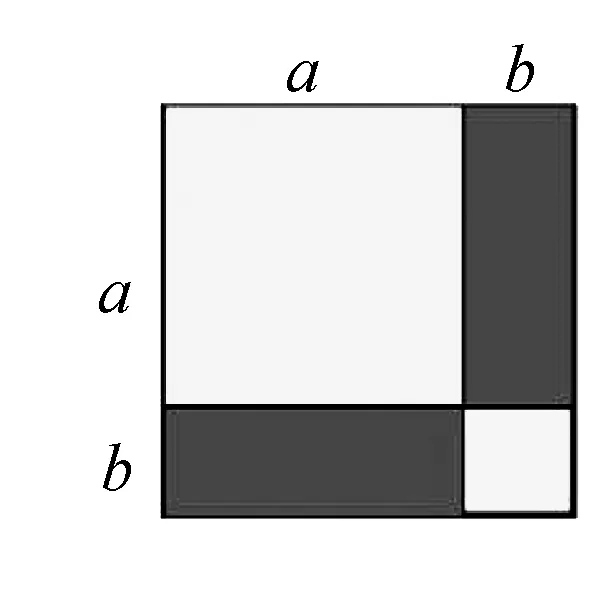
(1)图中大正方形的面积如何表示？(独立完成后，同伴互纠)

归纳：几何图形面积的不同算法

(2)你有何发现? (同伴相互说一说)

归纳：从几何情境中得出代数公式

问题3 弹簧挂上物体后会伸长，已知一弹簧的长度(cm)与所挂物体的质量(kg)之间的关系如下表：

物体质量012345弹簧长度1212.51313.51414.5

(1)当物体的质量逐渐增加时，弹簧的长度怎样变化?(一学生独立回答)

归纳：当物体的质量逐渐增加时，弹簧的长度越来越长.让学生感受现实世界中变化的数量及其关系，感悟函数思想.

(2)如果物体的质量为xkg，弹簧的长度如何表示？(独立完成后，同伴互纠)

归纳：弹簧长度为(12+0.5x)cm，由具体到一般，从具体情境中抽象出数学模型.

设计意图：板块一，根据实际情景列式从三个方面入手：从数的角度、从几何图角度、从函数角度.从日历上4个数之间的关系，让学生明白上升到字母表示数的必要性、简明性、一般性.从几何图形着手，让学生感受数形结合，形中有数数中有形.弹簧长度随重物的增加而增加，渗透函数思想.例题的选择贴近学生的实际，每个学生都能去写一写，说一说.增加学生学习的兴趣，让课堂讨论的氛围热烈.

板块二、理解代数式的定义

问题1:观察我们列出的这些式子以及上节课所列出的式子有何共同的特征？(同伴讨论)a-1,a+6，a2+2ab+b2，(a+b)2，12+0.5x.

归纳共同特征是：用运算符号将数字和字母连接的式子。(学生代表发言)

教师归纳：像这样的式子就是代数式，单独的一个数或单独的一个字母也是代数式.

讨论：a2+2ab+b2=(a+b)2，a

小结：代数式中不含“=”、“>”、“<”、“≥”、“≤”、“≠”等符号．

代数式书写注意事项：

1．数与字母相乘，可省略乘号，数字写在字母前面，若数字是带分数的应写成假分数．

2．除法运算通常写成分数的形式．

3．结果是和或差的形式时，应将式子用括号括起来，再写上单位名称．

问题2：判断下面的是代数式吗？(独立完成后，同伴交流)

(1)0 (2)1<3 (3)x=1 (4)x2-1

问题3：请根据下列数字和字母，自己编写几个代数式，请你的同伴判断是否正确.

a，8，b,s,t,40,m,n

设计意图：学生根据几个式子共同讨论出代数式具备的共性，不难得到.问题2结合代数式定义也可以很快判断出，一般教师到这里就结束了.其实，学生是否真能理解单独的数，单独的字母都也是代数式，以及代数式的书写规范是否能注意等问题该如何设计？因此，我设计了问题3，自己编写代数式，并请同伴判断是否正确.将知识点综合运用的同时，激发学生的思维和兴趣.

板块三、进一步理解代数式的意义

问题1：在月历中任意圈出同列中相邻的三个数，说说三个数的关系；若设其中一个数为a，用含有a的代数式表示这三个数.(同伴相互说一说)

问题2：用代数式表示图中空白部分的面积.(独立完成后，同伴互纠)

(教师巡视后，收集学生资源，让学生展示)

问题3：剪绳子.(动手操作后，小组交流)

(1)将一根绳子对折1次后从中间剪一刀，绳子变成____段；将一根绳子对折2次后从中间剪一刀，绳子变成____段；将一根绳子对折3次后从中剪一刀，绳子变成____段.

(2)将一根绳子对折n次后从中剪一刀，绳子变成____段.

(教师巡视，参与小组讨论，个别点拨，找典型资源呈现)

设计意图：进一步理解代数式，在三个方向进行：数学方面，几何图形方面，规律方面.

板块四、课堂小结

1. 请根据代数式的定义，编几个代数式；并说说代数式的注意点.(同伴相互说一说)

2．将你的代数式赋予一个实际意义.

归纳：注意运算顺序，代数式可以简明地描述许多实际问题中的数量关系.许多不同背景实际问题中的相同数量关系可以用同一个代数式表示.

设计意图：课堂小结以问题的方式提出，既有知识的回顾也有知识的延伸，为下节课作铺垫.