基于正交试验和神经网络的堤防边坡抗滑稳定可靠度研究

(河海大学 力学与材料学院，南京 211100)

1 研究背景

水利工程中，堤防边坡安全一直是工程界所关注的热点问题，其中堤防边坡失稳是最常见的破坏形式之一[1]。传统方法采用安全系数来描述堤防边坡的失稳破坏问题，通常把影响堤防边坡安全的因素，例如黏聚力、内摩擦角、弹性模量等看作确定性因素,然而，实际工程中这些因素多数都是服从某种概率分布的随机变量[2]。鉴于此，可靠度理论广泛应用于研究边坡的安全问题。

结构可靠度理论的传统方法有一次二阶矩法、改进的一次二阶矩法、二次二阶矩法、二次四阶矩法、响应面法和蒙特卡洛法等方法。一次二阶矩法又叫作中心点法，其概念清晰，计算简便，但由于没有考虑随机变量的概率分布导致其计算精度不高[3]。改进的一次二阶矩法又叫做设计验算点法，该方法在一次二阶矩法的基础上考虑了随机变量的概率分布，但此2种方法对于结构功能函数呈现高度非线性时，会产生较大误差。二次二阶矩法和二次四阶矩法虽然能进一步提高非线性功能函数时的计算精度，但其计算相对比较复杂，且只适用于功能函数偏导数能够由解析法求解的工程问题[4]。同时，这些方法也只适用于结构功能函数能够显式表达的情况，然而复杂结构往往不能给出功能函数的显式表达。响应面法能够合理地拟合复杂结构的功能函数，但在进行结构可靠度计算的插值迭代过程中，每次迭代都要寻找新的验算点来拟合响应函数，相对来说比较繁琐。复杂结构直接采用蒙特卡洛法的计算结果精确，但计算成本昂贵[5]。

近年来随着人工智能算法的发展，采用人工智能算法得到复杂结构的代理模型，既能较精确地逼近功能函数，又避免了在可靠度迭代计算过程中的多次拟合问题。故本文采用BP神经网络方法训练模型代理堤防边坡失稳可靠度计算的功能函数，结合蒙特卡洛法进行失效概率计算。

2 正交试验—神经网络的堤防边坡可靠度分析方法

2.1 正交试验

堤防边坡失稳过程一般是由多因素导致的，当多因素多水平试验组合较多时，如果采用全面试验往往需要耗费大量的时间和成本，有时候则是不可能完成的任务。正交试验则能够选取合理的样本数达到较好的试验效果，正交试验的有力工具是正交表，正交表是已经规格化、标准化的表，可直观地应用于试验设计[6]。

以L9(34)为例解释正交表代号的各字符含义，L为正交表的代号，表示正交表；9代表正交表的行数，数字表示本例必须完成的试验次数为9次；3表示正交表中的字码数，本例中表示1个因素要安排3个水平；4代表正交表的纵列数，指最多可安排的因素数，即本例中最多可安排4个因素。

由正交试验得到的样本点可以进一步做极差分析来评判各因素对试验结果影响程度的大小，判断各因素对实际结果的敏感性。Rj为第j列因素的极差，即第j列因素各水平下的指标值的最大值与最小值之差，即

Rj=max(Kj1,Kj2,…,Kjm)-min(Kj1,Kj2,…,Kjm)。

(1)

式中Rj反映了第j列因素的水平变化时试验指标的变动幅度。Rj越大，说明该因素对试验指标的影响越大。依据极差Rj的大小，可以判断各个因素对试验结果的敏感性。

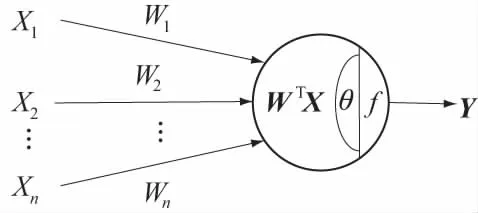
图1 人工神经元

2.2 BP神经网络

BP神经网络是一种以梯度下降为核心的神经网络最优化方法，采用误差逆传播的多层前向神经网络，其基本组成单元为人工神经元，神经元结构如图1所示。

设输入向量为X=(X1,X2…Xn)T，相应的连接权向量W=(W1,W2,…,Wn)T,阈值为θ。(WTX-θ)为神经元的输入信息，神经元输出信息Y可表示为

(2)

式中：WTX为激活值；f(·)为激活函数。激活函数需要满足非线性、可微性和单调性，通常采用sigmoid函数作为激活函数，即

(3)

神经元互联后形成网络，其结构包括输入层、隐含层和输出层3部分。记输入层为第0层，输出层为第N层，隐含层依次为第1层至第N-1层。设第i层(i≥2)的接收值为Zi=WiTYi-1，理想输出值为向量Yi=(Y1i,Y2i,…,Yni)，与实际输出向量S的误差e可用最小平方差表示，即

(4)

式中：j为输出层第j个神经元；Yij为第i层第j个神经元的理想输出值；Sij为第i层第j个神经元的实际输出值。网络的训练泛化能力由决定系数R2表示，即

(5)

式中：SSR表示回归平方和；SST表示总平方和。最小平方差和决定系数可以对神经网络的性能进行评价。

神经网络进行训练过程中，按照误差减少的方向修正权矩阵，权矩阵的调整量δW与本次网络误差e的梯度的负值成正比。为了避免网络学习过程中出现局部最优解，采用BP网络改进算法，在连接权上附加一个权重小量，使网络达到全局最优[3，7]，即

(6)

式中：η为比例系数；μ为区间(0，1)的一个微小数；δWn-1为前一次迭代计算的权矩阵调整量。

2.3 蒙特卡洛法

可靠度理论中，结构的功能函数为Z=g(X1,X2,…,Xn),按照随机变量的已知概率密度函数对随机变量进行随机抽样，计算样本的功能函数值。若得到Z<0，结构失效；Z=0，结构处于临界状态；Z>0，结构安全。模拟过程中失效次数与抽样次数的比值则为结构的失效概率。

根据2.2节内容可以得到边坡失稳的代理模型，本文以边坡失稳的抗滑稳定安全系数fs构造结构的功能函数Z=fs-1。由概率论Bernoulli定理[8]可知，随机事件Z<0在M次独立试验中的频率mf/M依概率收敛于该事件的失效概率pf，即结构的失效概率为

pf=mf/M。

(7)

式中mf表示M次为独立试验中失效的次数。

同时失效概率pf与可靠概率pr有如下关系，即

pf+pr=1 。

(8)

2.4 可靠度计算步骤

正交试验结合神经网络的堤防边坡可靠度分析步骤如下：

(1)确定影响堤防边坡稳定的因素，根据实际情况及经验确定每一种影响因素的水平数，利用对应的正交试验表确定试验样本。

(2)进行确定性分析，比如结构试验或数值分析逐组计算样本点上的试验值。本文采用有限元强度折减法做数值分析。

(3)由正交试验得到的样本点及数值分析得到的样本试验值训练神经网络，训练好的神经网络作为结构的功能函数的代理模型。

(4)对影响边坡稳定的因素按其服从的概率分布采用蒙特卡洛抽样模拟，将抽样样本代入到训练好的神经网络模型中，计算其失效概率及可靠度。

3 算例分析

图2 堤防横截面示意图

本文采用如图2所示某段堤防作为算例。该堤防堤顶高程H=10 m，堤顶宽度B=6 m，坡比为1∶2，土体重度γ=20 kN/m3，黏聚力c=12.38 kPa，内摩擦角φ=20°，弹性模量E=100 MPa，泊松比v=0.35。这里考虑c，φ和E为相互独立服从正态分布的随机变量，变异系数为0.1，其余参数为定值。

3.1 强度折减法计算堤防边坡抗滑稳定安全系数

边坡抗滑稳定安全系数常用的计算方法有极限平衡法和强度折减法。本文采用强度折减法计算边坡抗滑稳定安全系数。强度折减法不需要提前预设边坡失效的滑弧面且计算的假设条件比较少，使用较为广泛[9-10]。强度折减后的黏聚力和内摩擦角有以下关系：

c′=c/fs，

(9)

φ′=arctan(tanφ/fs) 。

(10)

式中：c和φ分别为土体所能提供的抗剪强度参数，黏聚力和摩擦角；c′和φ′分别为折减后土体抗剪强度参数；fs为强度折减系数。计算中假定不同的强度折减系数，当达到某一强度折减系数，边坡达到抗滑稳定临界状态，则认为该强度折减系数为边坡的抗滑稳定安全系数。通常认为土坡达到抗滑稳定临界破坏的判断标准有以下3个[11-12]：①以计算结果是否收敛作为评价标准；②以某特殊关键位置的位移突变作为评价标准；③以边坡塑性区最终是否贯通作为评价标准。

本算例采用有限元强度折减法计算该堤防边坡抗滑稳定安全系数的过程中，本构模型采用Mohr-Coulomb强度准则, 抗滑稳定临界破坏判据采用关键点的位移突变作为依据。该算例抗滑稳定安全系数的计算结果为1.212。该方法计算结果的塑性区贯通时的塑性应变(PEMAG)以平均阈值75%进行光滑处理，如图3所示。最终堤防边坡失效时的位移云图(Umagnitude)如图4所示。

图3 塑性区贯通时的塑性应变云图

图4 堤防边坡失效时的位移云图

3.2 采用正交试验选取训练样本点

选取堤防边坡土体黏聚力、内摩擦角和弹性模量三因素、五水平进行正交设计试验。试验点逐组采用有限元强度折减法进行有限元堤防边坡抗滑稳定安全系数计算，见表1。正交表采用L25(56)进行设计，共计试验25次。极差分析结果见表2。

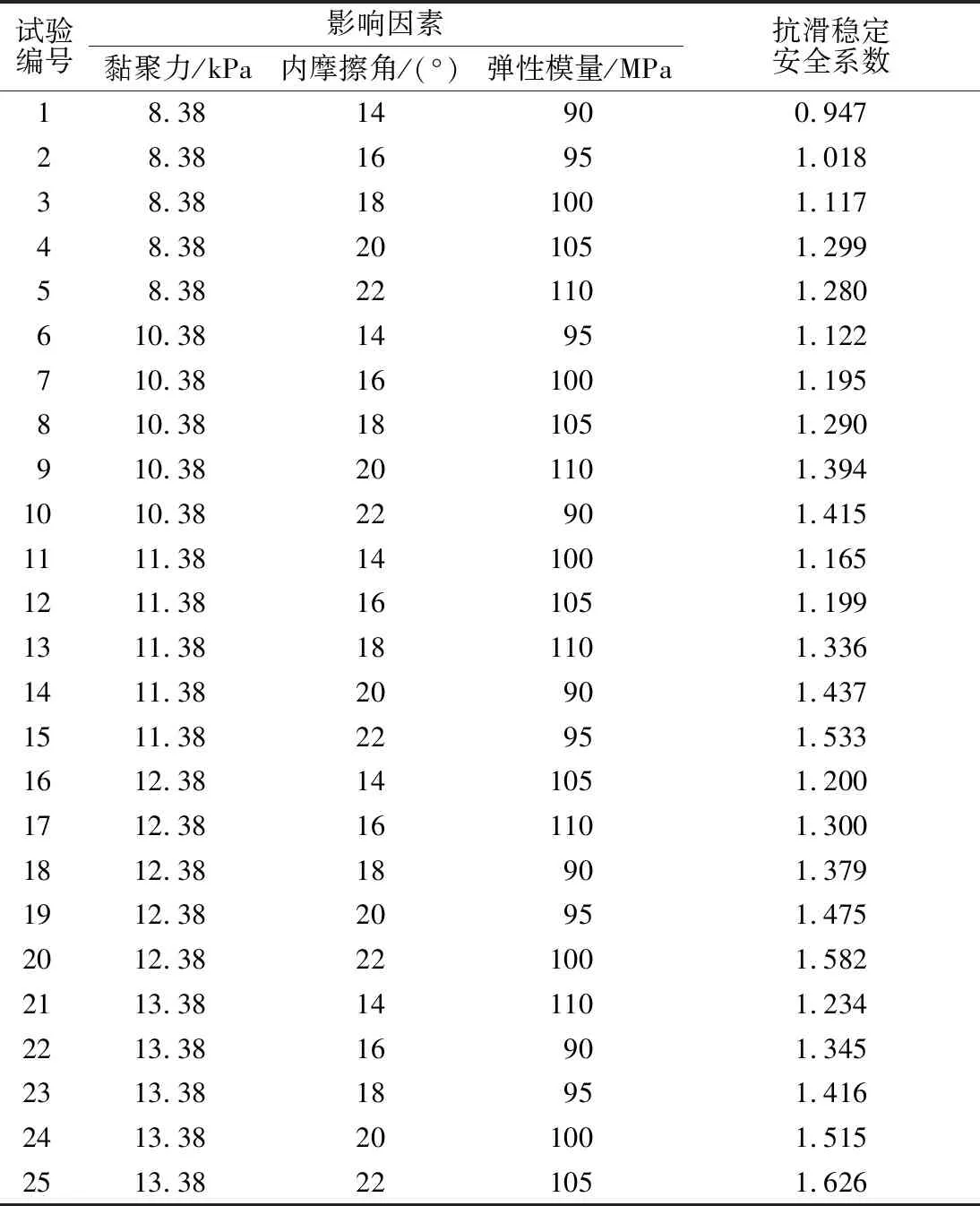
表1 正交试验选取神经网络训练的样本

表2 极差分析结果

由表2可知随机变量内摩擦角、黏聚力和弹性模量的极差关系为R2(1.768)>R1(1.475)>R3(0.051)，表明土体的内摩擦角和黏聚力对边坡安全系数影响较大，而弹性模量对边坡安全系数影响很小。

3.3 神经网络训练功能函数的代理模型

由BP神经网络训练得到结构功能函数的代理模型。网络训练过程采用Levenberg-Marquardt算法，该算法是非线性最小二乘法的一种优化算法，同时具有梯度法和牛顿法的优点。文献[13]推荐隐含层神经元个数为8～15，模型整体预测结果精确，经过试算，本算例隐含层神经元个数取10时误差较小，决定系数为0.987，最大误差为0.087。网络训练过程中，由3.2节正交试验和极差分析结果可知，边坡稳定的影响因素主要为内摩擦角和黏聚力，弹性模量对结果影响很小。故本文采用输入层—隐含层—输出层为2-10-1的结构，2代表输入层输入参数的个数，即黏聚力和内摩擦角；10代表隐含层神经元个数；1代表输出结果，为堤防边坡抗滑稳定安全系数。由神经网络模型得到的抗滑稳定安全系数与随机变量的响应函数为fs=g(c，φ),进而构造出堤防边坡失稳的功能函数为

Z=fs-1=g(c，φ)-1 。

(11)

3.4 蒙特卡洛法计算堤防边坡抗滑稳定可靠度

正交试验考虑内摩擦角和黏聚力2个随机变量为影响因素。按照如表3所示随机变量的统计特征，以平均值为中心，3倍标准差为取值范围选取随机数。采用蒙特卡洛法随机生成样本，然后将生成的样本输入到3.3节中训练好的神经网络模型及式(11)所示的功能函数进行堤防边坡抗滑稳定可靠度的计算。以往的研究表明[13]，当模拟样本数M>5万时，误差趋于稳定且较小。为保证精度,本算例分别进行M=10万，50万，100万3组抽样计算，每组数据抽样10次取平均值进行比较，其结果如表4所示。由Bernoulli大数定理可知，独立随机事件发生的频率收敛于该事件概率，即当抽样次数取到100万次时，由式(7)得到堤防边坡抗滑稳定的失效概率为pf=5.706%。

表3 参数的统计特征

表4 3组抽样的结果

4 结 论

本文提出了以神经网络训练模型代替边坡抗滑稳定失效的功能函数，结合蒙特卡洛法对随机变量抽样计算，得到边坡抗滑稳定失效概率的计算模型，其主要结论如下：

(1)以某堤防边坡失稳破坏为例，考虑黏聚力c、内摩擦角φ为独立的随机变量，采用正交试验和强度折减法，通过非线性有限元法计算得到神经网络训练的样本点及试验值，建立了堤防边坡失稳预测的神经网络模型。

(2)根据随机变量的统计特征，采用蒙特卡洛法进行抽样，由训练好的神经网络模型进行堤防边坡抗滑稳定的可靠度计算，为堤防边坡失稳破坏的预测提供了新路径，且方法原理简单，操作方便。

(3)通过算例表明，自重作用下堤防边坡的抗滑稳定安全系数随着土体黏聚力和内摩擦角的减小而减小，弹性模量的变化对其影响不大，这也符合岩土工程中，边坡稳定影响因素主要由黏聚力和内摩擦角为主导因素的认知。