基于随机力学理论的堤防安全分析方法综述
(1.河海大学 力学与材料学院,南京 211100; 2.河海大学 机电工程学院,江苏 常州 213022)
1 研究背景
堤防工程是指沿河、湖、海岸或分洪区、围垦区等边缘修筑的挡水建筑物,是防洪工程的重要组成部分。据全国水利发展统计公报,截至2017年底,全国已建成的江河堤防保护人口6.1亿,保护耕地4.1千万hm2。影响堤防安全的因素众多,如堤身材料不均匀、堤基结构复杂,堤防及其构筑物性状演化,渗流及河流冲刷动态作用,人类与动植物活动影响等。遭遇洪水时,一旦堤防发生险情将严重威胁该区域附近的财产及人身安全,因此需要对堤防进行安全分析。
在现行的堤防工程设计规范中,堤防安全分析主要基于确定性的方法[1]。采用此种方法进行分析时,风险因素或相关参数为确定值,最后得到的结果也为某一定值。然而,堤防安全分析中的水文风险因素、水力风险因素往往具有不确定性。此外,我国堤防的土体地基一般具有明显非均质性和各向异性特征,同时在对土体采样、测量过程中存在误差,这些因素均使得土体参数具有不确定性或随机性。另一方面,土体参数所具有的随机性不是纯随机,而是包含在土体参数整体空间结构性之中的一种内在的随机性,是结构性和随机性的统一。因此土体参数具有空间变异性(不确定性),同时也具有自相关性[2]。《自然科学学科发展战略调研报告》指出[3]:“如果不考虑设计参数的不确定性,结构的精确分析所能取得的效益将被粗略的经验性安全指标所淹没。”因此,在如今的堤防安全性分析中采用确定性分析方法是不满足要求且不合理的。此外,以往的堤防安全分析方法通常忽略了部分风险因素存在的互相关性,导致无法准确地评价堤防的安全性,所以也有必要对风险因素的互相关性进行研究,使其能客观地反映在堤防风险率分析计算中。
为了较好地反映水文、水力等风险因素的不确定性和土体参数的空间变异性与自相关性,同时考虑部分风险因素之间可能存在的互相关性,基于随机力学理论的堤防安全分析方法应运而生,完善了堤防安全分析方法理论。目前,该方法的相关研究较多,但缺少系统性的总结说明。因此,本文对基于随机力学理论的堤防安全分析方法的主要内容及其在堤防工程中的应用进行综述,阐明该方法有待解决的问题及未来研究的方向。
2 堤防失事模式及风险因素分析
2.1 失事模式分析
影响堤防安全的风险因素众多,风险因素之间关系复杂,在进行堤防安全分析时,建立同时考虑全部风险因素的数学模型十分困难。因此,需将堤防失事破坏分为若干失事模式,并按失事模式对风险因素进行分类,以便进行堤防安全分析。目前,对堤防失事风险的分类有许多种,如朱元甡[4]将堤防失事风险分为水文风险、水流风险与工程结构风险3类;王卓甫等[5]将水文风险和水流风险都归为水文风险,即漫顶风险,把堤防失事风险分为水文风险和结构风险2类,其中结构风险包括边坡滑动和渗透变形;陈红[6]]和曹云[7]将堤防失事破坏分为漫顶失事、渗透失事及失稳失事3种典型的失事模式;张骏[8]在上述3种典型失事的基础上增加了行蓄洪破坏;邢万波[9]将堤防失事破坏分为漫溢失事、渗透失事、失稳失事及地震险情。
堤防失事模式是堤防安全分析的基础,失事模式必须是能够代表堤防失事破坏的典型,同时也需考虑失事模式可能产生后果的严重程度,以及建立堤防安全分析数学模型的可能性。因此,在忽略地震险情和行蓄洪破坏等特殊失事情况下,本文将堤防失事破坏分为漫溢失事、渗透失事和失稳失事3种典型模式。其中,漫溢失事包括洪水位高于堤顶导致的漫顶以及波浪爬高导致的洪水漫过堤防。
2.2 风险因素分析
目前,许多学者[6-7,9-11]从堤防的典型失事模式出发,针对堤防工程的破坏类型和破坏机理,深入分析了主要风险因素及其对堤防安全的影响。本文综合考虑相关文献[6,8,10]对风险因素的划分情况,将主要风险因素分为4类:荷载、抗力、隐患情况及加固情况,又将抗力分为堤身特性、堤基特性,以便对风险因素进行分类分析。

图1 堤防漫溢失事风险因素
(1)漫溢失事:漫溢是由于堤防高度不达标、有超标洪水或波浪爬高,造成洪水漫过堤顶。相关文献[6,9-10]分析了漫溢失事的风险因素,本文综合考虑后得出漫溢风险因素是洪水位、波浪爬高、堤防等级及堤顶高程,见图1。
随着防洪标准的提高及对已存堤防普遍进行加高加宽,漫溢失事概率大大减小。
(2)渗透失事:渗透失事是指当迎水面与背水面间的渗透坡降大于临界渗透坡降时,产生的堤坡冲刷、漏洞、接触冲刷、管涌、流土等类型的渗透破坏。相关文献[6-7,9-11]分析了渗透失事的风险因素,如表1所示。
由于不均匀系数反映的是大小不同粒组分布情况,并被用以判断级配是否良好[12],所以本文只选取级配作为风险因素,不再将不均匀系数重复作为风险因素考虑。此外,土的密度、土料相对密度、含水率、孔隙比、饱和度等都是用来描述土的三相组成,但是只要有3个独立的物理量,即可推出其他物理量。考

表1 堤防渗透失事的风险因素
虑到实验室的试验测定的方便,选取土的密度、土料相对密度及含水率作为风险因素[12]。本文综合考虑后得出堤防渗透失事的风险因素如图2所示。

图2 堤防渗透失事风险因素
渗透破坏对堤防造成的破坏最大,其发生的数量最多,分布范围广,且易诱发重大溃堤险情,是造成堤防失事的重要原因。
(3)失稳失事:失稳失事是堤防局部滑坡或整体滑坡引发的堤防溃决,分为滑坡、崩岸、跌窝等形式。相关文献[6-7,10]分析了失稳失事的风险因素。
失稳失事风险因素与渗透失事风险因素大致相同,主要区别是:在荷载因素中考虑了水位升降速率及水流淘刷;堤身堤基特性因素没有考虑渗透系数、级配和黏粒含量,而是增加了黏聚力及内摩擦角。本文综合考虑后得到堤防失稳失事的风险因素如图3所示。失稳失事作为一种常见的堤防破坏形式,失事后果严重。
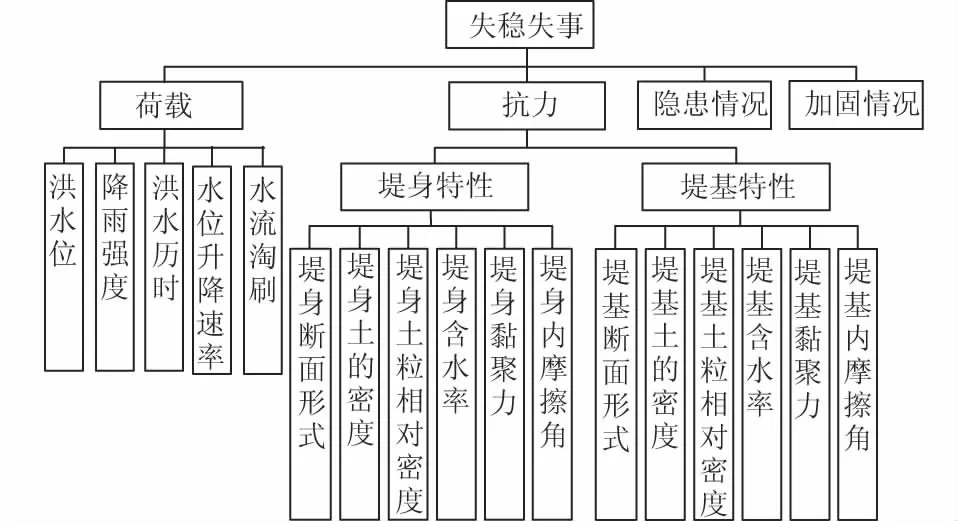
图3 堤防失稳失事风险因素
堤防安全分析中的许多风险因素具有不确定性。目前,许多学者[7,9,13-16]对风险因素的不确定性进行了研究,并给出了具有不确定性风险因素的分布形式,如表2所示。值得说明的是,土的密度、土粒相对密度等物理指标变异性较小,视为常量,仍能满足工程计算的精度要求;而黏聚力、内摩擦角等力学指标变异性较大,应该作为随机变量来处理[17]。

表2 不确定性风险因素的分布形式
进行堤防安全分析时部分风险因素之间存在互相关性,如:渗透系数与粒径大小、级配、孔隙比及饱和度有关[12];黏聚力与孔隙比、含水量及土的密度等具有较强的相关性[18];内摩擦角与孔隙比、塑性指数等有良好的线性关系[18];黏聚力与内摩擦角又存在负相关性[19]。
3 基于随机力学理论的堤防安全分析方法
在安全分析评价中使用较为广泛的方法有5种:评分法、检查表评价法、危险指数评价法、概率法和综合法[20]。可将这些方法归纳为2类:确定性方法和基于概率的不确定性方法。
堤防确定性安全分析方法将特征水位作为计算依据,对设计洪水位下某一确定洪水位工况下的典型堤防剖面进行相关计算,求得相应的安全系数,最后按照已有的规程和规范[1]进行安全性评价。然而,在进行相关计算时涉及的参量都为确定值,所以求得的安全系数并不能准确地表征堤防的安全程度,无法满足现代工程精度的要求。
基于随机力学理论的堤防安全分析方法考虑了随机因素的不确定性,由基于概率的堤防不确定性安全分析方法研究、基于随机场的堤防安全分析方法研究及考虑风险因素互相关性的堤防安全分析方法研究3部分组成。
3.1 基于概率的堤防不确定性安全分析方法
进行堤防安全性分析时,常用的概率计算方法有重现期法、一次二阶矩法、蒙特卡罗法、随机有限元法、直接积分法、梯度优化法、响应面法等。限于篇幅,本文着重综述前4种方法在堤防安全分析中的应用,并进行评价。
3.1.1 重现期法
重现期法主要用于堤防漫溢失事分析,仅考虑洪水、降雨等自然事件的随机性,并通过频率分析说明其统计特性。如Yen[21]采用传统的频率分析方法,基于古典概率理论导出n年内遭遇超标洪水的风险率计算公式,然而在复杂情况下,计算结果误差较大。
重现期法的优点是简单易行,在早期的防洪工程中有较多应用。然而,该方法是通过历史资料的统计与外延得到的,因此计算精度受限于统计资料的完备性;只考虑了水文风险因素,忽略了其他不确定的风险因素,无法准确计算整个复杂系统的风险率。
3.1.2 一次二阶矩法
一次二阶矩法或改进的一次二阶矩法可以用于堤防漫溢失事分析[14,22-23]。如,Lee和Mays[23]以曼宁方程的一次二阶矩法研究了堤防中的水力不确定性,结果表明糙率和摩擦阻力是水力不确定性的重要影响因素,二者约占水力不确定性95%。梁在潮和李泰来[14]给出了堤防防洪能力影响因素的统计及计算方法,采用改进的一次二阶矩法计算了某堤防防洪能力的风险率。
朱勇华等[24]将一次二阶矩法用于堤防渗透失事分析中,建立了不透水堤基均质土堤、透水堤基均质土堤和双层地基均质土堤渗透破坏风险率模型。
一次二阶矩法或当量正态化法(JC法)也可以用于堤防失稳失事分析[25-27]。如,姚耀武和陈东伟[25]建立了土坡稳定可靠度分析的极限状态方程,并与通用的JC法可靠度分析程序结合起来,可用于考虑随机变量的非正态分布、相关性和有截尾要求的工程土坡稳定分析中。周建普等[26]将定值分析法与一次二阶矩法相结合,计算土坡的可靠度指标,并探讨了土体参数的变异性、安全系数变异性和可靠性指标之间的内在联系。
一次二阶矩法计算简单,使用方便。但对于非线性程度较高的功能函数会导致计算结果与精确解相差过大;同时,该方法需要复杂土体随机参数的统计资料,所以将该方法应用于堤防工程失事分析中仍存在诸多难题。
3.1.3 蒙特卡罗法
蒙特卡罗(Monte-Carlo,MC)法又称随机抽样法,其通过对随机变量的大量抽样及对抽样结果的统计分析,将结构失效次数占总抽样次数的频率记为结构的风险率。
董胜和王腾[28]将蒙特卡罗法用于堤防漫溢失事分析中,通过蒙特卡罗法模拟产生洪水系列,提出采用重点抽样法进行防洪工程风险率计算,同时考虑了随机变量间相关性大小对风险率的影响,并对有关参数进行了灵敏度分析。
蒙特卡罗法也可以用于堤防渗透失事和失稳失事分析中[5,29-31]。如,王卓甫等[5]主要考虑了土体物理力学性能指标的不确定性,使用蒙特卡罗法计算了防洪堤岸坡滑动失稳的风险率。张俊芝和邹传仁[29]在建立了边坡失稳基本计算模型的基础上,利用矩阵语言程序结合蒙特卡罗法编制了寻找最危险滑动面的程序,实现了边坡稳定最大失效概率的计算。吴兴征和赵进勇[31]通过使用蒙特卡罗法求解失稳概率,建立了基于可靠性理论的边坡稳定和渗透稳定风险评价模型,此模型已应用于长江干堤部分堤段的风险评价系统中。
蒙特卡罗法不受极限状态函数复杂程度的影响,也不需要将状态函数线性化和随机变量等效正态化,其模拟计算的收敛速度与基本随机向量的维数无关。蒙特卡罗法抽样数量较多时,可以达到非常高的计算精度,可用于校核其他近似分析方法的计算结果,是预测和估算可靠度常用的方法之一。蒙特卡罗法的缺点是计算次数多,耗时长。
3.1.4 随机有限元法
随机有限元法(Stochastic Finite Element Method,SFEM)是在传统有限元的基础上发展起来的一种工程数值计算方法,主要包括随机变分原理、建立随机有限元控制方程及其求解3部分。
李锦辉[32]将随机有限元法用于堤防渗透失事分析中,推导了三维稳定渗流的随机变分原理和相应的有限元列式,使用Taylor展开随机有限元方法,对堤防渗透稳定问题进行风险分析,并将研究成果应用于南京秦淮河武夷绿洲段堤防。
李典庆等[33-34]将随机有限元法用于堤防失稳失事分析中,提出了考虑土体参数空间变异性的边坡可靠度分析的非侵入式随机有限元法,并开发了非侵入式岩土工程概率分析软件NIGPA。随后又提出了基于子集模拟的边坡风险评估的高效随机有限元法,推导了基于子集模拟的边坡失效概率的计算公式,并给出了基于高效随机有限元法的边坡可靠度分析方法和风险评估流程图。
随机有限元法是用随机变量、随机过程或随机场来描绘堤防工程中的风险因素,更接近于工程实际问题。此方法是对随机结构进行分析并估算结构强度可靠度的强有力工具,具有广阔的应用前景。不过该方法在应用方面还远不如确定性有限元法那样普遍,主要应用于静力分析和随机特征问题,对随机结构的动力响应分析仍处于研究之中。
3.2 基于随机场的堤防安全分析方法
基于随机力学的堤防安全分析中,分析对象即随机因素可分为随机变量、随机过程、随机场及随机过程和随机场的结合[35]。在3.1节中,诸多研究把相同土层土体参数仅仅当作纯随机的随机变量来处理,无法反映空间局部范围和特定方向上的变化特征和规律,即只是考虑了土体参数的点变异性,不能对其空间变异性和自相关性作出更准确的评价。Vanmarcke[36]将随机场理论应用于岩土工程,首次提出了土层剖面的随机场模型,其实质是用齐次正态随机场来模拟土层剖面,用方差折减系数将点的变异性和空间变异性联系起来,能更准确地描述土体参数的空间变异性和自相关性。目前,基于随机场的堤防安全分析方法的研究主要包括随机场的相关距离求解、随机场的离散方法及随机场与有限元法的结合。
3.2.1 随机场的相关距离求解
Vanmarcke[36]提出了相关距离是描述随机场特征的重要参数,是衡量2个相隔一定距离的物理量之间的相关程度的基本距离,相隔间距小于此距离的2点之间的物理量被认为是相关性较强的,反之则可认为是不相关的。相关距离的计算方法有递推空间法、相关函数法、曲率极限法等[37-38]。程强等[37,39]通过计算300余个土层的土体参数相关距离,对相关函数法、相关函数模型选择、拟合范围等问题进行了分析探讨。闫澍旺等[40]对递推空间法和相关函数法进行比较,从理论上证明当样本容量足够大时,2种方法的计算结果可以统一;对相关函数法作出改进,使其更易于曲线的拟合和参数的确定。冷伍明和赵善锐[38]通过研究土体随机场理论,就相关距离的计算提出了曲线极限法。
3.2.2 随机场的离散方法
随机场的离散方法主要有中心点法、局部平均法、加权积分法、正交级数展开法等[41]。Vanmarcke[42]首先提出了随机场离散的局部平均法,该方法将随机场在每个单元的属性用随机场在单元上的局部平均来表征。安利强等[43]给出了矩形单元和任意四边形单元局部平均随机场的二阶统计特性的计算方法,并以一平稳随机场为例,分析了相关函数、相关尺度及高斯积分点对局部平均单元协方差矩阵的影响。李永见等[44]采用局部平均法对三维土性参数随机场进行离散。Zhang和Ellingwood[45]提出了正交级数展开法,通过选择完备的正交函数系列来避免直接求解积分方程特征值问题。
3.2.3 随机场与有限元法的结合
Hisada和Nakagiri[46]在随机有限单元离散中考虑了随机场因素,采用摄动法来计算反应量的二阶矩。Deodatis[47]将随机有限元的摄动法展开式和随机场的加权积分法结合,提出了变异响应函数的新概念。朱位秋和任永坚[48]在各有限单元上使用局部平均法离散随机场,建立了局部平均的一阶、二阶统计量与原向量随机场的一阶、二阶统计量之间的关系,导出了用有限元法计算含多个相关随机参数的结构在随机静载荷作用下的位移与应力的一阶、二阶统计量的公式。王飞等[49]在随机有限元计算中,将渗透系数视为三维独立正交随机场,利用可分离向量的局部平局法进行随机场的离散。程演[50]采用随机场模型描述天然土体的空间变异性,将蒙特卡罗(MC)法和有限元法相结合,建立了随机空间变异非饱和土体渗流变形模型,并进行有限元计算分析。杨杰等[51]采用基于Cholesky离散方法的蒙特卡罗随机有限元法,实现考虑堆石料力学参数变异性的随机有限元计算,从而构造相关向量机(RVM)的学习样本;进而通过先进的机器学习算法-RVM建立反分析模型中输入-输出间的不确定性关系,有效模拟材料参数与坝体沉降间的复杂非线性关系,使其能够代替随机有限元进行计算。
3.3 考虑风险因素互相关性的堤防安全分析方法
堤防安全分析中部分风险因素存在互相关性,然而现在的堤防风险率或可靠度计算中,绝大多数都是将风险因素作为独立标准正态变量考虑,没有考虑输入随机变量的互相关性或只考虑了输入随机变量为线性关系的简单情形。因此,为了能更加合理地对堤防进行安全分析,实现对其安全性较为准确的评价,非常有必要加强对风险因素间互相关性的研究。目前相关研究主要体现在以下方面。
3.3.1 风险因素互相关性的确定和影响
许多学者[12,18-19]对此进行了研究,并取得了一定进展。如:范明桥和盛金宝[19]着重对土体强度抗剪指标黏聚力c和内摩擦角φ的相关性及其对可靠性分析的影响作了研究,结果表明c和φ之间存在着较强的负相关性,对土工构筑物的可靠度影响很大,不考虑c和φ相关性的土工构筑物可靠度评估结果是偏低的。
3.3.2 考虑风险因素互相关性的分析方法
该分析方法主要有广义随机空间分析法、Orthogonal变换、Rosenblatt变换、Nataf变换等[52]。赵国藩和王恒栋[53]把随机变量和广义随机空间联系起来,建议在广义随机空间内进行可靠度分析,能够有效地考虑随机变量的互相关性。吴帅兵等[54-55]介绍了将相关非正态变量转化为独立标准正态变量的3种变换方法:Orthogonal 变换、Rosenblatt 变换及Nataf变换,并采用算例详细地比较了这3种变换方法对可靠度结果的影响、优缺点及适用范围。陈雁等[56]提出基于拉丁超立方采样的蒙特卡罗模拟概率(Correlation Latin hypercube sampling Monte-Carlo Simulation,CLMCS)潮流计算方法,可以处理多个输入随机变量的互相关性,具有不受输入随机变量概率分布类型的约束、精度高、速度快等优点。唐小松[57]提出了基于Copula函数的岩土参数联合概率分布模型构建方法,建立了有限数据条件下互相关非正态岩土体参数二维和多维分布模型。姜潮等[58]提出了一种考虑变量之间相关性的概率-区间混合不确定性模型:通过引入相关角的概念,定量描述任意2个变量之间的相关性;通过仿射坐标,将相关变量转化为独立变量。
3.3.3 风险因素互相关性分析方法的工程应用
姚若军[59]采用协方差矩阵转换法,解决了土坡可靠度计算时土性参数存在互相关性的问题。周泽华[60]在进行边坡可靠度分析时,利用A-D检验对单个土体参数的概率分布分别进行了研究,同时采用Copula函数建立土体参数的联合概率分布,准确描述各土体参数间的互相关性。
4 结 语
基于随机力学理论的堤防安全分析方法考虑了风险因素的不确定性,属于不确定性安全分析方法。在基于概率的堤防不确定性安全分析方法研究中,把风险因素看成随机变量,使用一次二阶矩法、蒙特卡罗法、随机有限元法等,计算堤防工程的风险率或可靠度。
在基于随机场的堤防安全分析方法研究中,引入随机场理论,用随机场模型代替随机变量模型来描述土体参数。目前,该领域的研究重点是随机场的相关距离求解、随机场的离散方法及将随机场模型与有限元方法结合,前景较为广大,但仍存在随机场与有限单元耦合等诸多实际问题。
在考虑风险因素互相关性的堤防安全分析方法研究中,对风险因素间互相关性的确定及其对可靠度影响的研究已经取得一定进展,但由于风险因素众多,数据资料匮乏且收集不易,仍需进一步研究。此外,对处理风险因素间互相关性的方法也进行了深入研究,这些方法有基于拉丁超立方采样的蒙特卡罗模拟概率(CLMCS)潮流计算方法、Nataf变换法、基于Coupla函数描述互相关性方法等。这些方法在边坡稳定性分析、管道可靠度计算等方面已经有了相关应用,因此可以考虑将上述理论方法引入到堤防安全分析中来,用于解决渗透分析与失稳分析中部分参数存在互相关性的问题,进一步完善堤防安全分析方法。

