小样本结构参数不确定性量化及传递分析的信息扩散方法

骆勇鹏，鲁四平，刘景良

（1.福建农林大学 交通与土木工程学院，福州350108；2.中南大学 土木工程学院，长沙410075）

实际工程结构在制造、加工、装配、建模等环节中不可避免地存在各种不确定性因素，如制造误差及载荷不确定性等，使得结构性能也表现出一定的变异特性。若在结构分析时忽略这些不确定性因素的影响，采用确定性模型和确定性方法进行分析，可能出现理论分析和实际结构响应不吻合等问题，对结构的安全分析和设计产生不可忽略的影响[1-3]。

当样本充足时，概率模型是对不确定性进行度量的一种有效办法[4]。此时，不确定性通过具有某种分布形式的随机变量或随机过程来量化，并以此开展结构的不确定性传递分析[5]。目前该方面的研究已取得一定的成果。Doebling 等[6]提出了基于蒙特卡罗和有限元分析的不确定性正向传递计算方法。徐腾飞等[7]利用蒙特卡罗与钢筋混凝土非线性有限元法，研究钢筋混凝土梁在服役期间变形随机性的变化规律。该分析过程每次加载的非线性分析次数为10 000 次，计算成本较大。为了弥补蒙特卡罗有限元分析方法的不足，宗周红等[8]提出一种基于响应面模型的蒙特卡罗模拟，并将其应用到下白石大桥的不确定性分析和量化中，在保证模型精度的前提下提高计算效率。

值得注意的是，实际工程中因条件限制往往不能获取足够的样本数据来估计随机变量的概率密度函数。现有研究成果只能通过假定不确定性参数的概率密度函数，进而开展不确定性传递分析。也有学者提出通过拟合优度检验（如K-S检验）等方法来估计不确定性参数的概率分布[9]。在样本个数较多的情况下，该方法是可行的。但是当样本数量较少时，所确定的概率分布本身具有一定的不确定性[10]，甚至可能出现假定的概率密度函数与实际不符的情况，此时将产生较大的误差，进而影响结构实际服役性能评价。

因此可以说不确定性分析和设计结果的准确性与真实性很大程度上依赖于不确定性源的量化。概率密度函数的选取对不确定性分析结果有较大影响，受工程实际可获取信息的局限，如何基于有限样本对不确定性参数进行量化及传递分析是当前的发展重点[4]。信息扩散理论通过将单值样本转换成概率形式表达的模糊集值样本，进而对非完备样本信息进行有效处理[11]，可在一定程度上解决结构不确定分析中概率分布难以确定的问题，目前已逐步应用于测绘工程、灾害评估、岩土工程等领域。本文将其引入到不确定性量化和传递分析中，提出新的不确定性参数量化和不确定性传递分析方法，以数值算例和试验钢板模态频率不确定性分析为例，验证所提方法的可行性及可靠性。

1 基于信息扩散的不确定性参数量化及传递分析

1.1 不确定性参数概率密度函数估计

信息扩散原理的基本思想为：设X是不确定性参数的已知观测样本。li为Xi的观测值。若X是非完备的，则存在扩散函数μ(x)，使得li所获得的量值为1 的信息可根据μ(x)的量值扩散，且扩散得到的原始信息分布能够更好地反映总体规律[11]。

根据上述原理对母体的概率密度函数进行估计的过程称为扩散估计，其定义如下：

设μ(x)为定义在[-∞,+∞] 上的一个Borel可测函数则称

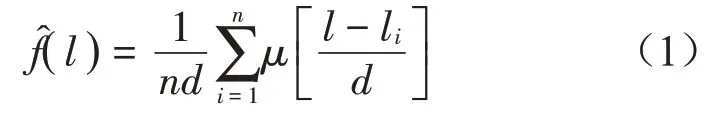
由式（1）可知，要对不确定性参数的概率密度函数进行估计，首先要确定扩散函数μ(x)和窗宽d[11]。黄崇福提出了基于分子扩散理论的正态扩散函数和基于择近原则的经验窗宽确定方法[11]。但是该方法不适用于所有分布（如非对称和非正态分布），且根据不同窗宽计算得到的母体概率密度函数的估计精度是不同的[12]。

为了提高母体概率密度函数的估计精度及扩大其适用范围，王新洲等提出可在母体概率密度函数估计的均方误差最小准则求得最优窗宽。而在确定最优窗宽前要先确定最优扩散函数。同样根据均方误差最小准则，王新洲等推导出了最优扩散函数的形式[13]。研究表明采用最优窗宽估计母体概率密度函数，其精度比经验窗宽估计母体概率密度函数要高很多，并且其曲线能很好地逼近理论分布曲线[13]。为此，本文也采用最优窗宽和最优扩散函数来获得不确定性函数的概率密度函数。

根据文献[13]中的推导，使母体概率密度函数估计的均方误差最小的最优扩散函数的形式为

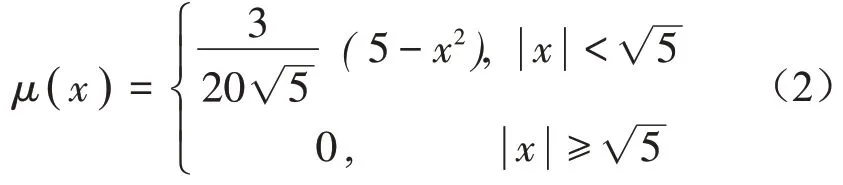
最优窗宽的迭代公式

第三，创新知识体系。要建立独立学院法学专业新的教材体系，它既不是普通本科教材的浓缩，更不是删减，而是知识体系的创新。新教材体系要以专业人才培养目标为依据，全面提高人才培养素质和教育教学质量，系统地研究、借鉴传统法学教材的优点，创立新的体例和新的语言风格，既要照顾到法律基础理论，又要突出实用性。

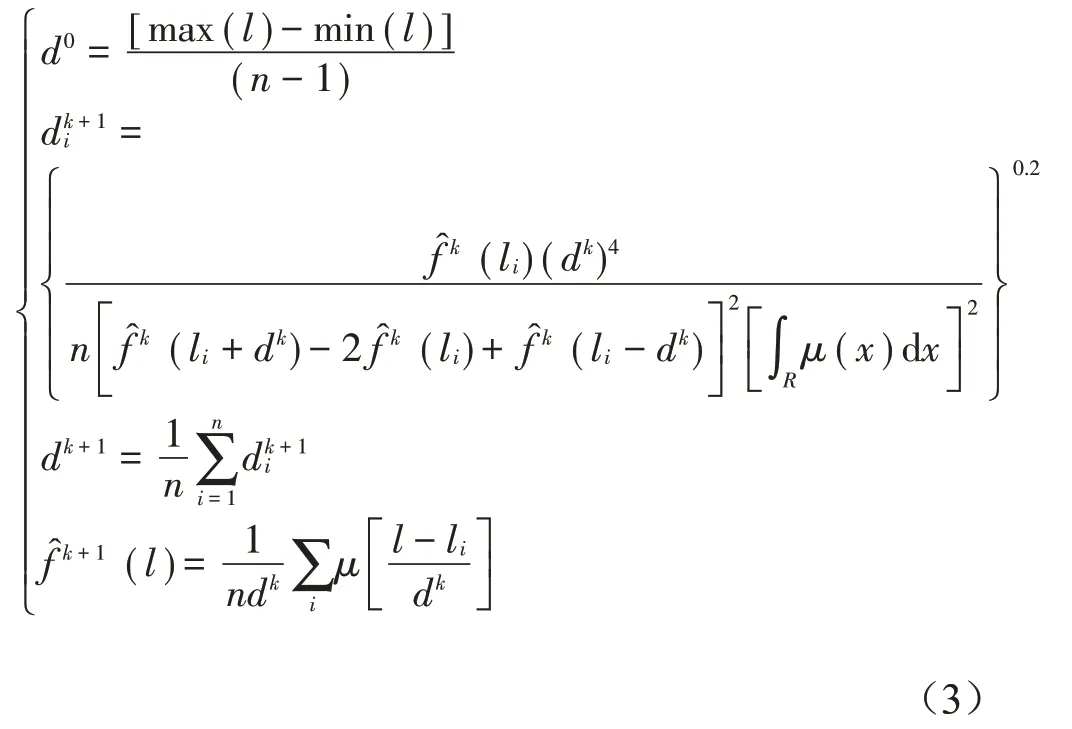
1.2 随机数生成及参数不确定性量化

考虑到估计的概率密度函数不是常规的概率密度函数，如何生成符合该概率密度函数的随机数也是一个值得考虑的问题。本文引入接受-拒绝法[14]进行伪随机数的生成。按照估计的概率密度函数对均匀分布序列的随机数序列进行舍选。该步骤的具体实现过程[15]为：

首先选择g(l)作为建议分布的概率密度函数，然后确定一个常数M＞1，使得在l的定义域上均有成立；然后生成服从概率密度函数为g(l)的建议随机数y和一个服从均匀分布U(0,1)的随机数u。最后，计算接收准则的概率函数h(l)=，如果u＜h(y)，则接收所生成的随机数y；反之，则丢弃该随机数y，重新进行随机数生成。

通过以上步骤可以生成符合不确定性参数概率密度函数的随机样本数据，根据式（4）和式（5）计算不确定性参数的均值和标准差，达到量化结构参数不确定性的目的。

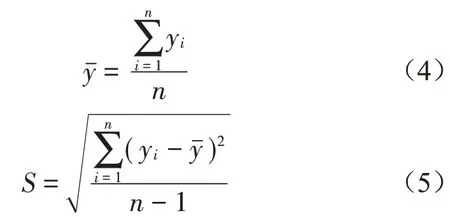
采用接受-拒绝法进行随机数生成时，首先要选择常用分布的概率密度函数作为建议概率密度函数，保证g(l)容易被抽样（本文以均匀分布的概率密度函数作为建议概率密度函数）。其次Mg(l)要能够完全罩住，且形状尽量与相似，这样可以提高抽样的效率[15]。

1.3 不确定性传递分析

为快速计算参数不确定对结构响应的影响，基于逐步回归分析理论，建立反映参数与响应之间的复杂关系的不完全二次多项式响应面模型[16]，如式（6）所示。

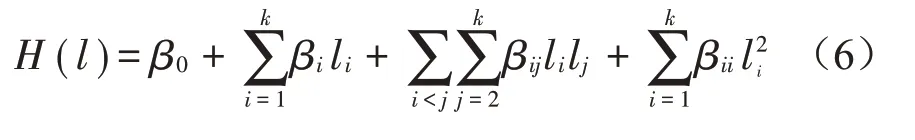
式中：li∈[lli,lui]，lli、lui是参数的取值范围；β0、βi、βij、βii是回归系数。

将随机样本代入响应面中快速计算随机样本对应的结构响应，经统计分析可得响应的均值和标准差，从而估计多个参数变异对结构动力响应变化的影响。

图1为所提的小样本结构参数不确定性量化及传递分析的信息扩散方法的计算流程。

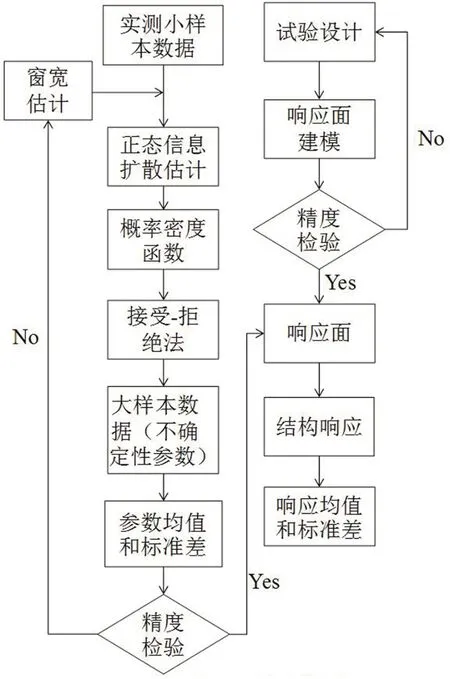
图1 所提方法计算流程图

2 数值算例

以4自由度质量-弹簧系统（如图2所示）来验证所提方法的有效性。首先假设系统的不确定性均来源于刚度参数的不确定性。其中k1和k2真实值服从均值为1，标准差为0.1的正态分布，其余参数真实值设置为

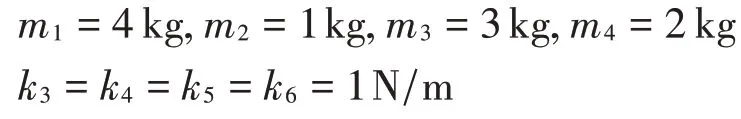
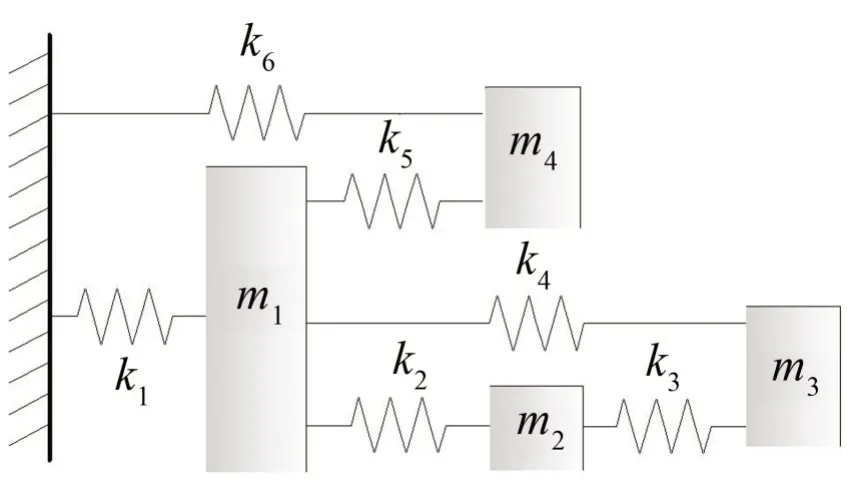
图2 4自由度质量-弹簧系统

2.1 参数不确定性量化

以k1参数为量化对象，根据k1所服从的概率分布函数，分别随机抽取200 个数据作为真实不确定性参数的测量数据，其中均值为0.992 9，标准差为0.098 3。分别从200 个数据中抽取前5 个、10 个、15个、20个和25个数据作为小样本实测数据。基于提出的量化方法对刚度参数k1进行量化，均值和标准差的估计结果如表1所示。

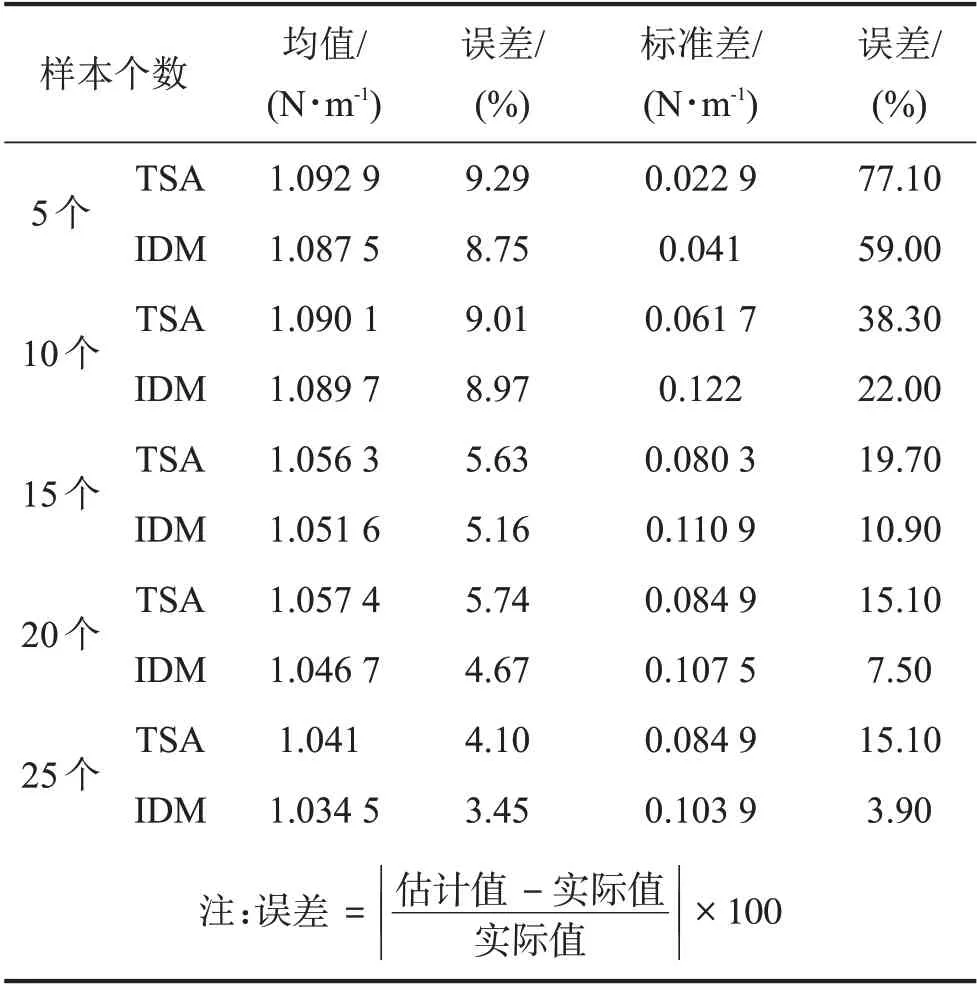
表1 k1参数量化结果分析

表1同时给出直接基于5 个、10 个、15 个、20 个和25 个k1数据计算得到的均值和标准差。为了便于描述，将所提的基于信息扩散的参数不确定性量化方法简称为IDM（Information Diffuse Method）；将直接对小样本数据进行统计分析的方法简称为TSA（Traditional Statistical Analysis）。由表1可知，通过IDM 计算得到的均值和标准差相较于TSA 更接近于模拟实测变量的取值情况，尤其是标准差的误差精度得到显著提高。如图3所示。

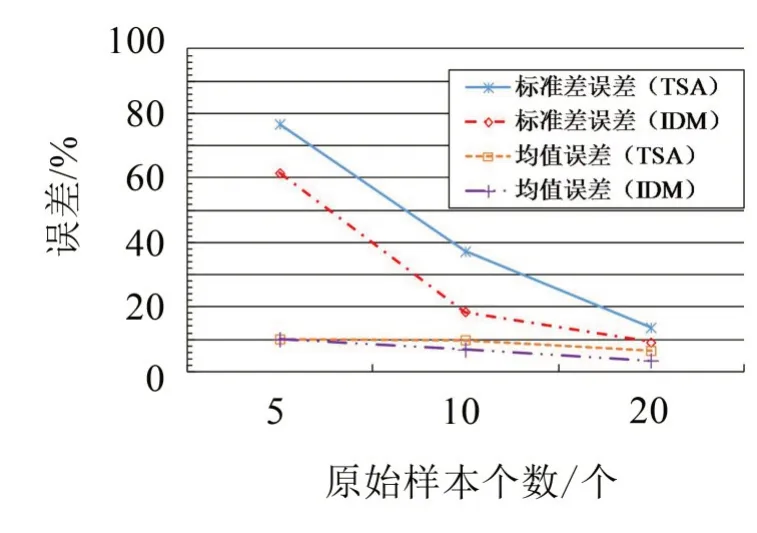
图3 预测和实际概率统计特征值的误差

从图3可知，IDM 和模拟实测值的误差随着样本点个数的增加而减小，当样本个数为20 个时，均值和标准差的误差分别为4.67%和7.5%，满足工程精度要求。参数k2的量化过程及结果与参数k1类似，限于篇幅，不再赘述。

2.2 不确定性传递分析

以20 个数据作为小样本实测数据，分别根据k1和k2的量化结果，计算2 个刚度参数不确定性对质量-弹簧系统的前4 阶模态频率的影响，结果如表2所示。

从表2可知，采用所提的不确定性方法及传递分析计算得到的前4阶模态频率均值与模拟实测模态频率均值吻合良好，最大误差为2.46%。前4 阶模态频率标准差与模拟实测模态频率标准差最大误差为-14.88%。从图4和图5可知，预测频率和模拟实测频率的分布范围较为接近，验证了所提方法的可行性及可靠性。

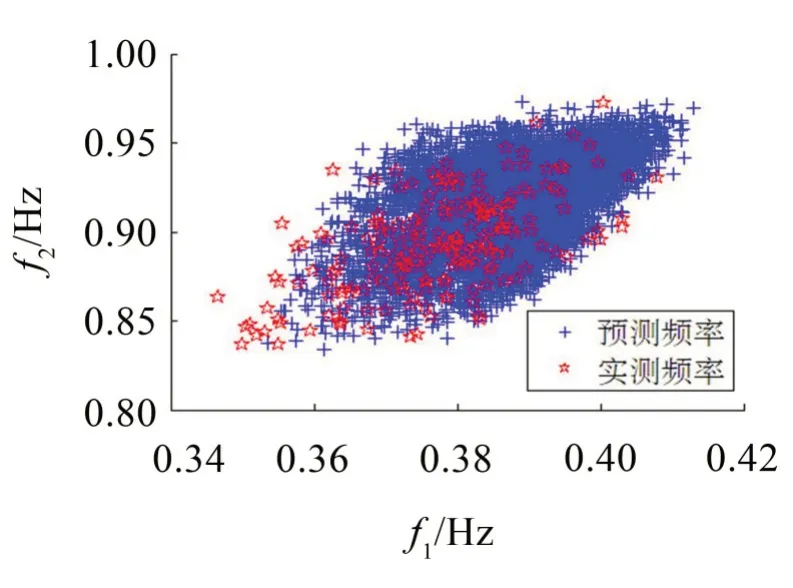
图4 预测和模拟实测的第1阶、2阶模态频率散点图

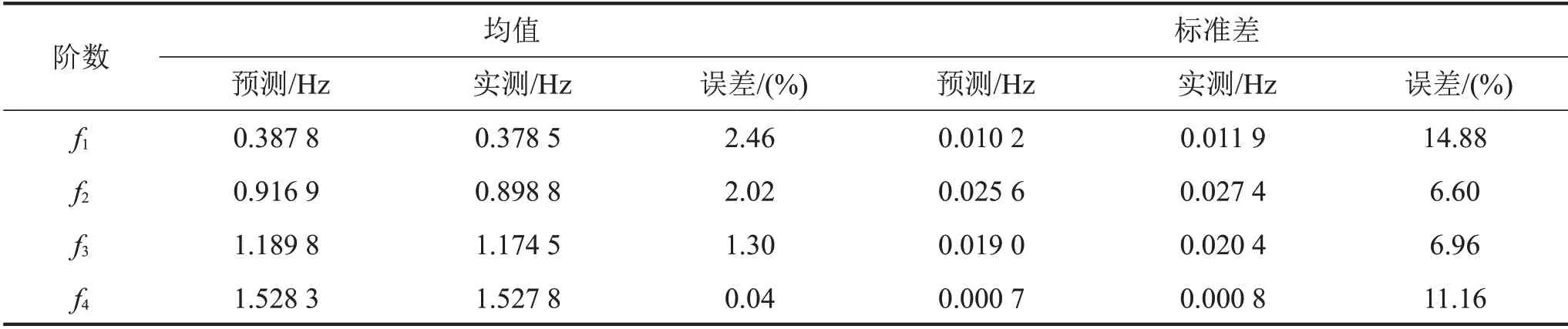
表2 预测频率与实测模态频率概率统计特征值

表3 频率实测值的统计特征值[17]

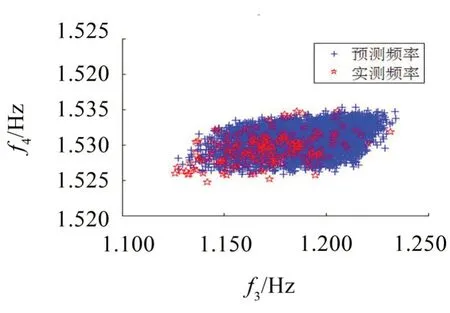
图5 预测和模拟实测的第3阶、4阶模态频率散点图

3 试验钢板频率响应不确定性分析

以33 块具有相同名义尺寸及材料参数的钢板为研究对象[17]，在自由边界条件下，采用锤击法对33块钢板进行模态试验，得到33 块钢板的前5 阶模态频率值及其统计值，如表3所示。

钢板模态试验示意图如图6所示。

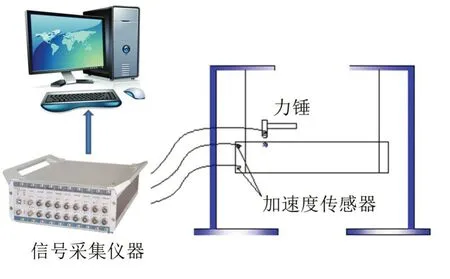
图6 钢板模态试验示意图

3.1 材料参数不确定性量化

该组钢板的名义尺寸为564 mm×110 mm×1.45 mm，弹性模量、剪切模量、质量密度的名义取值分别为210 GPa、83 GPa 及7 860 kg/m3。在不考虑测量误差影响的前提下，文献[17]采用随机模型修正方法对钢板的弹性模量E和剪切模量G的均值和标准差进行了估计，结果如表4和表5所示。本文根据随机模型修正预测的材料参数均值和标准差，假定其服从正态分布，分别随机抽取20个钢板弹性模量和剪切模量值作为模拟实测值。

基于20个样本，采用所提方法对钢板材料参数不确定性进行量化。表4和表5给出了均值和标准差的量化结果。

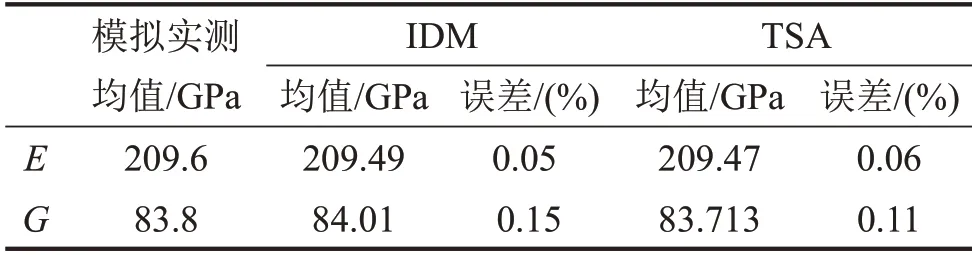
表4 预测及模拟实测参数均值

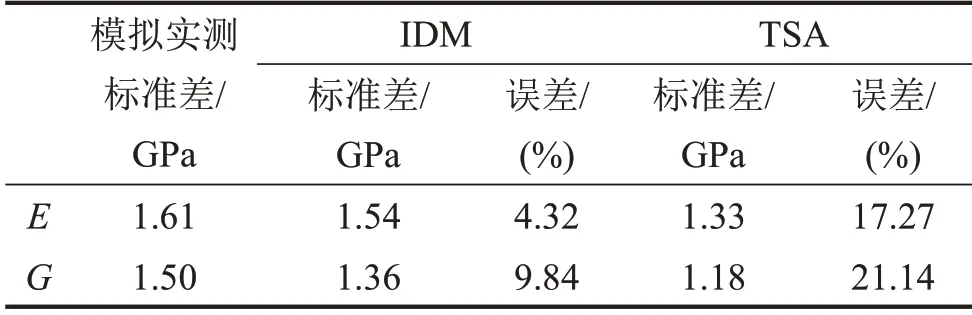
表5 预测及模拟实测参数标准差

从表4和表5可知所提方法估计的均值误差最大为0.15%，标准差误差最大为9.84%，相较于TSA的计算结果而言，有较大改善，特别是标准差的估计精度上，有明显改变，说明所提方法在小样本的情况下可以有效地估计总体的均值和标准差。

3.2 不确定性传递分析

为了快速计算材料参数不确定性引起的钢板前5阶模态频率的变异程度，采用中心复合设计确定试验点，结合逐步回归分析方法，得到前5阶模态频率的响应面模型，其中第1 阶模态频率响应面模型如式（7）所示。

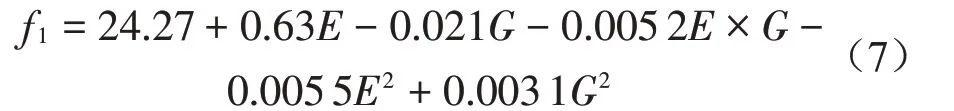
根据不确定性参数量化结果，随机抽取2 000个样本点代入各阶响应面模型中，快速计算前5 阶模态频率值并进行概率统计分析，结果如表6所示。

从表6可知，前5 阶模态频率均值最大误差为1.23%，标准差最大误差为15.88%，满足工程精度要求。从图7可知，实测模态频率大部分在随机抽样范围里面，预测模态频率和实测模态频率的分布基本吻合，进一步说明前述材料参数不确定性量化结果的准确性。

4 结语

本文在不确定性分析中引入信息扩散理论，提出基于信息扩散理论的小样本结构参数不确定性量化及传递分析方法。质量-弹簧系统数值模拟算例和钢板试验表明不确定性参数估计精度随着样本点个数的增加而增加，当样本个数为20个时可得到较好的估计结果，在一定程度上解决了小样本参数概率密度函数难以确定而导致参数不确定性量化困难的问题。

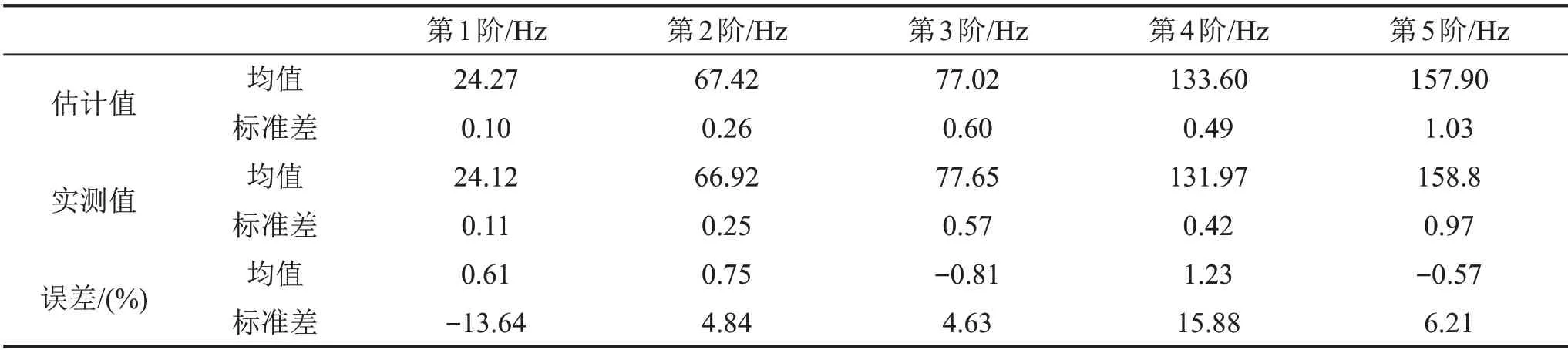
表6 频率实测值及统计值

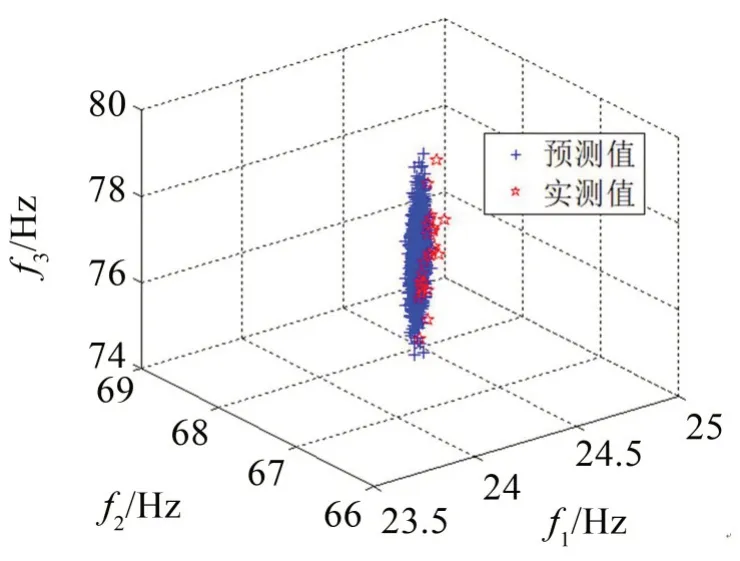
图7 预测和实测的第1－3阶模态频率散点图