与黏弹性地基相互作用的单桩的自振特性分析

柳 伟，张斌伟，柳德龙

（1.兰州新区城市发展投资集团有限公司，兰州730087；2.陇东学院 土木工程学院，甘肃 庆阳745000；3.甘肃省高校“黄土工程性质及工程应用”省级重点实验室，甘肃 庆阳745000；4.中国铁路乌鲁木齐局集团有限公司，乌鲁木齐830011）

桩基作为众多工程领域中的一种深基础结构形式，以其简单、适用而广泛应用于铁路、公路、机场、海洋平台、高层建筑地基基础等，其振动特性一直在科学以及工程应用中备受关注[1-3]。

土与结构相互作用下这一问题的复杂性，历来都是岩土工程、结构工程、固体力学接触问题中的棘手难题。蒲育、滕兆春[4]基于Hamilton 原理和线弹性理论，应用微分求积法研究弹性地基梁自由振动的无量纲频率特性，但没有考虑实际工程中土体阻尼的影响。张阿舟[5]在考虑桩周土刚度及阻尼的情况下采用分离变量法求解了全埋置一维桩的自振频率及振型，若运用该方法在求解二维埋置结构自振特性时，得到的频率方程以超越方程形式表达，计算会更加复杂。彭丽等[6-7]采用复模态方法分析了黏弹性三参数地基上梁的横向振动特性，并用微分求积方法加以验证，但没有分析衰减系数对自振特性的影响。陈兴冲[8]采用瑞利法推导计算浅平基桥墩、桩基桥墩及沉井基础桥墩基频的近似公式，但该方法不易推广至高阶自振频率的计算。杨骁等[9]将桩等效为Reyleigh 梁，利用精确有限元法求解成层液化土单桩-土-结构系统的固有频率，但运用该方法求解Timoshenko梁理论模型时，它的形函数不再精确，必须以增加结构单元数量为代价提高计算精度，不易推广至现实的工程中去，而波动理论对以上问题的解决提供了一条有效的途径。

回传射线矩阵自1998年首次引入结构计算以来，已被成功应用于框架结构及各向同性层状介质的瞬态响应及振动分析[10-13]，其物理意义明确、列式统一、易于编程，且具有高精度、低耗时、结果可读性强等优点，在结构动力学分析中具有独特的优势。截止目前，对黏弹性地基中结构自振特性的相关研究工作还很少。

本文将回传射线矩阵法推广至桩土系统的振动分析中，运用回传射线矩阵法及求根法，利用MATLAB语言编程，通过具体算例，分析了外露长度、埋置深度、桩端约束情况对埋置结构自振特性的影响，所得结论不仅对结构的质量检测具有指导意义及工程应用价值，而且可以为结构设计和施工计算提供理论基础。

1 回传射线法及求根法的基本原理

本文基于Timoshenko 梁理论的Winkler 地基模型，将桩基划分为2 个单元3 个节点，节点的编号如图1（a），建立整体坐标系(X,Y)，引入2 个对偶局部坐标系(x,y)JK和(x,y)KJ，如图1（b）所示。

在局部坐标系下，12、23单元的波动控制方程为

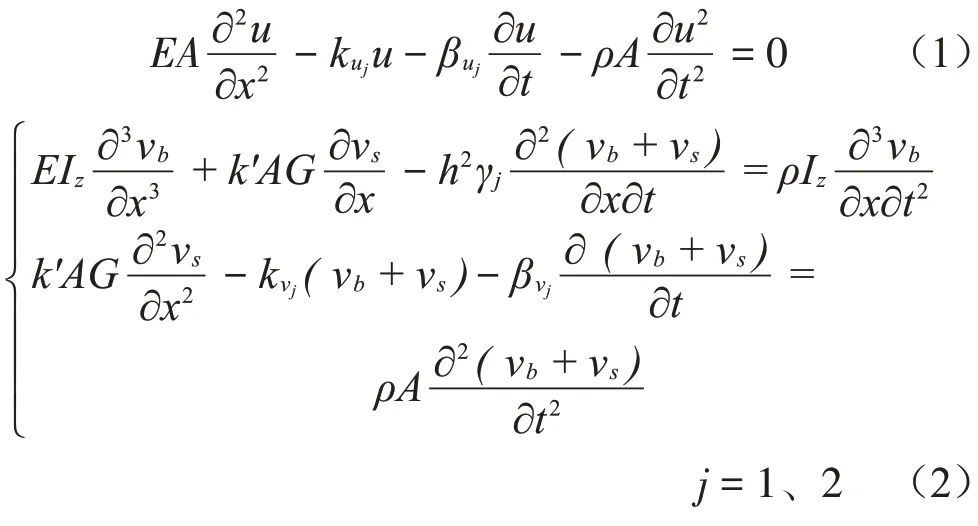
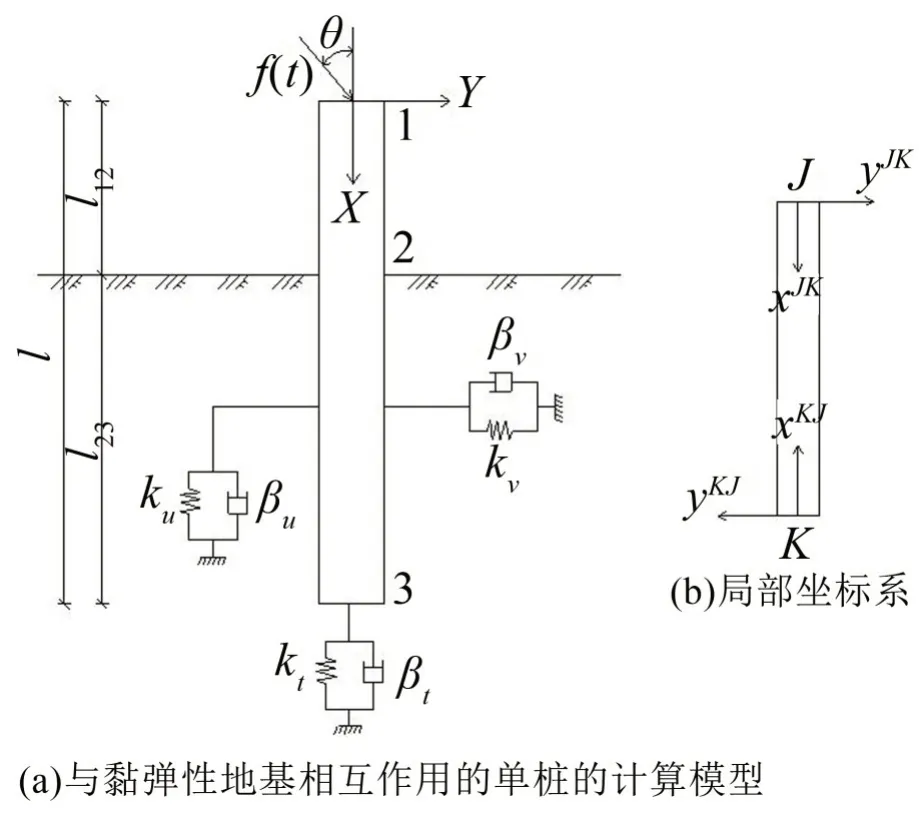
图1 与黏弹性地基相互作用单桩的计算模型及局部坐标系

式中：u(x,t)为轴向位移；vb(x,t)为弯矩引起的挠度，vs(x,t)为剪力引起的挠度；l、l12、l23分别为单桩的总长、外露长度、埋置长度；E、G、ρ、h、A、k'、Iz分别为单桩的弹性模量、剪切模量、密度、横截面高度、横截面面积、截面剪切系数、横截面惯性矩；kuj、kvj、βuj、βvj、γj分别为土体纵向弹簧系数、土体横向弹簧系数、土体纵向阻尼系数、土体横向阻尼系数和桩身截面转动时的土体摩擦阻尼系数；j=1 时，ku1=βu1=kv1=βu1=γ1=0；j=2 时，ku2=ku，kv2=kv，βu2=βu，βv2=βv，γ2=γ。

将式（1）式（2）直接进行Fourier变换并整理得

求解式（3）－式（4）得位移在频域中的表达式为

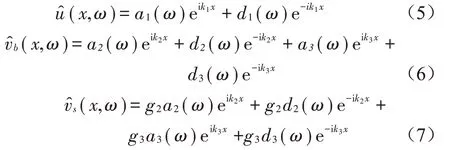
式中：a1(ω)、a2(ω)、a3(ω)为待定的入射波波幅；d1(ω)、d2(ω)、d3(ω)为待定的出射波波幅；k1、k2、k3为波数，满足

式中：j=1 时，k11(ω)、k21(ω)、k31(ω)对应12 单元的波数；当j=2 时，k12(ω)、k22(ω)、k32(ω)对应23 单元的波数；

对应于波数k2j,3j与的比值为

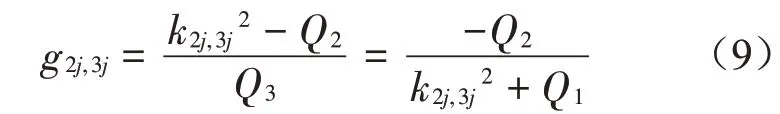
轴力、弯矩、剪力和转角在频域中的表达式为

如图2所示的受力分析图，对节点1建立力平衡和位移协调条件

根据图3所示的受力分析图，对节点2建立力平衡和位移协调条件。

图2 节点1受力分析图

图3 节点2受力分析图

根据图4所示的受力分析图，对节点3建立力平衡和位移协调条件

图4 节点3受力分析图

将式（10）－式（13）代入式（14）－式（16），并将局部坐标系下的矩阵形式组集成整体坐标系下的矩阵形式为

式中：d、a为总体出射波和入射波波幅向量；S、s为整体散射矩阵和整体源矢量。

从局部坐标系的角度看，对于任一个单元JK，其中一端的入射波对另一端而言就是出射波，因此，入射波的波幅向量和出射波的波幅向量满足以下相位关系

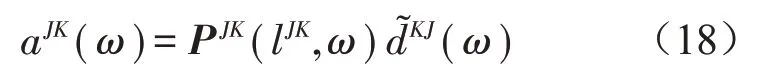
式中：aJK(ω)和dJK(ω)为同一个单元两个节点处的入射波波幅和出射波波幅；PJK(lJK,ω)称为传播矩阵表示单元JK的长度。

将所有杆件单元的入射波波幅向量aJK(ω)和出射波波幅向量(ω)组集到总体入射波波幅向量a和总体出射波波幅向量d～中，写成紧凑形式为

由于～与d中各元素相同，而排列顺序有所变化，因此，引入置换矩阵U，以调节～中各元素在总体坐标系中的相对位置，有

将式（20）代入式（17），得

式中：R=SPU为回传射线矩阵；I为单位矩阵。

黏弹性地基中桩基自由振动时，其波源矩阵s=0，即

式中：d(ω) 有非零解的条件为系数行列式|I-R(ω) |必须为零，由于结构在黏弹性地基中自由振动时需考虑土体阻尼对振动的衰减作用，令圆频率ωn=+iδn。其中，实部为所求的自振频率，虚部δn为对应的衰减系数。

由于R(ω)中的各项是关于自振频率ωˉn及衰减系数δn的二维复数超越方程。在数学上此类问题只有数值解而没有解析解。考虑到以上因素，根据回传射线矩阵法的列式特点提出将二分法和黄金分割法(简称求根法)结合起来进行迭代求解复杂复数方程，即：分别对ωn的实部和虚部δn进行循环，当[I-R(ω) ]的模小于预先给定的误差时，取出对应的ωn，则ωn的实部ωˉn为所求的自振频率，虚部δn为对应的衰减系数。

求得结构的自振频率及衰减系数后即可求得自由振动时的振型曲线，由线性代数的知识可知，矩阵与其行列式的值有如下关系

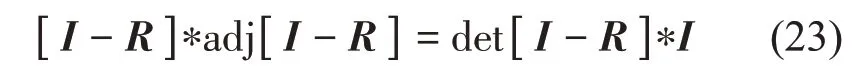
式中：adj[I-R]为矩阵[I-R]的伴随矩阵；det[I-R]为矩阵[I-R]的模。

当det[I-R]中ω的实部取自振频率ωˉn，虚部δn取衰减系数时，式（23）为

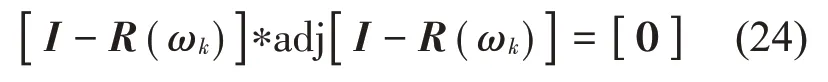
设N是出射波波幅向量dk的维数，m为1≤m≤N的任意正整数，矩阵adj[I-R]的第m列记为dk，则

当结构振动频率等于其自振频率时，adj[I-R(ωk) ]的每一列均可看作是式（25）的解。即adj[I-R(ωk) ]的每一个非零列都可以做为黏弹性地基中单桩在自由振动时非零出射波的波幅向量，求得dk以后，代入式(22)可求得ak，将ak、dk代入式(5)－式(7)中，可求解结构任意点处的位移，将各节点位移归一化处理后即可得到黏弹性地基中单桩的振型曲线。

2 数值结果与分析

与黏弹性地基相互作用的单桩计算模型如图1（a）所示，桩土相互作用用并联的弹簧和黏壶来模拟，桩底为黏弹性支撑，桩径D=1.25 m，泊松比μ=0.2337 ，弹 性 模 量E=4.321×1010Pa ，密 度ρ=267 6 kg m3，截面剪切系数k′=0.82；土体计算参数参考文献[14]中的数值，如表1所列。

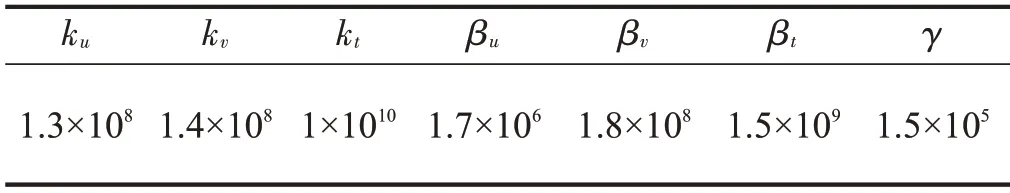
表1 黏弹性地基中土体的计算参数

2.1 埋置长度、外露长度对单桩自振特性的影响

以黏弹性地基中桩底弹性支撑、桩顶自由的单桩为例，根据回传射线矩阵法及求根法，编写计算任意阶数的自振频率和振动模态的MATLAB程序，如表2所列。

表2 3种工况下单桩的埋置长度、外露长度及桩长

图5为埋置长度及外露长度对单桩自振频率的影响。

图5 埋置长度及外露长度对单桩自振频率的影响

由图可知，1 阶自振频率趋于重合，随着黏弹性地基中单桩自振阶数的增大，其自振频率逐渐增大，尤其第4 阶之后，这种增幅很明显；埋置深度相同时，随着外露长度越长，结构的各阶自振频率越小；外露长度相同时，随着埋置深度越深，结构的各阶自振频率越小。

图6 埋置长度及外露长度对单桩衰减系数的影响

图6为埋置长度及外露长度对单桩衰减系数的影响。由图可知，随着黏弹性地基中单桩自振阶数的增大，其衰减系数逐渐增大；埋置深度相同时，随着外露长度越长，结构的各阶衰减系数越小；外露长度相同时，随着埋置深度越深，结构的各阶衰减系数越大。

图7为埋置长度及外露长度对单桩模态的影响。

由图7可知，单桩基础发生自由振动时，埋置长度和外露长度对结构模态并无明显影响；3 种工况下，随着桩长的增大，结构的1 阶振型曲线趋于重合，随着黏弹性地基中单桩自振阶数的增大，其横向位移增大，表明桩长对振型中横向位移的影响较大；埋置部分的横向位移小于外露部分的横向位移，表明黏弹性地基对结构的振动衰减作用明显。

2.2 桩端约束情况对单桩自振特性的影响

图8为桩端约束情况对单桩自振频率的影响。

由图可知，随着黏弹性地基中单桩自振阶数的增大，其自振频率逐渐增大；桩顶固定工况下单桩各阶自振频率最大，桩顶铰接工况下单桩各阶自振频率最小，桩顶自由工况下单桩各阶自振频率略小于

图7 埋置长度及外露长度对单桩模态的影响

图8 桩端约束情况对单桩自振频率的影响

其在桩顶固定工况下的各阶自振频率，又大于其在桩顶铰接工况下的各阶自振频率，这一结果与文献［7］的结论一致。

图9 桩端约束情况对单桩衰减系数的影响

图9为桩端约束情况对单桩衰减系数的影响。由图可知，随着黏弹性地基中单桩自振阶数的增大，其衰减系数逐渐增大；桩顶自由工况下单桩各阶衰减系数最大，桩顶固定工况下单桩各阶衰减系数最小，桩顶铰接工况下单桩各阶衰减系数介于其在桩顶自由和桩顶固定工况下的各阶衰减系数之间。

图10 桩端约束情况对单桩模态的影响

图10为桩端约束情况对黏弹性地基中单桩基础模态的影响。由图可知，桩端相对桩底，其横向位移和轴向位移均增大，表明不同的桩端约束情况对模态的影响较大；桩顶自由工况下单桩各阶振型峰值相对其在桩顶铰接和桩顶固定工况下的各阶振型峰值较小，并且桩顶自由时，随着黏弹性地基中单桩自振阶数的增大，桩端的横向位移逐渐减小。

3 结语

将回传射线矩阵法推广至桩土系统的振动分析中，对比分析了黏弹性地基中桩的外露长度、埋置深度、桩端约束情况对单桩自振频率、衰减系数和模态的影响。得出以下结论：

（1）随着黏弹性地基中单桩自振阶数的增大，其自振频率增幅、衰减系数逐渐增大，尤其是第四阶之后，各阶自振频率增幅很明显。

（2）随着外露长度越长，结构的各阶自振频率和衰减系数越小；随着埋置深度越深，结构的各阶自振频率越小，衰减系数越大。

（3）埋置长度和外露长度对结构的模态并无明显影响，但桩长对振型中横向位移的影响较大；埋置部分的横向位移小于外露部分的横向位移。

（4）桩顶固定工况下单桩各阶自振频率大于其在桩顶铰接和桩顶自由工况下的各阶自振频率；桩顶自由工况下单桩各阶衰减系数大于其在桩顶固定和桩顶铰接工况下的各阶衰减系数；桩顶自由工况下单桩各阶振型峰值相对其在桩顶铰接和桩顶固定工况下的各阶振型峰值较小。