微穿孔板结构吸声仿真技术研究

邢 拓，李贤徽，盖晓玲，蔡泽农，王 芳，关淅文

（北京市劳动保护科学研究所 环境噪声与振动控制北京市重点实验室,北京100054）

微穿孔板结构在实际应用中具有防火、耐腐蚀、能承受高速气流冲击、环境友好等优点。微穿孔板吸声理论首先是由马大猷院士提出[1-2]，其吸声机理可以描述为：薄板上的微孔有近似于空气的声阻抗，微孔通过与空气柱的摩擦，消耗能量，是一种高声阻、低声质量的共振吸声体。通常还会在板后引入空气背腔，提高吸声性能。随着计算能力的提高和复杂流场地引入[3-5]，经典微穿孔板的理论被逐渐完善和扩展。近年微穿孔板复合结构设计被广泛研究[6-7]，但在有限元仿真中由于微孔孔径较小，微穿孔板复合结构的建模难度大。

本文采用有限元软件COMSOL Multiphysics（COMSOL），对微穿孔板结构的吸声性能进行分析计算。为了简化建模难度，使用多孔介质模型和内置穿孔板模型进行简化计算，同时依靠微孔建模和经典理论计算相互验证。

1 微穿孔板理论

1.1 经典微穿孔板理论

在经典微穿孔板理论[1-2]中通过吸声带宽的计算，当1＜k＜10 时，不需要用其他吸声材料就能够达到较宽的吸声带宽，k为微穿孔板常数

微穿孔板的相对声阻抗率为

其中：穿孔板的相对声阻率和相对声抗率为

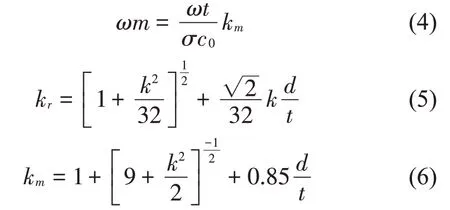
其中：d、t、σ、η分别为孔径、板厚度、穿孔率和空气运动黏度。

当包含空气背腔D时，背腔相对声阻抗率为

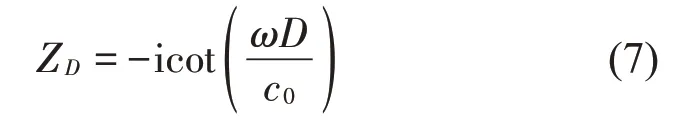
因此，整体结构的相对声阻抗率为

当声波垂直入射时，微穿孔板吸声结构的吸声系数为

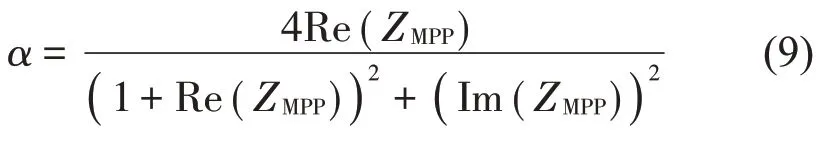
1.2 多孔介质模型

选择多孔介质模型中Johnson-Champoux-Allard(JCA)模型[8-9]，该模型可以用来等效微穿孔板和帘幕结构，其相对声阻抗率为

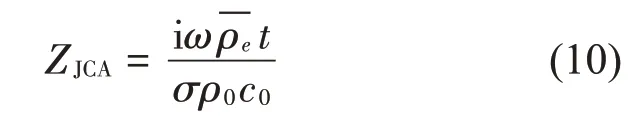
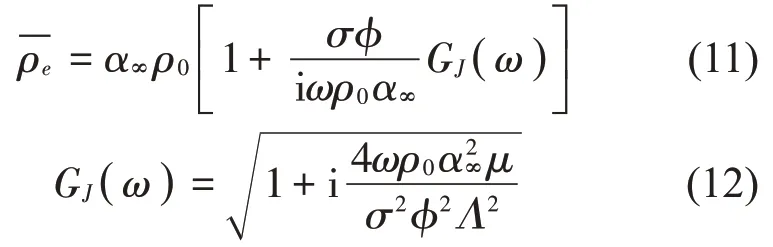
其中：曲折系数α∞

在文献[8]中εe取值为

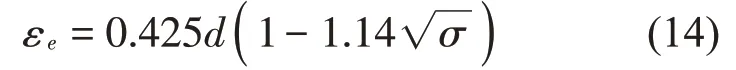
孔是圆孔时流阻为

其中：黏性特征长度等于热特征长度为

2 建模方法

2.1 微孔建模

通常微穿孔板结构的孔径远小于背腔尺寸，为了节约计算空间，先计算微穿孔板的阻抗，再计算整体结构的吸声。由于微孔较小，需考虑孔内黏滞损耗和热损耗，因此选择三维黏热声学频域模块。非线性损耗通常发生在高声量级（或流体经过微穿孔板）的情况，在此仅考虑其线性效应，同时忽略孔间影响。由于圆孔的对称性，选择1/4 结构建模，设置对称边界。设置背景声压场和完美匹配层，其中背景声压场选择垂直向上幅值为1 Pa 的平面波辐射，其具体模型如图1所示。

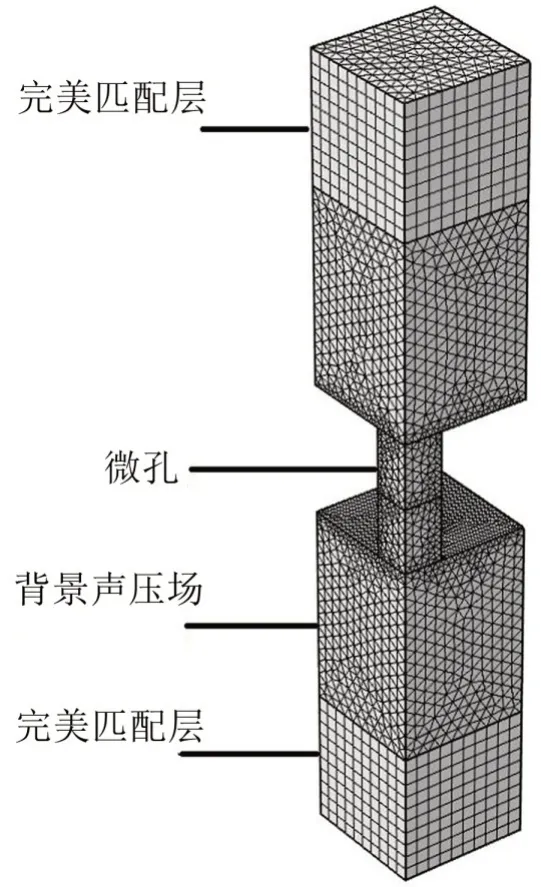
图1 微穿孔板微孔模型

微穿孔板结构参数如表1所示。参数组一属于随机选取，参数组二是参考了文献[1-2]中关于孔径与板厚的讨论而选取，参数组三是因为微孔加工能力的提高而选取。声速为340 m/s，空气密度为1.2 kg/m3，空气动力黏度μ为1.8×10-5Pa·s。以参数组一为例，该模型自由度为749 399。

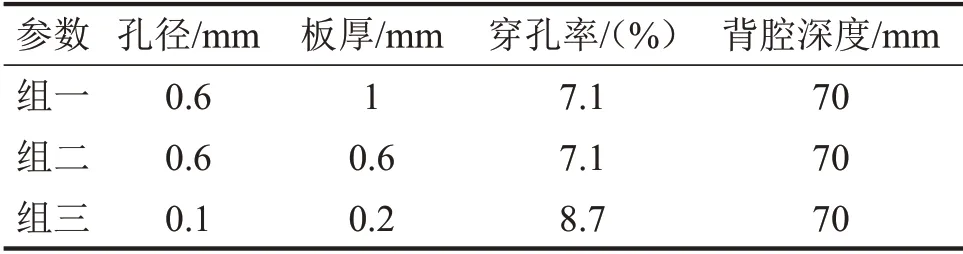
表1 选取微穿孔板结构参数

2.2 多孔介质建模

选择JCA 模型计算微穿孔板结构的吸声系数。以参数组一为例，可以计算出相应的流阻率为22 646.8 Pa·s/m2，黏性特征长度和热特征长度都为0.3 mm，曲折系数为1.36。为了节约计算空间，选择二维轴对称压力声学频域模块，选择幅值为1 Pa 的平面波入射，入射方向为垂直向下。需要特别注意的是，吸声系数可以写为

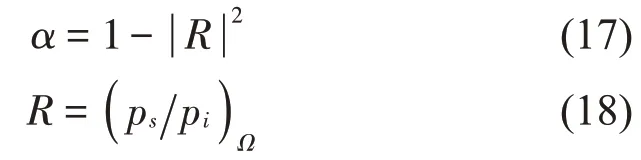
其中：ps为散射声压，pi为入射声压，Ω代表空气域和材料域相交边界上的平均算子。在COMSOL 中输入时，除了选取空气域和多孔材料域的边界做线平均，还需输入down作为计算边界的下部算子。该模型求解自由度11 448，计算频率的步长为5 Hz。

2.3 内置穿孔板建模

利用内置穿孔板模型也可以实现微穿孔板结构的仿真。该软件的内置穿孔板模型主要是基于Crandall 对于Rayleigh 微管中声波分析结果的简化推导。该模型可以设置孔间影响，其默认不计孔间相互作用。该模型还内置了声阻抗的末端修正，其中声抗的末端修正与经典理论相同。内置穿孔板模型属于内部辐射边界，因此需要设定空气背腔。穿孔板中流体材料选择空气。内部穿孔板存在方向性，由其在建模时所处y轴的位置决定，当处于的y轴为非负时，方向朝向y轴正方向，当处于的y轴为负时，方向朝向y轴负方向。在此选择y=0，即其朝向为y轴正方向。设置幅值为1 Pa 的平面声波，同样朝向y轴正方向，位于内部穿孔板下方。其吸声系数计算仍使用式(17)和式(18)，依然选取计算域的下部，但其实际意义与多孔介质模型中不同。该模型求解自由度7 956，计算频率步长为5 Hz。

3 结果

有限元和经典理论计算的微穿孔板（不含背腔）的相对声阻率和相对声抗率的结果如下三组图所示。以参数组一为例，其中微孔建模方法计算时长约34.5 h，多孔介质建模方法计算时长约112 s，内置穿孔板建模方法计算时长约78 s。如图2－图3所示。

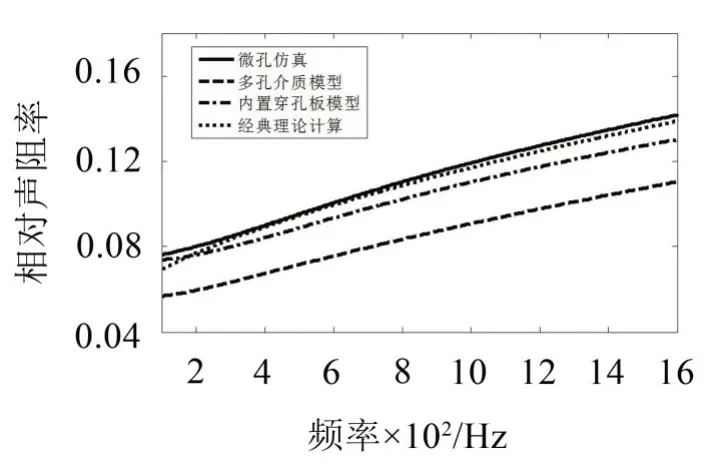
图2 参数组一仿真和经典理论计算的声阻

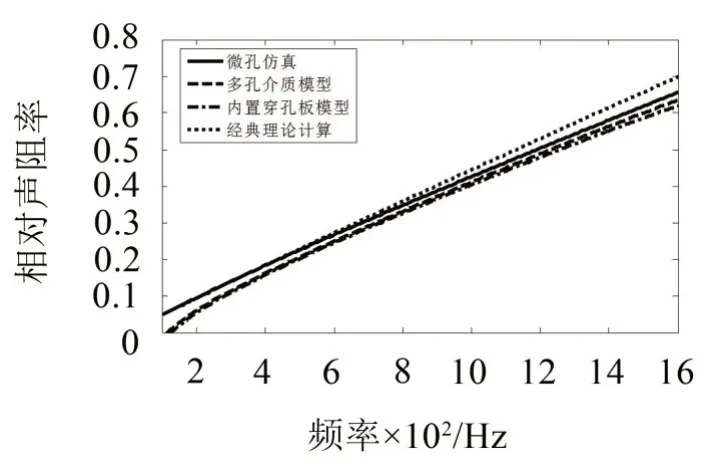
图3 参数组一仿真和经典理论计算的声抗

由图2可知，多孔介质模型计算声阻相对较小，微孔仿真和经典理论计算结果基本吻合。由图3可知，四种计算的声抗结果基本一致，经典理论计算的结果在高频处大于其他计算结果。

参数组二与参数组三的声阻和声抗结果如图4到图7所示。

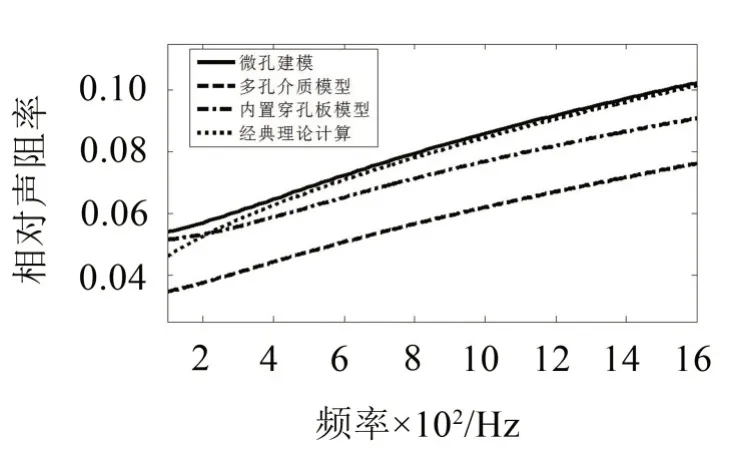
图4 参数组二仿真和经典理论计算的声阻

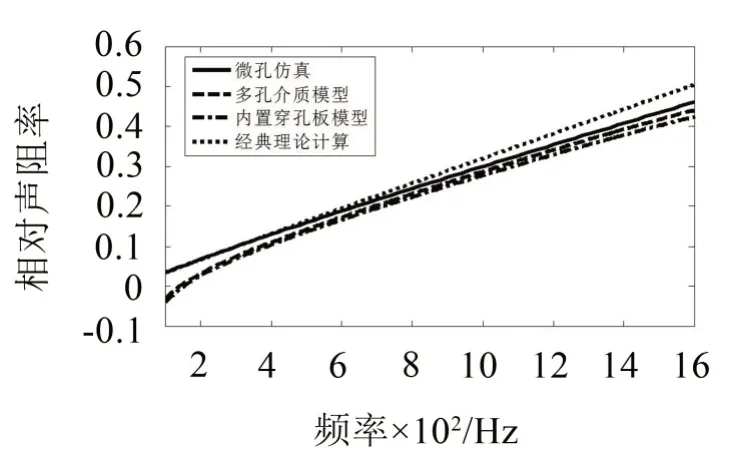
图5 参数组二仿真和经典理论计算的声抗

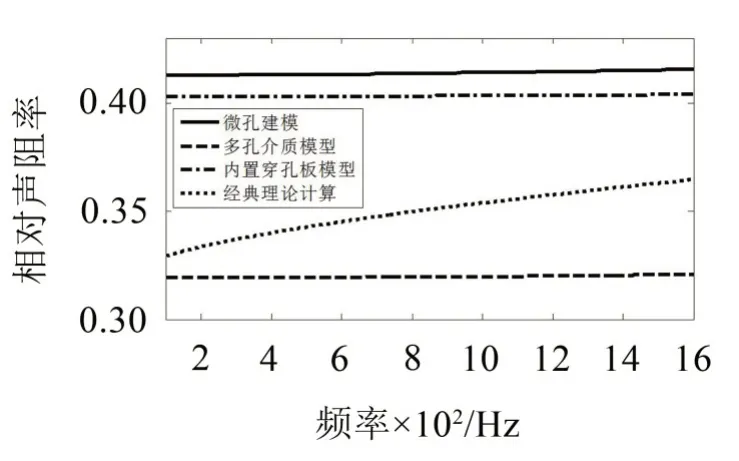
图6 参数组三仿真和经典理论计算的声阻

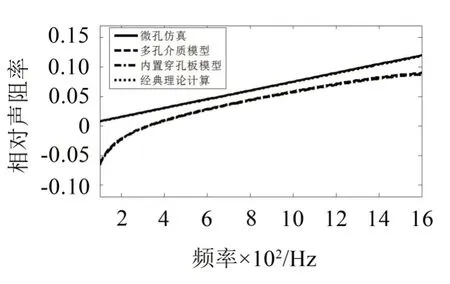
图7 参数组三仿真和经典理论计算的声抗

其中多孔介质模型计算的声阻较小，当孔径为0.1 mm时，经典理论计算的声阻也较小。在参数组二中声抗曲线基本重合，在参数组三中多孔介质模型和内置穿孔板模型计算的声抗相对较低。

4 讨论

在参数组一的微孔建模中，选择过孔心并垂直于xy平面的截面，在1 000 Hz 时其微孔声压分布和瞬时局部速度如图8和图9所示。

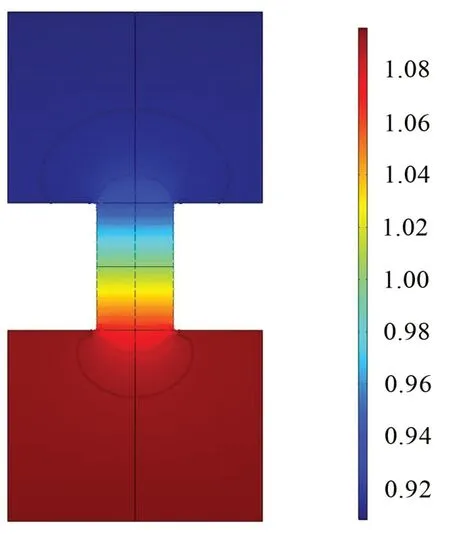
图8 1 000 Hz微孔声压分布

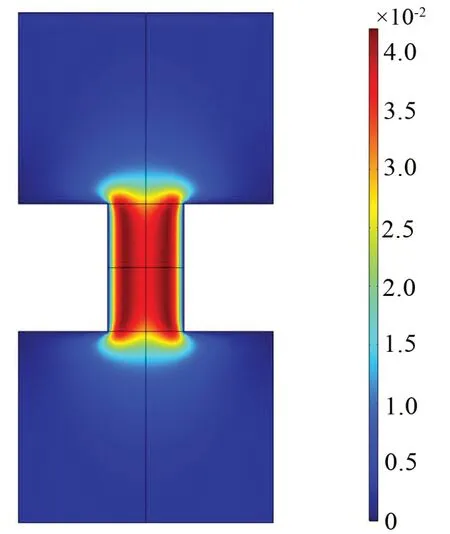
图9 1 000 Hz微孔瞬时局部速度

由图8可知，声压幅值通过微孔明显减小。由图9可知，内壁面速度基本为零，从壁面到中心，运动速度呈现先增加、后减小的趋势，最大速度出现在壁面黏滞层厚度之外，并未出现在孔心处，孔口处声速呈现扇形分布。结合图2和图3可知，微孔建模和经典理论计算并不完全重合，其差别主要在于理论的末端修正部分，已有学者[3-5]对于经典理论中的末端修正进行了详细分析，其结果表明：经典理论中末端声辐射导致的声抗修正略大于黏热计算结果，沿板的流阻导致地声阻修正与频率相关，该结果与图2和图3结果一致。

结合表1中3组微穿孔板结构参数，利用3种仿真方法分别计算微穿孔板结构的吸声系数，其结果如图10到图12所示。

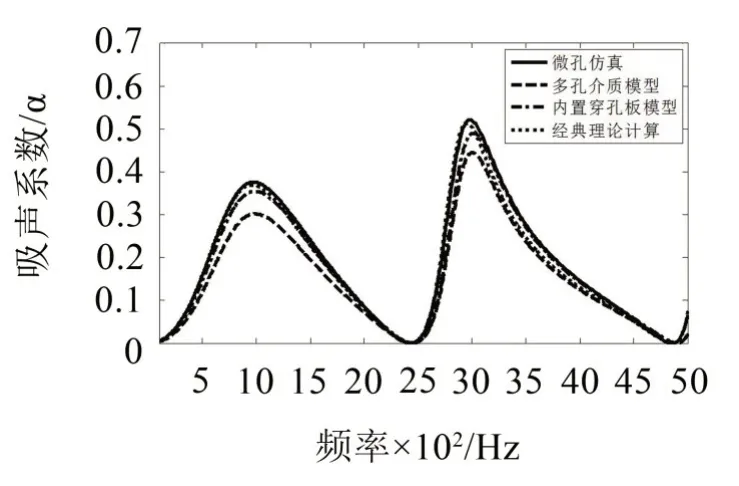
图10 参数组一仿真和理论计算的吸声系数

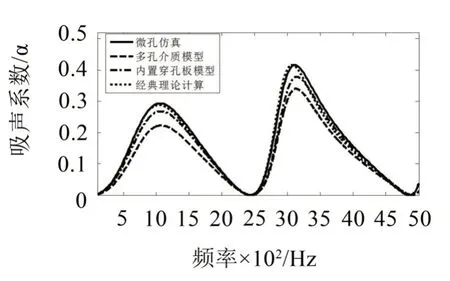
图11 参数组二仿真和理论计算的吸声系数

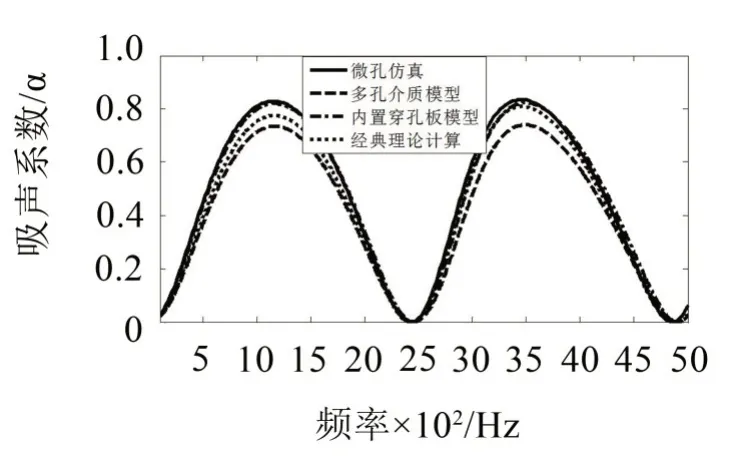
图12 参数组三仿真和理论计算的吸声系数

由该三图可知，仿真曲线和理论计算曲线的趋势完全吻合，多孔介质模型计算的吸声曲线的峰值略低于其他3 种结果，该结果与文献[9]中描述结果相同，即在第一峰值处对于黏性耗散估计不足，而实际情况为对所有峰值估计不足。由图10和图11可知，微孔仿真、内置穿孔板模型和经典理论计算的结果基本吻合。在图12中，经典理论计算峰值也较低，这是因为经典理论要求微穿孔板常数在1～10之间，对于孔径0.1 mm 的微孔而言，在1 000 Hz 时微穿孔板常数才等于1，因此利用此公式计算会导致声阻估计不足。

5 结语

针对微穿孔板结构采用微孔建模、多孔介质模型和内置穿孔板模型建模的3种有限元方法进行了研究。其中微孔结构仿真利用黏热声学耦合模块，有助于完善经典微穿孔板理论。其中多孔介质模型计算结果的声阻估计不足，在吸声峰值处低于其他结果。内置穿孔板模型计算的吸声曲线与微孔仿真和经典理论计算结果吻合较好，可以利用内置穿孔板模型简化仿真难度，提高了计算速度，同时也可以保证可靠的吸声计算结果。