灵活选解法 方程巧计算

文焦倩玉

亲爱的同学们，你们知道吗，人类认识一元二次方程的历史相当久远。阿拉伯数学家阿尔·花拉子米在他的著作《代数学》里第一次承认了一元二次方程有两个根，还用几何学方法得出一般的求根公式，极大地推动了数学的发展。我们都知道解一元二次方程常见的方法有直接开平方法、配方法、公式法和因式分解法，下面我们一起来结合具体题目，合理选择解一元二次方程的方法，以方便我们的计算。

一、直接开平方法

例1 解方程：（x+1）2-1=3。

【解析】把x+1看作一个整体，将方程两边同时加1，变形为（x+1）2=4，再直接开平方，计算即可。

解：（x+1）2-1=3。

（x+1）2=4。

x+1=±2。

x=-1±2。

∴x1=1，x2=-3。

【点评】形如（x+h）2=k（h、k为常数，k≥0）的方程通常使用直接开平方法。需要注意的是，若k=0，则答案需写作x1=x2=-h的形式，方程有两个相等的实数根。

二、配方法

例2 解方程：x2-10x+22=0。

【解析】观察这个一元二次方程，我们发现二次项系数为1，一次项系数为偶数，此时考虑选择使用配方法。

解：x2-10x=-22。

x2-10x+52=-22+52。

【点评】关于x的一元二次方程ax2+bx+c=0（a、b、c是常数，a≠0），当a=1，b为偶数时通常使用配方法。先把常数项移到方程的右边，然后加上一次项系数的一半的平方。将方程转化为（x+h）2=k的形式，进而求解。当一元二次方程的一次项系数不是偶数时，配方容易出错，同学们应引起注意。

三、公式法

例3 解方程：2x2+x-1=0。

【解析】观察这个一元二次方程，我们发现二次项系数不为1，一次项系数为奇数，此时应选择使用公式法。

解：∵a=2，b=1，c=-1，

b2-4ac=12-4×2×（-1）=9。

【点评】关于x的一元二次方程ax2+bx+c=0（a、b、c是常数，a≠0），当b2-4ac≥0时，方程的实数根是x=同学们对一元二次方程的求根公式需要熟练掌握，把各项系数的值直接代入公式，进而求解。特别对于a≠1，b为奇数的情况，公式法通常较为简便。

四、因式分解法

例4 解方程：x（2x-1）=3（1-2x）。

【解析】观察这个一元二次方程，我们发现2x-1与1-2x互为相反数，移项后可提公因式，因此应选择使用因式分解法。

解：x（2x-1）-3（1-2x）=0。

x（2x-1）+3（2x-1）=0。

（2x-1）（x+3）=0。

∴2x-1=0或x+3=0。

【点评】开始动笔做题之前，同学们一定要养成认真读题的好习惯。这道题可通过移项，将方程右边化为0，方程左边经提公因式之后可分解为两个一次因式的乘积。把解这样的一元二次方程转化为解两个一元一次方程，从而得出结果。

小弱沮丧地趴在桌上，远远看上去就像是喝醉了，不过坐在他身边的安洁西却看到他呆滞地盯着地面的眼睛里满是清醒。

例5 解方程：（3x-1）2-4x2=0。

【解析】将4x2看作2x整体的平方，我们可以利用平方差公式将这个一元二次方程的左边进行因式分解，转化成两个一次因式的乘积。

解：（3x-1）2-（2x）2=0。

（3x-1+2x）（3x-1-2x）=0。

（5x-1）（x-1）=0。

∴5x-1=0或x-1=0。

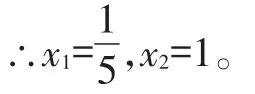
【点评】形如x2-ax=0和x2-a2=0的一元二次方程通常可以使用因式分解法快速地解决。

例6 已知关于x的方程2x2+mx+50=0的一个根是10，求它的另一个根。

【解析】已知一元二次方程的一个根，可以将此根代入方程求出参数的值，再通过解这个方程得到它的另一个根。或者根据题目条件，利用根与系数的关系，进行求解。

解法一：把x=10代入，得2×102+10m+50=0。

解得m=-25。

把m=-25代入，得2x2-25x+50=0。

∵a=2，b=-25，c=50，

【点评】对比本题的这两种解法，我们可以明显看出方法2更为便捷。已知一元二次方程ax2+bx+c=0（a、b、c是常数，a≠0）中a和b的值，可以利用x1+x2=进行求解；已知a和c的值，则可以利

例7 已知关于x的方程x2+bx+c=0的两根分别是 2+1、 2-1，求b、c的值。

【解析】已知一元二次方程的两个根，那么我们可以直接代入，联立得到关于b和c的二元一次方程组，进而求解。经过计算，我们发现这种方法并不方便。我们可以逆向使用根与系数的关系，直接得到b和c的值。

解：∵x1+x2=-b，

【点评】此处为根与系数的关系的直接应用，同学们要注意归纳总结。另外中，负号不要漏写。