模块复习固解法 内在联系串题型

文诸士金

一元二次方程的复习一般可以分为基本概念、解法及相关知识（根与系数关系、根的判别式）、应用等主要模块。我们通过这样的模块复习会感觉比较清晰，寻找知识的内在联系应遵循知识的生长结构。下面和同学们以模块复习的方式共同梳理一元二次方程的知识。

一、以小题组合梳理概念，利于知识记忆

同学们都知道，数学学习不能死记硬背，在一元二次方程的学习中并不是强行记住方程的概念、根的概念就等于掌握了知识。死记硬背数学概念不仅不利于对知识的理解，还会让同学们感觉数学学习过于单调，容易失去对数学学习的兴趣。因此我们在复习一元二次方程的概念时，建议大家以题为载体进行复习，避免知识的机械记忆。

例1 （1）一元二次方程（x+1）（x+3）=9的一般形式是_______，二次项系数为_______，常数项为_______。

（2）关于x的方程x2+mx+6=0的一个根为-2，则另一个根是________。

（3）请写出一个关于x的一元二次方程________，使它的两根分别为-2和3。

以上三组小题各有特色，第（1）小题是以具体的题来巩固我们对一元二次方程一般形式的认识。对于这个认识的具体要求，我们切莫以为是简单地记住ax2+bx+c=0（a≠0）即可，具体分解对这个概念的认识，就是要首先会将其他形式的方程变成这个“样子”，这个同解变形也是所有方程解法的根本所在。我们借助同解变形，可以将一个不熟悉的“样子”变成熟悉的“样子”。需要说明的是，这样的同解变形一般主要依据“等式性质”。故这个方程的一般形式是x2+4x-6=0，二次项系数为1，常数项为-6。

第（2）小题和第（3）小题是立足于一元二次方程根的概念进行的考查，这样的小题既可以从根的概念的本质（即能使得方程成立的未知数的值）上去理解完成，也可以从后续解法学习中获得的根与系数关系（韦达定理）来完成。第（2）小题的另一个根是-3，而第（3）小题两个根为-2和3，那么其对应的方程可以为（x+2）（x-3）=0。

像这样融基础知识于小题，便于我们以题为舟，横渡概念之河。

二、以内在联系巩固解法技能，强于题海盲渡

在一元二次方程复习中，具体的解法是复习的重点。我们往往是以大量的题目来巩固新课学习的解题方法，做错了就订正，然后继续做。茫茫题海，没有方向。很多时候，同学们还是停留在教材梳理出的“直接开方法”“配方法”“求根公式法”“因式分解法”等表层认知上，认为这些方法都是独立并存的，没有深层次理解解法背后的联系。这里我们简单地梳理一下：

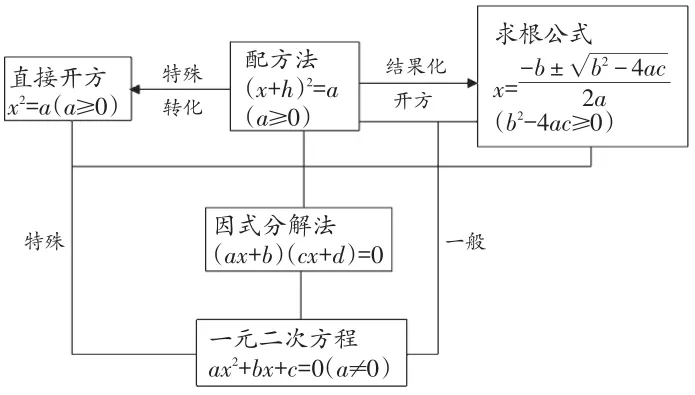
根据这个梳理，其实比较容易理解四种解法之间的关系，选择优化解法时，就会有明确的方向。再辅以如例2的典型例题加以巩固。

例2 解下列方程：

（1）x2+2x-8=0；

（2）x-2=2x-x2；

（3）（2x+1）（x-3）=3。

这三个小题，在方法选择上要有侧重，一般有两个层次要求，一是要能够正确解出，不管用什么方法；二是要能够选择较好的方法快速解出。这样既是考查同学们计算技能的掌握情况，也有利于同学们培养思维的敏捷性。下面的解法和答案供参考：

（1）x2+2x-8=0。

解：（x+4）（x-2）=0。

∴x1=-4，x2=2。

（2）x-2=2x-x2

解：x-2=-x（x-2）。

x-2+x（x-2）=0。

（x-2）（1+x）=0。

∴x1=2，x2=-1。

（3）（2x+1）（x-3）=3。

解：2x2-5x-6=0。

a=2，b=-5，c=-6，

b2-4ac=73，

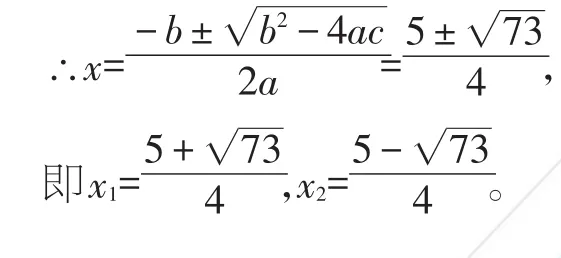
三、以综合拓展多样呈现，便于见多识广

在解法和概念的复习过程中有两个知识难点，一个是根的判别式，另一个是根与系数的关系（韦达定理）。我们从现有的知识学习体系中理解，这两部分知识可以独立地进行应用，但不可忽视这两部分知识与一元二次方程本身解法的内在联系。根的判别式缘起配方法的过程，当然这里对根的判别目前是在实数范围内，到了高中阶段会出现虚根的情况。而韦达定理可以从求根公式来推得，这样同学们就可以自己进行推演。这两个知识点的考查，可以以小综合形式多样呈现，避免单独考查带来与实际考试题型的脱节。

例3 已知关于x的一元二次方程x2-（k+1）x+2k-2=0。

（1）求证：方程有两个实数根；

（2）若△ABC的两边AB，AC的长是这个方程的两个实数根，第三边BC的长为3，当△ABC是等腰三角形时，求k的值。

（1）证明：

∵Δ=［-（k+1）］2-4（2k-2）=k2-6k+9=（k-3）2≥0，

∴方程有两个实数根。

（2）解：x2-（k+1）x+2k-2=0，

（x-2）（x-k+1）=0，

解得x1=2，x2=k-1，

当k-1=3时，△ABC是等腰三角形，则k=4；

当k-1=2时，△ABC是等腰三角形，则k=3，

所以k的值为4或3。

例3考查了一元二次方程ax2+bx+c=0（a≠0）的根的判别式Δ=b2-4ac：当Δ＞0，方程有两个不相等的实数根；当Δ=0，方程有两个相等的实数根；当Δ＜0，方程没有实数根。其第（2）小问融入了三角形三边关系、等腰三角形知识，逐步加强对k的条件限制，以确定k的取值。

例4 已知关于x的方程x2-2x+m=0有两个不相等的实数根x1、x2。

（1）求实数m的取值范围；

（2）若x1-x2=2，求实数m的值。

例4的呈现从有两个不相等的实数根开始，确定b2-4ac＞0，得到m的范围，再结合x1-x2=2，根据根与系数关系，求m的值。

解：（1）由题意得：Δ=（-2）2-4×1×m=4-4m＞0，

解得：m＜1，

即实数m的取值范围是m＜1。

（2）由根与系数的关系得：x1+x2=2，

又x1-x2=2，

解得：x1=2，x2=0，

由根与系数的关系得：m=2×0=0。

这里我们主要是从模块复习的角度梳理了一元二次方程的基础知识和基本技能的考查类型，还不够全面，仅供同学们复习参考。我们在后续的学习过程中要认识到，很多时候技能方法不是孤立的，高次方程的降次思想、多元方程的消元思想是一以贯之的，是所有模块知识的内在“血脉”。