方程模型有途径 表格策略寻等量

文李 丹

方程是刻画现实世界数量关系的有效模型。同学们已经学习了一元一次方程、二元一次方程组、分式方程和一元二次方程等知识，感受了方程模型对解决实际问题的作用和价值，积累了一些利用方程解决问题的经验，即寻找等量关系，必要时可以通过表格帮助我们理清已知与未知的关系，从而列出方程求解。一元二次方程解决问题的基本类型有：图形面积问题、变化率（增长或下降）问题、销售利润问题等。

一、图形面积问题

例1 南京市某小区有一块长12米、宽6米的矩形空地，计划在其中修建两块相同的长方形绿化地，它们的面积之和为36平方米，两块绿化地之间及周围留有宽度相等的小路，求小路的宽度为多少米？

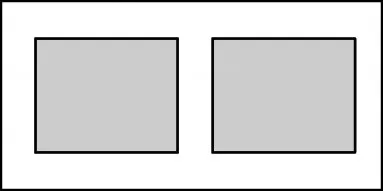
【解析】本题可以把两个绿化矩形拼成一个大矩形，此大矩形的面积为36，找到该矩形的长与宽，其乘积为36建立一元二次方程求解。

解：设小路的宽度为x米，根据矩形的面积公式可得一元二次方程：（12-3x）（6-2x）=36。解这个方程，得 x1=1，x2=6（不合题意，舍去）。

答：小路的宽度为1米。

【点评】本题是典型的图形面积问题，除了拼接大矩形解决问题外，还可以用整个图形的面积减小路面积，得到两块矩形绿化地面积36，建立方程求解。解决此类问题时，同学们最关键的就是找到图形之间的面积关系。

二、变化率（增长或下降）问题

例2 为了巩固全国文明城市建设成果，突出城市品质的提升，近年来，某市积极落实节能减排政策，推行绿色建筑。据统计，该市2014年的绿色建筑面积约为700万平方米，2016年达到了1183万平方米，若2015年、2016年的绿色建筑面积按相同的增长率逐年递增，求这两年该市推行绿色建筑面积的年平均增长率。

【解析】设这两年该市推行绿色建筑面积的年平均增长率为x，本题可借助表格分析数量关系：

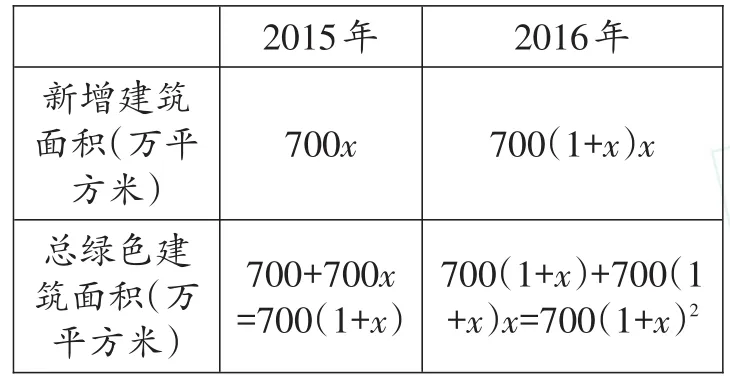
__________________________________2015年2016年____新增建筑面积（万平__方________________________________米）总绿色建筑面积（万__平方米）700x 700（1+x）x 700+700x=700（1+x）700（1+x）+700（1+x）x=700（1+x）2

2016年总绿色建筑面积为1183。再根据相等关系建立一元二次方程求解。

解：设这两年该市推行绿色建筑面积的年平均增长率为x，由题意得：

700（1+x）2=1183，

解得：x1=0.3，x2=-2.3（不合题意，舍去）。

答：这两年该市推行绿色建筑面积的年平均增长率为30%。

【点评】本题是基本的增长率问题，同学们真正理解a（1+x）n的意义是解决问题的关键。

例3 某种商品经过两次连续降价后，单价由200元下调至128元，求这种商品平均每次降价的百分率。

【解析】设这种商品平均每次降价的百分率为x，本题可借助表格分析数量关系：

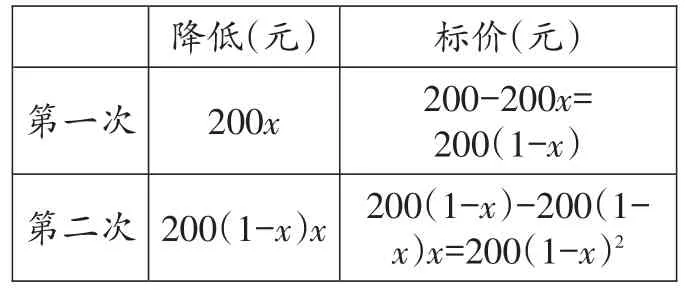
_________________________标价（元）200-200x=200（1-x）____200（1-x）-200（1-____________________x）x=200（1-x）2第一次降低（元）__________________200x第二次200（1-x）x

两次降价后标价128元。再根据相等关系建立方程求解。

解：设这种商品平均每次降价的百分率为x，根据题意得：200（1-x）2=128，

解得：x1=0.2，x2=1.8（不合题意，舍去）。

答：这种商品平均每次降价的百分率为20%。

【点评】本题是基本的下降率问题，同学们真正理解a（1-x）n的意义是解决问题的关键。

三、销售利润问题

例4 我区正大力发展绿色农产品，有一种有机水果A特别受欢迎，某超市以市场价格10元每千克在我市收购了6000千克A水果，立即将其冷藏，请根据下列信息解决问题。

①水果A的市场价格每天每千克上涨0.1元；

②平均每天有10千克的该水果损坏，不能出售；

③每天的冷藏费用为300元；

④该水果最多保存110天。

（1）若将这批A水果存放x天后一次性出售，则x天后这批水果的销售单价为______元；可以出售的完好水果还有______千克；

（2）将这批A水果存放多少天后一次性出售所得利润为9600元？

【解析】（1）根据销售价=成本价+每天每千克上涨0.1元填空；完好水果的质量=总质量-损坏的水果的质量；

（2）按照等量关系“利润=销售总金额-收购成本-各种费用”列出方程求解即可。

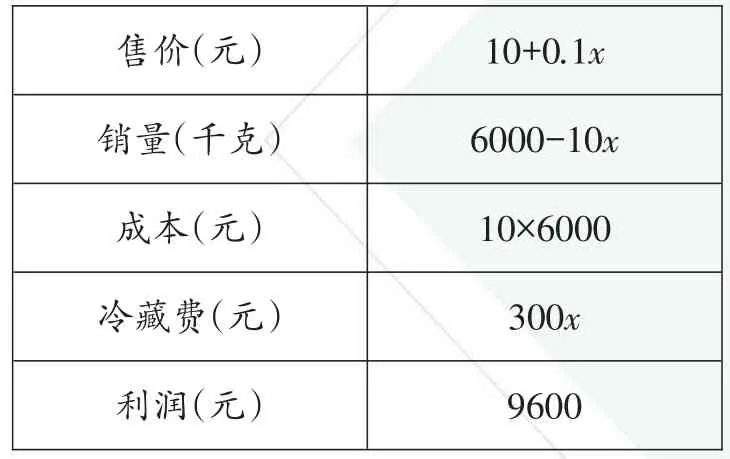
售价（元）____销量（千克）成本（元）冷藏费（元）利润（元）10+0.1x 6000-10x_____10×6000 300x 9600

可借助表格分析各个量的表示：；

【解答】（1）10+0.1x；6000-10x；

（2）由题意列方程：

（10+0.1x）（6000-10x）-10×6000-300x=9600，

解得：x1=80，x2=120（不合题意，舍去）。

答：这批A水果存放80天后一次性售出所得利润为9600元。

【点评】本题是典型的销售利润模型，等量关系一般为：（售价-成本）×销售量=总利润，其中售价和销售量都跟价格有关，从而据此设定未知量建立方程。

小试牛刀

1.有一条长40cm的绳子，要把它围成一个矩形，若设矩形的一边长为xcm，回答以下问题：

（1）怎样围成一个面积为75cm2的矩形？

（2）能围成一个面积为101cm2的矩形吗？如能，说明围法；如不能，说明理由。

2.为了建设生态园林城市，某市大力开展植树造林活动，该市林业部门调查情况如下表：

2011年底21.6年份全市森林拥有面积（万亩）2009年底15

求2009年底至2011年底该市森林拥有面积的年平均增长率。

3.某玩具厂生产一种玩具，按照控制固定成本降价促销的原则，为使生产的玩具能够及时售出，据市场调查：每个玩具按480元销售时，每天可销售160个；若销售单价每降低1元，每天可多售出2个。已知每个玩具的固定成本为360元，问这种玩具的销售单价为多少元时，厂家每天可获利润20000元？

4.某水果店销售一种水果的成本价是5元/千克。在销售过程中发现，当这种水果的价格定在7元/千克时，每天可以卖出160千克。在此基础上，这种水果的单价每提高1元/千克，该水果店每天就会少卖出20千克。

（1）若该水果店每天销售这种水果所获得的利润是420元，则单价应定为多少？

（2）在利润不变的情况下，为了让利于顾客，单价应定为多少？