“火眼金睛”辨模型 解决“线、角”问题灵

文陈 俊

全等三角形判定的关键在于认知并熟练掌握全等三角形的几种判定方法，而难点在于在较复杂的图形中，灵活运用判定方法找出全等三角形，从而解决“线、角”问题。要迅速找出全等三角形，需要我们熟知全等三角形的常见模型。下面，简要说明与等腰三角形有关的两种模型。

一、“手拉手”模型

1.模型说明

如图1，△ABC、△ADE均为等腰三角形，AB=AC，AD=AE，∠BAC=∠DAE，连接BD、CE，根据“SAS”，易证△ABD≌△ACE。若将△ADE绕点A旋转一定的角度，如图2、图3，则△ABD≌△ACE仍然成立。

图1

图2

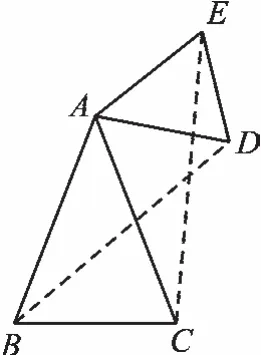
图3

该模型是由有公共顶点且顶角相等的等腰三角形构成。“手拉手”模型常应用于旋转题型，在旋转变化的同时，始终存在一对全等三角形。

如果把小等腰三角形的腰长看作小手，把大等腰三角形的腰长看作大手，类似大手拉着小手，所以这个模型也被称为“手拉手”模型。

2.模型应用

如图4，△ABC、△ADE均为等腰三角形，AB=AC，AD=AE，∠BAC=∠DAE，连接BE、CD交于点F，BE、AC交于点G。求证：（1）BE=CD；（2）∠BFC=∠BAC；（3）连接AF，AF平分∠BFD。

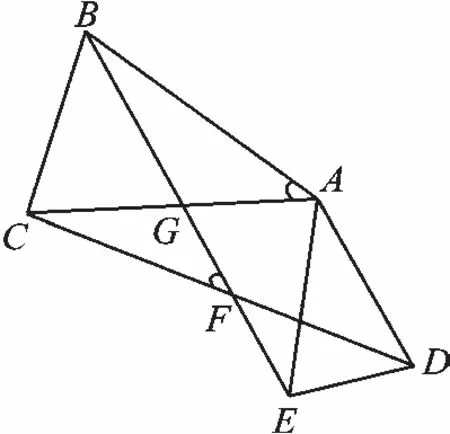
图4

图5

证明：（1）∵∠BAC=∠EAD，

∴∠BAE=∠CAD。

在△ABE和△ACD中，

∴△ABE≌△ACD（SAS），∴BE=CD。

（2）∵△ABE≌△ACD，∴∠ABE=∠ACD。

∵在△ABG和△FGC中，∠ABE=∠ACD，∠AGB=∠FGC，∴∠BFC=∠BAC。

（3）如图5，过点A分别作AH⊥BE、AI⊥CD，垂足分别为点H、I。

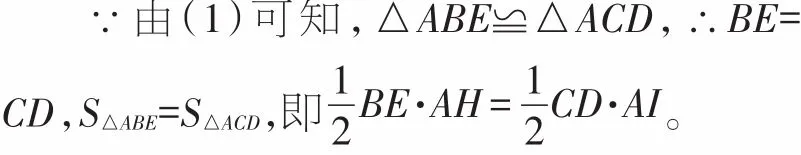
∴AH=AI，∴Rt△AHF≌△Rt△AIF。

∴AF平分∠BFD。

小结：本题证明的结论均与“线、角”有关，我们只需挖掘出“手拉手”模型，发现全等三角形，再利用全等三角形的性质解题就水到渠成了。

3.模型拓展——从一般到特殊

图6

图7

图8

图9

如图6，若△ABC和△DCE均为等边三角形，则△CAE≌△CBD；

如图7，若△ABC和△ADE均为等腰直角三角形，则△ACD≌△ABE；

如图8，若四边形ABCD和四边形AEFG均为正方形，则△ADG≌△ABE。

二、“半角”模型

1.模型说明

如图9，△ABC中，AB=AC若在△ABC外部作△ABF，且∠4=∠3，AF=AE，则△ABF≌△ACE。

我们习惯把过等腰三角形顶角的顶点引两条射线，使两条射线的夹角为等腰三角形顶角的一半的模型称为“半角”模型。

2.模型应用

如图10，已知△ABC是等边三角形，点D是△ABC外一点，DB=DC且∠BDC=120°，∠EDF=60°，DE、DF分别交AB、AC于点E、F。

求证：EF=BE+CF。

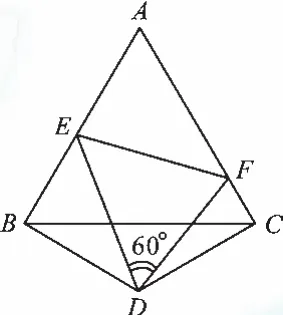
图10

图11

思路：如图11，将△BDE绕点D旋转至△CDG，使△BDE≌△CDG。

∵DB=DC且∠BDC=120°，∴易证∠EBD=∠GCD=90°，F、C、G三点共线。

在△EDF和△GDF中，

∵ED=GD，∠EDF=∠GDF=60°，DF=DF，

∴△EDF≌△GDF，∴EF=GF。

∵GF=GC+CF=BE+CF，∴EF=BE+CF。

3.模型拓展——从一般到特殊

如图12，在正方形ABCD中，E、F分别是BC、CD边上的点，∠EAF=45°，求证：（1）EF=BE+DF；（2）C△CEF=2AB。

图12

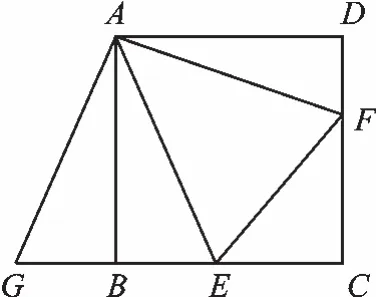
图13

思路：（1）将△ADF绕点A顺时针旋转90°，可得△ABG（如图13），则△ADF≌△ABG，易证△AGE≌△AFE，∴GE=EF。

∵GE=GB+BE=DF+BE，∴EF=BE+DF。

（2）由（1）得，EF=BE+DF，

小结：利用“半角”模型，先将“半角”两边的三角形旋转到一边，合并形成新的三角形，接着证明与“半角”所在的三角形全等，最后通过全等的性质得出线段之间的数量关系，从而解决问题。