错要追因 纠要有据

文古作军

文古作军

一、利用三个角对应相等证明全等出错

例1如图1，∠CAB=∠DBA，∠C=∠D，E为AC和BD的交点。△ADB与△BCA全等吗？并说明理由。

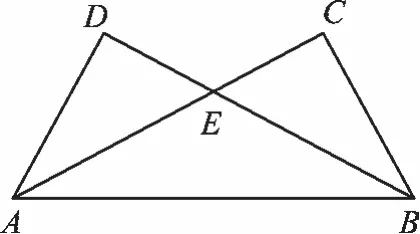
图1

【错解】△ADB≌△BCA。

∵∠C=∠D ，∠CAB=∠DBA，∴∠DAB=∠CBA，∴△ADB≌△BCA（AAA）。

【知错】两个三角形全等结论是对的，但三个角对应相等不能作为三角形全等的判定条件。证明三角形全等，至少要有一条边对应相等。因为角决定三角形的形状，边决定三角形的大小。

【正解】△ADB≌△BCA。

∵∠CAB=∠DBA，∠C=∠D，AB=BA（公共边），∴△ADB≌△BCA（AAS)。

二、利用两边及一边的对角对应相等证明全等出错

例2如图2，已知△ABC中，AB=AC，D、E分别是AB、AC的中点，且CD=BE。△ADC、△AEB全等吗？并说明理由。

图2

【错解】△ADC≌△AEB。

∵AB=AC，BE=CD，∠A=∠A，

∴△ADC≌△AEB（SSA）。

【知错】错解在于把“SSA”作为三角形全等的判定条件，这是全等三角形证明题中最典型的错误。实际上，“SSA”不能作为三角形全等的判定条件。两边及一边的对角相等的两个三角形全等需要附加条件才能成立。

【正解】△ADC≌△AEB。

∵AB=AC，D、E为AB、AC的中点，

∴AD=AE。

在△ADC和△AEB中，

∵AB=AC，AD=AE，CD=BE，

∴△ADC≌△AEB（SSS）。

三、利用等式的性质证明三角形全等出错

例3如图3，已知AC、BD相交于点O，∠A=∠B，∠ACD=∠BDC，AD=BC。试说明△AOD≌△BOC。

图3

【错解】在△ADC和△BCD中，

∵∠A=∠B，∠ACD=∠BDC，DC=CD，

∴△ADC≌△BCD（AAS），

∴△ADC-△DOC=△BCD-△DOC，

即△AOD≌△BOC。

【知错】错解将等式的性质盲目地用到三角形全等中。实际上，三角形全等的判定方法只有“SAS”“ASA”“AAS”“SSS”“HL”，此题不能利用等式的性质直接求解。

【正解】在△AOD和△BOC中，

∵∠A=∠B，∠AOD=∠BOC，AD=BC，

∴△AOD≌△BOC（AAS）。

四、生造条件参与证明出错

例4如图4，在△ABC中，AD是它的角平分线，BD=CD，DE、DF分别垂直于AB、AC，垂足为E、F。求证：BE=CF。

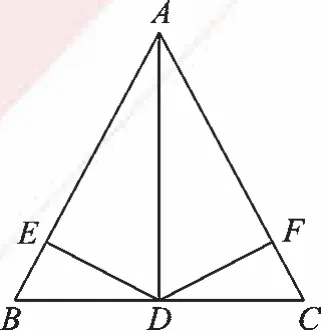
图4

【错解一】由图可知DE=DF，

在Rt△BDE与Rt△CDF中，∵DE=DF，BD=CD，∴Rt△BDE≌Rt△CDF（HL）。

∴BE=CF（全等三角形的对应边相等）。

【错解二】由图可知AD⊥BC，通过证明△ABD≌△ACD，得AB=AC。再由Rt△AED≌Rt△AFD，得AE=AF，从而得到BE=CF。

【知错】证明过程必须要有根有据。根是题目的已知条件；据是证题的依据，即书上的公理、定理、定义等，不能想要什么条件就写什么条件。错解一中认为DE=DF，并没有经过证明，就直接作为已知条件应用，因而产生错误；错解二中，把AD⊥BC当作条件，没有经过证明，因而也产生错误。产生上述错误的原因是证题不严谨，推理过程不符合全等三角形的判定方法。

【正解】∵AD是△ABC的角平分线，

∴∠BAD=∠CAD，DE=DF（角平分线上的点到角的两边的距离相等）。

∵DE、DF分别垂直于AB、AC，∴∠AED=∠AFD。又∵AD=AD，∴△DAE≌△DAF。

在Rt△BDE与Rt△CDF中，∵BD=CD，DE=DF，∴Rt△BDE≌Rt△CDF（HL）。

∴BE=CF（全等三角形的对应边相等）。

五、思考不全面出错

例5 如图5所示，在等边△ABC中，D、E、F分别为AB、BC、CA上一点（不是中点），且AD=BE=CF，若将几个全等的三角形看作一类，则图中全等三角形有（ ）类。

图5

A.3 B.4 C.5 D.6

【错解】A。

【知错】部分同学审题时过于简单，不细心推敲，没有灵活运用所给条件，再推出新的结论，只是直接运用了已知条件就做出简单判断。

【正解】∵AB=AC=BC，AD=BE=CF，∠BAC=∠ABC=∠ACB，∴△EBA≌△DAC≌△FCB。

∵BD=AF=EC，AB=AC=BC，∠BAC=∠ABC=∠ACB，∴△DBC≌△FAB≌△ECA。

∵∠BAE=∠ACD=∠CBF，AD=BE=CF，∠AEB=∠ADC=∠BFC，∴△ADG≌△CFN≌△BEM。

∵ ∠ABM=∠CAE=∠BCD， AB=AC=BC，BM=AG=CN，∴△ABM≌△ACG≌△CBN。

∵∠AGD=∠EGC，∠FNC=∠DNB，∠BME=∠AMF， ∠AGD=∠FNC=∠BME， ∴ ∠EGC=∠DNB=∠AMF。∵BD=AF=EC，∠DBN=∠FAM=∠ECG，∴△DBN≌△FAM≌△ECG。故选C。

同学们可以通过对全等三角形易错题的研究，寻找错误的原因，采取相应的纠正方法，在改正错题的过程中掌握数学知识，积累解题经验，提高解题能力。