“三象一作”认知方法下的数学概念教学——以“认识平均分”为例

钱艳妮 孙晓华

摘要：“三象一作”（现象、心象、抽象、操作）的数学认知过程（方法）对于小学数学教学具有理论指导意义及可操作性。教师可以遵循这一认知过程，有意识地鼓励、引导学生搜集、观察身边的数学现象，再通过多种策略帮助学生在头脑中形成科学规范的心智图像，最后通过层层抽象帮助学生完成知识的建构。教学“认识平均分”时，注意创设现象情境，着力于多种分法形象的积累;激活心智图像，着力于平均分内涵的清晰;进行数学抽象，着力于平均分概念的形成;开展操作活动，着力于平均分本质的深化。

关键词：三象一作数学概念教学认识平均分

王名扬老师和徐沥泉老师、徐利治先生在《论一种缘自认知心理学及教育学研究的数学认知过程》一文中提出“三象一作”（现象、心象、抽象、操作）的数学认知过程。这一认知过程（方法）对于小学数学教学具有理论指导意义及可操作性。在日常教学实践中，我们遵循这一认知过程，有意识地鼓励、引导学生搜集、观察身边的数学现象，再通过多种策略帮助学生在头脑中形成科学规范的心智图像，最后通过层层抽象帮助学生完成知识的建构。下面，以苏教版小学数学二年级上册“认识平均分”的教学为例，谈谈具体的做法。

一、创设现象情境：着力于多种分法形象的积累

数学是研究数学现象的科学。数学现象是数学形式化题材的生命之源，也是学生心智图像形成的客观背景。生活中存在着大量的数学现象，我们可以由此创设教学情境。

在教学“平均分”时，教师首先要从平均分的知识和学生已有的认知经验出发，呈现有效的数学现象，引入平均分的概念。综合平均分知识的生长线索和低年级学生的认识特点考虑，在呈现有关平均分的数学现象时，要紧扣趣味性、多样性等特征，引导学生搜集分法的现象，帮助学生积累多种不同分法的形象。

（一）引入生动有趣的数学现象

华罗庚先生说过：“人们对数学早就产生了枯燥乏味、神秘难懂的印象，原因之一便是脱离了实际。”因此，依据学生熟悉的实际生活创设教学情境，让学生发现生活中的数学现象，激发学习数学的兴趣，就显得尤为重要了。

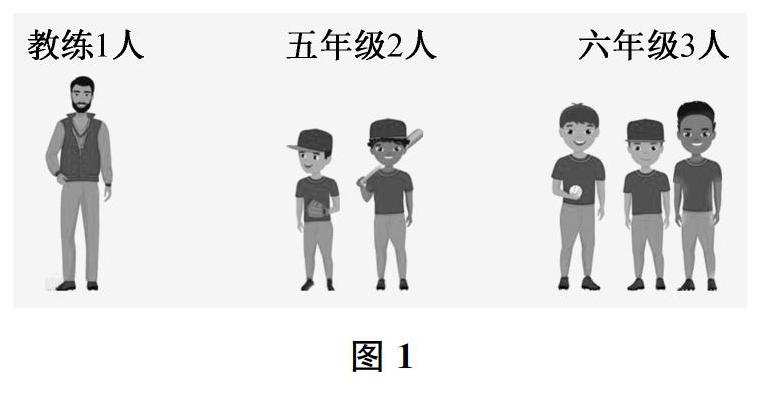
课始，教师向学生呈现“学校棒球队9月份去台湾参加‘海峡杯比赛，夺得了金灿灿的冠军奖杯。他们凯旋的那天正好是中秋节，学校给他们送来了月饼”的场景，提出“每组6人（教练员1人、五年级队员2人、六年级队员3人，如图1）领到6个月饼，可以怎样分”的问题。这一问题情境迅速引发了学生参与思考的热情和欲望。透过这一现象，学生可以真切地感受到“怎样分物品”是现实生活中需要解决的问题。

（二）积累丰富多彩的数学形象

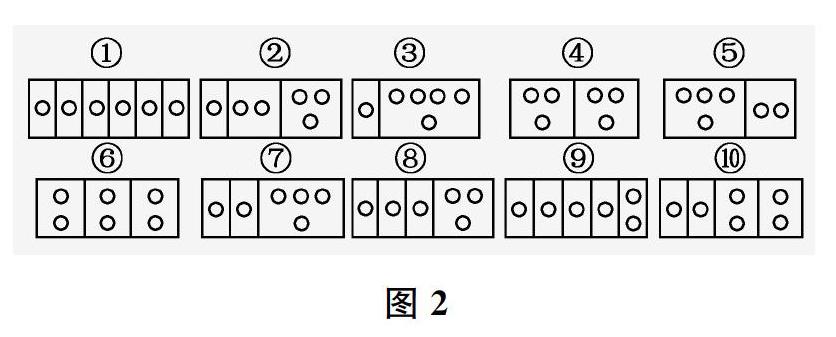
之后，教师根据图1，引导学生思考如何分。从图片信息出发，学生自然地想到了两种分法：①把6个月饼分成6份，每人1个;②把6个月饼分成3份，分别是1个、2个和3个。教师启发：能不能从教练员和队员两类考虑？这一问题又诱发出如下分法：③把6个月饼分成2份，教练员作为1份（1个），五、六年级队员合起来作为1份（5个）。受此启发，许多学生认为还可以有如下方法：④教练员与五年级队員合起来作为1份（3个），六年级队员作为1份（3个）;⑤教练员与六年级队员合起来作为1份（4个），五年级队员作为1份（2个）。至此，学生的思路更加开阔，还想到如下分法：⑥教练员与六年级的1个队员合起来作为1份（2个），六年级剩下的队员作为1份（2个），五年级队员作为1份（2个）;⑦五年级队员作为2份（2个），教练员与六年级队员合起来作为1份（4个）;⑧六年级队员作为3份（3个），教练员和五年级队员合起来作为1份（3个）;⑨教练员与六年级队员作为4份（4个），五年级队员作为1份（2个）;⑩教练员与六年级的1个队员作为2份（2个），六年级剩下的队员作为1份（2个），五年级队员作为1份（2个）。而后，教师把学生的这几种分法汇集起来进行板书（如图2）。

可以看到，学生创设的多种不同的分法都是具有现实意义的，都是数学现象。学生在创设的过程中情绪是高涨的，思维是活跃的。更重要的是，这些数学现象蕴含了平均分知识的线索和内涵，为学生心智图像的形成奠定了基础。

二、激活心智图像：着力于平均分内涵的清晰

“心智图像是数学现象在人们心目中呈现的一类未经理性分析的直觉形象，是人们对数学现象的某种直接的领悟和图像。”数学现象是对数学内涵的呈现，心智图像则是对数学内涵的二次呈现。心智图像具有一定的概括性，由此也就有了不同的迁移能力。数学学习中，并非概括水平越高的心智图像越有利于理解，而是在不同的阶段需要相应水平的心智图像。数学教学中，引导建构的心智图像必须能够反映数学的本质，因为不管形成怎样的心智图像，目的都是帮助学生理解数学。

“平均分”是除法知识中一个重要的起始概念。为了帮助学生建构有效的心智图像，获得较为清晰的认知图式，教师在教学中预设形成以下心智图像：

第一，教师引导学生观察比较多种不同的分法（图2），要求学生努力发现哪些分法有共同的特点。经过讨论，师生得到两种不同的分类（如图3）：一是每份分得同样多的，二是每份分得不同样多的。这一心智图像的形成让学生顺利从多种不同的分法过渡到两种不同的类别，有助于学生在对比中凸显对“每份分得是否同样多”特点的感悟。

第二，教师引导学生观察比较每份分得同样多的3种分法（图3中的第一类），再按每份分得的个数多少进行有序排列（如图4）。这种心智图像的形成让学生对“同样多”的含义具体化，从中领悟到“同样多”也是可以有多种不同的样式的，使“同样多”的内涵得到丰富。

三、进行数学抽象：着力于平均分概念的形成

学生对数学现象形成了未经理性分析的直觉形象后，还需要进一步通过心象的丰富、变化、组合、联结等过程，形成概括性的抽象概念。

在这一环节，教师开展如下三个层次的教学。

（一） 横向比较归纳——运用数学语言表达平均分的意义

借助图3，教师提问：为什么把①号、④号、⑥号分法分在第一类，把其余分法分在第二类呢？学生回答：第一类的3种分法与第二类的7种分法有不一样的特点。教师追问：第一类的分法与第二类的分法分别有什么不同的特点呢？学生回答：第一类每种分法中的每份都是同样多的，第二类每种分法中的每份都是不同样多的。教师板书：每份分得同样多。这样，从事物的具体背景中把一类事物的本质特征抽取出来。而后，教师揭示平均分的名称。

（二） 纵向比较归纳并举例——丰满平均分的意义

师（指图4）这三种分法有个简洁的新名字，你知道是什么吗？

生平均分。

师为什么？

生因为它们分得一样多。

生因为在它的每种分法中，每份分得都是同样多的。

师这位同学说得真好！那么，（指图4中的排列一）观察这三种分法，它们又有什么不同点呢？

生第一种每份都是1个，第二种每份都是2个，第三种每份都是3个。

师说得好！同样是平均分，即每份分得同样多，也是可以有多种不同的样式的。你能说说实际生活中还有哪些不同的样式吗？

生写5行字，每行4个。

生我们教室里有8排学生，每排都是5人。

生电脑教室里有8张电脑桌，每张桌上有6台电脑。

……

（三） 顺向判断，逆向索因——加深平均分意义的理解

教师出示图5，让学生判断哪种分法是平均分，并要求学生说清楚判断的理由，然后提出如下问题：如果把这9个球平均分成3份，每份之间应该怎样移补？如果平均分成3份，每份是2个，球的总数应该是几个？需要去掉几个？如果平均分成3份，每份是5个，球的总数又应该是几个？需要添上几个？经过这样先顺向判断，后逆向索因的思维活动，学生更能充分地理解平均分的意义，完整地建构平均分的概念了。

四、开展操作活动：着力于平均分本质的深化

所谓“操作阶段”，就是对知识不断运用和不断“再认识”“再提升”的阶段。这一阶段“就是在合乎逻辑法则的条件下，操作运用抽象的数学知识与数学方法（包括数学符号和数学语言的运用），去处理数学问题并进一步去发展数学理论知识”。

教學中，教师通过以下两个层次的操作活动，让学生发现新知识，加深对平均分意义和特点的认识。

（一）多题归一

题组（1）有8个苹果，每个小朋友分2个，可以分给几个小朋友？

8个，每人分2个，可以分给（）人。

（2）圈一圈，填一填。

9块，每（）块一份，分成了（）份。

（3）圈一圈，填一填。

（）个，每5个一份，分成了（）份。

由于学生初次运用平均分概念解决实际问题，针对第（1）题，教师提示学生“每个小朋友分2个，也就是2个2个地分”;针对第（2）、第（3）题，教师提醒学生运用圈一圈的方法。学生完成后，教师提问：这三道题的分法有什么不同？有什么相同之处？在比较、分析、归纳中，学生感悟到：虽然平均分被赋予了不同的生活元素，但是剔除非本质的因素，不管是把8个苹果每2个一份地分，还是把9块橡皮每3块一份地分，或者把15个笔套每5个一份地分，都是每份分得同样多。

（二）一题多变

题1先用12支铅笔分一分，再填空。

（1）每1支一份，可以分成（）份。

（2）每2支一份，可以分成（）份。

（3）每3支一份，可以分成（）份。

教学时，教师先让学生操作分法，并根据学生的反馈汇总成表格（如表1）。接着，引导学生观察、比较、分析：①要分的12支铅笔与每份的支数及分成的份数有什么关系？（1×12=12，2×6=12，3×4=12）②根据上述关系，你能猜一猜12支铅笔还可以每几支一份地分，分成的份数是多少吗？（每4支一份，分成3份;每6支一份，分成2份）然后，根据学生的猜想，用操作进行验证。之后，引导学生思考：从上往下看，每份的支数怎样变化？分成的份数呢？从下往上看呢？学生通过观察、比较、推想，发现把总数平均分之后，总数、每份数、份数之间存在的特定关系，从而感悟到不管每份的支数与分成的份数怎样变化，它们相乘的结果即总数是不变的，由此渗透了变化与对应的思想。

师（利用多媒体课件，动态演示“把15个气球每人3个，发给排在前面的2人”）照这样分一分，15个气球可以分给几个小朋友？

生可以分给5个小朋友。

师你是怎样想的？

生顺着次序分给小朋友，3个一份地分，分5份，正好分完。

生我想用减法：分给一个小朋友就减去一个3，依次用15-3-3-3-3-3=0，减5次是0，说明正好分完，所以可以分给5个小朋友。

生我直接想5个3是15，所以分给了5个小朋友。

（教师出示如下变式问题，让学生看图填空。）

15个，每人分3个，可以分5人。

（）个，每人分3个，可以分（）人。

（）个，每人分3个，可以分（）人。

（）个，每人分3个，可以分（）人。

师你还能依次想到把几个气球每人分3个，分给几个人呢？

生27个气球分给9个人，30个气球分给10个人，33个气球分给11个人。

师照这样的规律往下想，说得完吗？

生说不完，有很多很多这样的数。

对于此题，教师同样没有因为获得解答结果而止步，而是引导学生进行更高层次的思维爬坡，让学生通过观察、比较和推想，知道符合上述规律的总个数和可以分给的人数都有无穷个，再一次感受到两个量之间的变化与对应关系。

参考文献：

[1] 王名扬，徐沥泉，徐利治.论一种缘自认知心理学及教育学研究的数学认知过程[J].数学教育学报，2013（1）.

[2] 张洪魏.关于学生数学认知理解的思考[J].数学教育学报，2006（4）.

[3] 顾丽英，许光新.例谈“三象一作”教学模式的实施策略[J].教学月刊（小学版），2014（10）.

[4] 史宁中.学科核心素养的培养与教学——以数学学科核心素养为例[J].中小学管理，2017（1）.