轴承自旋运动的分析
2019-10-21 09:41
福建质量管理 2019年19期
(天津工业大学机械工程学院 天津 300387)
一、轴承的运动分析
球轴承中,滚珠的运动形式十分复杂,不仅有绕轴承轴线的公转,同时还有绕自身轴线的自转运动。当接触角大于零时,即对于角接触球轴承,滚珠还会产生相对滚道的自旋运动以及由于陀螺力矩导致的陀螺旋转。高速轻载时,轴承中还可能出现公转打滑现象。因此,高速轴承,尤其是高速角接触球轴承的运动学计算,需要通过建立相应(但复杂)的运动方程求解滚动体的运动。
假设滚珠的中心固定在空间中,轴承的内圈以ωi的角速度进行旋转,内圈与滚动体产生的接触椭圆在内圈滚道上最多出现两个纯滚动点,把出现纯滚动点的半径记为ri,如图1所示。

从图中可以推导出滚珠和内滚道在接触椭圆短轴方向的滑动速度
滚珠和内滚道在接触椭圆长轴方向的滑动速度

滚珠相对于内滚道的滑动速度

同样对于外滚道与滚珠的接触可以推导出滚珠和外滚道在接触椭圆短轴方向的滑动速度
滚珠和外滚道在接触椭圆长轴方向的滑动速度
cosβsinβ′
滚珠相对于外滚道的滑动速度

若采用外滚道控制理论,即假设滚珠在即假设滚珠在外滚道上发生纯滚动无自旋,可使计算简化。同时,由于轴承使用中应防止陀螺旋转的发生,故在忽略陀螺运动情况下,对于外圈固定、内圈旋转的轴承,滚珠公转角速度、自转角速度及相对于内滚道的自旋角速度的计算公式分别为
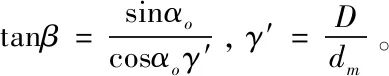
本文中218角接触球轴承为例对轴承运动进行了计算,轴承的具体参数如表1所示以及运用matlab对上述公式进行求解,求得的结果如表2所示。

表1 轴承参数

表2 轴承运动学分析结果
二、结论
(1)相同载荷时,轴承的自旋速度随着转速的增加而增加,并且通过数据可以得之自旋速度增长的速率在降低。(2)相同转速时,随着载荷的增加轴承的自旋速度是降低的,这是因为轴向载荷的增加导致滚珠与内外圈之间的摩擦增大,因此自旋速度会降低。
猜你喜欢
哈尔滨轴承(2021年4期)2021-03-08
制造技术与机床(2019年11期)2019-12-04
制造技术与机床(2019年6期)2019-06-25
华东理工大学学报(自然科学版)(2017年5期)2017-11-01
中学生数理化·高一版(2017年3期)2017-07-08
制造技术与机床(2017年4期)2017-06-22
通信电源技术(2016年1期)2016-04-16
火控雷达技术(2016年1期)2016-02-06
海军航空大学学报(2015年1期)2015-11-11
中国铁道科学(2015年4期)2015-06-21

