为发展学科一般观念而教——兼谈解析几何复习起始课教学

李昌官

(浙江省台州市教育局教研室 318000)

1 何为学科一般观念

本文把解析几何、立体几何、概率统计等相对独立的数学分支也视为学科.学科一般观念是指对本学科学习和研究具有广泛、持久、深刻影响的基本数学思想方法和基本思维策略方法.从学习与掌握视角看，学科一般观念具有直观、简明、易懂但难深入等特点；从功能与价值视角看，它具有统摄性、一般性、普适性强等特点.如解析几何中的坐标法、借助方程研究几何图形的性质、运动变化观点等，都属于学科一般观念的范畴.

2 为何要发展学科一般观念

学科一般观念是学好本学科的基础和关键.因为它是学科的核心与灵魂，是学科成长和发展的基石；它为如何构建本学科知识、提出问题和解决问题提供思维的方向与策略；离开了一般观念的引领和组织，该学科的学习将变得松散、零碎、低效、缺少灵性和活力.

学科一般观念是解决本学科问题的金钥匙.“数学教学的根本任务是发展学生的思维能力，说到底就是要使学生在面对问题时总能想到办法.注重一般观念的思维引领作用，可以提高思维的系统性、结构性，有效克服‘做得到但想不到’的尴尬，使数学的发现更具‘必然性’”[1]780.学科一般观念的特点决定了它对本学科问题的解决具有很强的引领与指导功能，数学应有意识地培养学生“从基本概念、基本原理及其联系性出发思考和解决问题的习惯”[1]737.这既是提高学生应试能力的大道和王道，也是发展学生思维能力的大道和王道.

发展学科一般观念是提升核心素养的需要.学科核心素养是学科知识、技能遗忘后留余下来的并持续发挥作用的东西.“数学的本质是不断抛弃较特殊的概念，寻求较一般的概念；抛弃特殊的方法，寻求一般的方法.”[2]数学教育的目标不仅在于数学概念、数学定理的积累，更在于形成这些概念和定理背后蕴含的一般观念、一般方法和学科品性.

3 如何发展学科一般观念

为了有效地发展学生的学科一般观念，可采取如下教学策略.

3.1 追根溯源，揭示学科一般观念产生的背景、过程与方法

学科一般观念不可能在真空中产生，它需要一定的土壤、环境与温度，并且必然有一个萌芽、孕育、生长、发展、成熟的过程.揭示学科一般观念产生的背景、过程与方法，有助于解决抽象观念与具体情境的脱节问题，有助于学生更深刻、更全面地理解一般观念.以解析几何复习起始课教学为例,应揭示解析几何的产生是为了使直观形象的“形”能借助抽象精确的“数”进行计算，其源头是坐标平面上的点与有序数对的一一对应；应揭示和梳理解析几何形成与发展的轨迹(具体可参见后面的图5)；应剔除不必要的细节内容，突出和强调一般观念，帮助学生形成具有广泛应用性和深远影响的解析几何问题的研究思路与研究方法.

3.2 “虚”“实”结合，用“虚”指导“实”，又从“实”中提炼“虚”

这里的“实”是指知识、技能、题目等容易触摸的东西；“虚”是指思想、观念、策略等难以把握的东西.应处理好认识“森林”与认识“树木”的关系，寻找“实”的东西背后所蕴含的“虚”的东西：既先见森林、后见树木，又善于通过树木来认识森林.应切记：“一般观念是将特殊结果联系起来的手段.毕竟，具体的特殊事物才是重要的.因此，在你对事物进行数学处理时，结果无论多具体也不为过，方法无论多一般也不为过”[3]29.以解析几何复习起始课教学为例,一方面，应在解析几何一般观念的指导和引领下，探寻解析几何的源头，探究发现曲线的性质，解决包括数学高考题在内的数学问题；另一方面，应通过相关知识的学习、相应问题的解决来提炼解析几何一般观念，深化学生对它们的认识.更进一步，解析几何复习起始课解题教学的目的主要不在解题本身，而在于通过解题来说明解析几何的学习目标与考试要求，强化解析几何解决问题的一般思路与一般方法；是“抓住为数不多的阐明整体的一般观念，持久稳定地汇集所有相关的辅助事实”[3]48.

3.3 注重整体，抓“大”放“小”，避免被繁杂的细节所干扰

“如果你深入到细节中去，你就可能在细节中迷失自我.过多过细的枝节对思维是一种负担.它们会阻碍你对要点投入足够的注意力，甚至会使你全然看不到要点”[4].对解析几何复习起始课而言，应重在明晰课程标准与考试大纲关于解析几何考查的原则性、框架性要求，而不是数学高考中解析几何的题型分布与知识点分布；应重在解决一般性、框架性、策略性问题，而不是具体的细节问题；应重在用解析几何的一般观念把前面所学的内容串联起来，使之形成一个统一的整体，而不是关注某类问题的特定解法；应重在解决学生解析几何学习中存在的普遍性、全局性问题(如学习习惯、学习方法问题)，而不是解决特定知识点学习中存在的问题.也就是说，复习起始课应强化整体把握、整体指导，为学生后续复习提供包括复习目标、复习方法、复习路径、一般观念等在内的先行组织者.

3.4 强化感悟，尤其是学生的自我感悟和综合感知

陈述性知识的学习主要靠传授，程序性知识的掌握主要靠训练，策略性知识、观念性知识的形成主要靠教师指导基础上的学生自我实践、自我感悟与自我内化.因为没有学生的亲身实践和自我感悟作基础的“一般观念”是脱离情境的、抽象的、空洞的言语信息，是难以迁移、难以用于解决问题的他人的一般观念.另外，由于学科一般观念具有很强的整体性、结构性和综合性，因此应通过综合感知、整体感知，使学生“对隐藏于数学对象深层的数学事物关系间的和谐性与规律性有深切感受，对隐藏于数学知识间的逻辑脉络和演绎方式有深切感受”[5].

4 为发展学科一般观念而教之案例——解析几何复习起始课教学

4.1 解析几何课程目标与考试目标

尽管解析几何的课程目标与考试目标远不是一节复习起始课所能达成的，但它们仍然是制定复习起始课教学目标的重要依据.《普通高中数学课程标准(2017年版)》指出，解析几何的课程目标是“在平面直角坐标系中，认识直线、圆、椭圆、抛物线、双曲线的几何特征，建立它们的标准方程；运用代数方法进一步认识圆锥曲线的性质以及它们的位置关系；运用平面解析几何方法解决简单的数学问题和实际问题，感悟解析几何中蕴含的数学思想”；解析几何的学业要求是“能够掌握平面解析几何解决问题的基本过程：根据具体问题情境的特点，建立平面直角坐标系；根据几何问题和图形的特点，用代数语言把几何问题转化成为代数问题；根据对几何问题(图形)的分析，探索解决问题的思路；运用代数方法解决问题得到结论；给出代数结论合理的几何解释，解决几何问题.能够根据不同的情境，建立平面直线和圆的方程，建立椭圆、抛物线、双曲线的标准方程，能运用代数的方法研究上述曲线之间的基本关系，能运用平面解析几何的思想解决一些简单的实际问题”[6].

由上不难发现，无论是解析几何的课程目标还是学业要求，它们的根基和核心都是坐标法，需要解决的问题都是曲线的性质及其位置关系方面的，解决的基本思路都是借助方程对曲线进行计算.因此解析几何复习教学应该突出和强化一般观念，突出和强化一般观念与具体解题之间的联系；应在一般观念的指导下解决具体问题，同时在具体问题解决的过程中提炼、强化一般能力和一般观念.

4.2 学生解析几何方面的认知基础与认知缺陷

通过解析几何新课学习，学生对解析几何的基本概念、基本思想、基本技能有一定的了解、理解或掌握，但他们的学习明显存在如下问题：一是重具体技能而轻一般观念，对解析几何的学科意义、学科价值、基本思想认识不到位，以至于许多学生面对高考题——教材中“坐标平面上的直线”与“圆锥曲线”两章内容体现出解析几何的本质是什么——时不知所措，答分率低下；二是重知识积累，而轻知识梳理，他们学到的往往是孤立的、碎片化的知识，而不是作为整体的一部分、相互联系的知识；三是重知识是什么，而轻知识为什么是这样，他们对知识的掌握往往停留在记忆、理解和运用的水平上，而达不到分析、评价与创造的水平；四是解题重数量而轻质量，他们往往为完成教师布置的任务而解题，盲目解题、机械解题、“入宝山而空返”现象严重.笔者曾对台州市30000多的高三学生进行问卷调查，结果表明：从高一到高三，学生的学习习惯、解题习惯不仅没有得到优化，反而是恶化.

4.3 解析几何复习起始课的教学功能与教学目标

4.3.1复习起始课的教学功能

复习起始课与新课起始课的环境与条件不同：新课起始课学生缺乏相应的经验与感受，教师难以为学生提供清晰的学习框架，而复习起始课则不同；新课起始课学生还没有暴露出学习的问题与不足，教师只能凭经验进行教学，而复习起始课则可基于对学生前期学习情况的调查与检测、针对学生存在的问题与不足进行教学.复习起始课的教学功能与新课起始课的教学功能既有共同点，也有不同点.其共同点都是为后继学习提供先行组织者；都不是重在解决具体细节问题，而是重在解决一些整体性、框架性、一般性问题.其不同点在于：新课起始课重在孕育一般观念，而复习起始课重在强化一般观念；新课起始课重在搭建学习框架与知识框架，而复习起始课重在梳理和完善已经初步形成的知识框架.从学习心理看，新课学习时教师和学生都难免被新的东西所吸引，进而把注意力放在新的情境、新的知识、新的技能上，放在对特定问题的认识和解决上，而复习起始课则有条件跳出具体知识和解决问题的细节，在更一般、更宽广的视角下重视审视所学知识，以更好地形成学科一般观念，掌握学科基本方法.

4.3.2解析几何复习起始课的教学目标

根据解析几何的课程目标与学业要求，根据学生的认知基础，针对学生前期学习中暴露出来的问题，制定解析几何复习起始课教学目标如下：

(1)能在具体情境和解决问题的过程中，感受解析几何的孕育与发展，深化对解析几何本质的认识，明晰解析几何解决问题的一般思路与一般方法，强化解析几何的一般观念，欣赏解析几何的价值；

(2)在对解析几何高考题的分析与梳理中，明晰解析几何高考的主要内容与考查目标，感知解析几何高考的基本要求；

(3)能反思解析几何新课学习中存在的问题与不足，有弥补这些不足、优化自己的学习习惯与学习方法的意识与行为.

4.4 解析几何复习起始课的教学过程

4.4.1回顾检测，暴露问题，明确目标

回顾与检测1你能判断图1(1)中点P1与P2是否关于y轴对称吗？能判断图1(2)中点O、A、B、C是否共线吗？如果已知点A、B、C的坐标分别为(3，8)，(5，13)，(8，21)(如图1(3))呢？

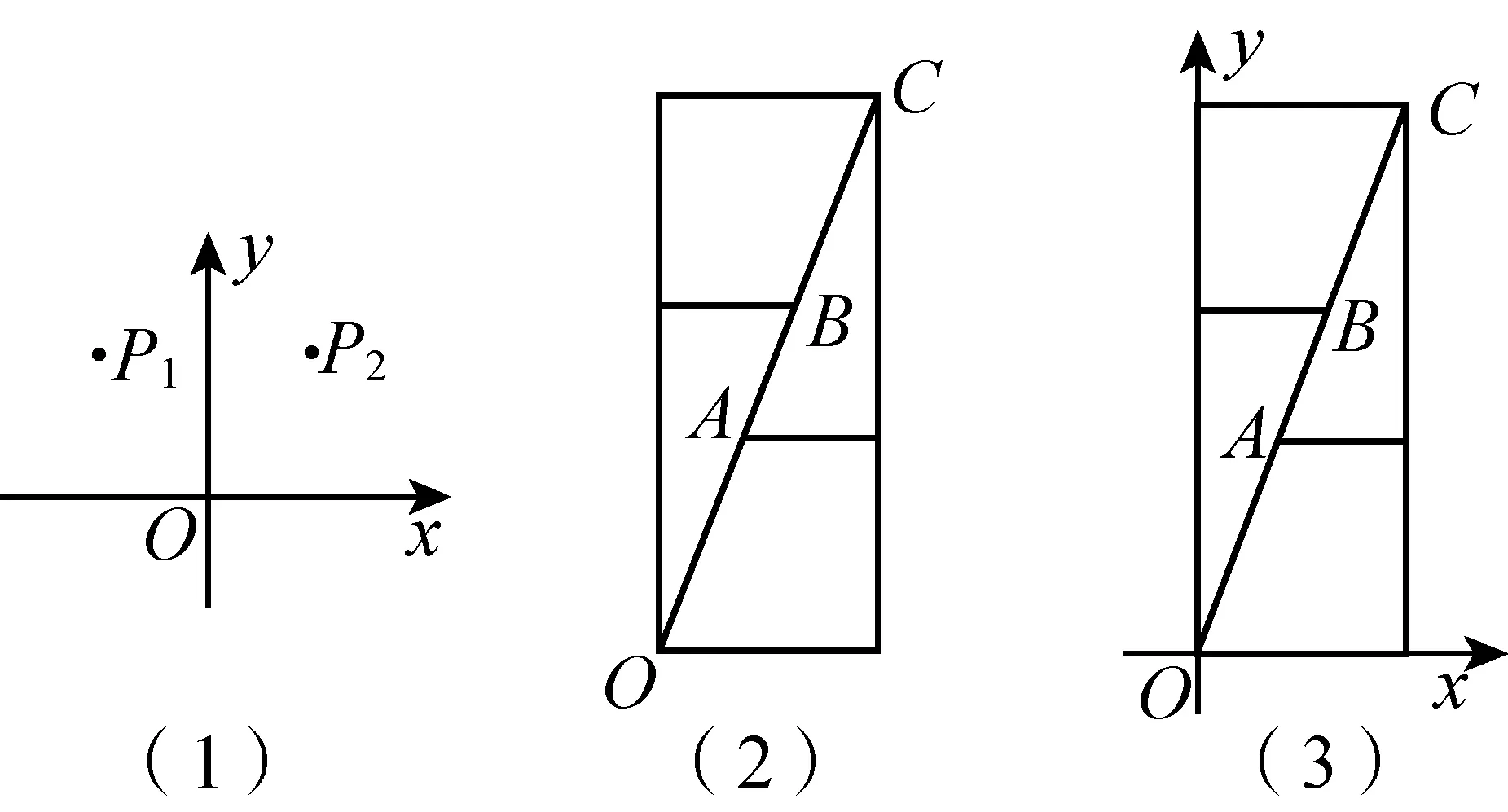
图1

【设计说明】(1)目的是了解学生对解析几何特点与优点的认识；(2)对图1(1)，可先让学生充分发表自己的看法，猜想结果，然后教师借助数学软件显示这两点的坐标；(3)让学生认识到：几何具有形象直观的优点，但也有不便计算和难以精确刻画的缺点，解析几何用坐标表示点、用方程表示曲线，正是为了使图形能够借助坐标和方程进行运算，进而使数学同时具有“数”与“形”的优势.

回顾与检测2解析几何为什么能够通过方程研究曲线？“曲线与方程”和“点与有序数对的一一对应”有怎样的联系？

【设计说明】(1)目的是了解学生对解析几何基本思想理解的深刻程度.(2)解析几何的源头是点与有序数对的一一对应关系，其基本思想有两个基本要点：一是坐标法；二是运动变化观点.在解析几何中，曲线被看作点运动所成的轨迹，方程被看作有序数对变化时所满足的条件.正是在这种运动变化中，点与有序数对始终保持一一对应关系，因此人们能够通过方程来研究曲线.(3)在学生讨论的基础上，出示2004年上海数学高考题——教材中“坐标平面上的直线”与“圆锥曲线”两章内容体现出解析几何的本质是什么？强化学生对解析几何本质及其重要性的认识.

回顾与检测3下列是2018年全国卷Ⅰ理科解析几何部分的高考题，它们涉及哪些曲线和曲线的哪些性质？所用的基本思路与基本方法是什么？

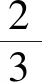
A.5 B.6 C.7 D.8

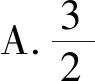
①当l与x轴垂直时，求直线AM的方程；

②设O为坐标原点，证明：∠OMA=∠OMB.

【设计说明】(1)呈现最新的高考真题，目的一是为了了解学生看待高考题的角度；二是为了让学生了解解析几何高考的基本现状和主要内容；三是为了以之为载体，说明解析几何高考考查的基本问题及所用的基本思路与基本方法，为后继复习指明方向.(2)分析时，不关注考查具体的知识点，也不关注具体的解题细节，只关注试题所对应的基本问题以及解决所用的基本思路与方法.(3)分析发现：考查所涉及的曲线包括直线、椭圆、双曲线、抛物线等，所要解决的是它们的位置关系和度量大小问题，所用的基本思路与方法是先求相应曲线的方程，然后借助方程来解决问题.

【回顾与检测1-3设计总说明】直面解析几何的学科本质和高三学习的主要任务，揭示解析几何发展的内在逻辑，深化解析几何的一般观念，同时尽最大可能暴露学生前期学习中存在的问题与不足，为学生后续复习指明目标与方向.

4.4.2实战演练，强基固本，提升能力

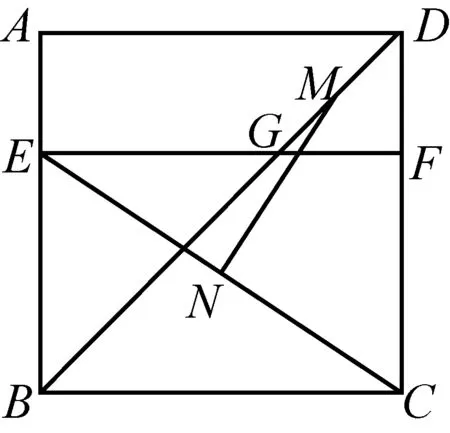
图2

问题1(2017年浙江宁波中考第11题)如图2，四边形ABCD是边长为6的正方形，点E在边AB上，BE=4，过点E作EF∥BC，分别交BD，CD于G，F两点.若M，N分别是DG，CE的中点，求MN的长.

【设计说明】(1)距离是几何的核心概念，是解析几何应用的重要方面.(2)在没有呈现解析几何背景的情况下，引导学生自觉地利用坐标法加以解决几何问题.(3)深化学生对运用坐标法解决问题的思路、方法与价值的认识.

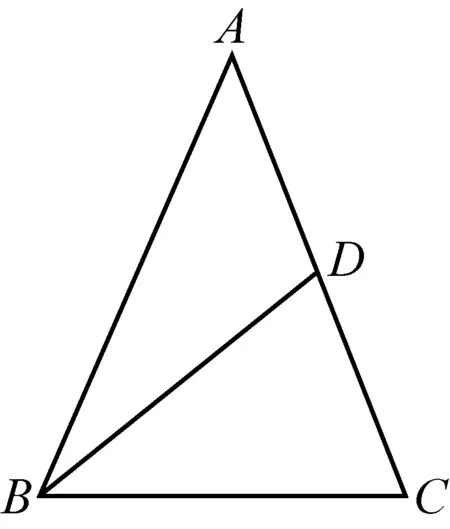
图3

问题2如图3，已知△ABC为等腰三角形，AB=AC，D是AC的中点，且BD=3，求△ABC面积的最大值.

分析：(1)首先应从运动与变化的视角看待问题.(2)考虑到此问题是最值问题，故可从函数角度切入.为此，只要把S△ABC用某个变量的解析式表示.(3)考虑到已知BD=3，故可把B，D看作定点，把A，C看作动点.由D是AC的中点，知S△ABD=S△BCD，故可通过求点A的轨迹方程来求S△ABC的最大值.

【设计说明】问题2与问题1一脉相承，学生面对的都是没有解析几何背景、真实的平面几何问题，但问题1只用坐标法就能解决，而问题2要通过建立方程、研究方程才能解决，因此问题2更利于发展学生运用解析几何基本思想解决问题的能力.

问题3前面回顾与检测3的第(2)题.

【设计说明】(1)运用高考真题激发和调动学生的积极性，同时借此进一步揭示高考考查的基本问题与基本方法.(2)对解析几何运算，指导学生先理解运算对象、明确运算目标、分析运算条件、探寻运算思路、确定运算方法，避免盲目地、无章法地计算.(3)强化解析几何解题的另一个一般观念——充分利用图形的几何性质来简化计算；对选择题、填空题，尤其应做到“小题小作”，而不是“小题大做”.如图4，应能意识到∠MOF=∠NOF=∠ONF=30°.

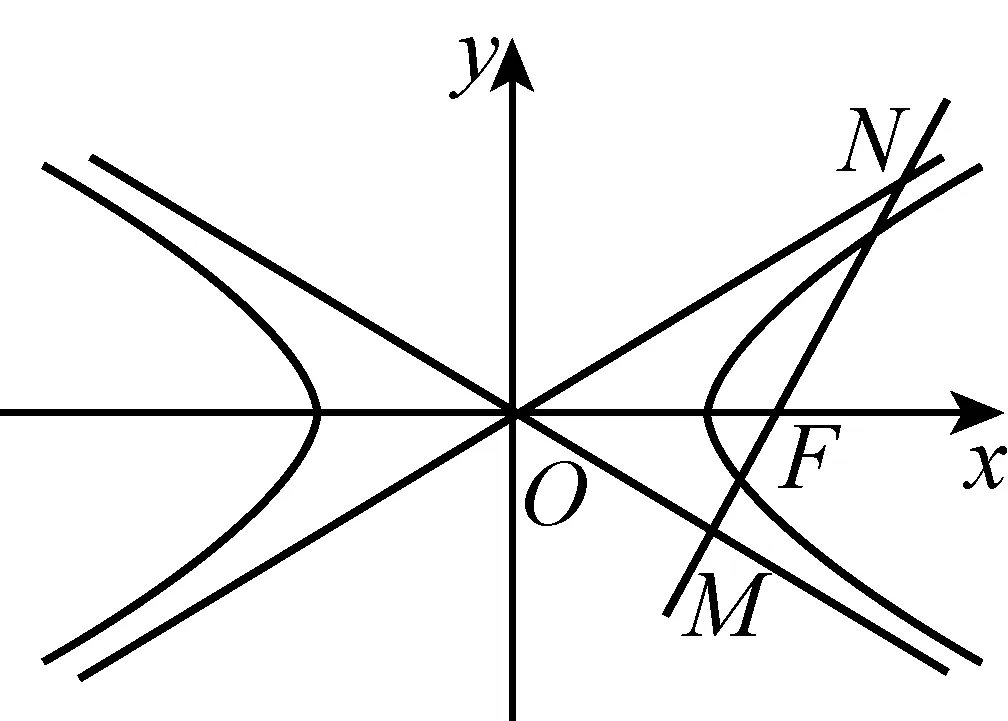
图4

【问题1-3设计总说明】(1)这3个问题均先学生独立思考，然后学生相互讨论，最后教师点评、讲解.如果学生相互讨论仍不能解决问题，那么教师提前作启发性、引导性点拨.(2)强化解析几何一般观念与具体问题解决的相互促进.(3)问题解决后，应强化学生的自我反思与自我感悟，为学生内化解题策略、深化一般观念留出时间和空间.

4.4.3回顾反思，梳理结构，指导学法

(1)学生回顾、反思本节课的学习，进一步感悟和内化解析几何一般观念，同时注意寻找自身学习存在的问题与不足.

(2)教师按图5梳理解析几何的结构体系与高考重点.

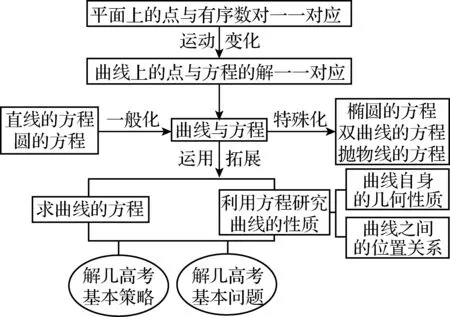
图5

(3)学法指导.提醒学生在解析几何复习中注意如下几点：第一，把握利用方程研究曲线性质这一根本性的学科特点与思维方式；第二，分析题目条件与条件之间、条件与结论之间的联系，弄清楚为何一件事成为另一件事发生的依据，并意识到这是思维的核心与关键；第三，伤其十指，不如断其一指，应加强解题后的回顾与反思，做到举一反三、触类旁通，提高解题效益；第四，解析几何运算应重算理、优算法、不怕繁，应把运算作为优化自己个性品性的载体与平台.

5 结束语

数学教学应基于“四基”，发展“四能”，孕育数学核心素养；应基于学科知识提炼凝聚学科观念，孕育发展学科品性.即便是高三复习教学，也应通过发展思维能力和学科一般观念来提升考试成绩，做到“育分”与“育人”双丰收.