数字工具支持下数学建模的研究综述

钱月凤

(苏州大学数学科学学院 215006)

近年来，由于信息技术的迅猛发展，数字工具在数学课堂中的使用逐渐广泛；尤其在数学建模的背景下，数字工具变得越来越重要．正如Drijvers所述，数字工具的引入“开启了无法进入的新视野，并提供了探索数学情境的机会”[1]．文献中存在一个普遍的假设：在建模活动中使用的数学模型不仅受到学生数学知识和能力的影响，而且还受到可用的数字工具所提供的可能性的影响．比较而言，我国在有关利用数字工具进行数学建模的研究方面缺乏经验，而国外一些研究者已做出了一定的探索．下面主要从数字工具的内涵与价值、数字工具支持下的数学建模过程以及国外的相关实证研究三方面介绍数字工具支持下数学建模的相关研究，为我国在这一方面的未来研究提供方向．

1 数字工具的内涵与价值

关于数字工具的内涵，可从狭义和广义两方面进行阐述．狭义而言，数字工具(digital tools)指的是可以用某种特定的方式来支持学习过程的数字媒体，如计算机、平板电脑或手持设备．Borba等人认为，数字工具可以像任何其他学习工具(如几何直角尺或计算器)一样，用于回答问题、在互联网上进行调查、交流或准备教学材料[2]．广义而言，数字工具的概念已不仅仅局限于特定的设备，还包括在数学课堂中具体使用数字工具的方式．

关于数字工具的价值，目前学术界普遍赞同的观点是，数字工具可以支持学生的学习过程和教师的教学行为，即数字工具具有教育价值．例如，数字工具支持构建多种不同的表征，可同时生成相互联系的多元表征，在课堂上可以实现可视化的目的；当执行数值计算、求解方程或处理离散模型或函数模型时，可通过数字工具的图像表征功能来处理；在发现数学关系方面，数字工具在实验工作和执行调查时尤为重要．

特别说明一下，本文主要以数字工具的形式来讨论技术．尽管数字工具为解决实际问题提供了更大的机会，但对使用者也提出了更高的技术要求．

2 数字工具支持下的数学建模过程

关于数学建模的内涵，目前学术界已基本达成共识．大多数学者认为，数学建模就是从实际问题出发，经过抽象、简化，归结为数学问题，然后建立数学模型，求出结果并解释实际问题，若不符合实际，再重新修改模型，直到得到符合实际问题的模型；数学建模的过程实际上是一个可以重复多次的循环，即建模循环(Modelling Cycles)．

一些研究者结合数字工具在数学建模中的应用，从理论角度描述了数字工具支持下的数学建模循环．

Geiger认为，数字工具几乎适用于建模循环中的所有环节，并建立了技术支持下的数学建模循环模型[3](见图1)．

图1 技术促进数学建模的改编模型

Confrey和Maloney也概述了一个包括数字工具的建模模型[4](见图2)，他们同样认为数字工具整体上是适合学习的．

图2 建模模型

图3是Blum和Leiβ的七步建模循环[5]，显示了在建模过程中应用数字工具的几种可能性(见斜体)；这些数字工具的可能用途与数学建模子能力(如简化、数学化、数学操作、解释和验证等)相对应．

图3 建模中数字工具的可能能力

在建模循环的所有步骤中，Galbraith和Stillman认为，从实际模型简化为数学模型进而得到数学结果的步骤中，数字工具所发挥的作用最为明显[6]．如果我们更详细地研究建模循环中利用数字工具进行数学操作的步骤，我们就会发现，只有当数学表达式被翻译成数字工具所理解的语言时，我们才能应用数字工具；而数字工具产生的结果必须再一次被重新翻译成数学语言，才能得到一个数学结果．这样的翻译过程可由一个拓展的建模循环[5](见图4)来表示：在实际世界和数学世界的旁边，增添了一个技术世界．

早期，我国学者张思明也强调，利用数字工具(如计算机工具)并结合数学方法求解数学模型，是建模循环中一个重要的步骤[7](见图5)．

图4 拓展的建模循环(Siller和Greefrath，2010)

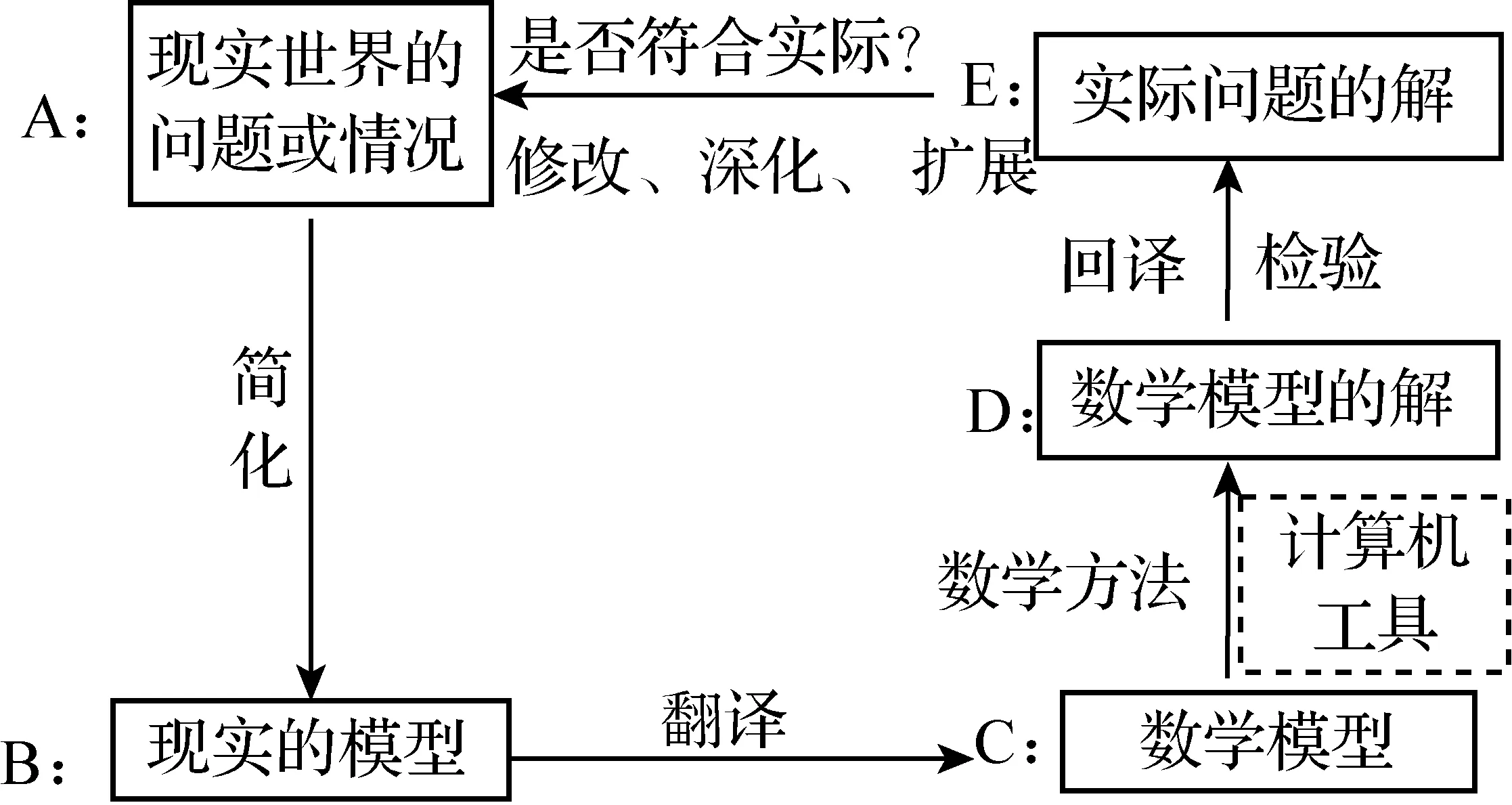
图5 数学建模的过程(张思明)

关于数字工具支持下的数学建模过程，我们可以做出这样的假设：在数学建模循环的各个环节均可能使用数字工具；在求解数学模型得到数学结果的过程中，利用数字工具的可能性最大．

3 相关实证研究

我国几乎没有与数字工具支持下的数学建模有关的实证研究，因此这里主要介绍国外的相关实证研究．

3.1 最初的元研究

对于数字工具是否促进能力发展这一问题，有几个最初的元研究值得关注．

2002年，Burrill等人为了研究中学数学中的手持绘图技术，建立了包含五个研究问题的综合研究框架(见表1)，对43项研究进行了元分析，其中有11项研究将使用手持绘图技术的学生和未使用手持绘图技术的学生进行比较，结果发现手持绘图技术的使用对学生的学习表现具有积极的影响[8]．

表1 有关手持绘图技术的综合研究框架

续表

2003年，Ellington对54项研究进行了元分析，结果表明，教学中计算器的使用促进了学生操作技能和问题解决技能的发展；使用计算器的学生对数学表现出更加积极的态度[9]．2006年，Ellington对42项研究进行了元分析，结果发现，当计算器被用于教学时，学生对于数学概念的理解得到了增强[10]．而问题解决技能和概念性理解恰恰对于成功地进行数学建模十分重要．

Burrill等人和Ellington的元研究均表明了数字工具(如手持绘图工具、计算器)对学生的学习产生了积极的影响，肯定了数字工具对于学生能力发展的作用．

3.2 更具体的研究

除了以上数字工具与能力发展方面的元研究，很多更细致的研究为数字工具支持下的数学建模研究提供了更具体的研究视角．

3.2.1定性研究

在更具体的研究视角下，一些定性研究致力于研究数学建模中数字工具的可能用途．

Doerr和Zangor针对两个初高年级班中的学生，对处理建模任务的课堂进行了观察，并分析了课堂中学生使用图形计算器的方式.研究发现，数字工具被用于计算、收集数据、可视化和检查工作[11]．因此，该研究证实了图3建模循环中数字工具的一些能力，如调查、可视化、计算和控制．

Greefrath和Siller针对四对10年级学生，观察了他们利用动态几何软件GeoGebra进行建模的过程，发现学生主要在情境模型到数学结果的步骤间利用数字工具，并将建模循环中GeoGebra的所有可能用途(见斜体)概括在图6[12]．

图6 有关建模循环中数字工具用途的定性研究结果

3.2.2定量研究

尽管以上提及的定性研究对学生的建模过程和数字工具的使用产生了更深入的了解，但定量方法为评价数字工具对学生成就的影响提供了机会．

在德国的一项定量研究中，针对177名学生，将一个利用动态几何软件学习的实验组与一个没有计算机帮助的对照组进行了比较，并测量了动态几何软件的使用对几何成就的影响，结果发现对照组的表现明显优于实验组[13]．由此可见，数字工具的使用不一定促进学生的几何成就．

2014年，Chan和Leung发表了一篇元分析文章，对2001年至2013年发表的国际定量研究进行了梳理，发现共有9项研究分析了动态几何软件对学生数学成就的影响；Chan和Leung还将DGS组(Dynamic Geometry Software，简称DGS)和对照组进行了比较，发现DGS组的数学成就更高[14]．

然而，以上提及的定量研究，均是将一般的数学成就或几何成就作为因变量，并没有将数学建模能力或数学建模表现作为测量的主要参数．

下面介绍德国的一项最新定量对照研究，该研究特别调查了学生“数学化”这一建模子能力．Gilbert Greefrath等人主要利用测试、问卷调查、观察、访谈等研究方法，在对几何建模任务进行干预的四堂课期间，将一个使用数字工具进行建模的实验组与一个使用纸和笔完成同样任务的对照组进行了比较，结果发现两组的数学成就没有显著差异，但实验组在数学化部分比纸笔组稍差；另外，他们还研究了“与程序相关的自我效能感”(program-related self-efficacy)和“对计算机的态度”这两个因素对学生“数学化”的影响，通过统计手段分析数据，结果发现，“与程序相关的自我效能感”而不是“对所使用软件的态度”，是对“数学化”能力增长的一个重要预测因素[15]．由此可见，高计算机自我效能感的学生在数学建模过程中所表现出的“数学化”能力越强．

4 反思与展望

从2003年“数学建模”正式进入高中数学课程标准，已近15年．回顾我国近15年来数学建模中数字工具的相关研究，可以发现我国现有研究中的不足；针对不足，提出建议，为我国这一方面的未来研究提供方向和思路．

4.1 我国的相关研究

相关理论研究中，除了张思明提出的数学建模过程(图4)，罗奇等人结合国内外问题求解相关理论，构建了数学建模过程的系统模式，刻画了网络环境下数学建模过程的外显求解行为和内隐认知活动[16]，也指出了计算机具有模拟实验、处理模型并优化模型等功能．然而，该模式是罗奇等人根据指导大学生建模的成功经验而构建的，其合理性是否适用于一般的数学建模过程，仍需进一步检验．

教材研究方面，吴道春聚焦于函数模型，将三个版本教材中的信息技术进行比较，发现苏教版主要用到EXCEL和计算器，北师大版主要运用的是图形计算器，人教A版主要用到计算机和图形计算器；他强调，现代计算机技术的发展赋予了建模新的要求，即把模型翻译成计算机能够识别的程序或利用数学建模软件进行模型的求解与计算[17]．

课程与教学方面，上海市高中曾做过将数学与计算机信息科学知识进行整合的教学尝试，开设了《数学建模与算法实现》课程[18]．近年，上海市某中学数学教研组开展了一系列的图形计算器支撑下的高中数学建模，利用8个实例说明了图形计算器具有以下建模功能：绘图、数列与递归、程序模拟[19]．

所有相关研究中，最多的是案例研究，即结合具体实例，介绍数字工具在数学建模中的应用．例如，施洪亮提供了一则基于图形计算器的“特拉法尔加海战”建模案例，利用图形计算器模拟了战斗进程，借助其编程、拟合等功能求解了战斗损耗系数、初始战舰数、战斗编组情况等[20]；曾志勇和周灵从建构主义学习理论、认知工具理论和多元智能理论分析了数字工具对教与学的重要性，并利用三个应用实例(函数模型、不等式模型和线性规划模型)解释了TI手持技术在初中数学建模活动中的应用[21]等．

4.2 反思

首先，我国有关利用数字工具进行数学建模的研究质量和数量有待提高．由文献可知，我国以案例研究为主，其中大部分文献都在介绍数字工具在数学建模中的应用，采用实证的研究方法探索数学建模中数字工具的用途、数字工具的使用对数学建模能力的影响等研究相当罕见．

其次，我国缺乏在利用数字工具进行数学建模这一方面长期研究且拥有一定影响力的领军人物．

再次，有关数字工具支持下数学建模的研究内容关注程度太浅，很少有研究从理论层面描述数字工具在建模循环中的应用．

4.3 建议与展望

针对以上不足，对数学建模研究者提出以下建议：

第一，加强与数字工具支持下的数学建模有关的实证研究．由于我国这一方面的相关论文文献数量太少，具有真正说服力并值得推广的研究成果并不多见．因此，未来应强化实证研究，通过调查、测试等方法拿出数据并用真实的数据来解释和证明自己的研究结论．

第二，重视数字工具在建模循环中的理论研究．至今，我国相关研究中还没有研究能全面地描述使用数字工具的数学建模过程．而数字工具在数学建模的不同阶段都可能被使用，因此很有必要从理论角度建立使用数学工具的建模循环理论框架．

第三，加强与一线教师的合作研究，形成与“数字工具支持下的数学建模”有关的专业研究团队．

汲取国外研究经验，提出以下未来研究问题：

①建模时使用或不使用数字工具，是否会影响学生的数学建模表现？建模时使用数字工具的学生获得了哪些在没有数字工具帮助时的知识或技能？

②计算机自我效能感与数学建模能力之间有关系吗？计算机自我效能感与实际建模过程之间的相互作用是什么样的？

③学生对数字工具的态度是否影响其数学建模能力的发展？

④教师或学生在数学建模过程中如何使用数字工具(如一个动态几何软件GeoGebra)？