从应用题到建模问题的回译——一种开发数学建模素材的新思路①

黄英芬 颜宝平 龙红兰

(铜仁学院大数据学院 554300)

数学建模是联接现实世界与数学世界的桥梁.把数学建模作为一门课程可以追溯到20世纪70年代，英国著名的剑桥大学率先给研究生开设了这门课程，后来人们尝试给大学本科生上，再后来给中小学生上.进入21世纪，各国数学课程标准纷纷对数学建模提出明确要求，如美国、澳大利亚、德国、瑞典、新加坡、中国等，数学建模越来越受到世界范围内教育界的关注和重视.我国的中学数学建模教学首先在北京、上海等发达地区展开实践.2003年，数学建模首次被写进《普通高中数学课程标准(实验)》，课标要求在高中阶段至少为学生安排一次完整的数学建模活动[1].这标志着数学建模成为高中生正式学习的内容.2018年初由教育部颁布的《普通高中数学课程标准(2017年版)》把数学建模作为数学六大核心素养之一，要求数学建模作为课程内容主线，并安排了具体课时[2].这意味着我国高中数学建模教学又往前迈进了一大步.至今，中国高中阶段的数学建模已经有了二十多年的积累，但相对于全国所有高中的基数来说，仍然处于起步阶段，还存在很多亟待解决的问题，教师问题就是其中之一[3].很多教师会将“应用题的练习”等价于“数学建模”[4]，不能理解数学建模的内涵.另一方面对数学建模资源的总结不够，用于全员推广的可操作性有待提高[5].现有高中数学教材中的数学建模内容贫乏，缺乏适合学生学习和教师讲解的数学建模问题，而由于种种原因，许多教师又难找到或提炼出合适的数学建模问题，致使他们在数学建模教学时有“巧妇难为无米之炊”之感[6].关于高中数学建模素材的开发，文[6]给出了几种改编高中数学建模素材的途径，但并未给出具体实例.由美国数学及其应用联合会(COMAP)、美国工业与应用数学学会(SIAM)原著，由梁贯成教授等编译的《数学建模教学与评估指南》一书中给出了如何从一个数学问题出发改编成一个建模问题的例子[7]，但受经验的限制，难度较大.本文将给出一种简单实用的开发高中数学建模素材的新思路，期望对广大一线教师有借鉴意义.

1 数学建模的内涵

通俗地讲，数学建模就是建立数学模型解决实际问题的过程.《普通高中数学课程标准(2017版)》把“数学建模”定义为是对现实问题进行数学抽象，用数学语言表达问题、用数学方法构建模型解决问题的过程[2].如果问题没有得到很好地解决，还需要重复进行建模过程.

2007年，Blum和Leiβ提出建模七阶段循环过程[8]，即把整个建模过程分为七个环节，六个状态(如图1)：

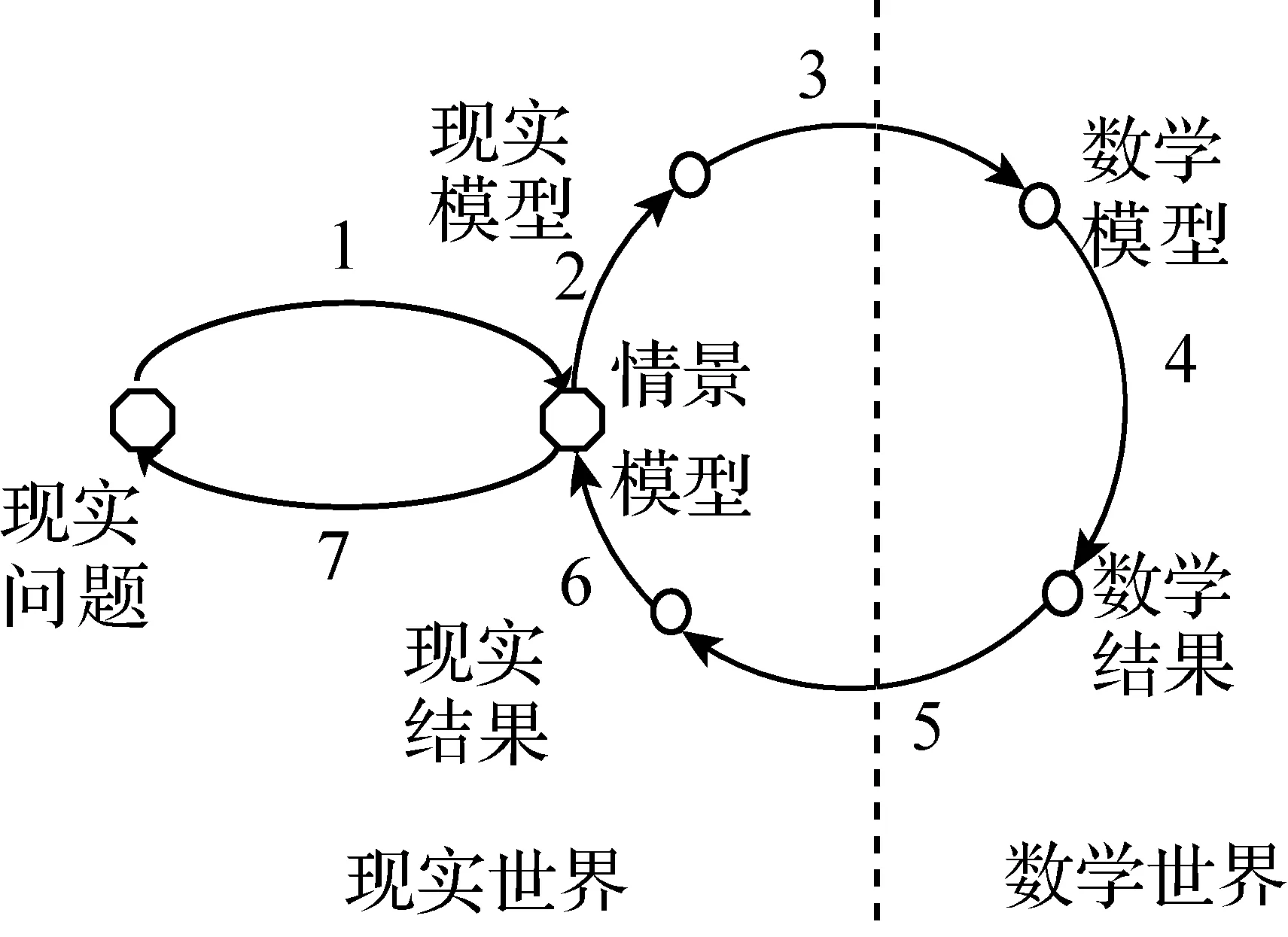
图1 七阶段建模循环模型

(1)理解“现实问题”构造“情景模型”；

(2)简化“情景模型”构造“现实模型”；

(3)数学化，即用数学的语言描述“现实模型”从而构造“数学模型”；

(4)运用数学方法得到数学结果；

(5)根据现实问题解释数学结果，获得现实结果；

(6)结合原来的情景验证结果，如果答案差强人意，则重新进行建模过程；

(7)介绍问题解决方案，并与他人交流.

数学建模是一个过程，而最重要也是学生感觉最困难的是“现实问题→……→数学模型”这一子过程.为了更好地提高学生的数学建模能力，寻找一个好的数学建模问题是关键.

2 建模问题与应用题

90年代初期，我国高考题中开始出现应用题，并延续至今.长期以来，我国已有丰富的应用题资源.谈起应用题，一线教师可谓如数家珍.不难发现应用题的特点：(1)抽象性.有实际背景，但已经对现实进行过度简化、提炼和抽象.(2)确定性.问题表述清楚，条件不多也不少，所需数据明确给出，答案唯一.(3)封闭性.学生完成这个问题不需要考虑实际情况，只需要理解题目中的数量关系或空间形式，恰当地使用数学知识便可以解决问题，不需要反复修正.

与应用题相比，建模问题没有明显的数据和关系可用，给出的条件也不一定有用，学生需要自己做出假设，并筛选数据和有用的条件，得出的结论往往不唯一.建模问题具有现实意义，学生得到数学结果后，必须考虑实际，若结果不符合实际，则需要返回到最初并重新做出假设.因此，建模问题具有现实性、模糊性、开放性.

从建模七循环过程，可以看出应用题应该介于“现实问题”与“数学模型”之间，即“现实问题→……→应用题→……→数学模型”.应用题是对现实问题的抽象和简化，只包含问题的基本要素，从而更易于数学处理.现实问题就是指来自现实世界的建模问题.我们要把一个应用题改编成一个建模问题，就是对上述过程的回译，即需要隐藏某些数据，降低应用题的抽象层级，重拾被应用题抛弃的细节，把提炼的条件重新放回现实中，从而改变应用题的三个特性，实现从应用题到建模问题的华丽转身.

3 实例

应用题1城市居民购置一辆小轿车需一次性投入12万元.使用期间每年还需支付保险、维修、汽油、养路费等维持费：第一年需8000元，以后每年递增12%(假设维持费在每年年初支付).车辆使用10年后报废.问：在这10年内，相当于每年投入多少资金(设银行年利率为3%)？(上海市1999年决赛)[9]

经过分析，不难发现“数据明确且不多不少，问题清楚”是导致其封闭的关键因素.想要破坏应用题的这一特性，首先需要观察并调整数据.

第一步：调整数据.题目不仅给出需要考虑的因素，还做出假设如维持费的逐年递增率，车辆使用的年限.题目还提示要考虑银行存款年利率.学生做题时，不需要考虑实际情况，只需要根据题目给出的条件找到数据之间的关系即可解决问题.为了让题目具有开放性，现在我们隐藏数据“8000、12%、3%”，让学生去调查并估算这些数据.我们暂时把它称为“开放应用题”.

开放应用题1城市居民购置一辆小轿车需一次性投入12万元.使用期间每年还需支付保险、维修、汽油、养路费等维持费.假设车辆使用10年后报废.问：在这10年内，相当于每年投入多少资金？

学生为了解决问题会去调查一辆价值12万的小轿车一年的维持费需要多少，最初可能并没有考虑到维持费可能会逐年递增，但调查的过程中，车主可能会无意中说到维修费用等会逐年增加，但是“12%”这样的数据却是需要自己去估算的.缺少了“银行利率3%”的提示，大多数同学可能会忽略这一点.学生在讨论中，会逐渐完善这些信息.同时，他们也明白了现实生活中的问题不像书上的应用题那么清晰、明确.这个问题虽然开了一扇窗，让学生亲身经历了搜集、估算数据的过程，但是还缺乏更加实际的意义.现在我们给它寻找一个更加贴近实际的情景.

第二步：现实化.想一想对于收入一般的家庭，准备买车的时候在思考什么？他可能很纠结买车以后方便了出行，但是增加了开支.

建模问题1假如你的父母是该市的普通上班族，现在决定买一辆家用汽车，请你综合考虑汽车的价格，以及使用期间所要支付的保险、维修、汽油、养路费等，为你的父母测算适合买一个什么价位的汽车.

经过改编，问题变得开放了，学生想要完成这个问题，必须去了解父母的收入，家庭开支，以及养一辆汽车所需的费用等.学生在做调查的同时，也能感受到买车不是越贵越好，有利于消除攀比心理，这使问题变得更加有意义.

第三步，延伸.为了把问题做得更深入，除了从经济上，还应综合考虑汽车的配置、舒适、美观等因素，做出综合决策方案.

第四步，发散.除了买车，还可以考虑买房.假设你的父母购买住房时需要贷款30万元，他们希望尽可能少付一些利息即尽量缩短贷款年限，又希望每个月还完房贷后对家庭生活质量不要产生太大影响.现在请你为父母设计一个合理的贷款方案.

还可以考虑贷款时，采用“等额本金”还是“等额本息”的方式来还款.过了几年以后，你父母的月收入增加了，想要提前还贷，你还可以为他们计算已还多少本金和利息，还剩多少本金和利息，为他们的决策提供参考……

应用题2设A、B两点在河的两岸，要测量两点之间的距离.测量者在A的同侧河岸边选定一点C，现测得AC=55 m，∠BAC=101°，∠ACB=55°(如图2).求A、B两点的距离(精确到1 m).

图2

第一步：调整数据.由于题目中已经测得相关数据，学生只要联想到正弦定理，问题便迎刃而解.为了达到让学生自己体验的目的，我们应该隐藏“AC=55 m,∠BAC=101°,∠ACB=55°”这些数据，留给学生自己去测量.经过这样的改编，题目具有了一定的开放性，我们暂时把它称为开放应用题.

开放应用题2为了测得河岸两点A、B间的距离，在A的同一测选择一点C(如图3)，并测量AC的长度，∠BAC，∠ACB的度数，求AB的长(精确到0.1 m).

图3

经过改编，题目具有一定的开放性.学生不同的选择会导致AC过长或过短，经过计算会发现过长或过短可能导致误差过大，于是会重新调整.还有的学生为了减少误差可能会选择多测两次，取平均值.另外就是角度的测量，合适的测量工具可能显得很重要.总之，在这样的过程中，学生能够体会到数学在现实中的应用.但是这个问题的开放程度还不够，因为题目给出了测量方案，包含明确的数学提示，这样会限制学生的发散思维.

第二步：现实化.为了构建更加贴近实际，更加开放的建模问题，我们需要还原真实情景.第一，我们可以把“测量地面上两个不可到达的地点的距离”作为问题，给建模者留出自由发挥的空间.第二，给这个问题寻找一个理由，并还原到真实场景.

于是，我们可以得到：

建模问题2某市有一不规则湖泊(如图3)，居住在D区的人想要到过E区需要绕很远的路.鉴于此，市政府决定在D、E两区(即A、B两点)之间建立一座桥.请你运用所学知识设计一个方案来测量一下A、B两点之间的距离，以方便估算建桥所需的材料.

经过改编，学生感觉自己做这道题目是有意义的，并且可以根据自己所掌握的知识选择不同的测量方案.如果学生对正弦定理的内容比较熟悉，就可以选择应用题2中的方案，利用正弦定理来解决问题.也有学生对初中学过的全等三角形的知识印象深刻，于是想到利用全等三角形的知识把测量A、B的距离转化到测量岸边上某线段的长度.即在AB的垂直线上取两点C、D，并使得CD与AC的长度相等，做DE⊥AD，并使得E与B、C在同一直线上(如图4)，根据三角形全等的知识，可知测得DE的长度就能知道AB的长度.类似地，当CD与AC的长度不相等时，可以利用相似三角形的知识求得AB.最后，小组间进行交流，可以拓宽知识，感受运用数学知识解决实际问题的可行性与灵活性.同时，也说明经过回译得到的题目是一道真正的建模问题，它的开放性决定了可适用于不同层次的中学生做.

图4

第三步：延伸.在建模题2中，我们事先选定了A、B两点.而在实际问题中，我们关心的是怎样选择A、B两点，才能使得AB最短.

第四步：发散.现实生活中，关于测量的问题不止这一个.有的时候，我们还需要测量不能到达的河对岸两点之间的距离.

我们不仅可以测量平面上两点的距离，也可以测量空间中某个物体的高度，比如旗杆，市内某个很高的建筑物……

通过上面两个例子，我们可以发现把一道应用题回译成一道或若干道建模题，需要经历以下四个步骤：

(1)调整数据：隐藏那些适于学生调查或测量的数据，给学生留出亲身体验的机会.

(2)现实化：重新组合题目的要素，并还原真实场景，使问题更加有意义.

(3)延伸：考虑解决这个问题更多、更实际的因素，以使问题得到更好的解决.

(4)发散：联系类似的情景，以便找到更多的建模问题.正如波利亚指出：“好问题同某种蘑菇有些相像，它们都成堆地生长……当你找到第一个蘑菇或做出第一个发现后，再四处看看，就能发现一堆蘑菇.”

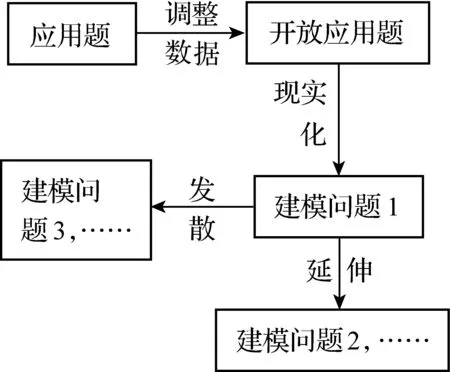
图5 从应用题到建模问题的回译过程

新课标对数学建模的要求，表明了下一阶段将在高中阶段全面推进数学建模的教学.数学建模是将数学应用到现实生活的过程，非常值得教师在数学课堂引入相应教学以加强学生学习数学的动机和兴趣.然而，到目前为止，还有很多高中学校并未实际开展数学建模活动，还有相当数量的数学教师并不知道数学建模的涵义.本文所给出的开发数学建模素材的方法正是为这些教师准备的，教师可以通过这种方式感受什么是简单的建模问题，也可以用“延伸”、“发散”的思维方式引导学生发现并提出新的问题.