在层次性探索中发展数学思维——以研究“轴对称视角下线段和的最小值问题”为例

杨丽娟

(昆山市葛江中学 215300)

美籍匈牙利数学家乔治·波利亚，在《怎样解题》中启发学生：解决数学问题要善于联想——你以前见过它吗？你是否知道与此有关的问题？你是否知道一个可能用得上的定理？这里有一个与你现在的问题有联系且早已解决的问题，你能不能利用它？你能利用它的结果吗？你能利用它的方法吗？…[1]以上启发，其实质是：“看到问题，唤醒知识；解决问题，类比应用”．用数学思考问题和解决问题的思维活动形式,就是数学思维,笔者以专题“轴对称视角下线段和的最小值问题”的课堂教学为例，说明在数学课堂教学中，如何通过真实的问题情境，让学生明确学习任务，驱动学生围绕主题开展数学活动，进行层次性的探索，最终解决问题，发展数学思维．

1 利用生活情境，唤醒知识生长点，点亮数学思维的火花

在研究轴对称视角下线段和的最小值问题时，通过创设简单真实、贴近学生实际生活的问题情境，唤醒最值的有关知识．

情境1如图1，从甲地到乙地有3条路，走哪条路相对近一些？并说明理由．

图1

情境2如图2，污水处理厂要从A处把处理过的水引入排水沟PQ，应如何铺设排水管道，才能使用料最省？试画出铺设管道的路线？并说明理由．

图2

设计意图通过设计与教学内容相关联的生活情境，唤醒相关的数学基本事实，点亮学生思维的火花，为后续探索提供理论依据．利用情境1，获得基本事实：两点之间，线段最短，强调两点之间的最小值问题；利用情境2，过点A作AB⊥PQ，垂足为点B，线段AB即为铺设的最短管道，从而获得基本事实：垂线段最短，强调点到直线的最小值问题．

在解决情境问题时，抓住知识的生长点，引发数学思维，培养学生科学的态度和理性精神．

2 明确学习任务，进行层次性探索，搭建数学思维的桥梁

“任务驱动”是建立在建构主义教学理论基础上的，有利于培养学生自主学习与协作学习能力的教学方法．初中生的数学学习活动必须与任务或问题相结合，让学生带着具体的任务去自主学习与协作学习，借助探索问题来驱动和维持学生学习的兴趣和动机．

在研究轴对称视角下线段和的最小值问题时，利用“两点之间，线段最短”解决“牧童饮牛”这个经典的实际问题，构建相应的数学模型，并在此基础上进行类比探究，搭建数学思维的桥梁，层层深入，以此培养学生的数学思维能力．

2.1 数学模型1：已知直线异侧两定点，找一动点

如图3-1，在A村庄和B村庄之间有一条小河(看作直线l) ．夕阳西下，牧童想从A村庄到河边将牛饮足水，然后回到在B村庄的家．请你帮牧童找到饮水点P，设计一个最短路线，并给出你的理由．

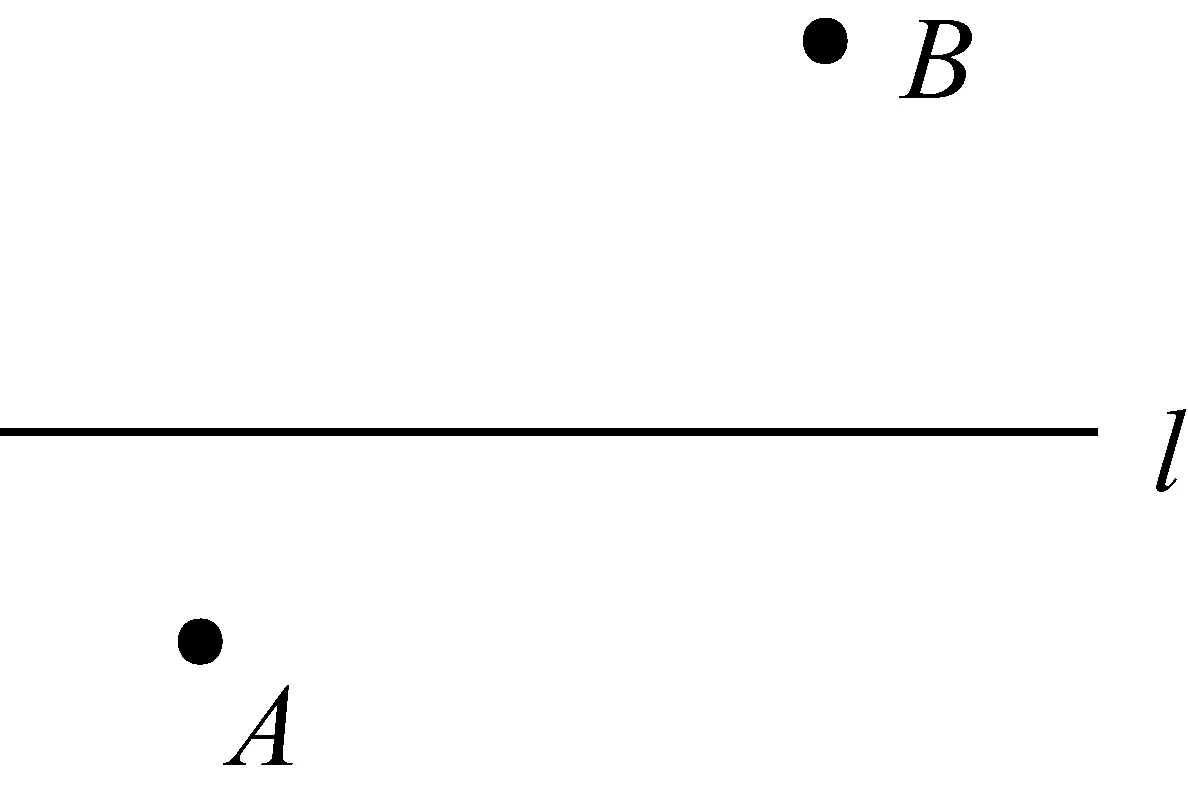
图3-1

图3-2

分析这里我们将A村庄与B村庄看成两个固定的点，位于直线l的两侧，要在直线l上找一个点到这两个点距离和最小，利用“两点之间，线段最短”，只需连接这两个点，与直线l的交点即为所求点P(如图3-2)．

2.2 类比探究：选址造桥

上述问题中，如图4-1，如果A村庄和B村庄之间隔着的小河宽a米(a是一个已知数)，现在需要在河面上架设一座桥(桥面与河岸垂直)，牧童从A村庄出发走到桥边让牛饮足水，然后过桥回到在B村庄的家．那么这座桥应架在何处，才能使牧童所走的总路程最短？

图4-1

图4-2

分析先让学生试着通过直观想象画出牧童的行程示意图，如图4-2，那么如何确保牧童所走的总路程最短？即AC+CD+BD最小？这里CD是不变量，只要AC+BD最小即可，类比数学模型1，想办法将分散的线段AC、BD聚拢在一起．假设河宽忽略不计，即将河的一岸平移到对岸，利用动画演示平移过程，在平移过程中点A平移到点A1，构建出数学模型1的基本图形．就点A1到点B路程最短怎么办？连接A1B交对岸于点D，过点D作两岸间的垂线段CD，CD即所架设的桥，然后动画演示恢复河宽，发现A1D平移到AC上，即A1D=AC，所以AC+CD+BD=A1D+CD+BD=A1B+CD最小．

设计意图本题实质还是强化已知直线异侧两定点，在直线上找一动点，求线段和的最小值．在解题过程中感知所用方法——平移不变量，聚拢分散线．

2.3 数学模型2：已知直线同侧两定点，找一动点．

如图5-1，一条小河(直线l)的同侧有A和B两个村庄.夕阳西下，牧童想从A村庄到河边将牛饮足水，然后回到在B村庄的家．请你帮牧童找到饮水点P，设计一个最短路线，并给出你的理由．

图5-1

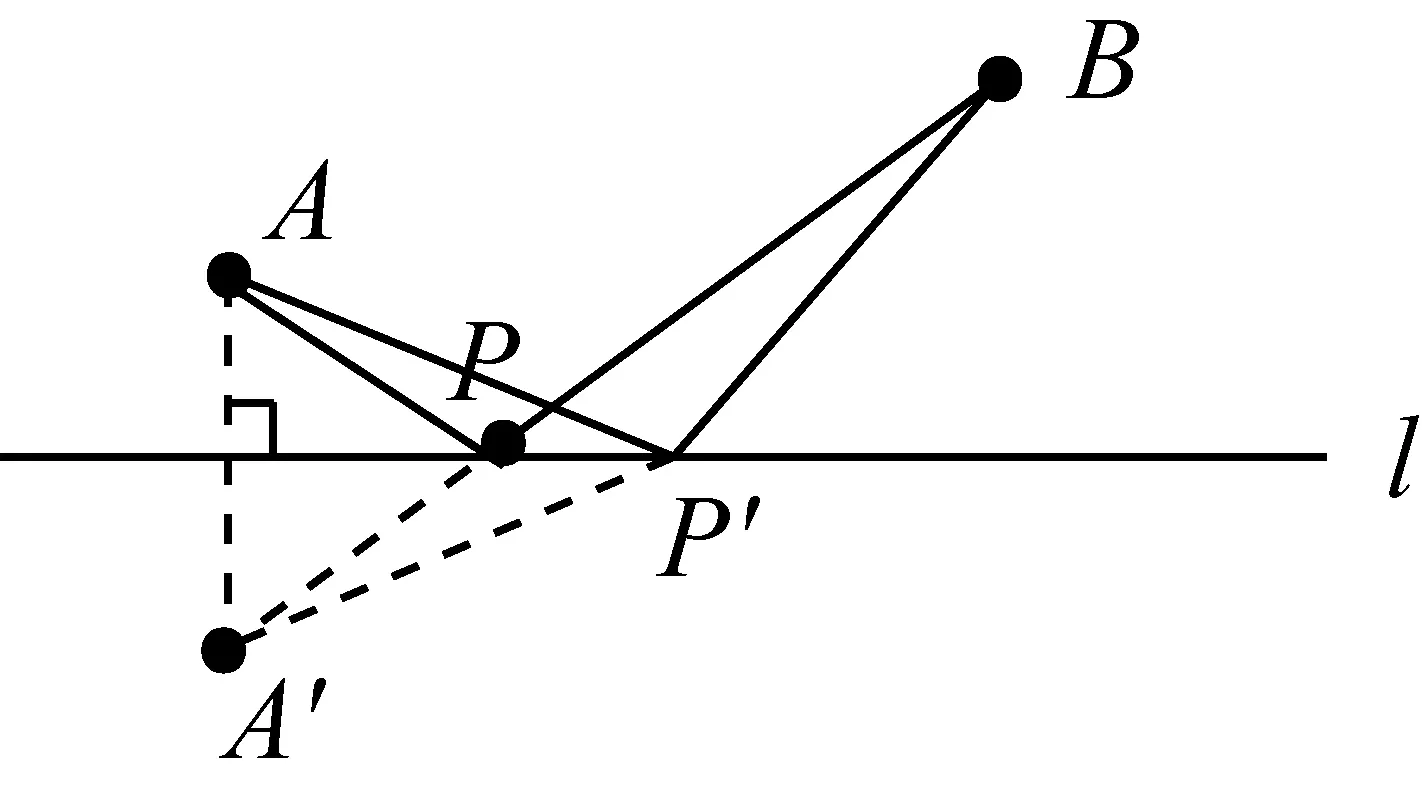
图5-2

分析这里我们将A村庄与B村庄看成两个固定的点，位于直线l的同侧，要在直线l上找一个点到这两个点距离和最小．如图5-2，作点A关于直线l的对称点A′，即利用轴对称将点A翻折到直线l的异侧，得到点A′，变成数学模型1，连接A′B交直线l于点P，根据轴对称性质可知PA=PA′，则PA+PB=PA′+PB=A′B．另取一点P′，连接P′A、P′B，根据轴对称性质可知P′A=P′A′，则P′A+P′B=P′A′+P′B，很明显PA′+PB在一直线上最短．这里已知直线同侧两定点，在直线上找一动点，求线段和的最小值．在解题过程中感知所用方法——作轴对称，拉直线段；理由是：两点之间，线段最短．

设计意图借助牧童饮牛的问题情境，明确学习任务，研究线段和的最小值问题，通过变式与类比，说明解决实际问题应先建立数学模型．

3 点拨疑难困惑，经历延伸拓展，开拓数学思维的宽度．

数学教学不仅要向学生传授知识与技能，更要传授数学思想和方法，重视培养学生的思维能力、创新意识和情感价值观，要体现思维的主动性和创造性．教学中面对知识的疑难点，学生会茫然不知所措，或四处出击一无所获，教师应遵循学生思维发展的规律，通过点拨思维方向与思考方法，帮助学生拓宽思维路径．

继续以牧童饮牛为背景，开展系列数学活动，适时进行知识延伸拓展，给学生留下思维发展的空间．

数学模型3：已知平面内一定点，找两动点

例1(1)如图6-1，已知∠AOB内部点P处拴着一匹牛，牧童先牵牛去草地(OB上)吃草，再去河边(OA上)饮水，然后回到点P，请你帮牧童设计最短路线(要求画出图形) ．

图6-1

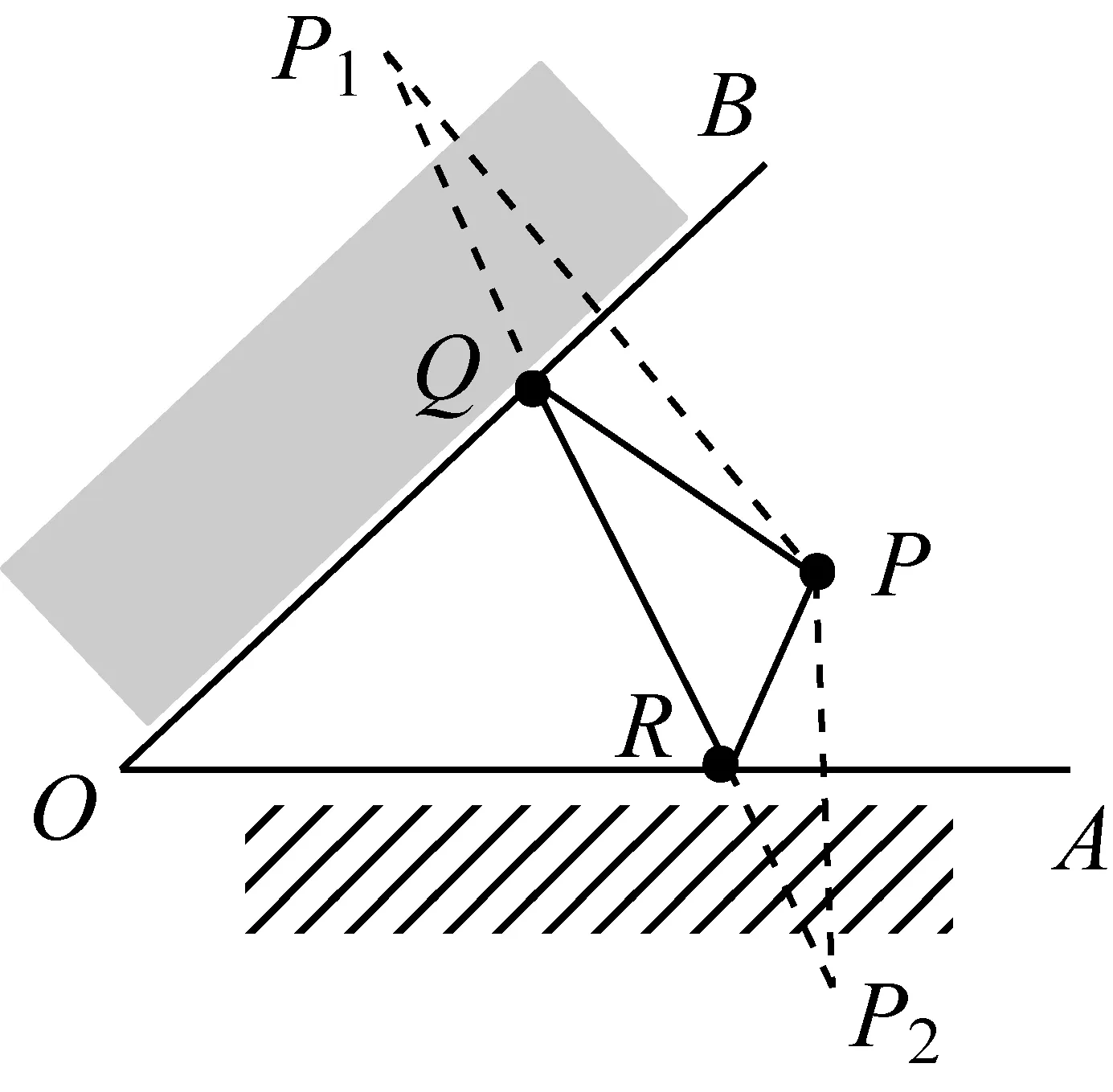
图6-3

分析先让学生试着画出牧童的行程示意图，如图6-2，使PQ+QR+PR最短，这里定点是点P，求两动点Q、R，变为一定点两动点的问题．怎样使三条线段的和最小？结合之前总结的方法：作轴对称, 拉直线段；两点之间，线段最短．思考作哪个点关于哪条直线的对称点，通过翻折找到与之相等的线段．

如图6-3，作点P关于OB的对称点，使点P翻折到直线OB的异侧点P1；作点P关于OA的对称点，使点P翻折到直线OA的异侧点P2．这样，P1、P2两点在∠AOB两边的异侧，连接P1P2，交OB于点Q，交OA于点R，则PQ+QR+PR=P1Q+QR+P2R=P1P2最短．Q，R即为所求.

(2)若∠AOB=45°，PO=10，求路线的最小值．

例2如图7-1，在锐角△ABC中，AC>AB，∠BAC的平分线交BC于点D，M、N分别是AD和AB上的动点，求BM+MN的最小值．

图7-1

图7-2

图7-3

图7-4

分析先让学生试着画出符合题意的草图(如图7-2)，这里定点是点B，求两动点M、N，还是一定点两动点的问题．因为AD是∠BAC的平分线，所以可将AD看作对称轴，作关于直线AD轴对称的点，通过翻折找到对应相等的线段，因为条件限制只能得到定点B的对称点，要作出所求的两个动点，通过“拉直线段，求线段和的最小值”还不行，还需利用垂线段最短．

方法1：如图7-3，作点B关于直线AD的对称点B′，根据角平分线的轴对称性，点B′在直线AC上，过点B′作直线AB的垂线段B′N，垂足为点N，交AD于点M，则BM+MN=B′M+MN=B′N最短．

方法2：如图7-4，对于预设的点N，可作关于直线AD的对称点N′，根据角平分线的轴对称性，点N′在直线AC上，只要确保点N′、M、B在一直线上，且BN′⊥AC即可，则BM+MN=BM+MN′=BN′最短．

说明通过对两种方法进行比较，发现方法1比较好，应尽量作定点B的对称点，因为动点N

存在不确定性．该问题利用轴对称性作对称点后，虽然可以将线段拉直，但因为只有一个定点，作出对称点后，还要注意利用“垂线段最短”等基本事实．

设计意图例1、例2涉及的元素较多，学生独立解决有困难．教学中应引导学生根据条件画出草图，利用数学知识的生长点“两点之间线段最短”、“垂线段最短”进行具体化的数学构思，在思考问题和解决问题的过程中，学会构建数学模型，透过现象看本质，培养科学独特的数学思维方式．

4 通过归纳感悟，实现问题解决，提升数学思维的高度

数学专题课是课堂教学的重要补充，本节课通过对线段和的最小值进行一系列层次性的探索，分清问题所涉及的定点与动点，以及它们之间的位置关系，让学生经历直观想象、动手操作、逻辑推理，找到解决问题所需的铺垫方法，构建数学模型，帮助学生整体把握转化思想，提升数学思维的高度，最终获得解决问题的策略：对于直线同侧的点，无论是已知两定点求一动点，还是已知一定点求两动点，都应通过轴对称转化成直线异侧的点，从而求得线段和的最小值．在解题过程中，可以用一些通俗易懂的语言总结归纳解题技巧，如：“平移不变量，聚拢分散线”、“作轴对称，拉直线段”等，最终以流程图简单扼要说明解决“轴对称视角下线段和的最小值问题”的途径(如图8)．

图8

在轴对称视角下，探索线段和的最小值问题，通过专题教学让学生获得数学的眼光，培养数学的思维，形成数学的语言，实现在层次性探索中发展学生的数学思维．