高速脂润滑圆锥滚子轴承保持架动态稳定性分析
吴正海,徐颖强,邓四二,曹栋波
(1.西北工业大学 机电学院,西安 710072;2.河南科技大学 机电工程学院,河南 洛阳 471003)
圆锥滚子轴承作为分离型轴承,因其承载能力大、可承受径向和轴向及联合负荷、可调节性好和寿命长等优点,被广泛应用于精密、高速和重型机械设备中。其中,采用脂润滑的滚动轴承占比达90%以上[1],脂润滑可有效避免润滑和密封装置的复杂性,提高轴承承载、减震和降噪性能。随着高速转子系统的发展,对轴承的精度、寿命和可靠性要求越来越高,因此轴承的动态性能也显得尤为重要,保持架动态不稳定性往往会导致保持架早期破坏,影响轴承功能的维持。
有关滚动轴承的动力学问题,国内外学者已进行了广泛研究。Walters[2]最早建立4自由度球轴承动力学模型和6自由度轴承保持架模型,开创性地分析保持架与滚动体的动态特性。Gupta[3]建立了非润滑状态下圆锥滚子轴承动力学模型,并开发了轴承动力学分析软件ADORE,对滚动体歪斜、打滑等问题进行了研究。Creju等[4]提出了双列圆锥滚子轴承的综合动力学模型,研究了非Newton流变模型下的拖动等性能,但忽略了保持架的平移运动。胡广存等[5]基于滚动轴承动力学理论,建立了油润滑双列圆锥滚子轴承动力学模型,研究了滚动体打滑、歪斜和轴承寿命等动态性能。郝烨江等[6]分析了轴箱轴承内部的载荷分布规律和影响因素,并利用ABAQUS-explicit对简化的轴承动力学模型进行了求解。盖利森等[7]建立某型高速列车轴箱双列圆锥滚子轴承三维动力学模型,并仿真分析了滚动体接触应力变化规律和保持架的运动稳定性。与其它滚动轴承相比,目前对圆锥滚子轴承及其保持架动力学问题的研究相对较少。
鉴于对脂润滑圆锥滚子轴承保持架动力学的研究现状,本文在考虑圆锥滚子轴承保持架与圆锥滚动体和引导套圈动态接触关系的基础上,基于脂润滑弹流润滑理论和挤压膜润滑理论对圆锥滚子轴承保持架全动力学模型进行了分析,并探讨了载荷、速度、预紧量和保持架材料等对保持架动态稳定性的影响。
1 圆锥滚子轴承保持架动力学模型
由于圆锥滚子轴承各组件与保持架之间相互作用的动态不稳定性,使保持架运动处于涡动状态。为准确描述轴承各组件的相对位置和运动学关系,如图1所示,建立圆锥滚子轴承惯性坐标系o-xyz,坐标原点为轴承质心,o-x轴与轴承转轴重合。保持架定体坐标系oc-xcyczc,原点为保持架质心,且随保持架一起转动。滚动体定体坐标系为or-xryrzr,原点为滚动体质心,or-xr与滚动体自转轴线重合。
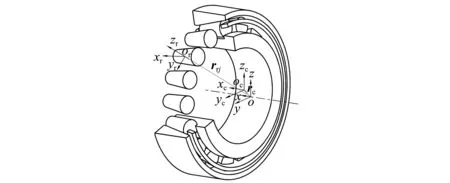
图1 轴承坐标系Fig.1 Bearing coordinate system
圆锥滚子轴承保持架结构与其它轴承保持架相比存在一定的差异,在轴承运转过程中,保持架兜孔和定心表面分别与滚动体和引导套圈直接作用,作用力解析关系较为复杂。如图2所示,保持架在涡动时,兜孔与滚动体将发生接触碰撞,在考虑脂润滑效应时,接触状态也会产生变化。同时,保持架定心表面受到引导套圈的作用,以及油气混合物对表面的黏滞阻力矩。此外保持架也会受到偏心离心力的作用。
1.1 保持架与圆锥滚动体的作用力
圆锥滚动体在保持架兜孔内既绕着自身轴线自转,同时又绕轴承转轴公转,并推动保持架一起运转。在保持架和滚动体运转过程中,力作用的主从关系将随相对速度和位移的变化而改变。如图1所示,用卡登角(Cardan Angles)描述保持架和滚动体的刚体转动,在保持架兜孔坐标系中,第j个滚动体中心相对于兜孔坐标系原点的位置矢量为

图2 保持架受力示意图Fig.2 Sketch of force on cage
rcrj=Bcj(A(rrj-rc)-r0j)-rej
(1)
式中:rc,rrj分别为保持架和滚动体的质心在惯性坐标系中的位置矢量;r0j为保持架兜孔中心在保持架坐标系中的位置矢量(常量);rej为保持架坐标系中滚动体质心相对于其中心的位置矢量(常量);A为惯性坐标系到保持架坐标系的转换矩阵;Bcj为保持架坐标系到兜孔坐标系的方向矩阵(常量)。
如图3所示,第j个圆锥滚动体与保持架梯形兜孔横梁的间隙δj为
δj=Δδ-rcryj
(2)
式中:Δδ为滚动体与兜孔横梁之间的初始间隙,Δδ=(Lc-Dw)/2;Lc为兜孔平均宽度;Dw为滚动体平均直径;rcryj为滚动体中心相对于兜孔中心的周向位移。
假设Δh0为接触状态转换的油膜厚度临界值。当δj≥Δh0时,滚子与梯形兜孔间仅存在流体动压作用,而无Hertz接触作用[8-9]。横梁与滚动体之间的等效油膜刚度和油膜阻尼分别为[10]
(3)
(4)
(5)
(6)
式中:α为黏压系数;uj为卷吸速度;R为当量曲率半径;E为当量弹性模量;Le为滚动体有效长度。润滑脂Herschel-Buikley本构方程τ=±(τy+φγn),其中:τy为屈服应力;φ为塑性黏度;γ为剪应变率;λn=(2n+1)/(n+1),n为塑性指数;η0为基础油动力黏度;h0j为最小油膜厚度;ξ1,ξ2为与塑性指数相关的常数。
则滚动体与横梁的接触力和接触摩擦力,即油膜动压力Qcj和油膜剪切摩擦力Fcj为
(7)
(8)
式中:ζ为与润滑脂流变参数相关的变量[11-12]。
当δj<Δh0时,滚子与梯形兜孔间存在流体动压作用,也存在Hertz接触作用。润滑脂最小油膜厚度为
(9)
圆锥滚动体与兜孔横梁之间的Hertz接触变形为
δhj=Δh0-δj
(10)
存在Hertz接触时,横梁与滚动体的接触力和摩擦力为
(11)
Fcj=μsQcj+Fcehlj
(12)
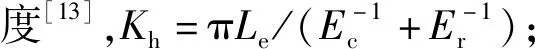
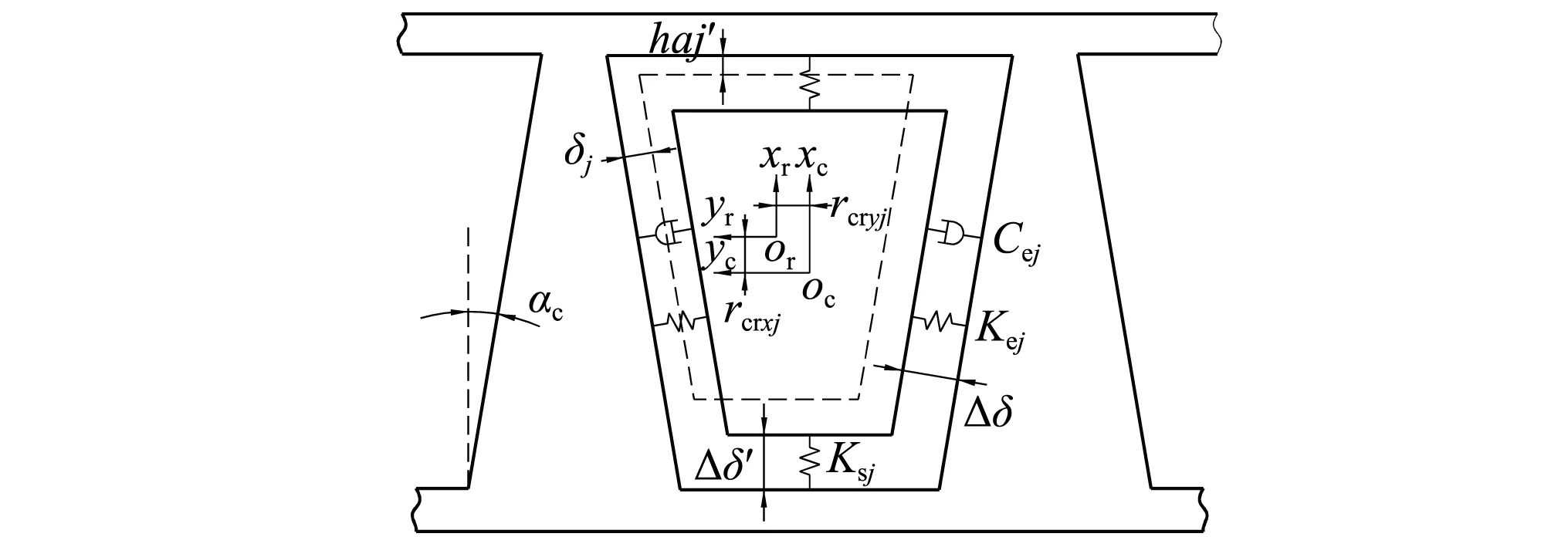
图3 等效刚度和阻尼Fig.3 Equivalent stiffness and equivalent damping
考虑保持架为6自由度运动,在发生轴向刚体位移或径向偏转时,兜孔侧梁将会与滚动体端面发生接触,由于侧梁与滚动体平端面的结构特点,在接触处无法形成弹流润滑状态,但会形成挤压膜润滑。假设兜孔侧梁与滚动体端面的初始间隙为Δδ′;raj为第j个圆锥滚动体中心相对于兜孔中心的轴向位移,raj=rcrxj。若draj/dt≥0,侧梁与滚动体小端端面接触;若draj/dt<0,则侧梁与大端端面接触。挤压膜等效刚度为[16]
(13)
式中:haj为保持架兜孔侧梁至滚动体端面的距离;haj=Δδ′-raj;Δδ′=(Lch-Lh)/2;Lch为梯形兜孔高度;Lh为滚动体高度;Db和Ds分别为滚动体大段和小端直径;b为保持架厚度。
侧梁与滚动体端面的油膜挤压力和拖动力为
(14)
Fsj=μsQsj
(15)
式中:μs为侧梁与端面接触的摩擦因数。
1.2 保持架与引导套圈的作用力
考虑每个滚动体对保持架的作用力矢量均不相同,致使保持架产生偏心,高速运转又导致保持架动不平衡。根据保持架定心面和套圈引导面的几何特点,视润滑接触为有限短轴颈轴承润滑。在径向平面内,保持架与引导套圈接触作用关系如图4所示。
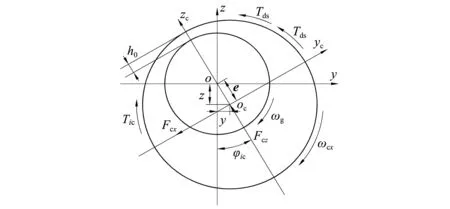
图4 保持架与引导套圈接触作用关系(内圈引导)Fig.4 Contacts between cage and guide ring
与兜孔横梁与圆锥滚动体接触分析类似,保持架定心表面与套圈引导面的间隙Δh′为
Δh′=Δe-‖e‖
(16)
式中:Δe为引导面初始间隙,Δe=(Ry-Rd)/2;Rd为定心面半径;Ry为引导面半径;e为径向平面内的位移矢量。

(17)
(18)
式中:k1和k2确定方法与兜孔横梁和滚动体接触刚度分析时一样;u为卷吸速度;Ric为当量曲率半径。
定心表面和引导面的接触力和切向摩擦力为
(19)
(20)
式中:ωg为引导套圈转速;ωcx为保持架转速。

(21)
存在Hertz接触时,保持架定心表面与套圈引导面之间的接触力和摩擦力矩分别为
(22)
Tic=μsFic+Ticehl
(23)
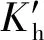
1.3 油气混合物对保持架的黏滞阻力矩
保持架除受滚动体和引导套圈作用外,其表面还受到轴承内腔油气混合物的黏滞阻力。如图4所示,保持架端面和锥形表面受到的黏滞阻力矩Tde,Tds分别为[17]
(24)
Tds=τsAcrc
(25)
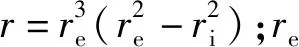
(26)
(27)
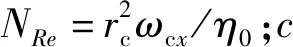
1.4 滚动体受力分析
圆锥滚动体受载荷分析属于静不定问题,需借助大量辅助方程解决,采用“切片法”对第j个滚动体进行受力分析,如图5所示。
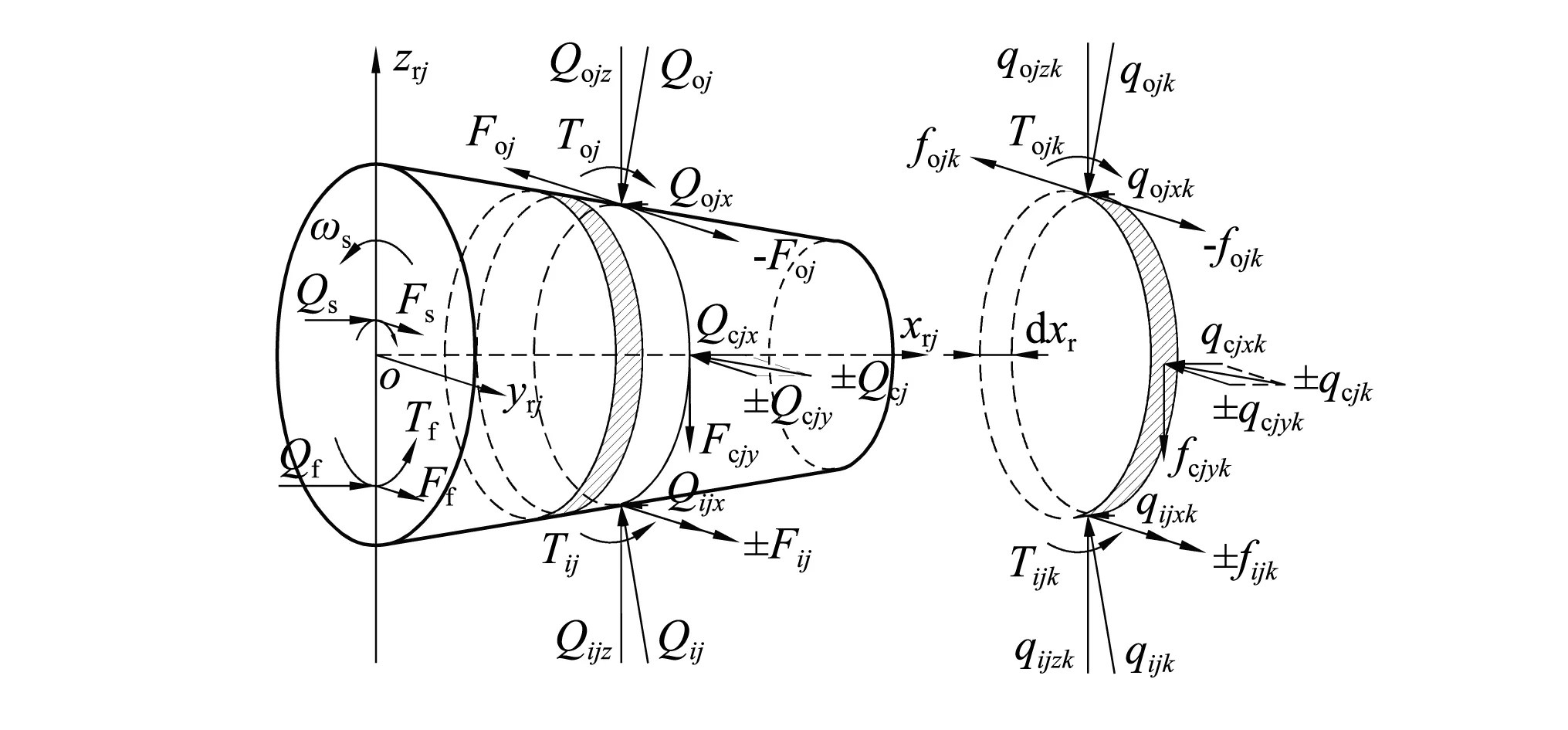
图5 圆锥滚动体受力分析Fig.5 Force analysis for a tapered roller
假设使轴承充分润滑,考虑脂润滑弹流油膜拖动力Foj(ij)。第j个滚动体的接触载荷,可由每一片与滚道接触载荷沿滚动体素线积分得到,即
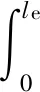
(28)
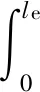
(29)
Ffj=μsQfj=μssinβ(Qoj+Qij)
(30)
式中:Qij,Qoj分别为圆锥滚动体与内外滚道的接触力;Qfj和Ffj分别为滚动体与内圈挡边的接触力和摩擦力;β为滚动体半锥角。
1.5 保持架动力学模型
在惯性坐标系o-xyz中,保持架平动微分方程为
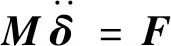
(31)
式中:M为质量惯量矩阵;δ为保持架在惯性坐标系的平动位移列向量;F为保持架所受外力列向量
(32)
式中:m=1为保持架兜孔横梁与滚动体接触作用力;m=2为兜孔侧梁与滚动体接触作用力;Fce为保持架偏心离心力。
在定体坐标系oc-xcyczc中,保持架旋转运动用欧拉动力学方程描述
ψ=AN
(33)
(34)
式中:Ix,Iy,Iz为保持架主惯性矩;ω为保持架在惯性坐标系中的角速度;N为保持架承受的外转矩,在惯性坐标系中将各零件的接触转矩叠加得到。
(35)
保持架在定体坐标系中的角速度ωc与ω的关系如下,其中B为转换矩阵。
ωc=B-1ω
(36)
(37)
为求解保持架动力学微分方程,需联合滚动体运动微分方程进行求解,在惯性圆柱坐标系中列滚动体运动微分方程
(38)
(39)
式中:Mrj为滚动体质量惯量矩阵;δrj={rjθj}T为位移列向量;Frj为外载荷列向量;Fej为滚动体离心力。
2 计算结果与分析
根据对脂润滑圆锥滚子轴承动力学模型的分析,以圆锥滚子轴承ZWZ352226为例,保持架为内圈引导,材料为聚酰胺(尼龙66)。采用四阶Runge-Kutta法在MATLAB上实现对保持架和滚动体瞬态响应的求解,轴承外套圈固定,内套圈转动,各组件的位移、速度和载荷等初始值则通过轴承拟动力学分析模型得到,以保证求解结果的收敛和准确。润滑脂选用国产聚脲脂[18],主要流变参数(30 ℃):屈服应力τy=351.8 Pa,塑性黏度φ=8.44 Pa·sn,黏压系数α=4.662×10-2mm2·N-1,塑性指数n=0.719 6,锥入度λ=33.5 mm,润滑脂填充量为轴承内部空腔体积的1/6。
与圆锥滚子轴承保持架相比,滚动体的径向运动微乎其微,因此可忽略不计。考虑保持架为内套圈引导式,在径向载荷为21 kN,轴向载荷为10 kN,内圈转速2 500 r/min时,分析保持架振动规律和与滚动体、引导套圈的接触动载荷,如图6和图7所示。
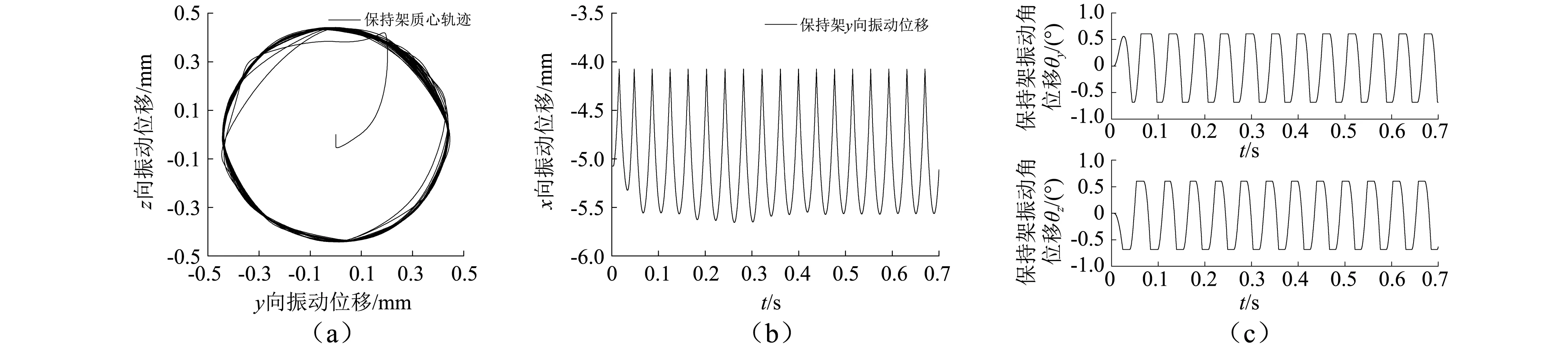
图6 保持架振动位移Fig.6 Cage vibration displacement
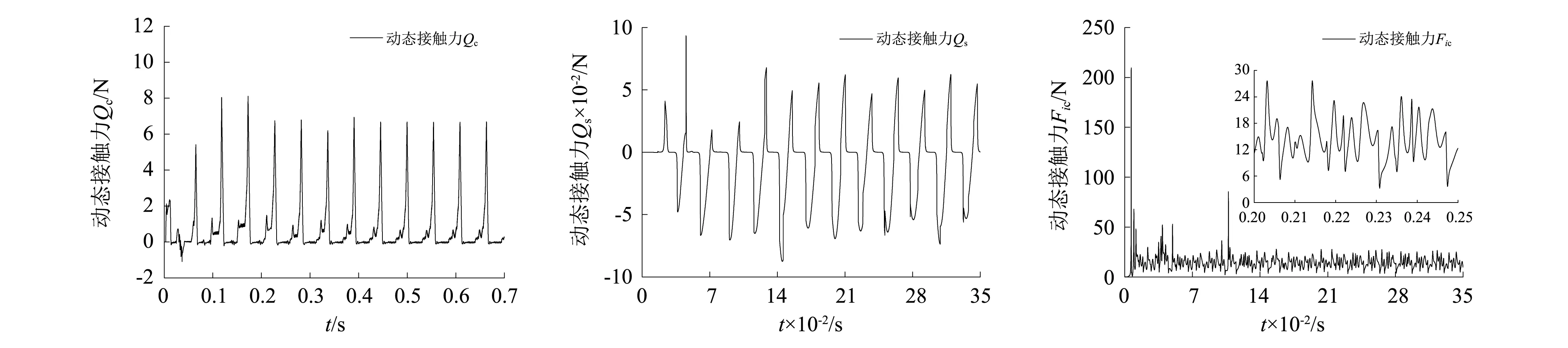
图7 保持架动态接触力Fig.7 Dynamic contact force of cage
由图6可知,保持架质心在径向平面内的运行轨迹近似为圆形,质心特殊轨迹的形成主要受引导边与保持架定心表面,以及保持架偏心离心力的影响;受兜孔内滚动体位置的限制,保持架质心沿轴线(o-x轴)呈现周期振动,并且兜孔侧梁与滚动体大端的相互作用频率要高。同样,受滚动体位置限制,保持架绕o-y轴和o-z轴也呈现周期性的角振动。由图7可知,在轴承运转过程中,保持架兜孔横梁与滚动体之间存在高频接触碰撞力,载荷呈现明显的冲击特征,保持架常见失效如横梁疲劳断裂,与这种高频接触碰撞有直接关联;对比兜孔横梁与滚动体的接触力,侧梁与滚动体的接触力要小得多,考虑梯形兜孔的结构特征,可推断保持架在径向平面内的偏转主要受兜孔横梁接触力的影响,因此下文主要针对兜孔横梁接触力进行分析。相较于滚动体对保持架的作用,内套圈引导面对保持架定心表面的高频作用要大得多,在实际应用中,通常保持架与引导套圈之间的磨损,要比滚动体与兜孔之间的摩损要严重。
由图8可知,保持架角速度在开始时震荡幅度较大,这时与滚动体的冲击作用较严重,在进入平稳阶段后,保持架与滚动体之间仍存在高频接触作用,但振动幅值变小并趋于稳定。滚动体公转转速在开始时振动幅值也较大,在转入平稳运行阶段后,振动幅值减小,但比保持架的振动要剧烈,结果均表明保持架与滚动体在轴承运转时转速并不稳定。
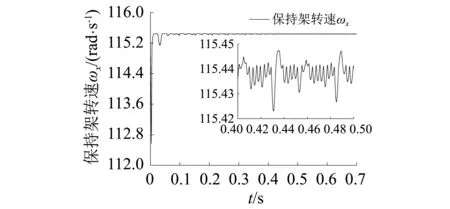
(a)保持架
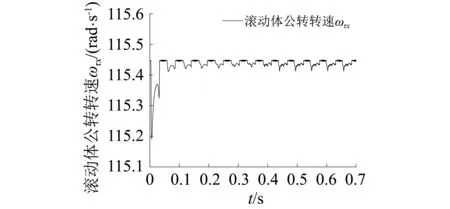
(b)滚动体图8 保持架和滚动体转速Fig.8 The rotational speed of cage and roller
圆锥滚子轴承各组件之间的动态接触力是影响轴承失效和稳定性的重要因素,也是轴承设计需考虑的关键因素之一。如图9所示,在径向载荷为21 kN,轴向载荷为10 kN时,分别使轴承内圈转速为4 000r/min,5 000 r/min,6 000 r/min,分析转速对保持架动态接触力的影响。
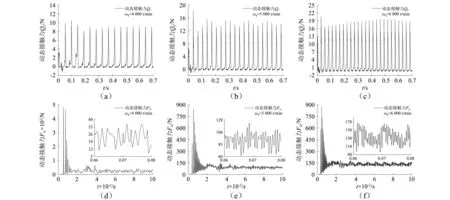
图9 保持架动态接触力Fig.9 Dynamic contact force of cage
由图9可知,保持架兜孔横梁与滚动体的动态接触力和接触频率随轴承转速的提升而增加,冲击载荷也会随之增加。从动态接触力的方向可知,在轴承运转过程中,主要是由滚动体推动保持架转动,这是由于轴承内腔润滑脂与空气的混合物对保持架表面的黏滞阻力矩作用,使得在滚动体公转方向的兜孔横梁与滚动体的接触作用频率更高。同样,内套圈引导面对保持架定心表面的作用力和作用频率也随着转速的提升而增加,且接触力幅值在开始阶段要远高于平稳阶段。当转速从4 000 r/min升高到6 000 r/min时,平稳阶段的接触力平均值由23.059 N增加到131.603 N,因此,轴承转速对动态接触力的影响不容忽视。
保持架和滚动体打滑都会影响轴承的服役性能,严重时会造成轴承异常振动、噪音、磨损和烧伤等,保持架和滚动体打滑率为
Sc=(ωg-ωx)/ωg×100%
(40)
Sr=(ωg-ωr)/ωg×100%
(41)
式中:ωr为滚动体公转转速。
在同一载荷条件下,分析转速对保持架和圆锥滚动体打滑率的影响,如图10所示。由分析结果可知,随转速增加保持架和滚动体的打滑率增大,保持架打滑率变化频率随转速的增加而降低,滚动体打滑率的变化频率则随转速的增加而增。随着轴承转速的增加,保持架偏心运动将会加剧,且滚动体离心力和陀螺力矩也增大,使得保持架和滚动体的打滑率增加,不利于轴承性能的维持。
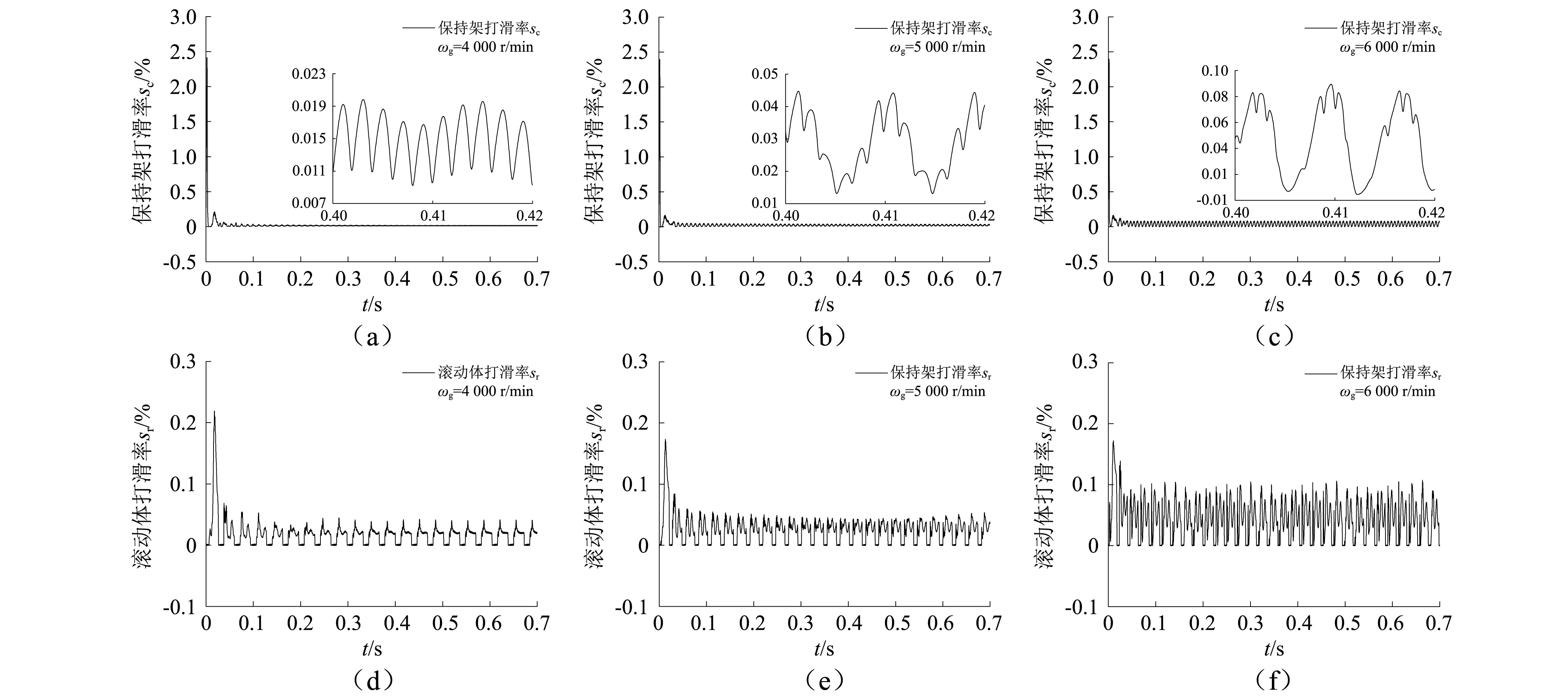
图10 转速对保持架和滚动体打滑率的影响Fig.10 The influence of speed on cage and roller slippage
根据上述分析,应尽量减小或避免保持架和滚动体的打滑运动,通常轴承打滑出现在轴承非承载区和高速轻载的工况下,说明载荷对保持架和滚动体的打滑也具有重要影响。如图11所示,在轴承转速为4 500 r/min,径向载荷分别为8 kN,14 kN,20 kN时,分析载荷对轴承打滑率的影响。从图11中结果可以看出,随径向载荷增加,保持架和滚动体的打滑率均明显降低,在径向载荷为8kN时,打滑率在经过一段时间后才进入平稳阶段。在分析过程中发现,当载荷小于8 kN时,打滑率甚至会达到20%以上。为解决滚动体和保持架的打滑问题,通常在轴承装配时会增加一个轴向预紧量,通过轴向预紧来改善轴承载荷分布。
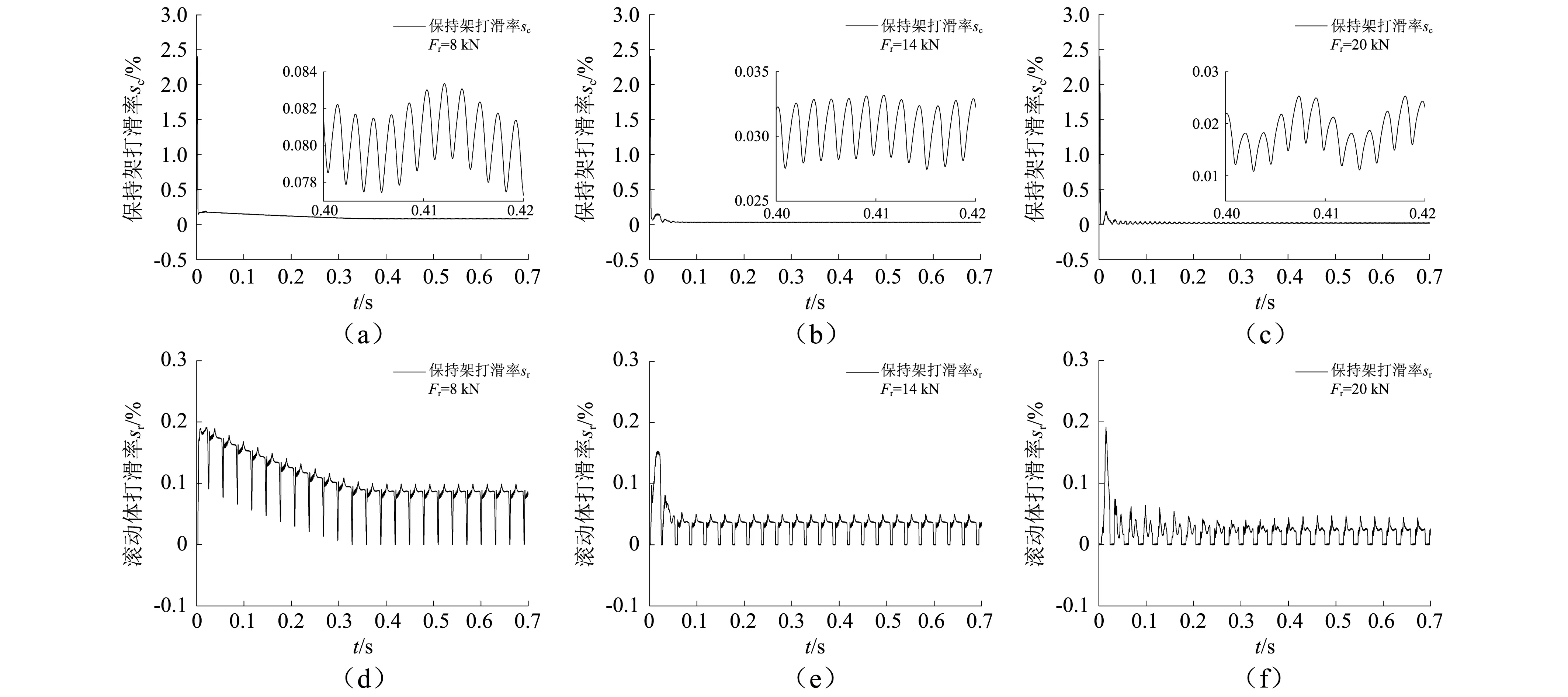
图11 载荷对保持架和滚动体打滑率的影响Fig.11 The influence of load on cage and roller slippage
如上述分析,圆锥滚子轴承轴向预紧是保证轴承使用性能的重要途径之一。如图12所示,在径向载荷为21 kN,轴向载荷为10 kN,转速为5 000 r/min时,分别使轴向预紧量为5 μm,15 μm,25μm,分析保持架打滑率随预紧量的变化规律。由图12可知,保持架打滑率随预紧量的增大而减小,在平稳阶段,当预紧量增加到25 μm时,打滑率最大幅值由0.025%减小到0.015%,其中随预紧量增大,承载滚动体个数从9个增加到15个(滚子总数为17个),也表明承载滚动体个数对保持架打滑率有重要影响,承载滚动体个数越多,保持架运行越平稳。预紧量的增加显然有助于减小保持架打滑率,但预紧量的过大势必会降低轴承使用寿命,因此在满足轴承寿命和使用要求的前提下,合理预紧量的选取十分重要。
圆锥滚子轴承保持架兜孔间隙Δδ和引导面间隙Δh′的确定是轴承设计的重要环节,间隙大小影响保持架与轴承各组件的润滑状态以及保持架运行的平稳性,仅考虑兜孔间隙或引导面间隙变化,在径向载荷为21 kN,轴向载荷为10 kN,转速为3 500 r/min时,分析间隙对保持架运转稳定性的影响,如图13所示。
由图13可知,随兜孔间隙增加,质心运动轨迹变宽,轨迹的无规律跳动也更明显,说明保持架运行的有序性和稳定性降低,同时,随兜孔间隙增大兜孔接触力也增大,在开始运转后0.2 s内的兜孔平均作用力由1.207 N增加到2.415 N。随着引导面间隙的增大,保持架质心运动轨迹的重叠率增加,轨迹变窄,平稳性增加,但保持架与引导面之间的接触作用力由51.095 N增加到139.828 N,因此对于引导面间隙的设计需要综合考虑保持架的稳定性和接触力等因素。
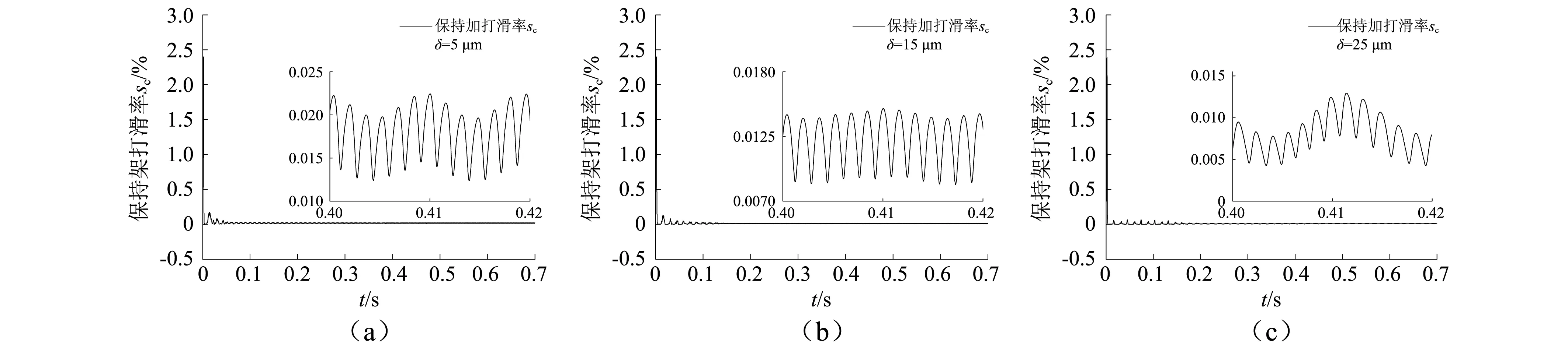
图12 预紧量对保持架打滑率的影响Fig.12 The influence of preload on cage slippage
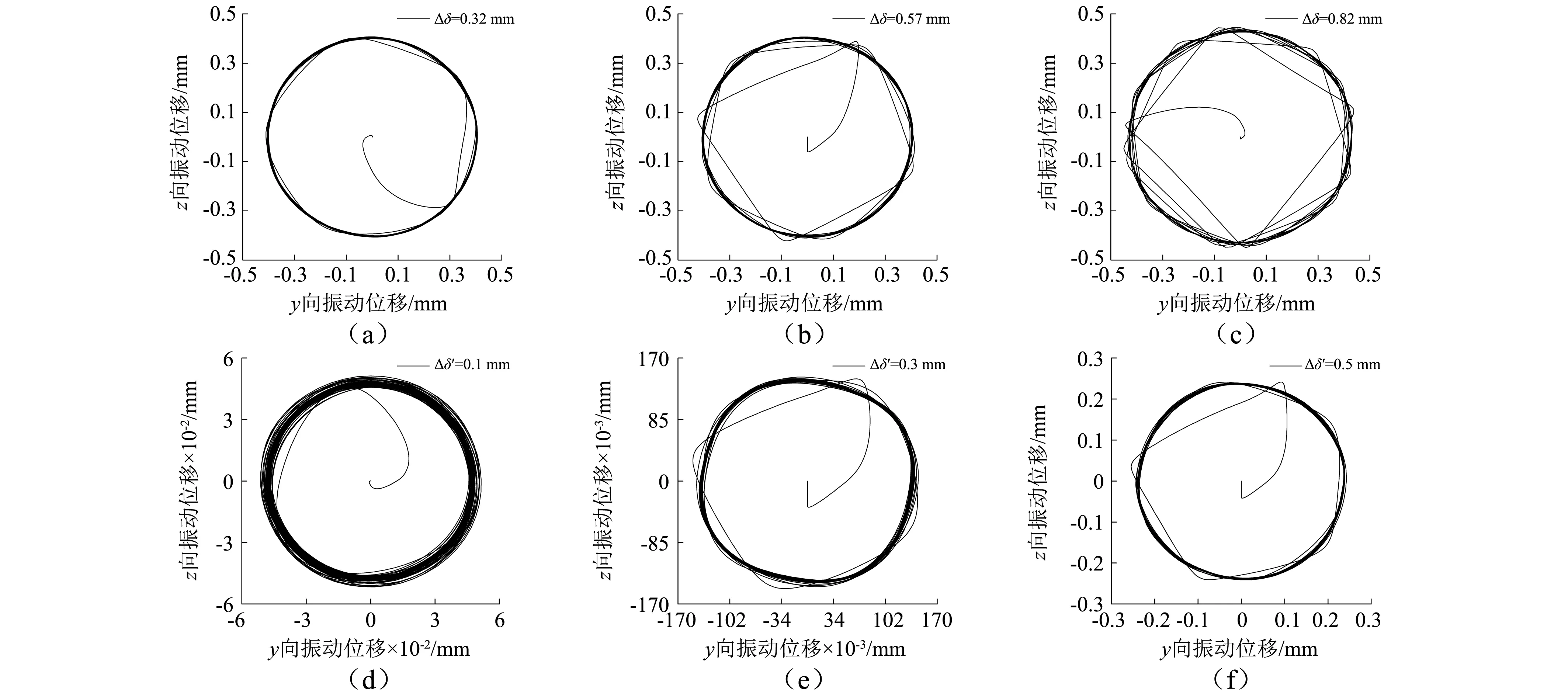
图13 间隙对保持架运行稳定性的影响Fig.13 Influence of clearance on cage stability
通常根据轴承的服役工况,对选取不同的保持架材料,圆锥滚子轴承保持架材料除聚酰胺外,一般还选取钢或铜材料,由于各材料的密度和力学特性均不相同,因此保持架的动体学特性也将有所差异,在径向载荷为21 kN,轴向载荷为10 kN,转速分别为1 000 r/min,3 000 r/min,5 000 r/min时,分析不同转速下各材料保持架运行的动态稳定性,如图14所示。
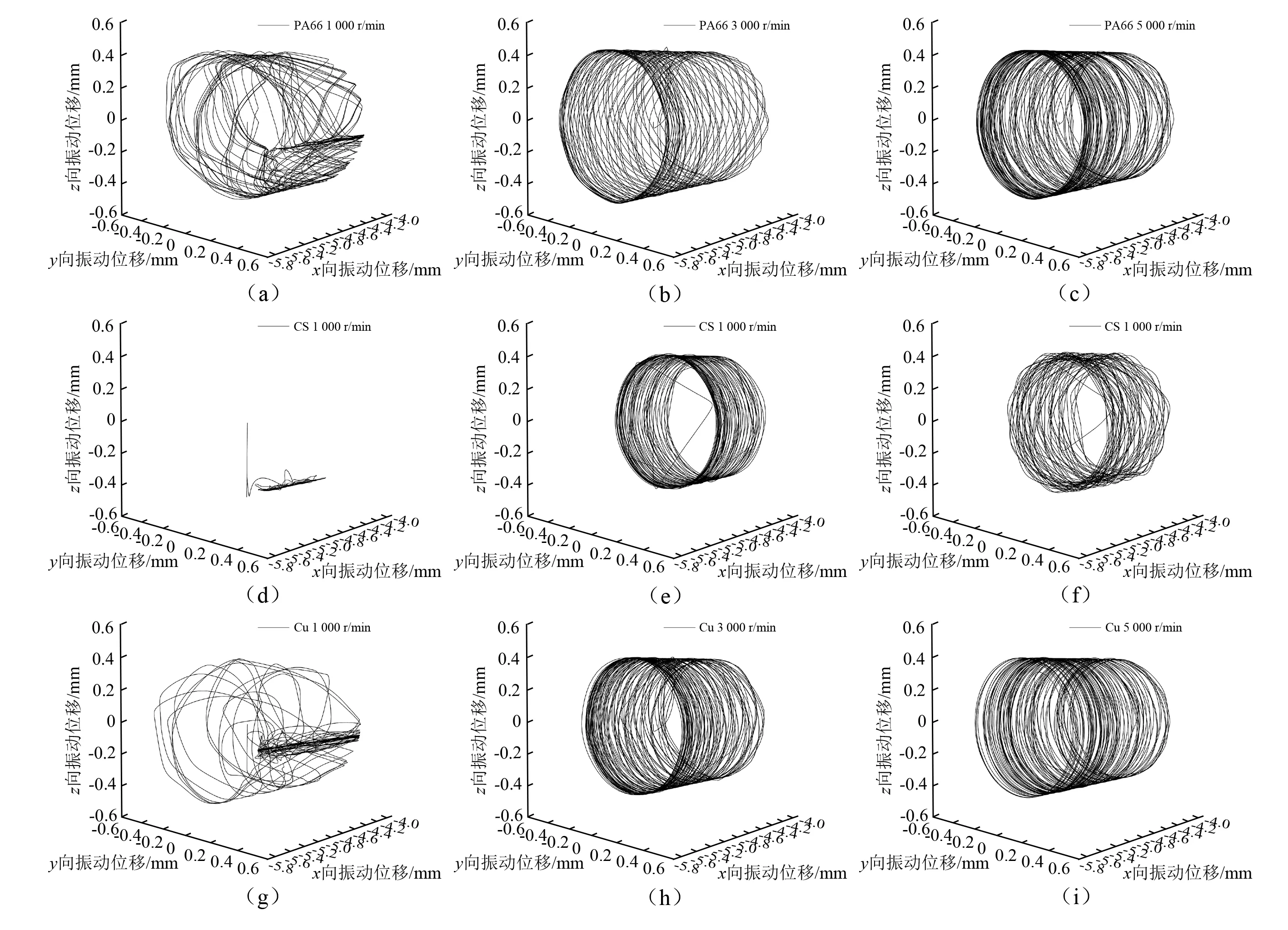
图14 三种材料保持架的质心空间运动轨迹Fig.14 The space motion track of cage mass center for three materials
图14可知,随着轴承转速的提高,三种材料保持架的运行平稳性也逐渐提高,在速度较高时,质心运行轨迹均类似 “圆筒状”,在低速时,保持架质心的运行轨迹均较为紊乱,稳定性差。其中,尼龙保持架的径向振幅相较于其他材料保持架最大,随转速增加到5 000 r/min,运行轨迹趋于紧凑,轴向窜动也相应减小;对于钢材料保持架,运行轨迹在3 000 r/min时十分紧凑和平稳,但随转速增加,运行轨迹在5 000 r/min时出现紊乱迹象,在转速变化范围内,钢保持架的轴向窜动最小;对于铜材料保持架,其轴向窜动随转速增大而增加,但整体平稳性和尼龙材料保持架类似。在圆锥滚子轴承设计中,根据实际工况对保持架的动态稳定性、抗冲击、耐磨性和耐腐蚀性能的要求,需综合各因素选取最合适的保持架材料。
3 结 论
本文分析了脂润滑状态下圆锥滚子轴承保持架的多体接触关系,建立了保持架全动力学模型,得到如下结论:
在平稳运转状态下,保持架与引导套圈接触作用力要远高于兜孔接触力,且保持架打滑率要低于滚动体打滑率;保持架和滚动体打滑率随轴承转速升高而增加,随载荷或预紧量的增加而减小。
滚动体与保持架兜孔间隙越小保持架动态稳定性越好,且兜孔接触力也越小;保持架定心面与内套圈引导面的间隙越小,定心面与引导面的接触力越小,但保持架稳定性变差;
当转速从1 000 r/min增加到5 000 r/min时,尼龙和铜材料保持架的动态稳定性增加,在转速为5 000 r/min时钢保持架的稳定性要次于尼龙和铜保持架。

