斜槽式超声变幅杆纵扭特性研究
张巧丽,张建富,冯平法,2,郁鼎文,吴志军
(1.清华大学 机械工程系,北京 100084;2.清华大学 深圳研究生院 先进制造学部,广东 深圳 518055)
材料科学的发展使得高性能光学材料、新型复合材料等广泛应用于机械、电子、航天、军事等领域。这些材料具有优异的物理性能和力学性能,如高强度、耐磨损、耐高温、密度小等。但由于这类材料硬度大、脆性强,加工时易出现刀具磨损严重、加工缺陷较多、加工效率低下等问题。众多研究表明,利用旋转超声加工方式加工此类材料,能有效降低切削力,减少加工缺陷,减轻刀具磨损[1]。
旋转超声加工是在工具高速旋转的同时辅以超声振动,如纵向振动和扭转振动。目前纵向振动旋转超声加工研究较多,且已经在生产实际中得到了广泛应用。近年来,国内外学者通过对比研究纵扭复合旋转超声加工与纵向振动的旋转超声加工的工艺特点,表明纵扭复合超声加工工艺效果更好。2010年,Cardoni等[2]研究了纵扭复合超声振动辅助岩石钻孔工艺,利用斜槽式模式转换方法获得扭转振动并与无斜槽纯纵向振动辅助加工工艺对比,得出纵扭复合超声振动辅助岩石钻孔的加工效率是纵向振动模式的四倍。2014年,Xiang等[3]等研究对比了纵扭复合超声振动辅助磨削与纵向超声磨削SiCp/Al复合材料的切削力,试验结果表明在相同加工条件下,纵扭复合超声振动辅助磨削产生的切削力比纵向振动磨削显著降低。2015年Asami等[4]试验比较了纵向超声振动与纵扭复合超声振动两种超声钻孔工艺的特征,试验表明相对于纵向振动,复合振动加工中切削力更小、效率显著提高、加工质量更好。基于以上研究可知,纵扭复合超声振动的工艺效果优于纵向振动,具有一定的研究意义。
斜槽式模式转换是实现纵扭复合振动的有效方式,也是目前国内外学者研究纵扭复合振动超声加工工艺的选择。1999年,林书玉[5]利用机电等效电路方法分析了斜槽角度对传振杆谐振频率的影响规律,实现了谐振频率的预测。2008年,皮钧[6]从应力波反射作用原理出发,研究纵波经斜槽反射后的应力状态,推导出斜槽角度与斜槽距离对纵扭振动转换的影响。2011年,Asami等[7]研究了压电纵扭复合振动换能器,利用斜槽结构实现纵扭模式转换,并通过试验探究了斜槽位置、角度、深度、斜槽数量等对纵扭振动幅度的研究。2013年,Liu等[8]基于数值分析法研究结构参数对变幅杆谐振频率的影响,设计出目标超声频率的斜槽式超声纵扭复合变幅杆。2016年,刘武等[9]通过有限元方法研究了斜槽结构参数对超声振动系统谐振频率的影响,发现斜槽长度和深度对谐振频率影响最大。2016年,袁松梅等[10]基于有限元分析方法研究振动系统结构参数对纵振和扭振谐振频率的影响,实现了纵向和扭转的谐振频率简并。此外,陈建毅[11-13]还研究了双斜槽结构对扭振输出的影响以及在圆锥面上开螺旋槽的扭振特性。
斜槽式结构的局限在于没有成熟的目标频率设计理论,难以实现纵扭复合,且纵扭转换效率低下,输出扭振振幅小。国内外目前研究多为如何实现目标频率设计实现,在提高模式转换效率方面研究较少。本文从超声波斜入射理论出发,研究超声波模式转换原理;提出振幅比值这一指标来量化模式转换效率,利用有限元仿真方法研究不同斜槽结构对模式转换效率的影响;最后基于结构优化设计出台阶式变幅杆进行试验,实现了较大的扭振振幅输出。
1 斜槽式超声变幅杆设计理论
斜槽结构在超声波传导过程中能将部分纵振波(纵波)转换为扭转波(横波),实现波的模式转换。斜槽结构将正应力转换为切应力,从而引起扭转振动。其模式转换原理可用超声波斜入射理论来解释,即当一束超声波以一定倾斜角达到两种材料的界面时,界面处将发生波形转换。入射能量被分成几种不同的超声波能量。将入射波考虑为以倾斜角θ作用在界面上的力,该力在界面处产生非常复杂的波动。这种复杂的波动可以看作是两种独立振动的叠加:一种是与法向力相关的纵波传播;另一种是与切向力相关的横波传播[14]。

图1 固-固界面的反射与折射Fig.1 The reflection and refraction between solid-solid interface
如图1所示,一纵波入射到固-固界面(y=0)。根据Snell定律,角度满足式(1)
(1)
假定结合面为理想结合面:各向同性介质1和各向同性介质2在坐标系XYZ中是两个半无限空间,质点速度V和应力σij在y=0处满足连续条件,如式(2)

(2)
式中:VN为入射波质点速度;V1L,V1T分别为反射纵波、横波的质点速度;V2L,V2T分别为折射纵波、横波的质点速度,其表达式如式(3)
(3)
式中:Ai(i=N,1L,1T,2L,2T)为波的振幅;ki(i=N,1L,1T,2L,2T)与波长的倒数成正比。对于各向同性介质中的二维平面应变问题,已知质点的速度-位移关系如式(4)所示,应变-位移关系如式(5)所示,应力应变关系如式(6)所示。
(4)
(5)
(6)
由式(4)~式(6)可得式(7)
(7)
式中:λ和μ为材料的拉梅常数,满足式(8)
λ+2μcos2αL=(λ+2μ)cos(2αT)
(8)
将式(7)和式(8)代入连续条件式(2),可得到反射系数方程

(9)
式中:RL,RT,DL,DT分别为纵波反射系数、横波反射系数、纵波折射系数、横波折射系数,即对应波形与入射波的振幅之比;
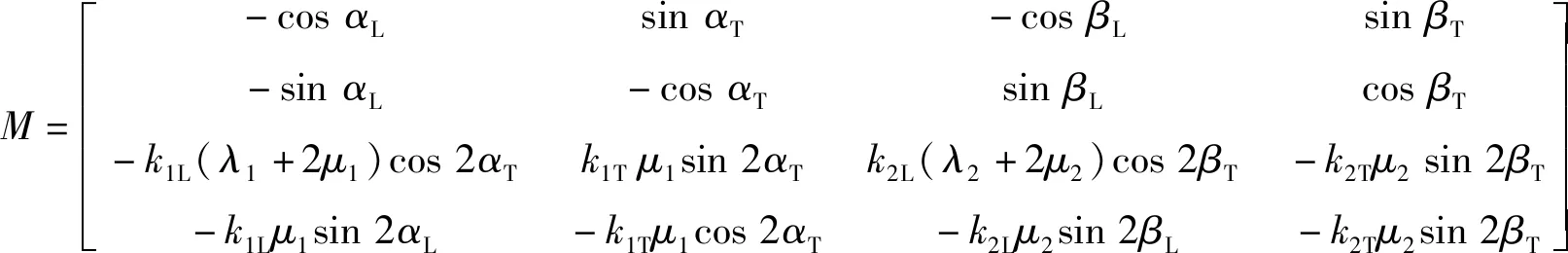
(10)
对纵波入射,有
(11)
式(9)的反射系数方程适用于固-固界面。若入射截面为固-液或固-气界面,则由于液体或气体中不存在横波,切向速度连续条件不存在,即不存在横波折射系数。
(12)
(13)
根据以上公式,可以计算出钢-空气界面纵波入射情况下反射系数随入射角的变化规律,如图2所示。
斜槽式超声变幅杆的设计利用了超声波的斜入射原理,将入射的部分纵波转换为横波,实现杆的扭转振动,如图3所示。一部分纵波入射到斜槽端部,发生垂直反射;一部分纵波入射到斜槽表面,发生了回反射现象,即波向输入端传递;一部分纵波进入斜槽区域,进行多次反射,实现模式转换;若斜槽间隙过大,部分纵波会不发生反射,直接传递到输出端。垂直反射、回反射和不反射现象均会降低模式转换效率。在斜槽结构设计中,需要通过结构设计尽量减少回反射、垂直反射和不反射。对于入射到斜槽区域的纵波,由图3可知,模式转换过程中存在多次反射,根据斜入射理论,可以计算出二次反射后纵波和横波相对入射纵波的振幅比,如图4所示。从图中可知,二次放射后纵波振幅与入射波振幅比值(RL2)恒为1,则横波振幅与入射波振幅比值(RT2)即为横波振幅与纵波振幅的比值。因此在模式转换过程中,存在最佳入射角,使得输出的横波和纵波的振幅比值最大,即模式转换效率最大。
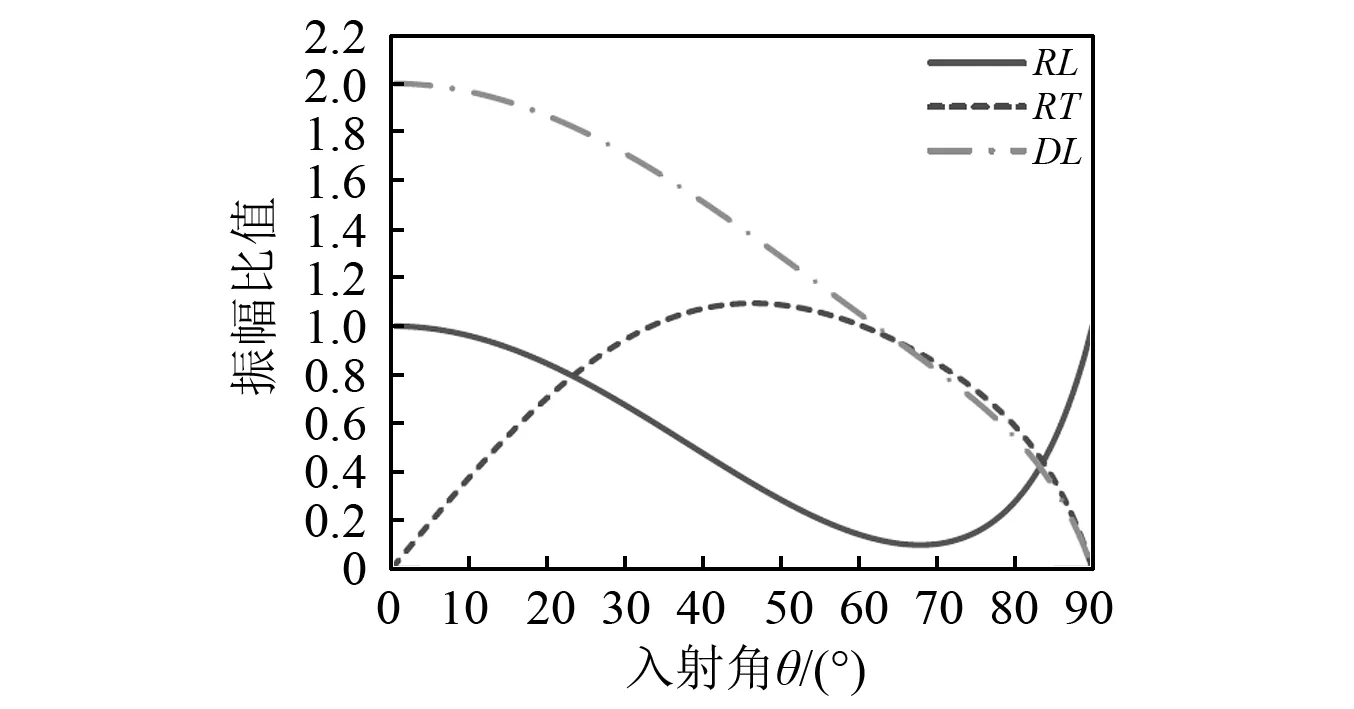
图2 纵波斜入射到钢-空气界面上的反射系数Fig.2 The reflection and refraction of incident longitudinal wave between steel-air interface

图3 斜槽式模式转换示意图Fig.3 Schematic diagram of wave conversion with slanting slots

图4 纵波入射斜槽经二次反射后的振幅比值Fig.4 Amplitude ratio of incident longitudinal wave after re-reflection
2 斜槽结构参数对纵扭特性的影响规律研究
超声波斜入射理论解释了模式转换的原理。根据理论计算可知:理想界面情况下,存在最佳入射角,使得纵波入射的模式转换效率最大。超声变幅杆上的斜槽设计实现了纵扭振动的模式转换,其转换效率除了与斜槽角度有关,还与斜槽宽度,斜槽个数,斜槽深度以及斜槽长度等有关。因为在纵波传递过程中,存在垂直反射和回反射,降低了模式转换效率,如图3所示。
本文基于ANSYS Workbench有限元分析软件利用谐响应分析法仿真不同斜槽结构的变幅杆在其谐振状态下的纵扭转换效率。纵扭转换效率以输出端的扭振振幅和纵振振幅之比来表征,即为振幅比率R。仿真模型如图5所示。为减弱变幅杆结构特征对纵扭转换效率的影响,仿真模型为圆柱形传振杆,且开槽位置为杆的中心处。槽的形状为扇形槽,保证了在每一圆柱面上斜槽角度一致。且以槽的扇形角度来表示斜槽宽度,如图6所示。斜槽角度即为螺旋角。仿真模型各个结构参数数值如表1所示 。
2.1 斜槽角度
根据斜入射分析可知,入射角度是影响模式转换比率的重要因素。对于纵波入射,入射角接近0°或90°时,反射波中横波比例较低。斜槽角度指的是槽的螺旋角,与纵波入射角互余。根据图4可知,最佳入射角约为30°,即最佳斜槽角度约为60°。基于有限元方法仿真得斜槽角度A与振幅比率R的关系,如图7所示。改变斜槽个数、宽度参数,斜槽角度与振幅比值关系曲线规律不变。存在最佳斜槽角度,使得振幅比值最大;改变其他结构参数,最佳斜槽角度值较为稳定,约为52°。实际仿真值低于理论值,这主要是因为过大的斜槽角度会增加纵波的回反射,降低模式转换效率。

图5 有限元仿真模型Fig.5 Model of finite element simulate

图6 仿真模型参数示意图Fig.6 Schematic diagram of parameters on the model of finite element simulate

表1 仿真模型结构参数Tab.1 Structural parameters of simulation model
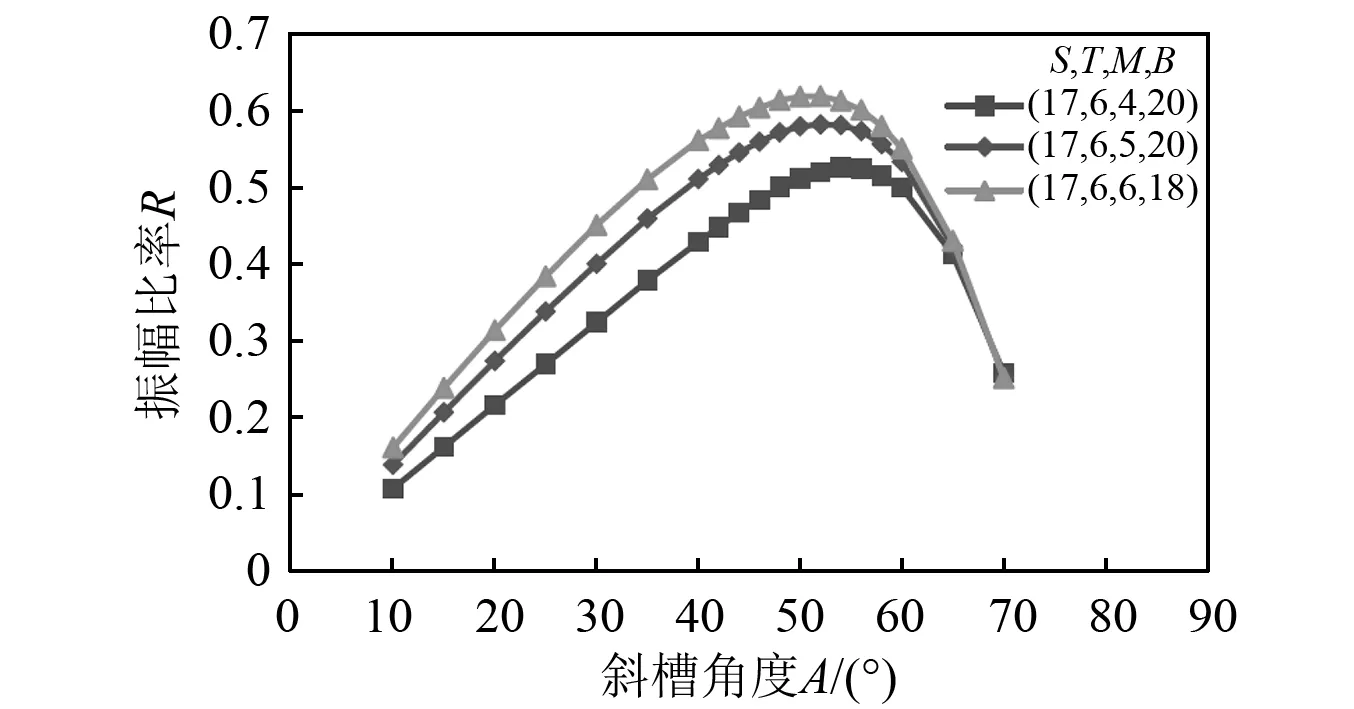
图7 斜槽角度与振幅比率之间的关系Fig.7 The relationship between angle of slanting slots and amplitude ratio
2.2 斜槽个数与斜槽宽度
斜槽宽度以扇形槽对应的圆心角角度来表示。斜槽参数的数值相对独立,即不依赖斜槽的深度,也不依赖圆柱半径。在不同斜槽个数情况下,改变斜槽宽度,有限元仿真求解传振杆输出端在谐振状态下振幅比率R,如图8所示。当斜槽个数确定时,存在一个最佳斜槽宽度B,使得纵扭振幅比最大,即模式转换效率最高;最佳斜槽宽度随斜槽个数增大而减小;斜槽个数的增加能够明显提高模式转换效率。

图8 斜槽宽度与振幅比率之间的关系Fig.8 The relationship between width of slanting slots and amplitude ratio
斜槽宽度的增大能减小相邻斜槽间隙,减少回反射,增加纵波反射次数,提高模式转换效率;但是也会带来垂直反射的增加,从而降低模式转换效率。综合两方面的因素,存在最佳斜槽宽度使得模式转换效率最大。斜槽个数的增大能明显减小相邻斜槽间隙,对模式转换效率的改善较为明显。当斜槽个数增大后,垂直反射也会增加,可通过减小斜槽宽度来保证较好的模式转换效率,因此最佳斜槽宽度随斜槽个数增大而减小。
在实际应用时,我们可以选择尽可能大的斜槽个数以实现最大模式转换效率。但由于斜槽个数的增大将导致最佳斜槽宽度减小,工艺实现难度增大,我们在选择斜槽个数时也应考虑最佳斜槽宽度的大小。
2.3 斜槽深度
斜槽深度指扇形槽的径向长度。在波的传递过程中,中心部分纵波不经过任何反射,可直接传递至输出端。增大斜槽深度,可以减少不反射的纵波比例,明显增加模式转换效率。随着斜槽深度的增加,上升趋势会变缓。
利用有限元仿真方法获得不同参数下斜槽深度与振幅比率R的关系曲线,如图9所示。随着斜槽深度的增加,纵扭振幅比率明显上升,在曲线中间部分基本上呈线性相关关系。但当斜槽深度达到8 mm时,曲线趋于平稳。斜槽是扇形结构,当斜槽深度较大时加工较为困难,应用时应选择合适的斜槽深度。

图9 斜槽深度与振幅比率之间的关系Fig.9 The relationship between depth of slanting slots and amplitude ratio
2.4 斜槽长度
斜槽长度是指斜槽区域在轴线方向上的长。利用有限元仿真获得斜槽长度与振幅比率的关系,如图10所示。当斜槽长度较小时,除了传振杆中心区域纵波可以不经任何反射传递到输出端,传振杆外层部分纵波也可以不经过任何反射传递至输出端。此时斜槽长度的增大能够明显减少不反射纵波比例,快速提高模式转换效率。当斜槽长度增加到一定值时,传振杆外层部分不存在不反射纵波,斜槽长度的增大仅是增加模式转换过程中纵波反射次数,对模式转换效率的提高较为缓慢,故图中曲线最后涨幅逐渐减小并趋于稳定。实际设计时斜槽长度的值选择趋于稳定的临界值即可。

图10 斜槽长度与振幅比率之间的关系Fig.10 The relationship between length of slanting slots and amplitude ratio
3 试验研究
3.1 试验方法
为验证上文提出的仿真方法的有效性,基于仿真得到的各结构参数对纵扭振幅比率的影响规律,本文设计制造了具有斜槽结构的阶梯式变幅杆,斜槽参数如表2所示。有限元仿真圆柱传振杆斜槽区域与输入端距离对振幅比值的影响,如图11所示。当斜槽区域接近输入端时,振幅比值较大。为实现与换能器的匹配,以达到谐振,设计时需对变幅杆的台阶面位置调整,使变幅杆在20 kHz 附近谐振。变幅杆采用螺纹连接方式,装配在自行研制的超磁致伸缩换能器上,如图12所示。

表2 变幅杆结构参数Tab.2 Structural parameters of the horn

图11 斜槽位置与振幅比值的关系Fig.11 The relationship between position of slanting slots and amplitude ratio

图12 超声振动系统(换能器+变幅杆)Fig.12 The ultrasonic vibration system
试验中先采用阻抗分析仪(PV80A,Bandera,中国)测量超声振动系统的谐振频率和补偿电容,再利用超声电源(BP4610,NF,日本)的扫频功能确定实际电压激励下的谐振频率。振幅测量由激光位移传感器(LK-H008,Keyence,日本)来完成,试验装置如图13所示。

图13 实验装置Fig.13 The experimental device
超声振动系统的纵向振幅由变幅杆输出端面测量。为测量扭振振幅,在变幅杆输出端铣削出两个侧平面,如图14所示。系统扭转振动角度振幅θ与侧平面测量振幅X满足式(14)
(14)

图14 侧平面扭振测试原理Fig.14 The principle of testing the torsional vibration
由于扭转振动角度振幅θ是小量,cosθ≈1 ,tanθ≈θ,则式(14)可简化为
(15)
则扭转振幅可表示为
(16)
式中:R为圆柱半径;Y为测点高度。
3.2 试验结果
首先利用阻抗分析仪寻找振动系统的谐振点。阻抗圆如图15所示,振动系统的谐振频率为19 580 Hz,补偿电容为93.4 nF。由于超声系统的谐振频率随激励电压变化会有所漂移,确定激励电压后,仍然需要用电源的扫频功能确定系统的谐振频率。试验中超声电源采用120 V电压激励超声振动系统,扫频范围19 430~19 560 Hz,步距为10 Hz。激光位移传感器采样频率为200 kHz,测试结果如图16所示。根据测试结果可知振动系统实际谐振频率为19 500 Hz。在实际测量中,激光位移传感器的测量受外界影响较大,测量数据存在较大的波动。因此基于Matlab软件设计了数字带通滤波器,其幅频特性如图17所示。滤波前后数据对比如图16所示。
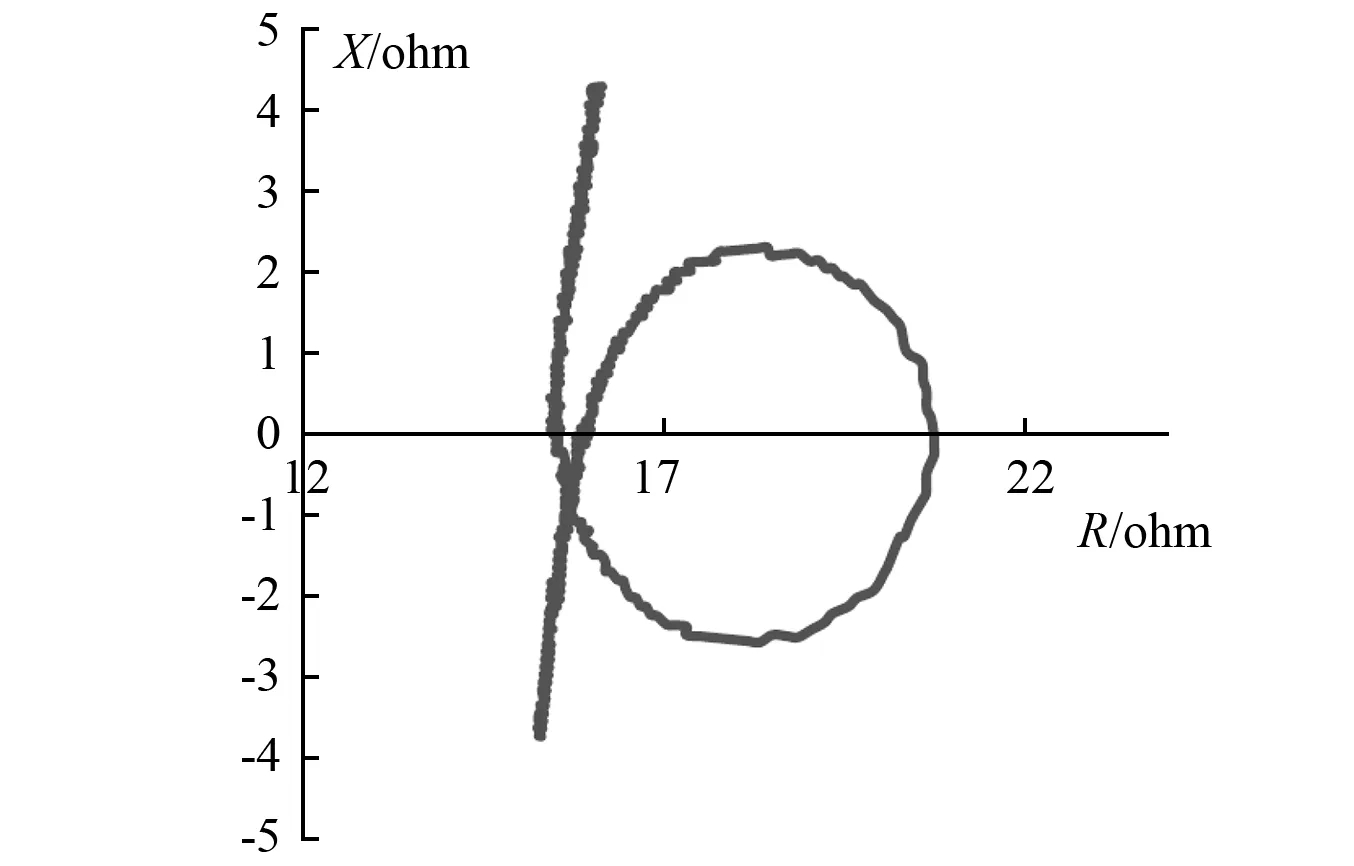
图15 振动系统阻抗分析Fig.15 The impedance analysis of the vibration system

图16 激光位移传感器数据及滤波数据Fig.16 Data of the laser displacement sensor and data after filtering

图17 带通滤波器的对数幅频特性曲线Fig.17 The logarithmic amplitude-frequency curve of the band-pass filter
试验中对变幅杆端面和侧面分别测试三组数据,如表3所示。端面振幅即为系统纵振振幅,AL=9.5 μm;根据式(16),可将侧平面振幅转换为扭转振幅,R=5 mm,Y=2.5 mm,扭振振幅AT=29 μm。本试验验证了合理设计斜槽结构,可增大纵扭转换效率,输出大的扭转振动振幅。

表3 实验数据(滤波后)Tab.3 The experimental data after filtering
4 结 论
斜槽式模式转换实现纵扭复合振动的关键在于超声变幅杆斜槽结构参数的合理设计。本文首先基于超声波斜入射理论分析了模式转换的基本原理,即当一束超声波以一定倾斜角达到两种材料的界面时,界面处会发生波形转换,将入射的部分纵波转换为横波,从而实现杆的扭转振动。进而以纵扭振幅比率来量化模式转换效率,系统研究了斜槽角度、斜槽个数、斜槽宽度、斜槽深度和斜槽长度等关键结构参数对于纵扭模式转换效率的影响规律。结果表明:当斜槽角度为52°左右时,纵扭转换效率最大,且改变其他结构参数时最佳斜槽角度相对稳定;存在最佳斜槽宽度,使得纵扭转换效率最大;斜槽个数的增加能明显提升纵扭转换效率,且最佳斜槽宽度随斜槽个数增大而减小;斜槽深度和斜槽长度越大,纵扭转换效率越大,但达到一定长度值时趋于稳定。最后,基于仿真研究的结果,选取优化的结构参数设计了一种斜槽式阶梯式纵扭复合超声变幅杆,变幅杆一阶纵振谐振频率和二阶扭振谐振频率位于20 kHz附近,通过搭建的试验平台进行了试验研究,其振动系统输出的纵振振幅、扭振振幅分别为9.5 μm,29 μm。

