可控磁路式永磁悬浮系统的鲁棒控制
孙 凤,夏鹏澎,孙兴伟,金俊杰,赵文辉,窦汝桐,于慎波
(沈阳工业大学 机械工程学院,沈阳 110870)
可控磁路式永磁悬浮系统具有无发热、结构紧凑、磁力强等优点,主要用于无尘传送场合,避免传送装置的金属粉尘和油污对工作环境的污染[1]。系统由直流伺服电机、盘状径向磁化永磁铁、导磁体和导磁铁棒组成;其中,永磁铁提供磁力,电机驱动盘状永磁铁旋转,改变通过导磁体与导磁铁棒的磁通量,实现悬浮力大小的控制[2],与其他类型的磁悬浮装置相比,由于该系统的特点,导致在控制方面的难度系数有所增加。
在控制方法方面,磁悬浮系统的控制方案主要分为线性控制和非线性控制[3]。线性控制以悬浮系统在工作点处的线性化模型为基础,以PID(Proportion Integration Differentiation)控制[4-5]和状态反馈控制[6]为代表,具有结构简单、调节参数方便、参数易于整定,一定程度上可以使磁悬浮系统的控制精度达到要求,但适用性差,抗外扰力较弱。非线性控制主要包括模糊控制[7]、滑模控制[8]、自适应控制[9]等控制方案,提高了系统的鲁棒性,但稳定性较差。其不能很好应用到磁悬浮系统工程实践中的主要原因是理论设计的方法通常不考虑实际系统中的延时问题,试图以实际系统缓慢的输出来跟踪理论上跳变的设计值,而实际的控制器有时无法做到算法要求的实时性[10],这在永磁悬浮系统的控制结果上表现的更加明显。
考虑到该系统具有存在非线性、负载冲击扰动的特点,为了实现其跟踪位移输入、抑制冲击扰动,增加控制器的鲁棒性,稳定性,以及简化控制器的设计的目标。结合传统状态反馈控制的设计方法,基于LMI(Linear Matrix Inequality)的H∞鲁棒控制理论,设计了针对性较强的状态反馈γ-次优H∞鲁棒控制器,并对该系统进行基于MATLAB的悬浮仿真分析[11-12]以及试验验证,结果表明该控制器可使系统尽快消除外界和自身因素产生的扰动以及对输入信号的准确快速跟踪,具有很好的鲁棒稳定性。
1 系统悬浮原理及可行性分析
1.1 系统悬浮原理
可控磁路式永磁悬浮系统的模型,如图1所示,该系统主要由径向磁化的盘状永磁体、驱动该盘状永磁体的导磁体直流伺服电机、一对“F”型导磁体以及导磁悬浮物组成。其中,盘状永磁体选择顺时针方向为正方向。通过改变盘状永磁体的旋转角度,改变系统的磁路,达到改变导磁体和导磁悬浮物之间的吸引力(悬浮力)的目的。
1.2 系统悬浮可行性分析
图2为该系统基于有限元分析软件的2D分析结果。其中,图2(a)所示为盘状永磁铁的旋转角度转角θ=0°时,系统磁感线分布情况,从N极出发的磁感线没有通过磁性悬浮物,大部分磁感线通过导磁体直接回到S极,少量的磁感线通过空气回到S极,该部分通过空气的磁感线是由系统的漏磁所产生;图2(b)为盘状永磁铁的旋转角度转角θ=30°时,系统磁感线分布情况,从N极出发的磁感线一部分通过磁性悬浮物回到S极,一部分直接通过导磁体直接回到S极,少量的磁感线通过空气回到S极;图2(c)为盘状永磁铁的旋转角度转角θ=90°时,系统磁感线分布情况,从N极出发的磁感线全部通过磁性悬浮物回到S极,空气中基本上没有漏磁。
随着盘状永磁铁转角的增大,通过导磁悬浮物磁通量增大,导磁体与导磁铁棒之间的吸引力也随之增大,即二者之间悬浮力可以通过改变盘状永磁铁的转角的大小来控制。此外,该系统中永磁铁不直接提供悬浮力,驱动盘状永磁体直流电机的输入电流对悬浮物重量的变化不敏感,系统的功耗比较低。

图1 系统原理图Fig.1 The principle diagram of the system

图2 有限元分析结果Fig.2 The finite element analysis results
2 系统数学模型建立
系统模型图示及符号定义如图3所示,fm为导磁体与悬浮物之间的悬浮力;d为导磁体和悬浮物之间空气气隙;d0为在平衡状态时的空气气隙;z为在平衡状态时,悬浮物偏离选定的平衡位置的位移,方向向上,d=d0-z;θ为盘状永磁铁沿顺时针方向的旋转转角;D为盘状永磁体与导磁体之间的气隙长度。
通过前期试验可得到系统悬浮力以及盘状永磁铁转矩的数学模型分别如式(1)和式(2)所示
(1)
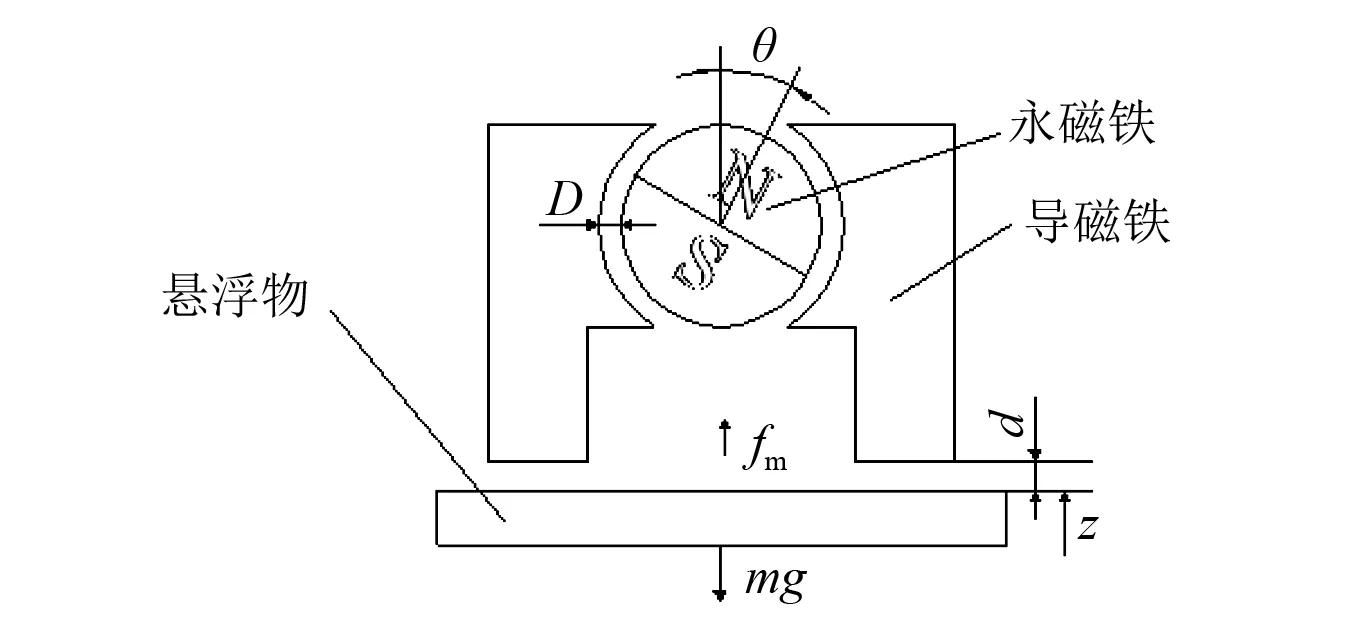
图3 模型符号定义Fig.3 Model symbol definition
(2)
式中:km为悬浮力系数;Δdf为悬浮力在盘状永磁体和导磁体气隙处的漏磁补偿系数;kτ为盘状永磁铁的转矩系数,选取顺时针方向为正方向;Δdτ为转矩在盘状永磁体和导磁体气隙处的漏磁补偿系数。
根据(1)和式(2),当系统受到外力时,系统的运动学方程可表达为
(3)
(4)
式中:J为电机和盘状磁铁的转动惯量,选取顺时针方向为正方向;kt为伺服电机转矩系数;i为驱动盘状永磁体旋转的伺服电机输入电流;m为悬浮物的质量;f为系统所受的外力扰动。
3 悬浮系统的鲁棒控制器设计
被控对象处于稳定悬浮状态,当吸引力随着盘状永磁铁转角增大而变大时,导磁体和铁棒之间的距离会减小。假设系统微小位移z的正方向向上,则在该平衡位置对吸引力和盘状永磁体的转矩进行线性化,可分别表示如式(5)和式(6)
(5)
(6)
式中:z,Δθ为偏离悬浮平衡位置的微小量;d0和θ0为平衡位置的值。
根据式(1)~式(6)可建立系统的状态方程为
(7)

其中,
在选定的平衡位置处,状态空间方程中的各变量具体数值如表1所示。

表1 系统结构参数Tab.1 The parameters of suspension system
系统的广义状态模型如图4所示,其中Δi=Kx,K为所设计的状态反馈γ-次优H∞鲁棒控制器
该系统要求对于任意干扰信号f∈L2,L2∈[0,+∞]均可以保持闭环控制系统稳定,即
(8)
式中:qi≥0,ρ>0 为加权系数。

图4 系统状态空间结构图Fig.4 The system state space structural diagram
定义评价信号为
(9)
则式(9)等价于‖z1‖2<γ‖f‖2。因此,设计系统γ-次优H∞鲁棒控制器的问题即转化为设计使闭环系统内部稳定且‖TZ1f(s)‖2<γ控制器的问题。其中,TZ1f(s)为从f~z1的最小传递函数。
根据式(7)和式(9)可得到广义系统的状态空间为
(10)
式中:A,B1,B2,C1,C2,D12为系统的输出矩阵;Δi为控制电流矩阵。
对于上述系统,若存在一个状态反馈控制器H∞鲁棒控制器,当且仅当存在对称矩阵X和W使其满足以下线性矩阵不等式(LMI),
(11)
且线性矩阵不等式存在一个可行解X*和W*,则K=W*(X*)-1即为所求系统的状态反馈γ-次优H∞鲁棒控制器,其可以使闭环系统保持稳定且具有一定的扰动抑制能力。在Matlab环境下建立式(11)的求解程序,选取不同的加权系数和迭代次数即可求得该状态反馈γ-次优H∞鲁棒控制器。
4 系统悬浮原理及可行性分析
4.1 位移跟踪仿真
采用表1中数据对系统进行仿真分析,分别对悬浮物偏离平衡位置的位移z、盘状永磁铁的旋转角度θ、输入电流i进行跟踪,得到结果如图5所示。悬浮物首先处于稳定悬浮状态,0.4 s时,在位移参考输入端加载0.07 mm的阶跃位移信号。此时,位移z将增大直至悬浮物达到新的平衡位置(稳定气隙减小);角度θ先增大然后减小直至达到新的稳定值,该值将小于初始值;电流i先减小然后增大直至达到新的稳定值。

图5 位移阶跃信号的跟踪仿真结果Fig.5 The simulation result of system with step signal track
仿真分析结果表明该控制器能够保证闭环系统稳定运行且可以快速响应参考输入。
4.2 外扰仿真
其他数据不变,在0.4 s时,将幅值为0.127 N、时间为0.1 s的脉冲力作用在悬浮物上,采用同样的控制器对系统进行仿真分析,得到结果如图6所示。在施加力时,位移z减小(稳定气隙增大),外力消失后,位移z开始增大直至回到平衡位置;角度θ先增大后减小直至回到平衡位置;电流i先减小然后逐渐增大直至回到稳定状态。
仿真分析结果表明该控制器具有很强的抑制外扰能力,可以使闭环系统在受到外扰的情况下保持稳定。
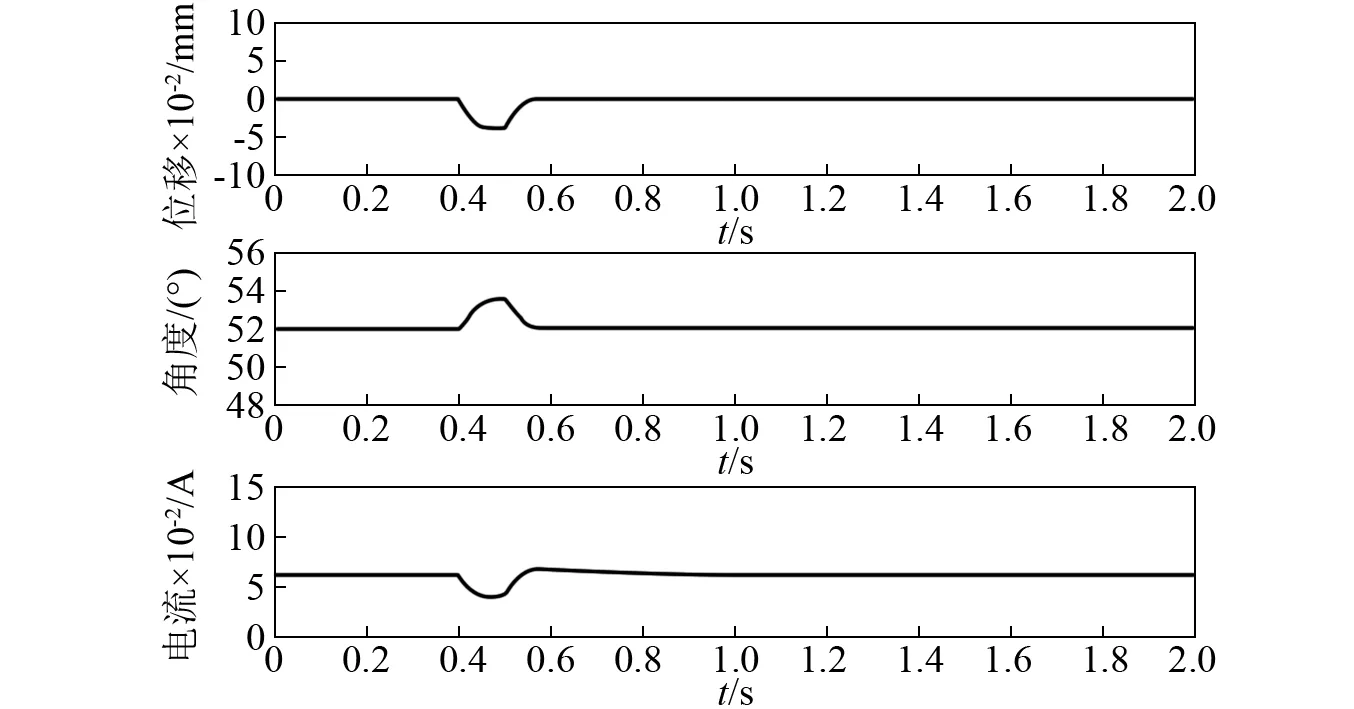
图6 系统受外力扰动时的仿真结果Fig.6 The simulation result of system with disturbance force
5 悬浮试验验证
5.1 试验平台
图7为单自由度磁悬浮控制系统,系统主要由上位机、dSPACE控制器、电涡流位移传感器、直流伺服电机和伺服电机驱动器组成。其中,单自由度磁悬浮试验平台,如图8所示(该图中悬浮物处于悬浮状态)。其中,“F”型导磁体位于盘状永磁体两侧;盘状永磁体通过联轴器与直流伺服电机相联接,直流伺服电机位于盘状永磁体背面;为了方便调节重量,悬浮物由多块导磁体组成,其与限位滑块通过螺栓连接在一起;滑块与直线导轨组成直线导轨副,用于平衡两个导磁体对悬浮物产生的不平衡转矩;电涡流位移传感器位于悬浮物正下方,用以测量悬浮物偏离平衡位置的位移,灵敏度为1 V/mm;悬浮物的平衡点气隙为6 mm;采用dSPACE为系统控制部件。此外,这里采用对位移信号和角度信号微分的方式,来间接获得另外两个状态量。

图7 单自由度磁悬浮控制系统Fig.7 Single degree freedom suspension control system

图8 单自由度磁悬浮试验平台Fig.8 Single degree freedom magnetic suspension experimental facility
单自由度磁悬浮控制系统工作原理,如图9所示,直流伺服电机驱动盘状永磁铁旋转,从而改变系统中通过悬浮物的磁通量,改变磁力;电涡流位移传感器采集的位移信号经过A/D转换传递到dSPACE控制器中,直流伺服电机编码器采集的角度信号也同样传递到dSPACE控制器中,通过运算输出伺服电机的控制信号,经过D/A转换以及驱动器,实现对伺服电机的控制。通过以上闭环控制,悬浮物则可达到稳定悬浮的状态。

图9 单自由度磁悬浮控制系统工作原理Fig.9 Single degree freedom magnetic suspension control system working principle diagram
5.2 位移跟踪试验
采用与仿真分析相同的初始条件,对悬浮物偏离平衡位置的位移z(与仿真不同,试验中采用位移传感器实际测量值)、盘状永磁铁的旋转角度θ、电机输入电流i进行跟踪,结果如图10所示。试验系统的响应结果与仿真分析基本一致;由于系统数学模型的不够精确,所得的控制器在实际控制过程中,悬浮物的位移、角度和电机输入电流i在响应过程中产生了超调量。稳态时的位移、角度、电流均在平衡位置附近小幅震荡。
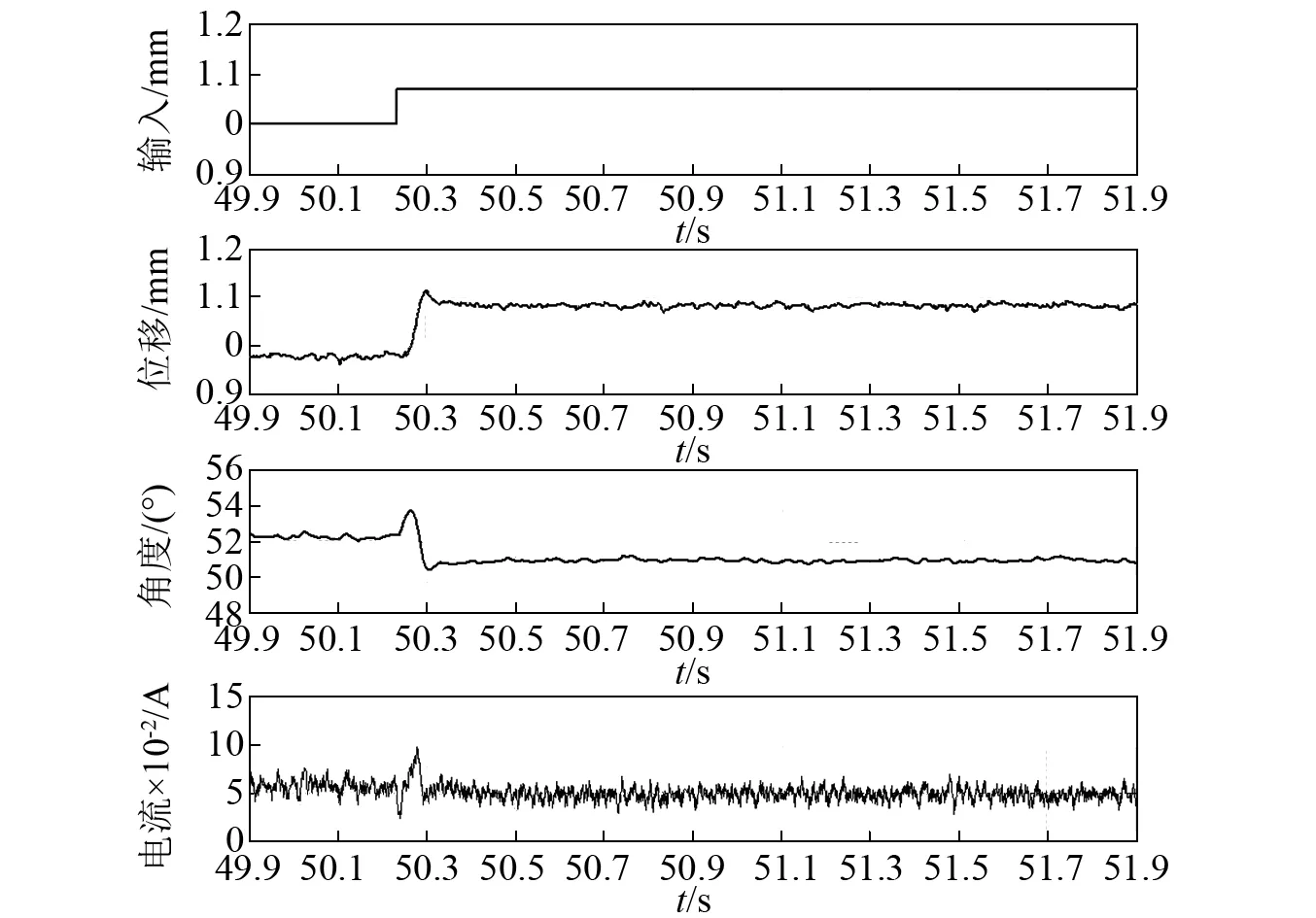
图10 系统对阶跃信号的跟踪实验结果Fig.10 The experiment result of system with step signal
试验结果表明该控制器可以保证闭环系统稳定且快速的跟踪位移输入信号,超调量为15%;当系统参数变化时,系统具有一定的鲁棒稳定性。此外,系统处于稳定状态时,悬浮物的位置在1.086~1.094 mm,位置误差在±0.005 mm左右,系统没有较大的波动现象,稳定性较好。伺服电机的输入电流i基本不变(平衡位置时,电流很小),保持在0.04~0.06 A,系统的总功耗基本保持在很低的水平。
5.3 外扰试验
采用与仿真分析相同的初始条件,在0.4 s时,将质量为3 g的物体从2 cm高处对悬浮物进行冲击试验,并对悬浮物的位移z(与仿真不同,试验中采用位移传感器实际测量值)、盘状永磁铁的旋转角度θ、电机输入电流i进行跟踪,结果如图11所示。试验开始时,悬浮物的位移减小(悬浮气隙增大),在重物从悬浮物上掉落之后时,悬浮物又回到平衡位置,位移幅值的最大变化量为0.05 mm;角度θ先迅速增大,然后又回到平衡位置,角度幅值的最大变化量为1.8°;电流i的变化过程和角度θ的变化过程基本一致,其幅值的最大变化量为0.05 A。
试验结果表明当有外力冲击扰动时,该可以使闭环系统保持稳定,系统可以抑制外部扰动。
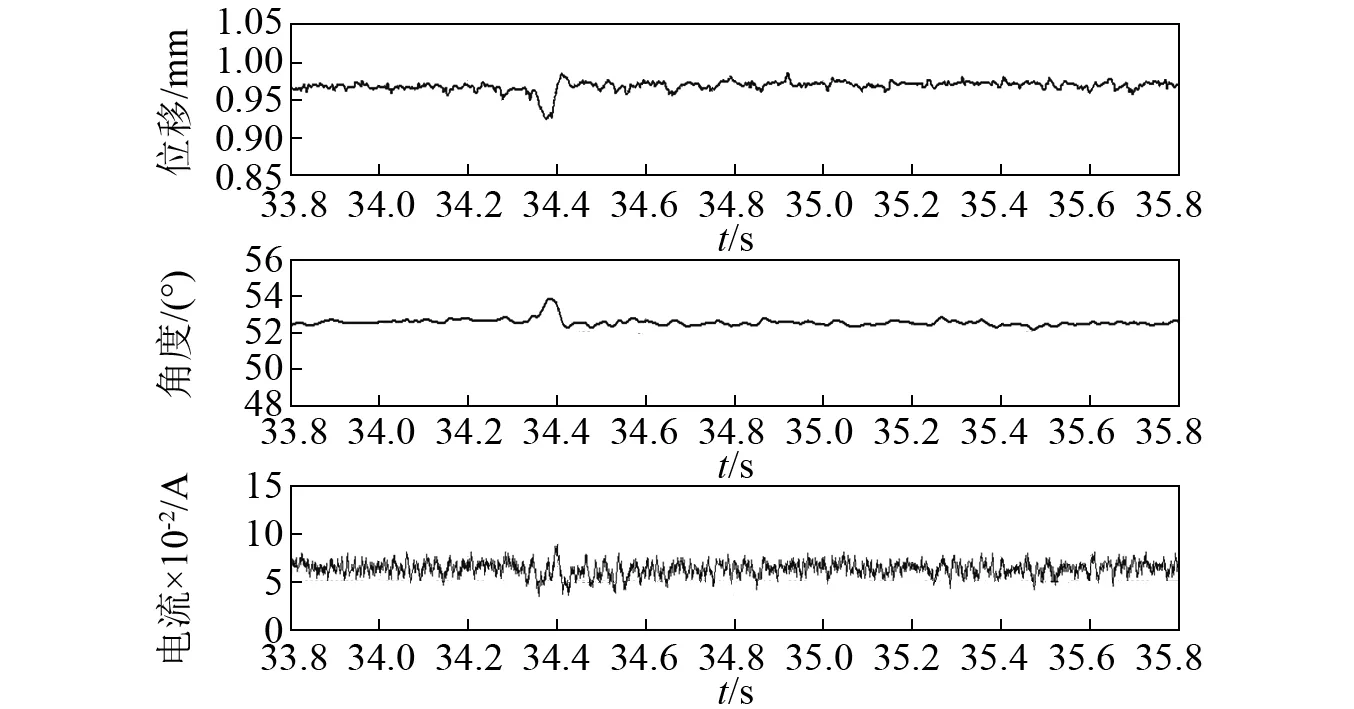
图11 系统受外力扰动的实验结果Fig.11 The experiment result of system with disturbance force
6 结 论
设计了一种可以实现低功耗运行的可控磁路式永磁悬浮系统,并基于有限元软件分析了该系统的可行性,得到了系统力学模型,并针对该可控磁路式永磁悬浮系统的非线性、强耦合,设计了满足系统性能要求的状态反馈γ-次优H∞鲁棒控制器。仿真和试验的结果表明,该控制器可以使闭环系统保持稳定,对参考信号做出快速响应,对系统内部参数不确定引起的扰动以及直接外力扰动具有很强的抑制能力,系统的鲁棒性较好。控制器满足可控磁路式永磁悬浮系统的性能要求。

