基于深度学习特征提取和WOA-SVM状态识别的轴承故障诊断

赵春华,胡恒星,陈保家,张毅娜,肖嘉伟

(1.三峡大学 水电机械设备设计与维护湖北省重点实验室,湖北 宜昌 443002；2.三峡大学 机械与动力学院,湖北 宜昌 443002)

滚动轴承作为旋转机械的重要组成部分，在现代工业生产中占据着重要地位。对滚动轴承进行实时准确的状态监测和故障诊断，不仅能够保证旋转机械的性能和稳定性，而且还能延长机械的使用寿命。传统故障诊断可归纳为特征提取和状态分类两个步骤。传统特征提取方法需要依赖大量信号处理技术和人为主观判断，其中包括频域统计分析、倒频谱分析、小波变换和经验模式分解等[1-2]；而状态分类可由K-近邻算法、SVM(Support Vector Machine)、朴素贝叶斯等[3-6]机器学习算法来实现，这些机器学习方法大多数都是监督学习，需要大量的数据标签，而在实际监测环境中获得的数据大部分是无标签数据，这就给轴承的故障诊断带来了复杂性，同时传统机器学习模型分类面临维数灾难、过拟合等问题，其浅层模型难以表征信号样本与健康状况之间复杂的映射关系，且缺少必要的泛化能力[7-8]。

近年来，由于神经网络可以通过隐含层自适应提取到数据的高维特征，所以已经广泛应用到机械故障诊断领域。同时，2006年Hinton等[9]通过逐层贪婪训练法解决了深度神经网络难训练、易陷入局部最优解的问题，使得深度学习得到迅速的发展。李巍华等[10]利用深度信念网络对轴承振动原始信号进行处理，取得了较高的轴承故障分类识别率，避免了特征提取与选择的复杂性，增强了识别过程的智能性。朱煜奇等[11]通过栈式降噪自编码网络成功的挖掘高维深层的轴承故障特征，验证了该方法对故障的识别能力和泛化能力。温江涛等[12]利用变换域的压缩采集和堆叠稀疏自编码网络对轴承故障信号进行自适应特征提取及诊断，实现了智能、准确的分类。这些非监督式的深度神经网络可以摆脱对大量标签的依赖，同时降低特征提取的复杂性，提高了分类准确率。

针对上述问题，本文提出一种深度学习自适应提取故障频域特征和时域统计特征相融合，并通过WOA-SVM(Whale Optimization Algorithm-SVM)进行状态识别的模型。该模型优势在于：①通过建立深度网络模型，利用逐层贪婪编码的方法实现低维简单特征到高维复杂特征的数据挖掘过程，摆脱了人为提取样本特征的复杂过程，实现了轴承故障诊断的智能化；②深度学习提取故障频域特征与人工提取时域特征相融合，提高了故障诊断的准确率和可靠性；③通过实验台数据分析对比GA-SVM和PSO-SVM模型识别方法，结果表明，WOA-SVM具有更高的状态识别率以及更快的计算速度。

1 基于深度学习的特征提取

Hinton等提出的深度学习理论用于构建深度神经网络(Deep Neural Network，DNN)，可以通过组合低层特征形成更加抽象的高层特征表示，从而发现数据的分布式特征表达，与浅层神经网络相比，深度神经网络具有更加优异的表达能力。针对加速度传感器采集到的机械故障信号，本文提出基于堆叠降噪自编码方法实现对故障信号的自适应提取。该方法通过非监督式贪婪训练法达到逐层初始化的目的，以解决深度神经网络难以训练的问题，再利用监督式BP算法进行微调，使DNN具有特征学习能力和判别能力。

1.1 基本自编码网络

基本自编码器是三层的非监督神经网络，分为编码网络与解码网络两个部分，如图1所示。自编码器的输入层和输出层维数相同，自编码器的本质是学习一个相等函数，即网络的输入和重构后的输出相等，故编码矢量成为了输入数据的一种特征表示，即实现非线性特征降维，这种相等函数的表示缺点是当测试样本和训练样本相差较大，即不符合同一分布时，效果不好，而降噪自编码器在这方面的处理有所进步[13]。

1.2 降噪自编码网络

降噪自编码器(Denoising Autoencoder，DAE)结构如图2所示。编码网络将以一定概率将输入层节点的值置为0，从而得到含有噪声的样本数据，然后对样本进行编码；解码网络再根据受到噪声干扰的数据中估计出未受噪声干扰样本的原始形式，从而使DAE从含噪样本中学习到更具鲁棒性的特征，降低DAE对微小随机扰动的敏感性。DAE的原理与人的感知机理类似，比如人眼看物体时，如果物体某一小部分被遮住了，人依然能够将其识别出来；另外，多模态信息输入人体时(比如声音，图像等)，少了其中某些模态的信息有时影响不大[14]。因此降噪自编码器可有效减少机械工况变化与环境噪声等随机因素对提取的状况信息的影响，使特征表达的更具有鲁棒性[15]。

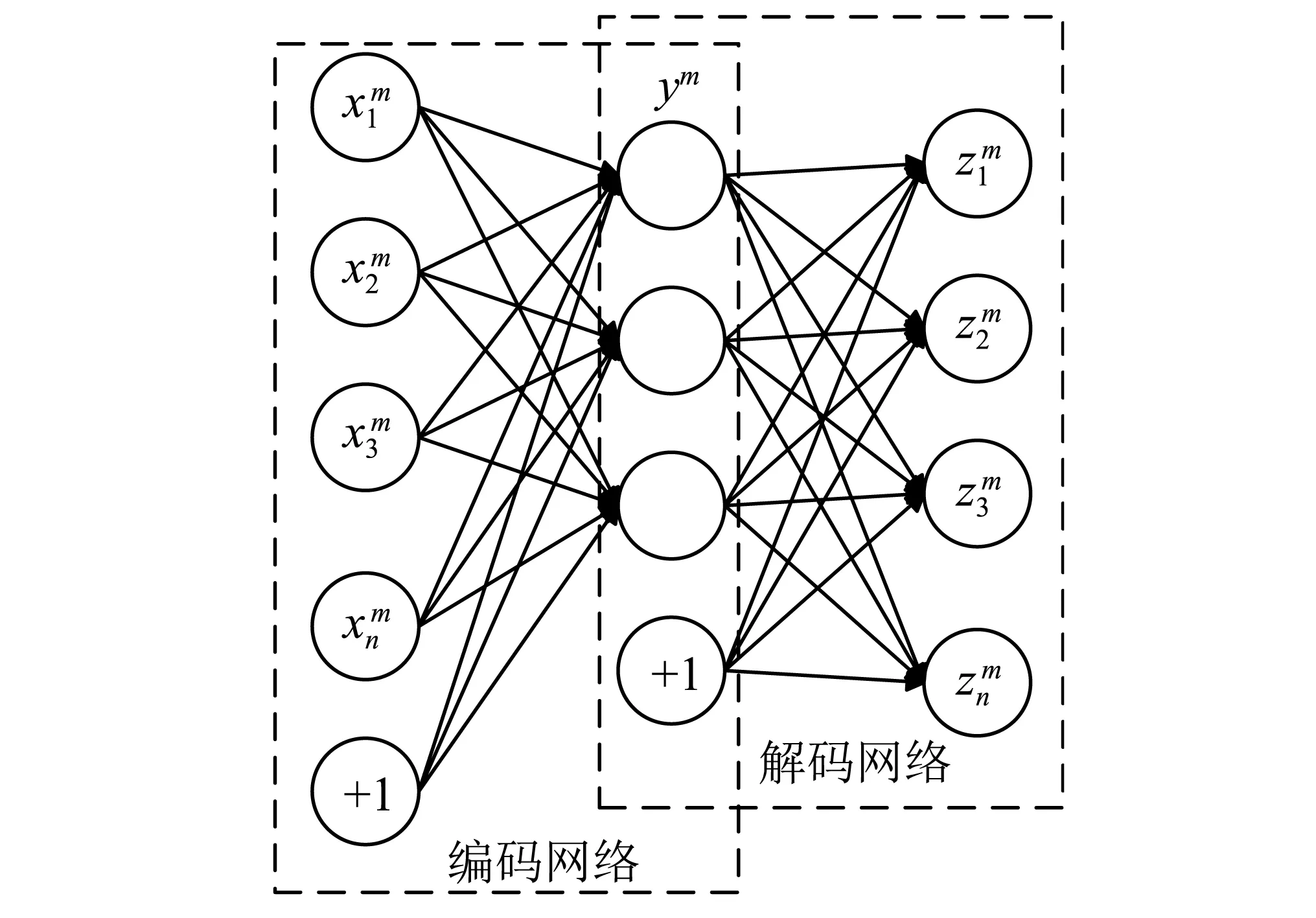
图1 基本自编码网络Fig.1 Basic auto-encoder network

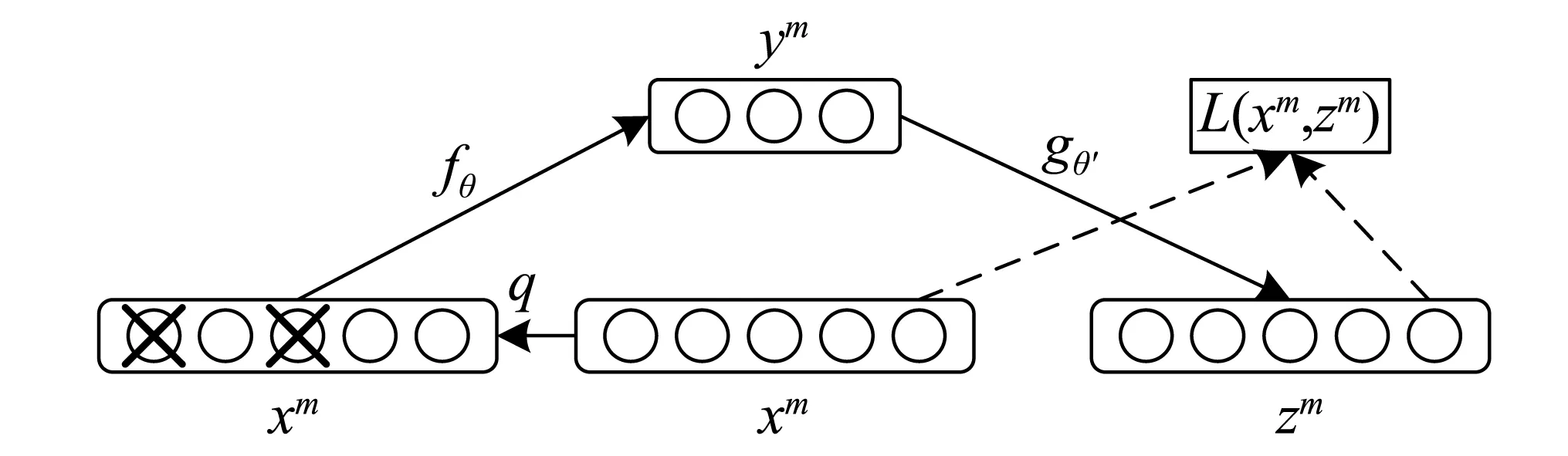
图2 降噪自动编码器原理图Fig.2 Schematic diagram of denoising auto-encoder

假设降噪自编码网络的输入层为{x1,…,xm,…,xM},式中上标表示第m个样本，总共有M个训练样本。输出层为{z1,…,zm,…,zM}。网络结构的损失函数为

(1)

编码网络阶段，输入信号为前一个自编码结构的编码层的值(第一层网络结构的输入层为原始输入信号。其数学表达式为

(2)

解码网络阶段，将重构出没有添加噪声前的原始输入信号，其数学表达式为

zm=gθ′(ym)=sg(W′ym+d)

(3)

式中：ym为编码层输出值；sg为解码网络的响应函数；θ′为解码网络的参数集合，且θ′={W′,d}；W′,d分别为解码网络的连接权值和偏置参数。

由上述过程可知，降噪自编码器属于非监督学习，不需要任何标签，依靠最小化输出层与输入层信号间的重构误差，得到编码层的降维特征。

为了防止结构过拟合增强特征的聚类能力和判别能力，在降噪自编码器的损失函数中加入稀疏性惩罚项，即得到稀疏降噪自编码器，其损失函数数学表达式为

(4)

式中：λ为惩罚因子，控制网络的稀疏程度。

稀疏自编码网络有着天然的聚类性质，能够充分发挥数据所含有的信息，去掉冗余的数据信息，最大化利用数据，使得高层网络层能够表达原始数据本质特征，并且具有很强的判别能力。

1.3 堆叠降噪自编码器预训练与微调

降噪自编码器的浅层网络结构函数表达能力有限。为了增强网络的表达能力，多个DAE依次堆叠构成深度网络结构，即堆叠降噪自编码器(Stacked Denoising Autoencoder，SDAE)[16]，如图3所示。由于DAE各层满足归一化要求，因此将上一个DAE的编码层作为下一个DAE的输入，以此类推，通过逐层贪婪训练得到自适应非监督提取的特征，但是逐层最优并不能确保堆叠后分类器整体最优。为了确保堆叠后整体最优，此时需要带有标签的样本数据，采用BP算法进行监督式训练，实现微调。对每一层预先分别训练，可以避免传统深度结构容易陷入局部极小值的问题[17]。相较于传统的神经网络随机初始化权重，深度学习网络的初始参数是通过无监督学习得到，更接近于全局最优值。

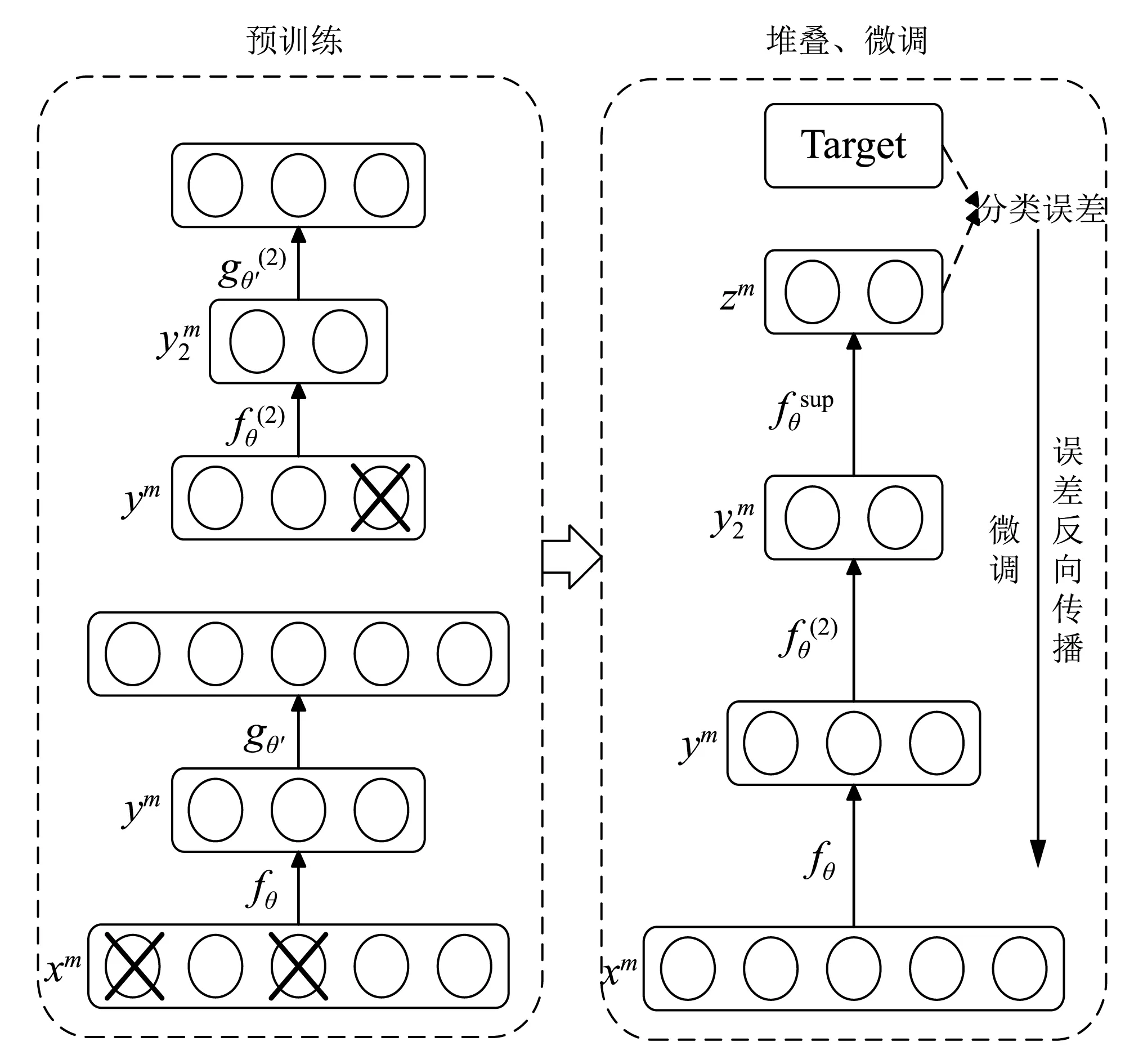
图3 堆叠降噪自编码器预训练与微调示意图Fig.3 Pre-training and fine-tuning of the stacked denoising auto-encoder

2 WOA-SVM原理

2.1 WOA算法介绍

Mirjalili等[18]于2016年提出了鲸鱼优化算法(WOA)，该算法对鲸鱼的“螺旋气泡网”策略、收缩包围、螺旋式位置更新和随机捕猎机制不断逼近猎物的狩猎过程进行数学模拟，其具有调节参数少、全局收敛性强、收敛速度快等特点。WOA数学模型包括环绕式包围捕食、泡泡网攻击猎物和随机搜索捕食3个阶段。

2.1.1 环绕式包围捕食

座头鲸在寻找猎物时，能够识别它们的位置并将其包围。具体数学模型为

D=|CX*-X(t)|

(5)

X(t+1)=X*(t)-AgD

(6)

式中:t为当前迭代次数；X*为当前获得的猎物位置向量；X为鲸鱼位置向量；A和C为系数向量，其定义为

A=2agr-a

(7)

C=2gr

(8)

式中:a为收敛因子，随迭代次数增加从2线性减小到0，表达式为a=2-2t/M，其中M为最大迭代次数；r为[0，1]之间的随机向量。

2.1.2 泡泡网攻击猎物

为了建立鲸鱼的泡泡网攻击行为的数学模型，设计了两种方法来模拟这种行为，数学模型如下：

(1)收缩包围圈机制(Shrinking Encircling Mechanism,SEM),实现该行为只需要减少式(8)中的a，需要注意的是A随着a的减小而缩小。

(2)螺旋式位置更新(Spiral Updating Position,SUP),座头鲸以螺旋运动方式不断接近猎物，其螺旋运动的数学模型为

X(t+1)=D′geblgcos(2πl)+X*(t)

(9)

式中:D′=|X*(t)-X(t)|为第i条鲸鱼和猎物的距离；b用于定义螺旋形状的常数；l为[-1，1]的随机数。

但要注意，鲸鱼沿着螺旋形状运动时，同时在收缩包围圈，为了模拟这种同步行为，Mirjalili等假设选择收缩包围圈机制或螺旋位置更新概率均为50%。数学模型为

(10)

式中:p为[0，1]上的随机数。

2.1.3 随机搜索捕食

座头鲸可以随机更新个体位置捕食猎物。鲸鱼根据相互之间的位置进行随机搜索，具体过程为

D=|CgXrand-X|

(11)

X(t+1)=Xrand-AgD

(12)

式中:Xrand为从当前群体中随机选择的个体位置向量。

2.2 WOA-SVM参数优化

WOA-SVM寻优过程为：首先，在搜索空间中随机产生N个鲸鱼个体组成初始种群；接着在进化过程中，群体根据当前最优鲸鱼个体或随机选取一个鲸鱼个体更新各自的位置；然后，根据随机产生的数p决定鲸鱼个体进行螺旋或包围运动；最后，循环迭代至WOA算法满足终止条件。流程图如图4所示。通过WOA对SVM进行参数寻优，可以避免传统人工反复试错的过程，结合WOA算法的调节参数少、结构简单、收敛速度快等特点，实现对SVM的惩罚因子c和核参数g的快速寻优，来提高WOA-SVM状态识别的正确率。试验中，以交叉验证意义下支持向量机的平均分类准确率作为适应度函数，评价鲸群中每个个体的适应度，适应度较高的成员被保留，试图找到搜索空间内的最佳适应度所对应的c和g。同时，针对惩罚因子c过大会导致过拟合现象的发生，也会使分类器的泛化能力降低，对WOA-SVM作出改进

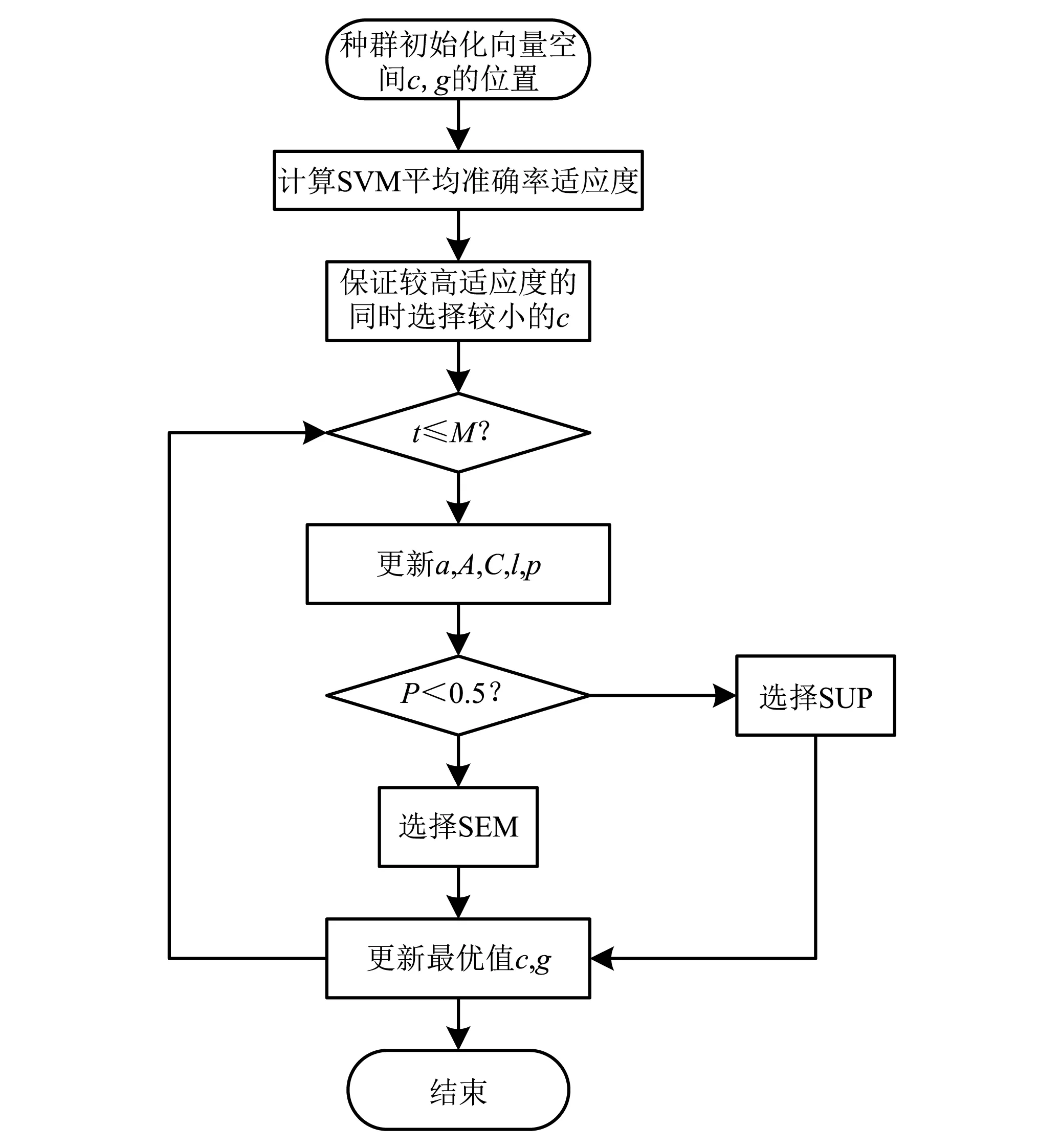
图4 WOA-SVM算法流程图Fig.4 WOA-SVM algorithm flow chart

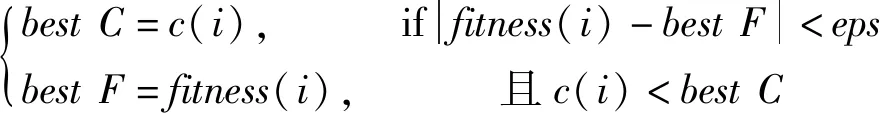
(13)

式中：bestC为当前鲸群最佳惩罚因子c；bestF为当前鲸群最佳适应度；c(i)和fitness(i)分别为第i个鲸鱼的惩罚因子c与适应度；eps=0.1为允许降低适应度的阀值；这样就可以在保证得到较高的适应度时，获得较小的惩罚因子c。

3 基于深度学习特征提取和WOA-SVM状态识别的轴承故障诊断

3.1 模 型

基于深度学习特征提取和WOA-SVM状态识别分类模型可以实现设备故障诊断，如图5所示。振动信号一般作为轴承故障的分析对象，可以选择时域分析，也可以选择频域分析，试验表明，频域信号更加适合作为分类器输入。相较于传统机器学习，堆叠稀疏降噪自编码网络可以处理高维特征，最大限度保留了样本信息，通过多个稀疏降噪自编码叠加，可以有效的提取到输入样本的高维特征，再将高维特征输入WOA-SVM实现轴承的故障诊断。综上，构建以轴承振动信号频谱序列为输入，堆叠稀疏降噪自动编码器提取高维特征，以WOA-SVM作为故障分类器，可以实现基于深度学习特征提取和WOA-SVM状态识别的轴承故障诊断。

图5 基于深度学习特征提取和WOA-SVM状态识别分类模型Fig.5 Classification model based on deep learning feature extraction and WOA-SVM state recognition

3.2 试验与验证

为了验证深度学习神经网路在故障特征提取中的效果，在自制滚动轴承试验台上进行故障模拟试验，试验装置如图6所示，本试验台可以模拟滚动轴承多种故障，如裂纹、腐蚀、剥落等。

图6 滚动轴承系统试验台Fig.6 Rolling bearing system test bench

利用该试验台模拟了滚动轴承的10种健康状况，如表1所示。试验分3种不同转速(500 r/min，800 r/min和1 200 r/min)与两种不同载荷(无载荷与加载)下进行。试验中，采样频率20 480 Hz,采样时间持续16 s，根据最低转速500 r/min，轴承转动一圈，传感器约采集2 457个数据点，选取样本长度为2 400作为一个样本。综上，队原始振动信号随机不重叠可以采集大约7 440个样本，每一种故障状态的样本个数均为744，即每种故障状态在单一工况下有124个样本，考虑到算法优化时间成本，只随机选取3 720个样本集，其中3 300个样本作为训练集，剩余的420个样本作为测试集。

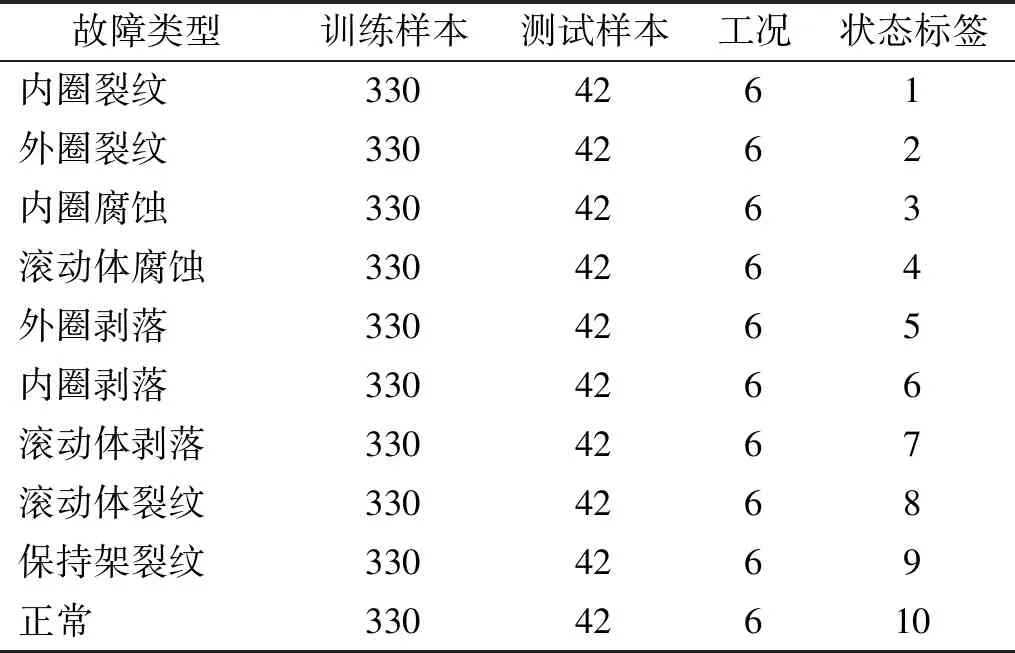
表1 滚动轴承试验的10种健康状况Tab.1 10 health conditions of the rolling bearing experiment

将采集到的样本经过快速傅里叶变换为频谱序列并归一化，以1 200维的频谱序列作为输入堆叠降噪自编码网络。本文中DNN设置为5层，网络结构为1 200-450-150-50-10，神经元激活函数为sigmoid函数，输入样本去噪率为0.5，输入层神经元个数由样本长度决定，输出层由标签类别决定。预训练和微调阶段，将模型迭代次数设定为50。将经微调后得到的降维数据输入WOA-SVM中进行分类。其中：采用径向基核函数和5折交叉验证，并以交叉验证意义下支持向量机分类正确率作为适应度函数。WOA算法参数设置和待优化参数范围如表2所示。

3.3 结果分析

为了验证深度学习神经网络能够自适应提取频谱中的有效故障特征，试验中人工提取了14个常用的时域统计特征[19]输入WOA-SVM，与深度学习神经网络自适应提取的故障频谱特征做对比。寻优参数最优值和交叉验证下平均分类正确率和测试集正确率的结果如表3所示，得到的适应度曲线如图7、图8所示。

表2 WOA参数设置和待优化参数范围Tab.2 WOA parameter setting and range of parameters to be optimized

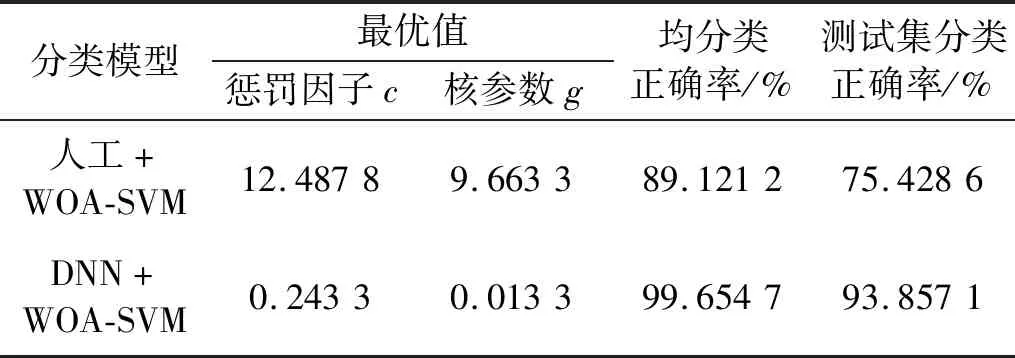
表3 寻优参数最优值及分类正确率Tab.3 The optimal value and classification accuracy of the optimized parameters

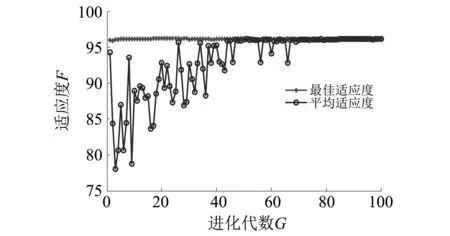
图7 WOA-SVM对人工提取的时域统计特征分类的适应度曲线Fig.7 Fitness curves of time domain statistical feature classification based on WOA-SVM

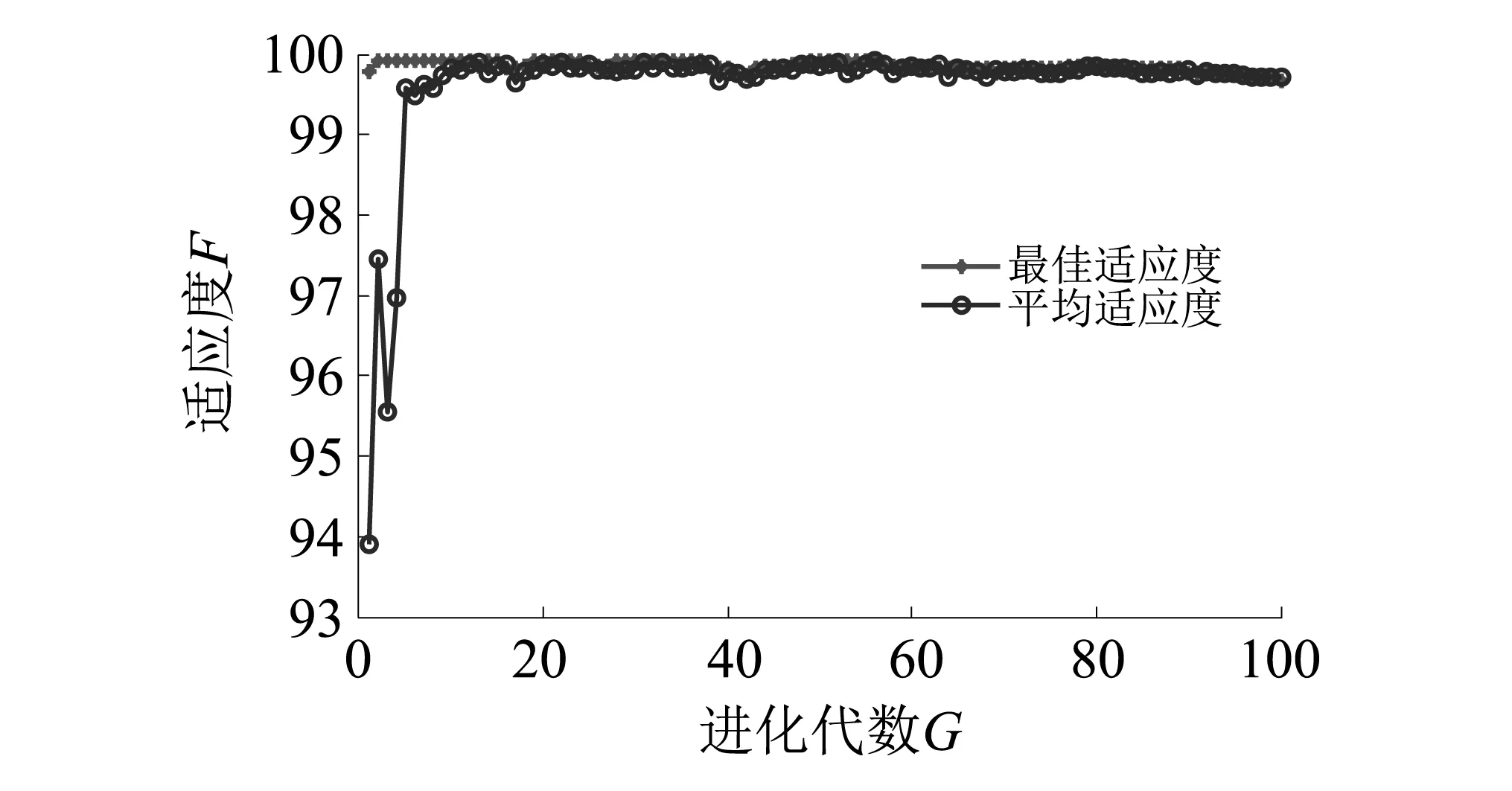
图8 WOA-SVM对深度神经网络自适应提取频域特征的分类适应度曲线Fig.8 Fitness curves of the classification of frequency domain feature which is selected by the DNN based on WOA-SVM

由表3可知，深度学习神经网络自适应提取特征，其测试集在WOA-SVM上分类正确率为93.857 1%。说明深度学习神经网络能够有效的提取故障特征。但人工方法提取的频域状态特征，其测试集在WOA-SVM上分类正确率只有75.428 6%，分析原因，可能是特征表达性不强，惩罚因子c过大，模型训练存在过拟合现象，导致测试集上分类正确率有所下降。

将提取特征的表达性对诊断效果的影响进行深入的分析。对样本进行聚类并投影到贡献率前三的特征向量三维空间中，可以直观的了解特征对样本的表达能力。如图9、图10所示。可知人工方法对样本特征的提取，其中同类样本能实现一定程度的聚集，但不同故障类型下的样本重叠部分较多。相比之下深度学习神经网络自适应提取的故障频谱特征，能够明显地区分不同故障模式下的样本，分类效果更好。

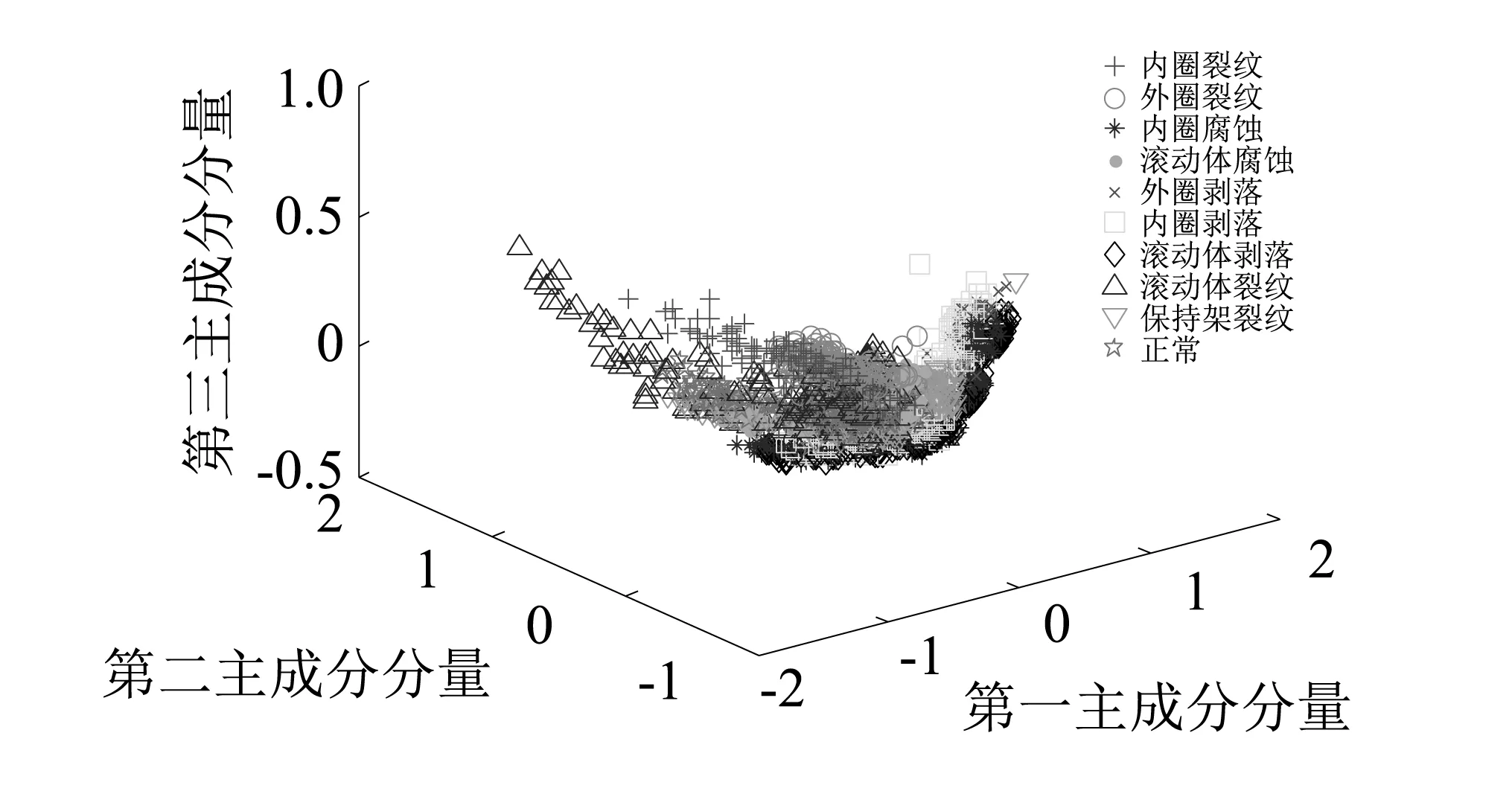
图9 人工方法提取的时域统计特征的主成分散点图Fig.9 Main scatter points diagram of the time domain statistical features extracted by the artificial method

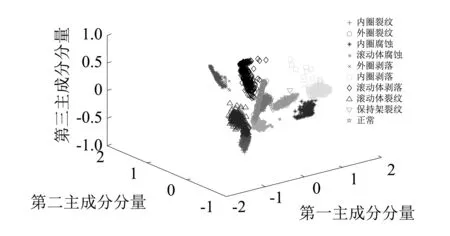
图10 深度神经网络自适应提取的频域特征的主成分散点图Fig.10 Main scatter points diagram of frequency domain feature extracted by the DNN

以上结果表明，深度学习神经网络能够有效提取表达性强的故障特征，摆脱了人工提取频域特征过程的复杂性，实现了诊断过程的智能化，并一定程度上提高了故障分类的正确率。而人工提取特征从高维特征向低维空间投影的过程中损失了大量有用的特征信息，导致某些相似状态下可分性差，影响诊断结果。

4 方法对比

为了验证增加人工提取故障时域特征能够提高WOA-SVM分类器的诊断正确率的可行性和有效性，将文中人工提取的故障时域特征与深度学习提取故障频域特征相结合成的联合特征输入WOA-SVM分类器中，并与SDAE和深度置信网络(Deep Belief Network，DBN)诊断能力作比较，试验重复进行10次以减少随机扰动，对比结果如图11所示。可以看出，提出方法的平均诊断准确率为96.64%要高于直接用SDAE诊断的平均诊断准确率90.89%和DBN的平均诊断准确率81.71%,证明增加时域统计特征后，能提高分类器对故障的分类准确率。

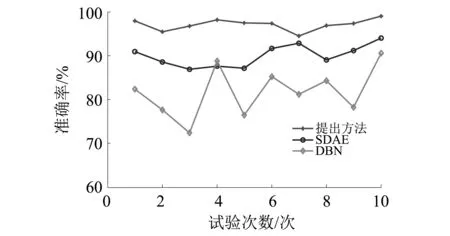
图11 10次试验中的诊断准确率Fig.11 Diagnostic accuracy in the 10 tests

为了验证WOA-SVM具有更快的收敛速度，和更高的准确率，将其与GA-SVM和PSO-SVM作比较，把深度学习神经网络自适应提取的故障特征分别输入WOA-SVM,GA-SVM和PSO-SVM中进行故障分类。WOA算法参数设置同表2所示，GA和PSO算法基本参数和待优化参数范围如表4所示。得到的适应度曲线如图12、图13所示。

由表5可知，在交叉验证下的平均分类正确率3种算法均能达到99.9%以上，而在测试集上WOA-SVM方法分类正确率略高于GA-SVM和PSO-SVM，并且WOA-SVM的寻优时间明显快于GA-SVM和PSO-SVM。

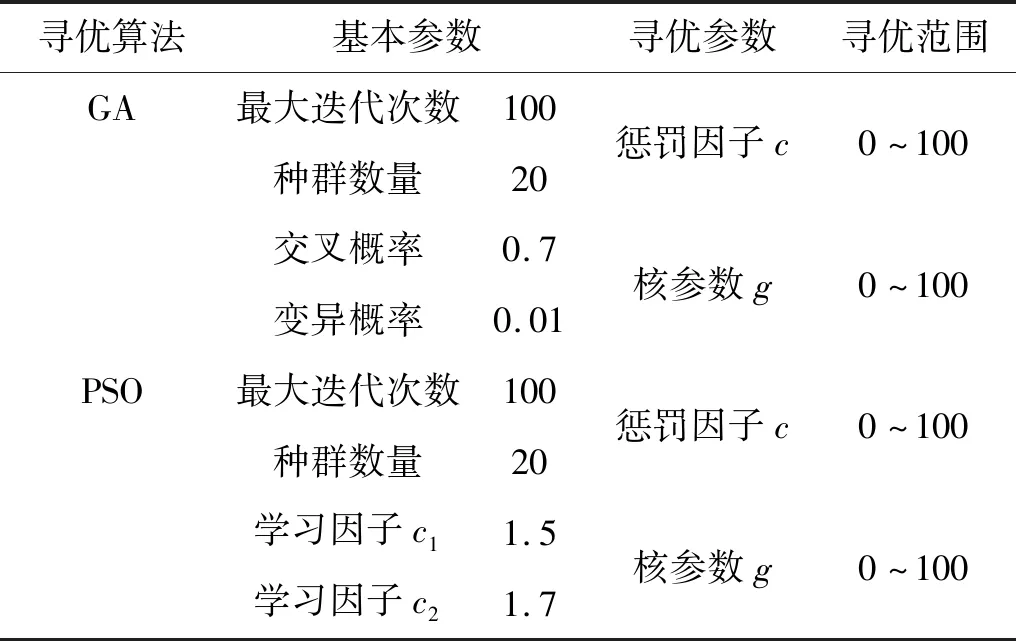
表4 GA和PSO基本参数设置和待优化参数范围Tab.4 Basic parameter settings of GA and PSO and the range of parameters to be optimized

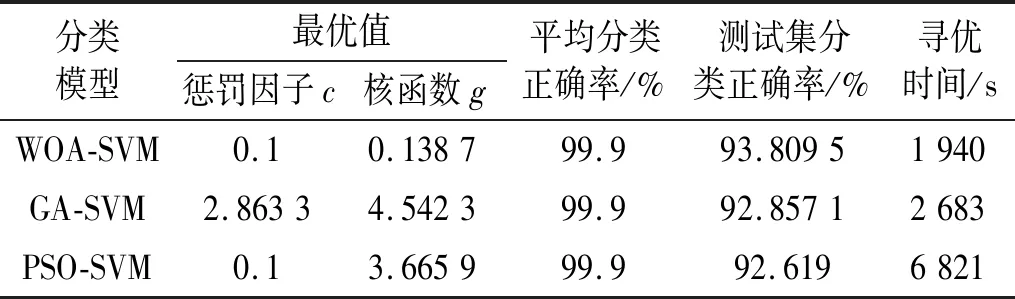
表5 3种优化算法结果对照表Tab.5 Comparison table of results of three optimization algorithms

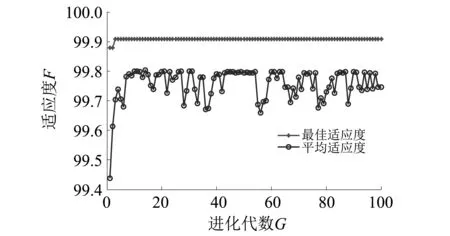
图12 GA-SVM对深度神经网络自适应提取频域特征的分类适应度曲线Fig.12 Fitness curves of the classification of frequency domain feature which is selected by the DNN based on GA-SVM

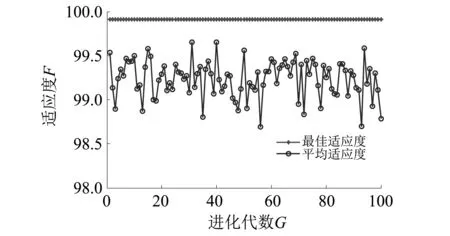
图13 PSO-SVM对深度神经网络自适应提取频域特征的分类适应度曲线Fig.13 Fitness curves of the classification of frequency domain feature which is selected by the DNN based on PSO-SVM

5 结 论

(1)提出了一种基于深度学习特征提取和WOA-SVM状态识别的故障诊断方法，通过DNN网络对原始数据进行非线性降维能获得有效的频谱特征，摆脱了对大量信号处理知识和诊断工程经验的依赖。用WOA-SVM做故障分类器取得较高的故障诊断精度。

(2)比较直接通过SDAE与DBN进行故障诊断的方法，提出的方法在滚动轴承故障诊断上取得较高正确率，证明了该方法的有效性。

(3)WOA算法具有调节参数少，收敛速度快，寻优精度高等优点，WOA-SVM较GA-SVM与PSO-SVM节省了大量优化时间，并在一定程度上提高了故障分类正确率。