基于双横臂的1/4汽车模型及其等效模型的建模控制研究

朱柏霖，秦 武，上官文斌，Subhash Rakheja

(华南理工大学 机械与汽车工程学院，广州 510641)

悬架系统作为所有车辆的重要组成部分，其主要作用是承受车身重量，衰减来自路面的不平度激励和提供良好的轮胎路面接触以确保车辆的行驶安全性[1]。半主动悬架系统的控制力由CDC(Continuous Damping Control)减振器或磁流变减振器产生，控制算法一般采用不依赖系统参数的天棚控制算法[2]。目前研究论文中，虽然提出了很多类似于天棚控制的半主动控制算法，例如SH-ADD(Mixed Sky-Hook and Acceleration-Driven-Damper)[3]、SH-PDD(Mixed Skyhook and Power-Driven-Damper)[4]等，但是由于需要复杂的信号输入和准确模型参数等原因，上述算法还没有运用到实车上。半主动悬架相比于主动悬架，具有更好的稳定性，但控制效果相对较差[5]。

在悬架的主动控制研究方面，目前有各种基于各种控制理论的主动悬架控制算法。较为成熟的算法有线性二次最优控制算法LQG(Linear Quadratic Gaussian Control)[6]和滑模控制算法[7]等，这些算法都需要知道准确的悬架模型参数。控制算法中需要的一些状态变量一般通过状态观测器获得，而构造状态观测器也需要获取悬架模型的准确参数[8-9]。基于以上原因，基于主动算法的主动悬架，目前在实车上应用较少。

在悬架的主动控制算法的研究中，控制算法和状态观测器都是在简单的二自由度模型的基础上推导和证明的。研究表明，使用名义参数的二自由度模型能够很好地反映麦弗逊悬架的振动特性[10]。但是对于结构更复杂的双横臂悬架，使用名义参数的二自由度模型求得的簧载质量和非簧载质量的响应与由基于双横臂悬架的1/4汽车模型求得的响应相差较大[11]。如果使用辨识参数的二自由度模型能够真实体现双横臂悬架的振动特性，将加强这些依赖悬架模型参数的控制算法的实用性。因此，在进行双横臂悬架控制算法设计时，需要通过参数辨识方法得到准确的二自由度模型参数。

目前在基于悬架三维多体动力学的1/4汽车模型计算得到的簧载质量和非簧载质量的响应，来识别简化二自由度模型参数的辨识算法中，在三维多体动力学建模时，没有考虑悬架中橡胶弹性元件(如悬架摆臂衬套、减振器上端支撑等)的影响，并且都把减振器设置为线性阻尼特性[12-13]。

综上所述，目前半主动悬架和主动悬架的研究主要集中在控制算法上，对控制算法在实际应用中的有效性研究较少。在辨识1/4汽车模型的等效二自由度模型的参数时，对等效为真实1/4汽车系统的仿真模型作了过多的简化。

本文首先建立了基于双横臂悬架的1/4汽车三维多体动力学模型，模型中将减振器设置为分段线性阻尼特性(拉伸阻尼系数和压缩阻尼系数)。根据1/4汽车模型的簧载质量和非簧载质量的响应，辨识出等效二自由度模型的参数。研究了悬架系统中橡胶弹性元件的刚度特性对等效二自由度模型参数辨识结果的影响。建立了基于参考模型的滑模控制算法，证明了等效二自由度模型的参数辨识对控制算法的重要性和必要性。

1 基于双横臂悬架的1/4汽车模型和等效二自由度模型

图1(a)为基于双横臂悬架的1/4汽车模型(下文简称1/4汽车模型)，图1(b)为等效的二自由度模型。两个模型等效的原则是：利用二自由度模型和利用1/4汽车模型计算得到的簧载质量与非簧载质量的响应接近。首先建立1/4汽车模型，计算其簧载质量和非簧载质量的动力学响应。通过参数辨识的方法，辨识等效二自由度模型的参数，使得由采用辨识参数的等效二自由度模型计算得到的簧载质量和非簧载质量的响应与由1/4汽车模型计算得到的动力学响应一致。

1/4汽车模型由上下控制臂、车轮与转向节、弹簧与减振器，以及转向横拉杆连接而成，如图1(a)所示。上、下控制臂的一端分别通过衬套B1，B2，B3，B4与车身相连，另一端分别通过球铰C和G与转向节相连；车轮与转向节刚性连接，视为一个刚体；弹簧与减振器上端通过橡胶支撑TM与车身相连，下端通过球铰A与下控制臂相连；转向横拉杆一端由球铰F与车身相连，另一端则由球铰E与转向节相连；车身设置为只有垂向自由度的簧载质量块。

1/4汽车模型参数的数值根据附表1进行设定，其中各参数数值为单个元件的物理特性参数的数值，即名义值。橡胶元件的刚度表现为非线性特性，建模时只考虑其在局部坐标系下的线性段刚度，具体参数见附表2[14]。计算分析时，保证输入激励使橡胶元件的变形保持在线性段内。

图1 基于双横臂悬架的1/4汽车模型和等效二自由度模型Fig.1 Diagram of a quarter-car model with double wishbone suspension and an equivalent 2DOFs model

1.1 等效二自由度模型参数辨识方法

本文采用最小二乘法[15]对二自由度模型进行参数辨识，已知参数与需要辨识的参数如表1所示。

表1 已知参数与辨识参数Tab.1 Known and identified parameters

根据图1(b)可以得到二自由度模型在平衡位置的运动微分方程

(1)

式中:fs,fd和ft分别为弹簧力、阻尼力和轮胎动载荷，分别定义为

fs=kszsus=ks(zs-zu)

(2)

(3)

(4)

式中：zsus为悬架相对位移。

令需要辨识的参数向量为

A=[ms,mu,ks,c1,c2]

(5)

状态变量为

(6)

(7)

即可将式(1)所示的微分方程写成矩阵的形式

(8)

(9)

令∂E/∂A=0，将得到

(10)

因此，需要辨识的参数即由式(11)求得

(11)

1.2 等效二自由度模型参数辨识结果

在对1/4汽车模型及其等效二自由度模型进行的动力学响应分析时，路面位移输入为阶跃输入函数，表达式见式(12)，单位为mm，其图形见图2。

(12)

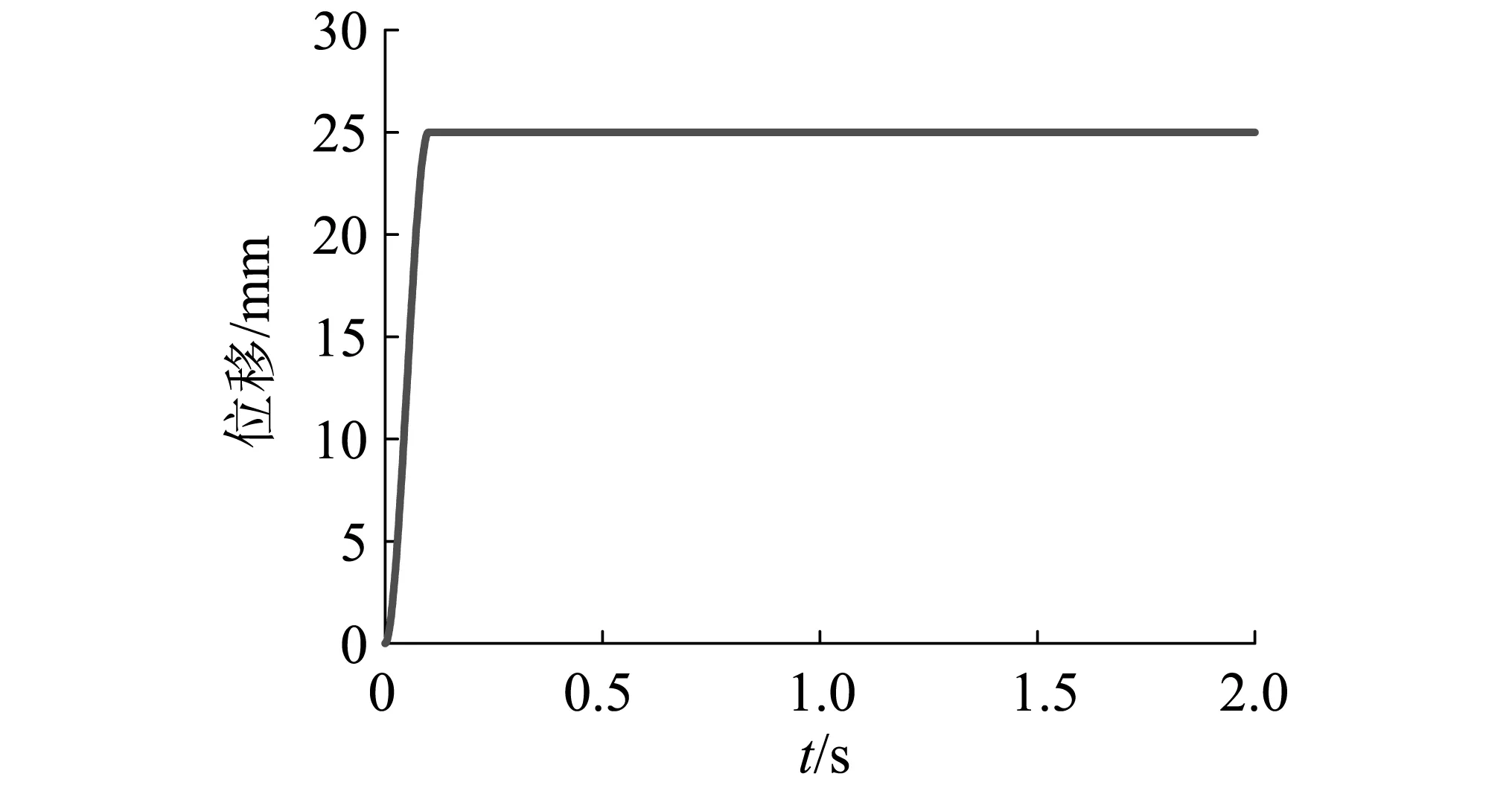
(a)时域

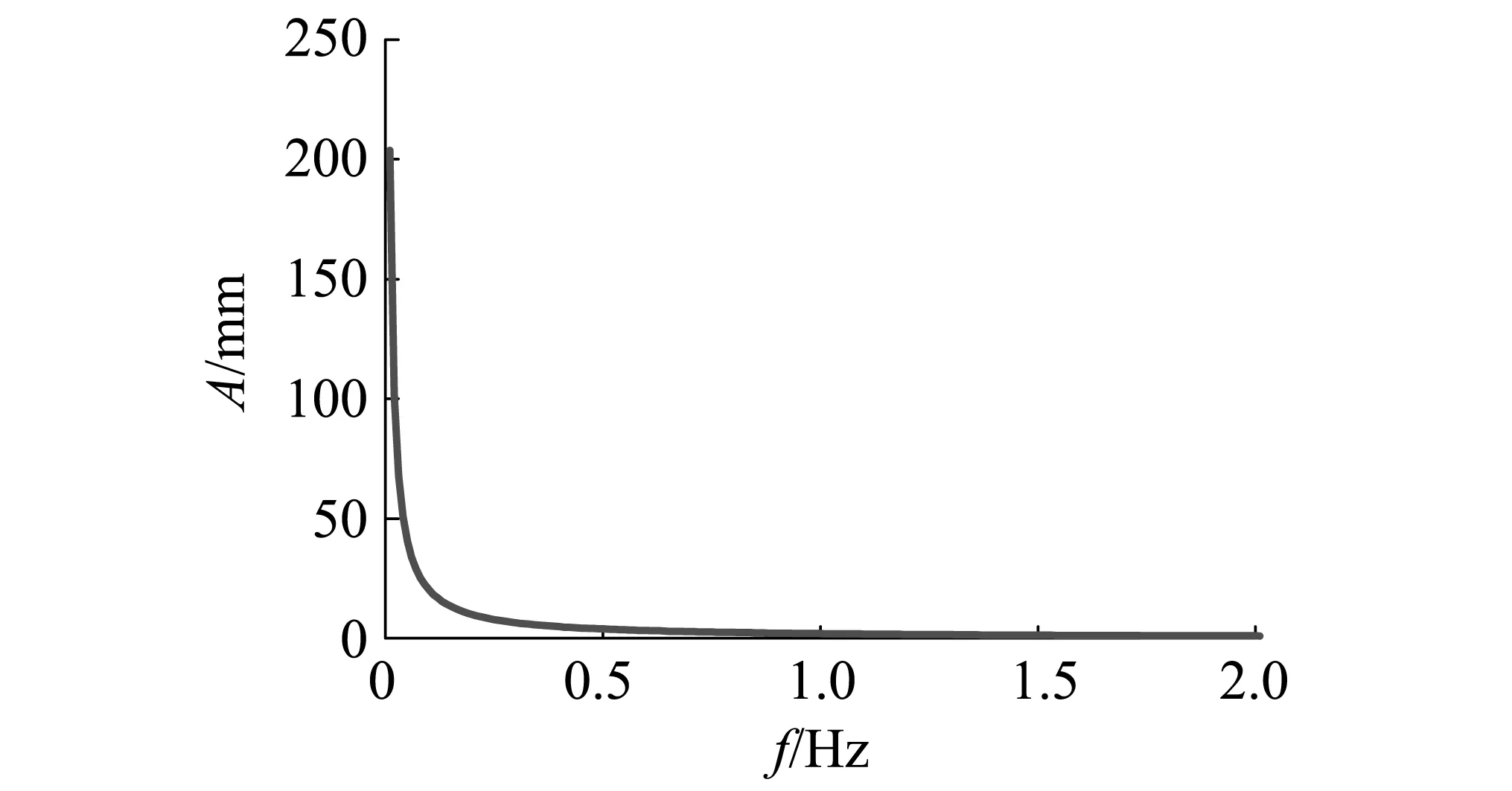
(b)频域图2 路面位移阶跃输入Fig.2 Step input of road displacement

不考虑悬架中橡胶元件的刚度特性，1/4汽车模型的动力学响应的计算值见图3。将位移阶跃输入下得到的1/4汽车模型的动力学响应(见图3)数据代入式(11)，计算得到的等效二自由度模型参数见表2。由表2可知，等效二自由度模型中的刚度和阻尼系数的数值和1/4汽车模型中相关参数的名义值有较大的差异。这是由于悬架结构引起的非线性、悬架减振器阻尼系数的非线性等引起的。相对于名义值，辨识参数中的悬架弹簧刚度和拉伸阻尼系数的数值都减小了56%，而压缩阻尼系数的数值只减小了26%。但是等效二自由度模型中的质量参数的数值与名义值接近，说明由悬架结构、悬架减振器阻尼系数引起的非线性对等效二自由度模型中的质量参数影响较小。

图3 位移阶跃输入下的1/4汽车模型的响应Fig.3 Dynamic responses of a quarter-car model under the step input of displacement

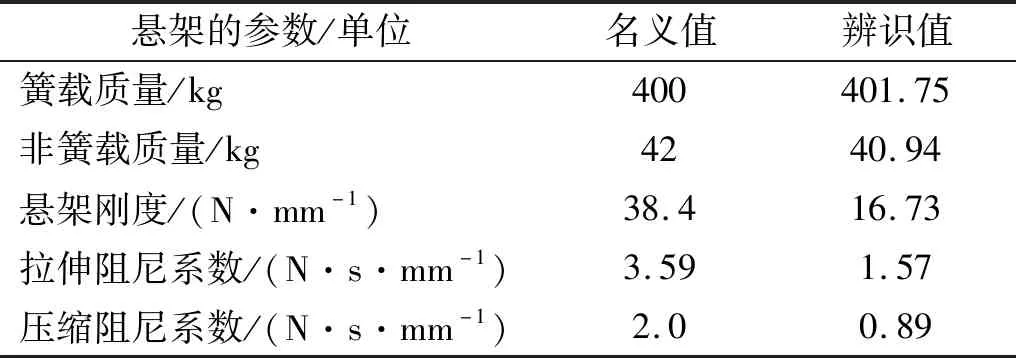
表2 等效二自由度模型参数辨识结果Tab.2 Identified parameters of the equivalent 2DOFs model

1.3 参数辨识结果的验证

为了下文叙述方便，对分析的不同1/4汽车模型和等效二自由度模型进行定义，见表3。将模型Ⅰ～模型Ⅲ的动力学响应特性在时域和频域中进行对比，如图4和图5所示。

表3 1/4汽车模型和等效二自由度模型的定义Tab.3 Definitions of a quarter-car model and an equivalent 2DOFs model

模型Ⅰ～模型Ⅲ的时域响应分别通过ADAMS建模求解和基于Matlab/Simulink软件编程求解。由于这些模型均是具有非线性的模型，其动力学响应的频率响应曲线采用文献[16]中求解非线性系统近似频率响应曲线的方法求得。通过施加单频率正弦位移激励，利用系统响应信号自功率谱与输入信号自功率谱的比值，作为系统响应信号在该频率下的频率响应幅值；不断改变输入正弦位移激励的频率，即可画出一条完整的非线性系统近似频率响应曲线。

由图4可知，模型Ⅰ和模型Ⅱ中簧载质量加速度、非簧载质量加速度、悬架相对位移和轮胎动载荷响应的时域响应曲线几乎重合，证明了辨识方法的准确性；模型Ⅲ的簧载质量加速度和轮胎动载荷的响应曲线幅值比模型Ⅰ的相关量响应幅值大，而模型Ⅲ的非簧载质量加速度和悬架相对位移的响应曲线幅值比模型Ⅰ的相关量响应幅值大小。

由频率响应(见图5)曲线可知，模型Ⅲ中的响应曲线幅值与模型Ⅰ相差较大，并且系统的一阶固有频率也发生了较大变化。因此，使用该最小二乘参数辨识方法得到的等效二自由度模型(模型Ⅱ)比模型Ⅲ更好地表征1/4汽车模型中簧载质量与非簧载质量的运动。

为了研究路面的输入对等效二自由度模型参数辨识结果的影响，采用式(13)的多频率正弦叠加位移输入，单位为mm

图4 模型Ⅰ～模型Ⅲ的时域响应曲线(路面的输入为式(12))Fig.4 Dynamic responses of model Ⅰ—model Ⅲ in time domain (the input of displacement is formula (12))

(a)簧载质量加速度

(b)轮胎动载荷

图5 模型Ⅰ～模型Ⅲ的频率响应曲线
Fig.5 Frequency responses of modeⅠ—model Ⅲ

zr=20sin(2πt)+5sin(2πt×5)+sin(2πt×11)

(13)

在式(13)的输入下，采用上述方法，辨识得到的等效二自由度模型的参数见表4。

由表4可知，多频率正弦叠加位移输入下的辨识结果中的各参数数值与位移阶跃输入下的辨识结果的差异均小于5%，差异较少，证明了所用辨识方法具有通用性。

表4 阶跃和多频率正弦输入下的等效二自由度模型的参数辨识结果对比Tab.4 Identified parameters of the equivalent 2DOFs model under the step and the multi-frequency sine inputs

2 悬架中橡胶元件刚度特性对等效二自由度模型参数辨识结果的影响

悬架中的橡胶元件包括控制臂衬套、减振器上端支撑等橡胶元件，其刚度特性影响汽车的平顺性和操纵稳定性。在1/4汽车模型中，控制臂与车身通过衬套连接、弹簧和减振器与车身通过减振器上端支撑连接。为了下文叙述方便，对建立不同的1/4汽车模型及对应的等效二自由度模型进行定义，见表5。在式(12)的位移阶跃输入下，根据计算四种1/4汽车模型的动态响应，利用第2节中的计算方法，计算得到的等效二自由度模型的参数见表6。

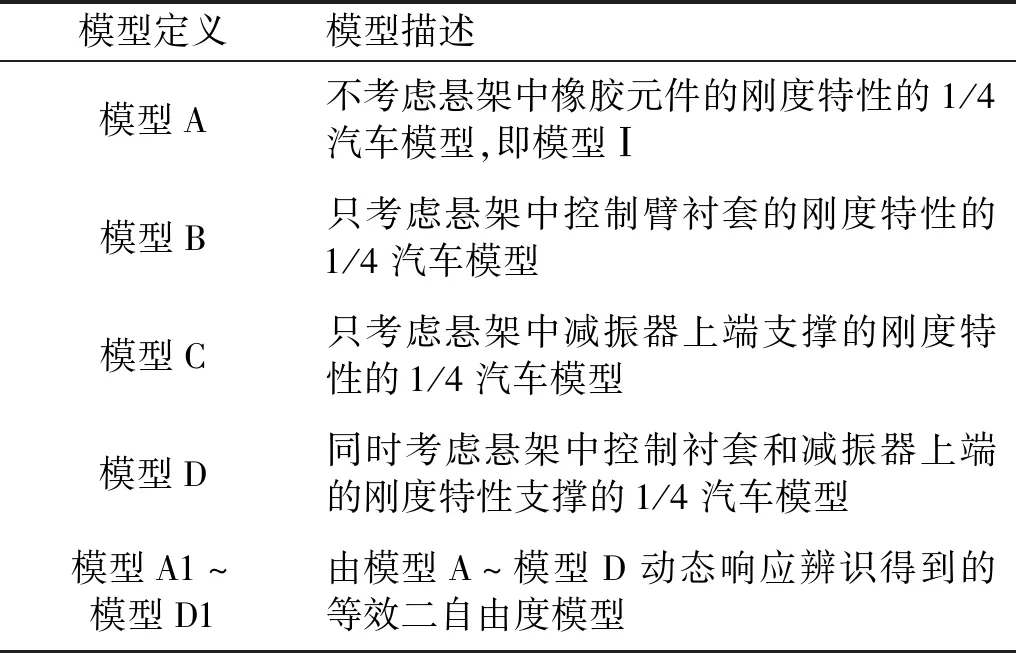
表5 不同的1/4汽车模型及对应的等效二自由度模型的定义Tab.5 Definitions of different quarter-car model and the corresponding equivalent 2DOFs model

由表6可知，悬架中橡胶元件的刚度特性主要影响二自由度模型中悬架刚度和阻尼系数的辨识结果，而对质量参数的影响较小。控制臂衬套对等效二自由度模型中悬架刚度的辨识结果有明显的影响，模型B1的悬架刚度数值相对于模型A1增加了20%，模型C1的悬架刚度数值相对于模型A1减少了10%。由此可见，控制臂衬套会使等效二自由度模型的悬架刚度数值加大，而减振器上端支撑会使等效二自由度模型的悬架刚度数值减小。总体上，模型D1的悬架刚度数值相对于模型A1增加了13%。

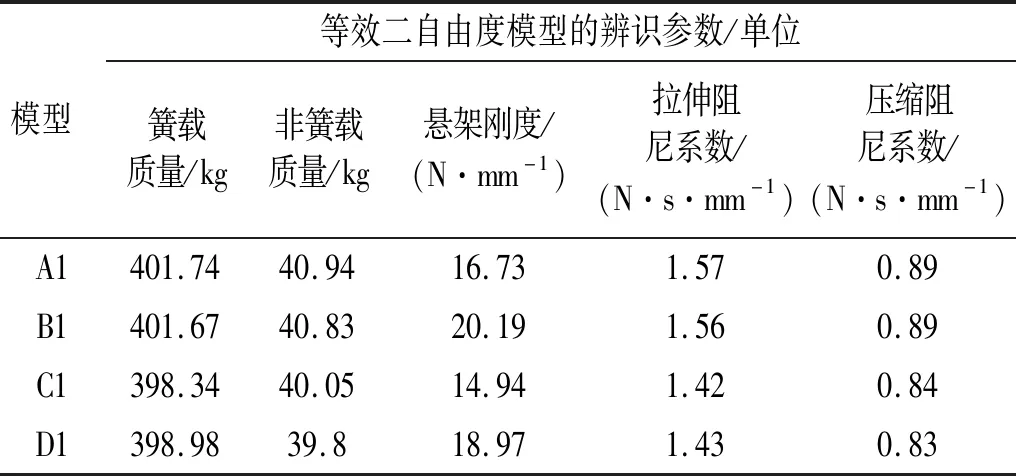
表6 等效二自由度模型质量、刚度与阻尼系数的辨识结果Tab.6 Identified mass,stiffness and damping coefficients of the equivalent 2DOFs model

等效二自由度模型B1的阻尼系数数值与等效二自由度模型A1的辨识结果基本一致，而模型C1和模型D1的拉伸阻尼系数和压缩阻尼系数的数值基本一致，相对于模型A1的拉伸阻尼系数和压缩阻尼系数的数值分别减少了9%和6%左右。可见，控制臂衬套对辨识参数结果中的阻尼系数的数值基本没有影响，而减振器上端支撑将会减小辨识参数结果中的阻尼系数的数值。

等效二自由度模型悬架刚度数值的变化将影响簧载质量与非簧载质量的固有频率。求出模型A1～模型D1的悬架偏频和簧载质量加速度与轮胎动载荷的频率响应曲线，如表7和图6所示。表7结果表明，悬架橡胶元件的刚度特性主要影响等效二自由度模型的簧载质量固有频率，而对非簧载固有频率影响不大；图6结果表明，悬架橡胶元件的刚度特性主要影响等效二自由度模型在簧载质量固有频率附近簧载质量加速度和轮胎动载荷的响应特性。

因此，下文进行基于等效二自由度模型的参考模型滑模控制研究时，仅采用等效二自由度模型D1的参数辨识值和名义值。

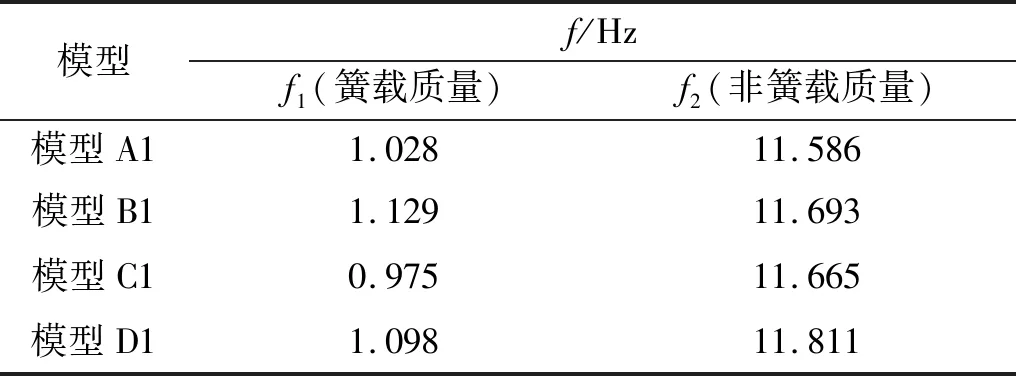
表7 模型A1～模型D1的悬架偏频Tab.7 Nature frequency of model A1—modele D1

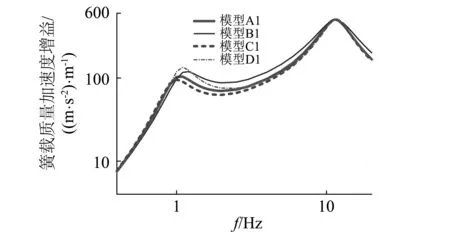
(a)簧载质量加速度

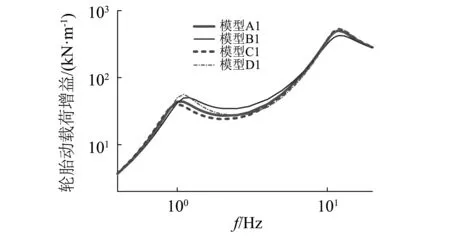
(b)轮胎动载荷图6 模型A1～模型D1的频率响应曲线对比Fig.6 Dynamic responses of model A1—model D1 in frequency domain

3 基于等效二自由度模型的参考模型滑模控制

3.1 基于参考模型的滑模控制算法

基于参考模型的滑模控制的基本原理是采用适当的控制力来使二自由度控制模型和参考模型的运动保持一致，优点在于参考模型不必是一个实际的系统，可以是任何理想的数学模型。

本文设计的二自由度控制模型控制力由一种基于参考模型的滑模变结构控制器产生，如图7所示。由图7可知，二自由度控制模型只是在二自由度模型的基础上，增加了簧载质量和非簧载质量之间的控制力；参考模型在二自由度模型的基础上在簧载质量与理想固定端之间增加了一个阻尼系数csky，构造理想的天棚控制，以衰减簧载质量的振动，从而获得良好的行驶平顺性。

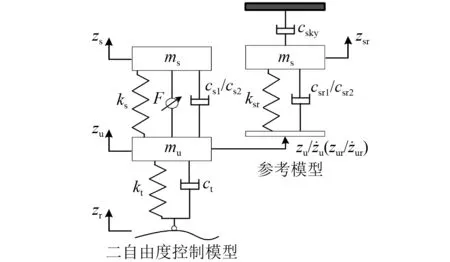
图7 基于参考模型的二自由度控制模型Fig.7 2DOFs control model based on the reference model

由于实际路面信号较难测量，参考模型不考虑二自由度模型的轮胎刚度和轮胎阻尼，以二自由度控制模型的非簧载质量的位移和速度信号作为参考模型的输入，使二自由度控制模型的簧载质量跟踪参考模型的簧载质量运动。

二自由度控制模型的运动微分方程为

(14)

式(14)中的阻尼系数cs定义为

(15)

参考模型运动微分方程为

(16)

式(16)中的阻尼系数csr定义为

(17)

定义二自由度控制模型与参考模型中簧载质量位移差和速度差为误差矢量e

(18)

对误差矢量进行滑模控制，建立滑模面函数[17]

s=Ce

(19)

C=[h,1]

(20)

式中:h为大于0的常数。

(21)

(22)

在满足广义滑模条件的前提下，采用指数趋近率来改善滑动模态的运动品质，可得

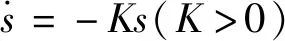
(23)

式中：K为指数趋近率参数，适当调大K值能保证快速到达滑模切换面。

将式(23)代替式(21)，即可得到二自由度控制模型的主动控制力

F=Fdeq+msKs

(24)

3.2 参考模型的参数对滑模控制效果的影响分析

第3节的计算结果已经表明，等效二自由度模型D1中的刚度和阻尼系数的数值和名义值的差异相差较大，而质量参数的数值与名义值的差异可以忽略不计。因此，当参考模型中采用的刚度和阻尼系数的数值与二自由度控制模型不一致时，将影响二自由度控制模型的控制效果。根据式(14)和式(24)，搭建Matlab/Simulink仿真框图，在式(12)的位移阶跃输入下，求解出簧载质量和控制力的响应。为了下文叙述方便，对参考模型中的刚度和阻尼系数采用不同数值时的二自由度控制模型进行定义，如表8所示。

表8 等效二自由度控制模型的参考模型定义Tab.8 Definitions of reference model based on the 2DOFs control model

参考模型采用的理想天棚控制，可以抑制簧载质量振动，但会加剧非簧载质量的振动。因此，参考模型中的理想天棚阻尼系数csky的数值需要综合考虑簧载质量和非簧载质量的振动控制目标，进行优化得到。由于本文只研究参考模型参数采用不同数值时，二自由度控制模型的簧载质量加速度和控制力的响应情况，因此，天棚阻尼系数csky只需取一个适中的数值。

仿真时，二自由度控制模型的质量、刚度和阻尼系数采用模型D1的辨识值，参考模型的参数数值根据表8设置，h,K和csky分别为10,50和3 N·s/mm。

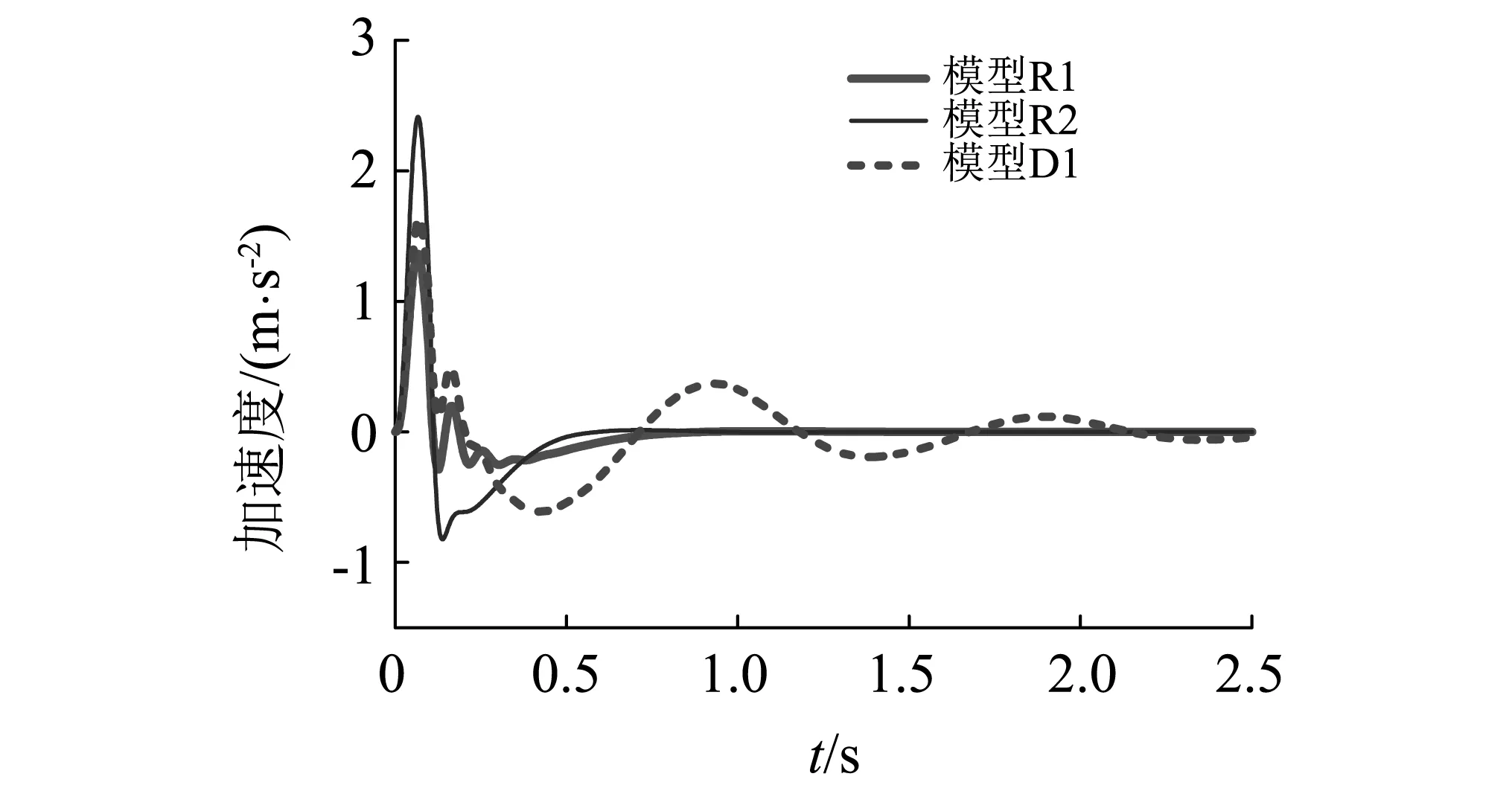
基于参考模型R1和R2的滑模控制效果见图8。由图8可知，采用基于参考模型的滑模控制可以很好地衰减簧载质量的振动。但是与基于参考模型R1相比，基于参考模型R2的二自由度控制模型的簧载质量加速度响应较大，并且需要提供更大的控制力。因此，采用基于参考模型的滑模控制时，参考模型的刚度和阻尼系数的数值应尽可能地与二自由度控制模型中相关参数的数值一致。

4 参考模型参数对滑模控制效果的影响的试验验证

参考模型的刚度和阻尼系数对二自由度控制模型的控制效果的影响情况，通过Quanser-Active Suspension试验设备[18]进行验证。试验设备中的二自由度控制模型如图9所示，主要由簧载质量、非簧载质量、悬架弹簧、轮胎弹簧和两个电机(3，6)组成。

位于底部的电机(6)产生位移输入，中部的电机(3)产生控制力，每个电机都带有转角位移编码器，测量输入位移和悬架相对位移。另外，还有一个编码器和加速度传感器固定在簧载质量上，分别测量簧载质量的位移和加速度。该二自由度控制模型没有安装阻尼装置，将运动过程中直线轴承与导轨之间摩擦力以阻尼力代替，其阻尼系数及模型的参数如表9所示。试验时，参考模型中的天棚阻尼系数csky取值为30 N·s/m，二自由度控制模型的路面输入为式(12)。

(a)簧载质量加速度

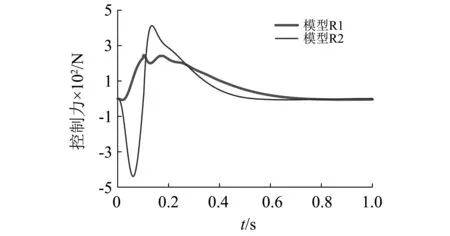
(b)控制力图8 采用参考模型R1和R2时，二自由度控制模型的簧载质量加速度和控制力的响应Fig.8 Sprung mass acceleration and control force of the 2DOFs control model under reference model R1 and R2

1-簧载质量；2-非簧载质量；3-控制电机；4-悬架弹簧；5-轮胎弹簧；6-位移输入电机图9 二自由度控制模型实物图Fig.9 Diagram of the 2DOFs control model

为了证明第4.2节中参考模型参数与二自由度控制模型不一致时，滑模控制的效果会变差的仿真结论。根据表10的方案分别进行试验，试验得到二自由度控制模型的簧载质量加速度和控制力的响应，如图10所示。

表9 二自由度控制模型参数Tab.9 Parameters of the 2DOFs control model

表10 二自由度控制模型试验方案Tab.10 Measured schemes of the 2DOFs control model

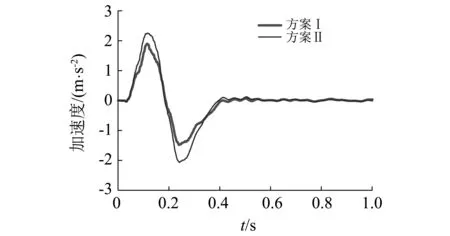
(a)簧载质量加速度试验值

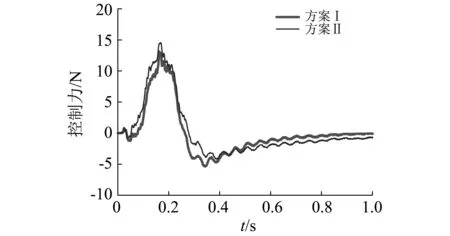
(b)控制力试验值图10 试验方案Ⅰ和方案Ⅱ得到的二自由度控制模型的簧载质量加速度和控制力的响应Fig.10 Sprung mass acceleration and control force of the 2DOFs control model under measuring schemes Ⅰ and Ⅱ

试验方案Ⅱ得到二自由度悬架模型的簧载质量加速度和控制力的响应幅值比试验方案Ⅰ得到的响应幅值大。因此，证明了在基于参考模型的滑模控制中，当参考模型的刚度和阻尼系数与二自由度控制模型的参数一致时，可以获得更好的控制效果的仿真结论。

5 结 论

(1)在ADAMS中建立了基于双横臂悬架的1/4汽车模型，并根据其簧载质量和非簧载质量的动力学响应，辨识出等效二自由度模型的质量、刚度和阻尼系数。等效二自由度模型辨识结果中的刚度和阻尼系数的数值和1/4汽车模型中相关参数的名义值有较大的差异。

(2)橡胶元件的刚度特性主要影响等效二自由度模型辨识结果中的悬架刚度和阻尼系数。控制臂衬套的刚度特性会使悬架刚度加大，而减振器上端支撑的刚度特性会使悬架刚度减小；控制臂衬套的刚度特性对阻尼系数基本没有影响，而减振器上端支撑的刚度特性将会减小阻尼系数。

(3)建立采用辨识参数的二自由度控制模型，构造基于参考模型的滑模控制器产生控制力。试验和计算结果都表明，与采用名义值相比，参考模型的刚度和阻尼系数采用辨识值时，等效二自由度控制模型可以获得更好的控制效果。