GGA+U法研究稀土(La、Ce、Pr、Nd)掺杂对ZnO电子结构和光学性质的影响

雷博程，刘桂安，王少霞，赵旭才，毛著鹏，夏 桐，黄以能,2，张丽丽,2

(1.伊犁师范大学物理科学与技术学院，新疆凝聚态相变与微结构实验室，伊宁 835000；2.南京大学物理学院，固体微结构物理国家重点实验室，南京 210093)

1 引 言

氧化锌(ZnO)是一种直接宽带隙半导体材料，其禁带宽度为3.37 eV，自由激子结合能为60 meV，属于Ⅱ-Ⅳ族半导体材料[1]。因其具有高的激子束缚能[2]，使ZnO在制作透明导电氧化物薄膜(ITO)、压敏陶瓷、气敏材料、探测器、稀磁半导体材料等方面表现优异[3-5]，尤其在短波长半导体发光器件的制造中有着重要的应用前景，已经引起广大研究人员的热切关注[6-7]。

由于稀土元素原子具有特殊的电子层结构，同时具有电价高、原子半径大、化学性活泼、氧化物的热稳定性等特点[8-9]，能更有效的调节ZnO电子结构和光电性能，所以稀土元素逐渐成为ZnO掺杂体系的研究重点。比如：Wu等[10]研究发现，掺杂稀土La后体系的稳定性增强，带隙变宽；其费米能量进入导带，呈现出金属性并转变为简并半导体。李春萍等[11]发现，Au，N共掺杂ZnO仍为直接带隙半导体，但带隙减小，有利于p型ZnO的形成；在光学性质中，掺杂后的可见光和紫外区域都有很大的增强。Berrezoug等[12]采用FP-LAPW方法，发现ZnO的带隙为3.27eV，随着掺入Ga浓度的增加，使费米能级附近的导带中产生了浅能级Ga-4s态，增加了光学带隙和导电性；在介电函数的虚部中吸收边缘移动到更高的能级，并且静态折射率和反射率都增加。Li等[13]采用GGA+U方法，发现掺杂O空位的La不会引起ZnO铁磁性，而具有Zn空位的La掺杂ZnO具有铁磁性；净磁矩主要与O的2p态不成对电子量有关；形成能也显示La掺ZnO容易产生Zn空位。Jia等[14]采用GGA+U方法，与纯ZnO相比，Ce的掺入使带隙变窄，吸收光谱呈现红移；杂质体系的铁磁性随着Ce掺杂浓度的增加而增加，主要归因于Ce-4f，Ce-5d和O-2p态的杂化耦合效应。Wen等[15]研究发现，Nd掺杂使ZnO成为n型半导体，在费米能级处呈现占据状态，主要由Nd的4f态贡献，且体系的吸收峰红移，并增强可见光的吸收。

综上所述，稀土元素掺杂的方法对ZnO光学性质的调节很有效，但大多针对单一稀土掺入进行研究，未系统的研究系列稀土元素(比如：La、Ce、Pr、Nd)的掺杂对ZnO光电性质的影响，所以本文将对La/Ce/Pr/Nd掺杂ZnO进行更为细致的第一性原理计算，以期望对相关实验的研究提供理论依据和参考。

2 结构模型和参数设置

本文基于Masterial Studio 8.0中的密度泛函理论的第一性原理，利用CASTEP[16]模块完成的。本文采用GGA+U[17-20]的方法进行修正带隙，Zn的3d电子加U值是4.64，O的2p电子加U值是8.12[21]，La、Ce、Pr、Nd的4f的加U值为6 eV[22-23]。用广义梯度近似PBE泛函来处理电子和电子之间相互作用的交换关联能，平面波截断能Ecut=340 eV，自洽收敛精度设为平均每个原子为2.0×10-5eV/atom，布里渊区时K点选取2×2×2，所有计算都在倒格矢空间进行。

本文以ZnO为本征体，其空间群为P63m(No.186)，属于六方纤锌矿结构，晶格常数a=b=0.325 nm，c=0.520 nm；α=β=90°，γ=120°[24]，主要研究的几种元素电子组态分别为：Zn(3d104s2)，O(2s22p4)，La(5d16s2)，Ce(4f15d16s2)，Pr(4f36s2)，Nd(4f46s2)，晶胞原子坐标分别为 Zn(0.3333，0.6667，0)，O(0.3333，0.6667，0.3825)[25]，本文建立2×2×1超胞模型，稀土元素将替代体心的Zn原子，建立纯Zn8O8和Zn7XO8超晶胞(其中X=La、Ce、Pr、Nd)，掺杂前后晶体模型如图1所示。

图1 (a)纯ZnO和(b)Zn7XO8结构模型(X=La/Ce/Pr/Nd))Fig.1 (a)Pure ZnO and (b)Zn7XO8 structural model(X=La/Ce/Pr/Nd))

3 La/Ce/Pr/Nd掺杂ZnO的结果与分析

3.1 晶格结构和稳定性分析

为了研究Zn7XO8(X=La/Ce/Pr/Nd)体系形成的难易程度，计算了掺杂后体系的形成能。本文中掺杂形成能Ef由下面公式[26-27]计算给出:

Ef=E(doped)-E(perfect)-∑iniEi

(1)

其中Ef是掺杂形成能，E(doped)是缺陷晶体的总能量，E(perfect)是完美晶体的基态能量，∑i表示移除的原子时为正数，加入的原子时为负数，ni(i为La/Ce/Pr/Nd)是晶胞中增加或减少的原子个数，Ei为原子i所对应的能量值。Zn7XO8体系的形成能都为负值(表1)，表明缺陷可以自发的形成，且形成能与基态能量随掺入元素的半径的减小而减小，表示体系越来越稳定；其中Zn7NdO8体系的形成能最小，表明Nd更容易制备调制掺杂结构。

根据布局数的概念，键布局数为正，说明原子之间是成键的，且高值表示键为共价键，低值表示原子之间是离子相互作用；键布局数为负，说明原子之间是反键，即不成键[28-30]。掺入稀土元素后，各体系的最大与最小Zn-O键布局数随稀土元素原子电荷数的增加有增大的趋势，其共价性也有相同的变化趋势，说明Zn-O的共价性的强弱与杂质掺入原子的序数成正比[31-32]，并且各体系的基态能量在不断地减小，进一步说明随杂质原子电荷数的增大，掺杂体系的形成容易程度及稳定性也都增强。

从表1还可以发现，掺入杂质原子后，Zn原子与O原子之间的键长相比于未掺杂的键长变化非常小。由最大及最小Zn-O键长数据可知，掺入稀土元素后，随着稀土元素原子电荷数的增大而减小，证明掺杂体系发生了一定程度的畸变，主要是因为RLa(0.274 nm)>RCe(0.270 nm)>RPr(0.267 nm)>RNd(0.264 nm)>RZn(0.153 nm)，原子半径的大小和原子电荷数相反，体积的变化也是如此。当X(La/Ce/Pr/Nd)占据Zn位置后，ZnO晶格会膨胀，并且随着原子半径的增加，其畸变的强度就越强，这将导致ZnO原有的晶体对称性被破坏，正负电荷中心不再重合，而产生局域电势差，有利于阻碍光生空穴和电子对的复合，进而有望提高材料的光催化性能。这将在光吸收谱图中得到验证，说明杂质原子进入后，原子间的电子壳层重叠加剧，加剧了原子间的电子转移，共有化增强。

表1 各模型的能量，形成能，键布居，键长与体积Table 1 Energy, formation energy, bond population, bond length and volume of each model

3.2 掺杂前后的电子结构

本文采用GGA+U的方法进行修正带隙，图2(a)为纯ZnO的能带结构图，图中的G、F、Q、Z、G为布里渊区高对称点，计算修正后ZnO单胞带隙为3.375 eV，与实验值3.37 eV[33]基本一致，与Berrezoug[12]和Al-Sunaidi[34]计算得到的禁带3.27 eV、0.600 eV相比，本实验得到的结果与实验值的差距最小，故计算所选取的参数设置是可靠的。从图2(b、c、d、f)中可以看出，跃迁方向都为G-G，跃迁类型都为直接跃迁；而掺杂体系的禁带宽度分别为3.791 eV、3.388 eV、3.669 eV、3.559 eV，其中Zn7PrO8、Zn7NdO8体系有杂质能级出现，分别为0.019 eV、0.069 eV；掺杂体系的能级数目明显增多，导带整体下移，能级变得密集，使得价带也整体下移。

对比于纯的ZnO的能带图，掺杂稀土元素La/Ce/Pr/Nd后，随着原子的半径减小，La、Ce、Pr、Nd的禁带宽度都增大，其中Nd杂质能级最大，说明可能发生能级跃迁的电子数目增多，更易跃迁，对应于态密度图，主要由于Nd的4f态做贡献。

从图3(a)的Zn8O8能态图中可以分析出，Zn原子的3d态和O原子的2p态均在费米能级附近达到峰值，形成p-d杂化。图3(b)的Zn7LaO8能态图中分析出，Zn-3d态、O-2p态和La-5d态均在费米能级附近达到峰值，形成p-d杂化。从图3(c)的Zn7CeO8能态图中分析出，Zn-3d态、O-2p态、Ce-4f态和Ce-5p态均在费米能级附近达到峰值，形成p-d和p-f杂化。从图3(d)的Zn7PrO8能态图中分析出，Zn-3d态、O-2p态、Pr-4f态和Pr-5p态均在费米能级附近达到峰值，形成p-d和p-f杂化。从图3(e)Zn7NdO8能态图中分析出，Zn-3d态、O-2p态、Nd-4f态和Nd-5p态均在费米能级附近达到峰值，形成p-d和p-f杂化。对应于能带图发现，掺入Pr和Nd元素后，有杂质能级的出现，主要由稀土元素的4f态贡献。

图2 能带结构图Fig.2 Band structure diagram

图3 能态密度图Fig.3 Energy density of states diagram

3.3 掺杂前后的光学性质分析

图4为纯ZnO和Zn7XO8体系的吸收光谱，在光学计算中，本文也利用了GGA+U 的方法进行修正带隙。从图中可得纯ZnO的光吸收边约为2.831 eV。而掺杂稀土元素La/Ce/Pr/Nd后，使得体系的实际带隙变窄，价带顶存在少量空穴，空穴的存在使得部分电子的带间跃迁成为可能，从而能够吸收更多较低能量的光子，所以导致掺杂体系的吸收边均为0.01 eV，体系的吸收边都向低能方向移动，发生了红移，增强了对可见光的响应范围，稀土元素的掺入有利于ZnO体系光催化功能的提高。其中Zn7LaO8体系在可见光区域的峰值最高，这是因为Zn7LaO8体系在各掺杂体系中实际禁带宽度最小，其电子由价带激发至导带所需的跃迁能量最小，由此可知Zn7LaO8是各掺杂体系中光催化功能最强的体系。

图5是纯ZnO和Zn7XO8体系介电函数的实部曲线图，其对应于介电常数随入射光能量的变化[35]。介电常数表征了介质在外电场作用下极化程度的量，也就是对电荷的束缚能力，介电常数越大，对电荷的束缚能力越强[36-39]。在无入射光情况下，静态介电常数为实部的纵坐标，从图中可以得到纯ZnO的静态介电常数值为1.874，随着光子能量的增加，在3.595 eV和8.473 eV处形成了峰值；掺杂稀土元素La、Ce、Pr、Nd后，静态介电常数值分别为6.143、4.033、3.671、2.727，随着光子能量的增加，分别在7.229 eV、7.054 eV、8.015 eV、8.144 eV处形成了峰值，对比纯ZnO介电函数的较强峰值，随着La/Ce/Pr/Nd原子的半径的减小，体系的静介电常数值减小，极化能力变小，进而光生电场强度变小，对电荷的束缚能力减弱，其中La的介电函数值最大，极化能力最强。

介电函数虚部与声子晶格振动有关，表示介电损耗，对应着电子的带间跃迁。图6是纯ZnO和Zn7XO8体系介电函数的虚部图，首先可以看出纯ZnO主峰在12.763 eV处，主要由价带顶O的2p态和导带底Zn的4s态之间的电子跃迁引起的，掺杂体系较纯ZnO的峰值都向低能方向移动(红移)，与带隙的变化趋势一致。当La掺入后，主峰在8.615 eV处，主要由价带顶O的2p态、Zn的3d态和导带底La的5d态之间的电子跃迁引起的；当Ce掺入后，主峰在8.681 eV处，主要由价带顶O的2p态、Zn的3d态和导带底Ce的4f态之间的电子跃迁引起的；当Pr掺入后，主峰在9.427 eV处，主要由价带顶O的2p态、Zn的3d态和导带底Pr的4f态之间的电子跃迁引起的；当Nd掺入后，主峰在9.515 eV处，主要由价带顶O的2p态、Zn的3d态和导带底Nd的4f态之间的电子跃迁引起的，所以可以得到掺杂后的介电函数图要比不掺杂时存在很多不显著的折叠态，这是因为在晶体的能带结构中，对同一峰值可能会由直接或间接的多能级跃迁造成。

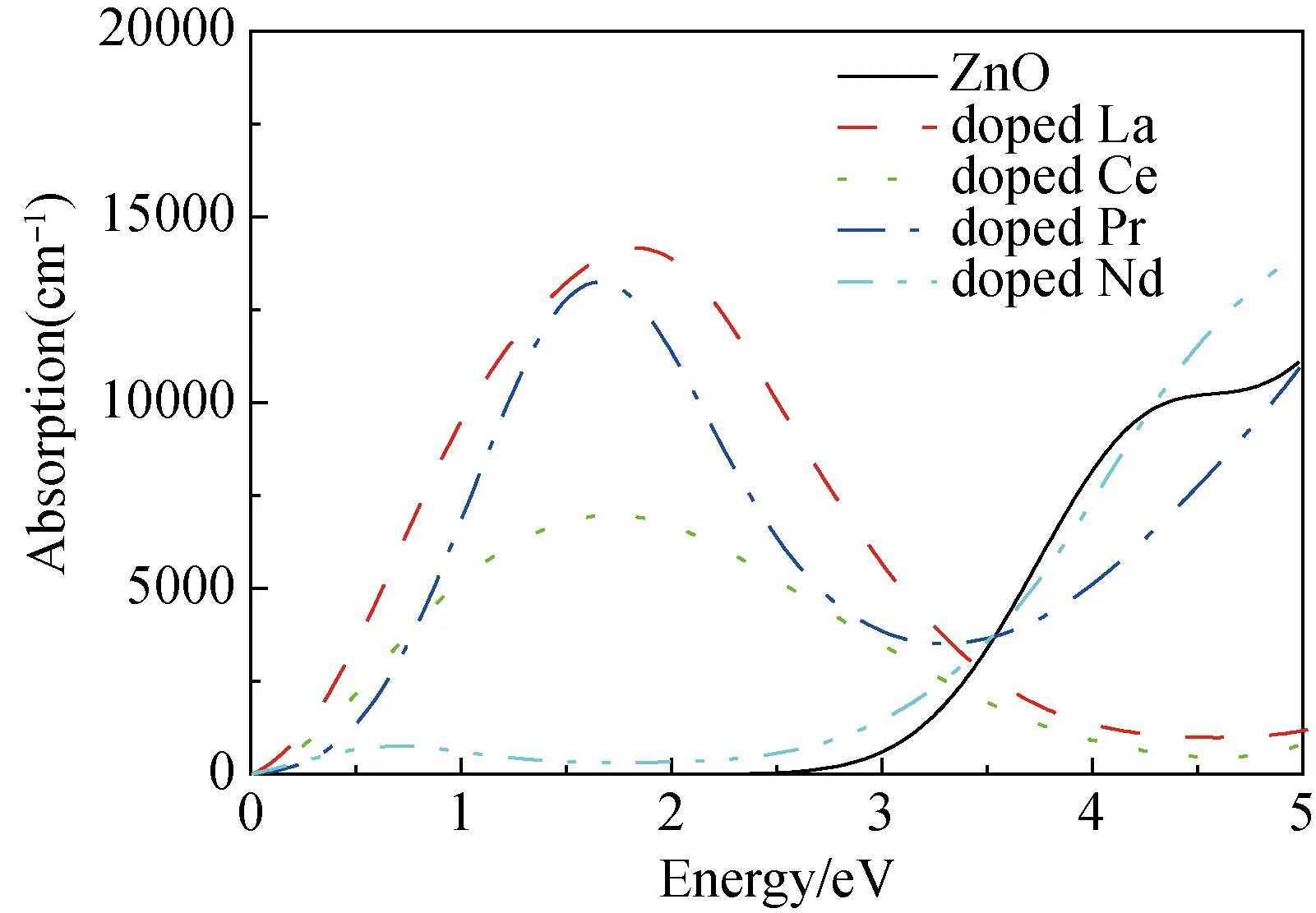
图4 纯ZnO和Zn7XO8吸收光谱图(X=La/Ce/Pr/Nd))Fig.4 Absorption spectra of pure ZnO and Zn7XO8(X=La/Ce/Pr/Nd))

图5 纯ZnO和Zn7XO8介电函数实部图(X=La/Ce/Pr/Nd))Fig.5 Real part diagram of pure ZnO and Zn7XO8 dielectric function(X=La/Ce/Pr/Nd))

图6 纯ZnO和Zn7XO8介电函数虚部图(X=La/Ce/Pr/Nd))Fig.6 The imaginary part of the dielectric function of pure ZnO and Zn7XO8 (X=La/Ce/Pr/Nd)

4 结 论

在本文中，采用第一性原理密度泛函理论下的GGA+U方法，以ZnO作为本征体，建立了2×2×1的超晶胞模型，选取了La、Ce、Pr、Nd四种元素作为掺杂原子进行计算。分析讨论了掺杂前后体系的晶体结构、电子结构和光学性质，基于计算结果发现：

(1)在晶体结构方面，各体系总能量随掺杂原子(La/Ce/Pr/Nd)的电荷数的增加而减小，与形成能的变化规律一致，其中Zn7NdO8体系的能量以及形成能都是最低，说明该体系的稳定性最好、易于制备。各掺杂体系的最大与最小Zn-O键布局数，随着原子的电荷数依次增加也有增大的趋势，表明其共价性也是这样变化。各掺杂体系的最大及最小Zn-O键长，它们都是随着杂质原子半径的增大而增大，证明掺杂体系发生了较强的畸变，但抑制了光生空穴和电子对的复合，有望提高材料的光催化性能。

(2)在电子结构方面，掺杂元素La/Ce/Pr/Nd后，体系的跃迁类型没变，仍为直接跃迁，随着原子(La/Ce/Pr/Nd)的半径减小，La、Ce、Pr、Nd的禁带宽度都增大；对应于态密度图，体系都形成p-d和p-f杂化轨道，而掺入Pr和Nd元素后，有杂质能级的出现，电子更易跃迁，主要原因在于稀土元素的4f电子态。

(3)在光学性质方面，掺杂元素La/Ce/Pr/Nd后，体系的吸收边都向低能方向移动，发生了红移，其中La掺杂体系的红移程度最高；各掺杂体系的静介电值都比纯ZnO的大，其中Zn7LaO8的最大，说明该体系的极化能力最强，说明其光生电场强度最强，光激发载流子在晶体内的迁移变快，对电荷的束缚能力增强。