实际晶体的生长机制
闵乃本
(南京大学固体微结构物理国家重点实脸室,南京 210008)
1 引 言
理想晶体是由一层层互不连通的原子面堆垛而成。基于这种内禀性质,Gibbs于1878年指出晶体生长不是一个连续过程,当一层原子面填满后,必须克服一客观存在的热力学势垒,才能开始次层的生长[1],这被后人称之为二维成核势垒。Frank于1949年指出如果晶体的内禀结构不是由一层层严格平行于生长面的原子面构成,在晶面上就可能出现永不消失的台阶,在这种情况下,晶体生长将是一个连续过程[2-4]。螺型位错在表面的露头处可提供一永不消失的台阶,虽然Farnk当时就指出,能提供永不消失台阶的位错不一定必须是螺型位错[2-4],然而迄今人们只对螺位错机制有较深刻的理解。Bauser于1984年也争辩说,在考虑晶体生长时,位错线的方向不具有任何意义[5]。近年来的实验观察结果表明,除螺型位错外,刃型位错、层错、孪晶都能成为生长台阶源[6-10]。自1988年以来,我们对晶体生长的缺陷机制完成了较为系统的工作[11-16],本文对此作一简要的评述。
2 晶体生长的位错机制
如前所述,理想晶体是由一层层相互平行的原子面堆垛而成,因而在表面不存在永不消失的台阶。在实际晶体中,位错的长程应变场使晶面扭曲,使某些原来相互平行、互不连通的原子面转变成单一的螺蜷面或是多重螺蜷面,这样在某些表面将出现永不消失的台阶。若表面与位错线相交,且该表面不处于以位错的伯格斯矢量为轴的晶带中,则位错在该表面的露头将存在永不消失的台阶,而不管位错线的取向如何,亦即,不论位错是刃型、螺型还是混合型。为了说明这一性质与位错线的取向无关,我们讨论纯刃型位错产生的永不消失的台阶。设想一个产生位错的Volterra过程[17]并参阅图1,将一立方晶体沿平行于(010)面的ABCD面切开;加外力使割面两岸沿[010]方向相对位移,位移矢量为b=a[010],a为晶格常数;用同样物质的原子面ABCD填满割面两岸位移所留下的空隙,并除去外力。于是在所填充的“半”原子面的边缘AB处产生了位错,其伯格斯矢量为b=a[010],位错线平行于[100],此为纯刃型位错。让我们关注于相对(110)点阵面的原子位移,可以看出割面左边的原子相对于(110)面向上位移,而割面右边的原子相对于(110)面向下位移。由于位移关于(110)面的法向分量正好与(110)面的面间距相等,因而任一(110)面在晶体中割面处正好与次层相接。这样通过Volterra过程在晶体中引入纯刃型位错后就使原相互平行、互不连通的(110)点阵面转变为一螺蜷面,而此螺蜷面在(110)表面的露头处即为一永不消失的台阶,参阅图1。于是该晶体的(110)面的生长过程,就是该台阶绕位错在(110)面上露头点的旋转过程,也是构成晶体的螺蜷面的延伸过程。这样,理想晶体生长所需克服的二维成核位垒完全消失,晶体生长成为一连续过程,相应的生长动力学规律也由指数律转变为抛物线律。图2(a)显示了伯格斯矢量为[010]a;位错线方向沿[100]的纯刃型位错,图2(b)显示了具有同样伯格斯矢量但位错线沿[010]的纯螺型位错。我们关注于这两种不同的位错对晶体的内部结构和表面原子组态的影响。从图2可以看到,这两种位错具有相同的伯格斯矢量但不同的位错取向;尽管位错线的取向不同,都使晶体中(110)点阵面从无限多层相互平行、互不连通的原子面转变为单一螺蜷面,都在(110)表面形成了永不消失的台阶。因而,对晶体生长而言,只要晶面与位错相交,只要晶面不处于以该位错的伯格斯矢量为轴的晶带中,不管位错线的取向如何,亦即不管位错为螺型、刃型还是混合型,位错对晶体生长的贡献都是相同的,若晶面与位错线相交但处于以位错的伯格斯矢量为轴的晶带中,在晶体中平行于该晶面的点阵面仍然是一层层互不连通、相互平行的原子面。这是由于位错在晶体中所引起的原子位移与该类晶面平行,并不引起该类点阵面的畸变,因而在该类晶面上不存在永不消失的台阶,该类晶面的生长仍需通过二维成核过程。
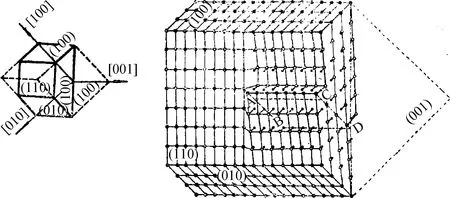
图1 简单立方晶体的(110)面上由位错线平行于[100]、伯格斯矢量为[010]的纯刃型位错所引起的永不消失的台阶;注意通过引入位错,点阵面(110)转变为单一的螺蜷面Fig.1 Creation of a pure edge dislocation by Voltarra’s process and self-perpetuating step on a (110) growth surface of a simple cubic crystal resulted from a pure edge dislocation parallel to [100] with Burgers vector [010] and the dislocated planes transformed into a single helicoid
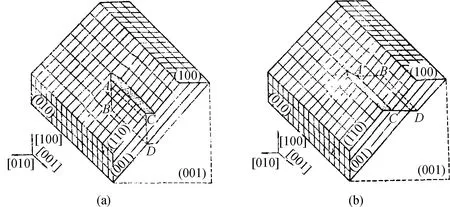
图2 纯刃位错与纯螺位错在简单立方晶体(110)面上产生的永不消失的生长台阶的比较(a)位错线平行于[100]、伯格斯矢量为[100]的刃型位错在(110)面上产生的台阶;(b)位错线平行于[010]、伯格斯矢量为[010]的螺型错位在(110)面上产生的台阶Fig.2 Comparison of the self-perpetua-ting steps on (110) surface of a simple cubic crystal resulted from a pure edge dislocation with that resulted from a pure screw dislocation (a)self-perpetuating step resulted from a pure edge dislocatlon parallel to [100] with [010] Burgers vector:(b)self-perpetuating step resulted from a pure screw dislocation parallel to [010] with [010] Burgers vector
3 晶体生长的层错机制
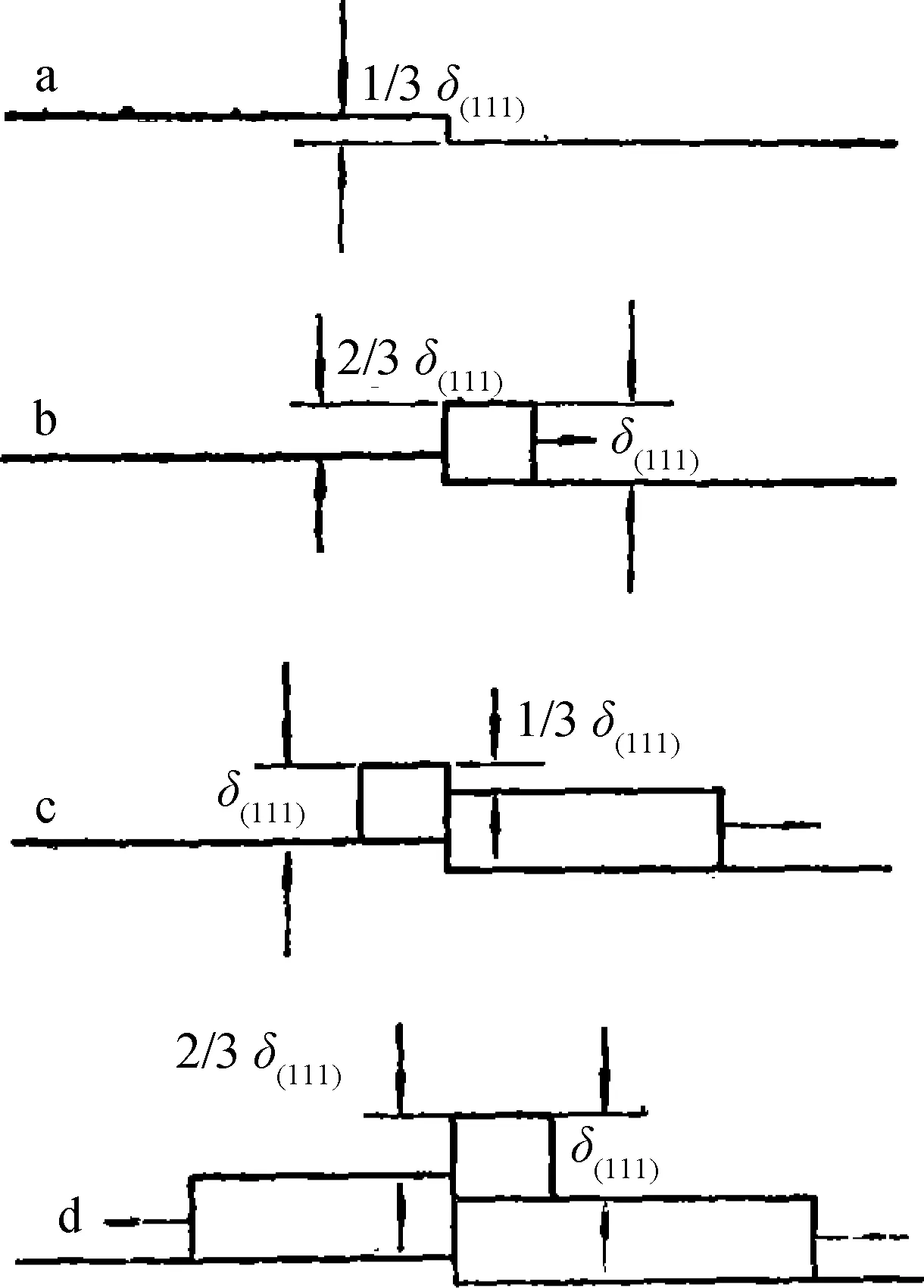
图3 层错机制在面心立方晶体(111)面上产生生长台阶的过程(a)层错露头处高度为(l/3)δ(111)的亚台阶;(b)当一列原子吸附于亚台阶上,全台阶与第二类高为(2/3)δ(111)的亚台阶在两侧同时产生;(c)当一列原子吸附于第二类亚台阶、第一类亚台阶与另一全台阶同时产生;(d)上述事件无限重复、全台阶交替地产生于两侧Fig.3 Step generation mechanism of stacking fault on (111) surface of a fcc crystal (a)sub-step with heigbt of (1/3)δ(111);(b)when a row of atoms is adsorbed along the sub-step, a full-step and a sub-step with (2/3)δ(111) are created;(c)after a row of atoms is adsorbed at the sub-step of second type, a sub-step of first type and another full-step appear;(d)the event repeated alternatively full-step will be produced continuously
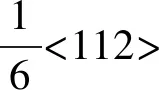

表1 面心立方晶体中层错在(111)生长面产生的亚合阶离度Table 1 Height of self-perpetuating sub-steps on (111) surface of fcc crystal
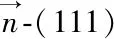

图4 面心立方晶体(111)面上亚台阶的原子组态(a)高度为(1/3)δ(111)的亚台阶;(b)高度为(2/3)δ(111)的亚台阶及全台阶Fig.4 Atomic configuration of a self-perpetuating sub-step(a)sub-step with(1/3)δ(111)in height;(b)sub-step with (2/3)δ(111) and full-step
在此基础上,闵乃本及其合作者进行了细致的分析,得出了层错机制的单核模型(mononuclear model)和多核模型(birth and spread model)的生长动力学,并和二维成核机制进行了对比[12,14]。若RL是层错机制提供的生长速率,Ra为二维成核机制提供的生长速率,在典型的生长条件下[12],两种机制所提供的生长速率比值的对数与过饱和度△μ/kT的关系示于图5。曲线1是层错机制的多核模型的生长速度与二维成核机制的对比结果,曲线2 是单核层错机制与二维成核机制的对比。由曲线1可以看出,ln(RL/Ra)>0,这表明在整个过饱和度的变化区间内有RL>Ra,亦即多核模型的层错机制所提供的生长速率始终大于二维成核所提供的。曲线2表明只在△μ/kT<2.4的条件下,单核层错机制的生长速率才大于二维成核。现将在不同的过饱和度的区间内三种不同的模型所提供的生长速率的大小顺序表述如下:当△μ/kT<1.7时,单核层错机制>多核层错机制>二维成核机制;当1.7<△μ/kT<2.4时,多核层错机制>单核成错机制>二维核机制;当△μ/kT>2.4时,多核层错机制>二维成核机制>单核层错机制。显然,在整个过饱和度变化区间内,层错机制总是优于二维成核机制,但在低过饱和度下,单核层错机制优先,而在高过饱和度下,多核层错机制占优势。
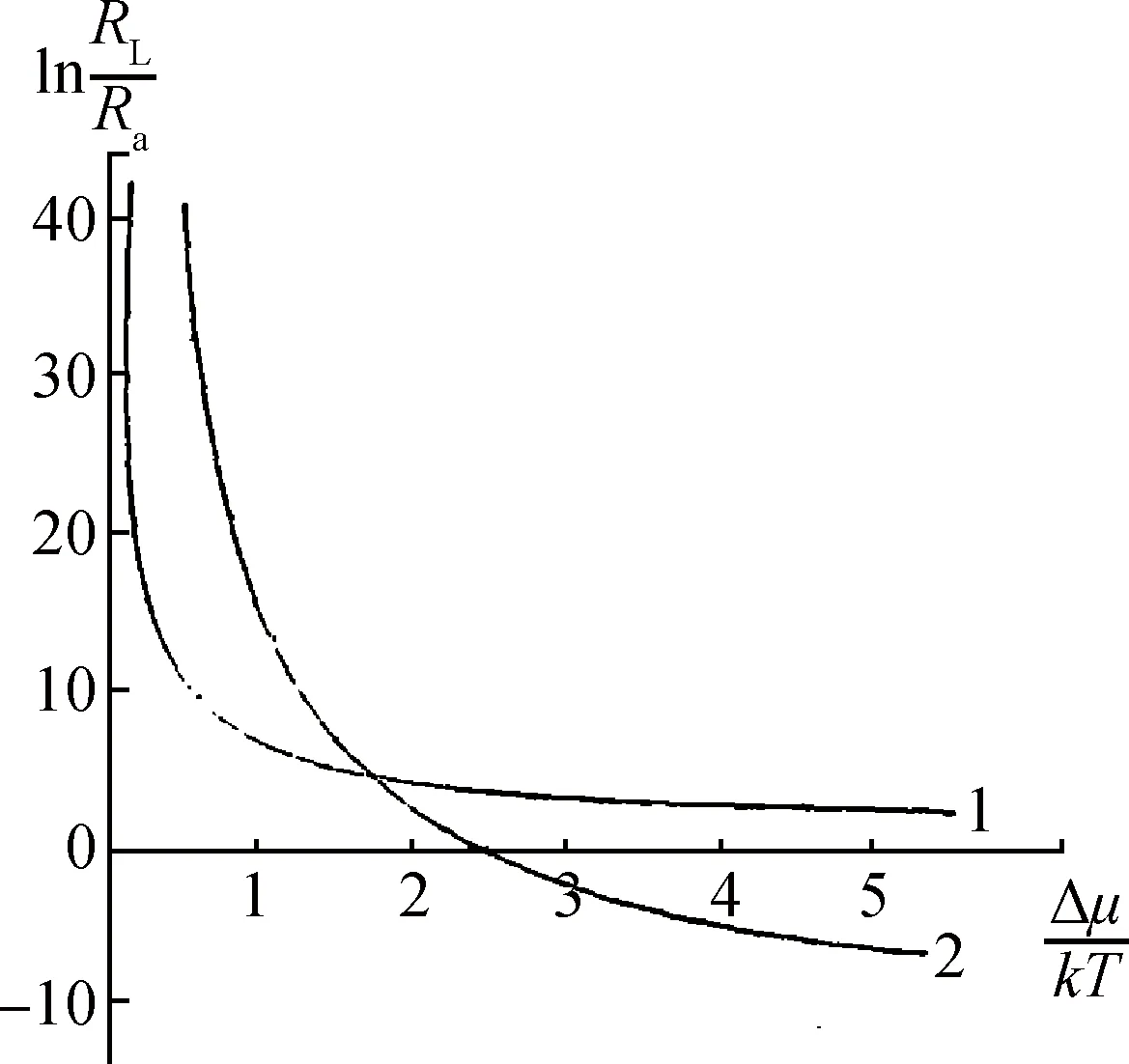
图5 ln(RL/Rs)与△μ/kT的关系。曲线1是多核层错机制的生长动力学与二维成核机制的对比;曲线2是单核层错机制与二维成核机制的对比Fig.5 The relationship of ln(RL/Rs) versus Δμ/KT for a comparison of stacking fault mechanism(SFM) with two dimensional nucleation mechanism. Curve 1 and curve 2 are for birth-and-spread model(SFM) and mono-nuclear model(SFM), respectirely
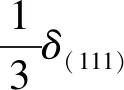
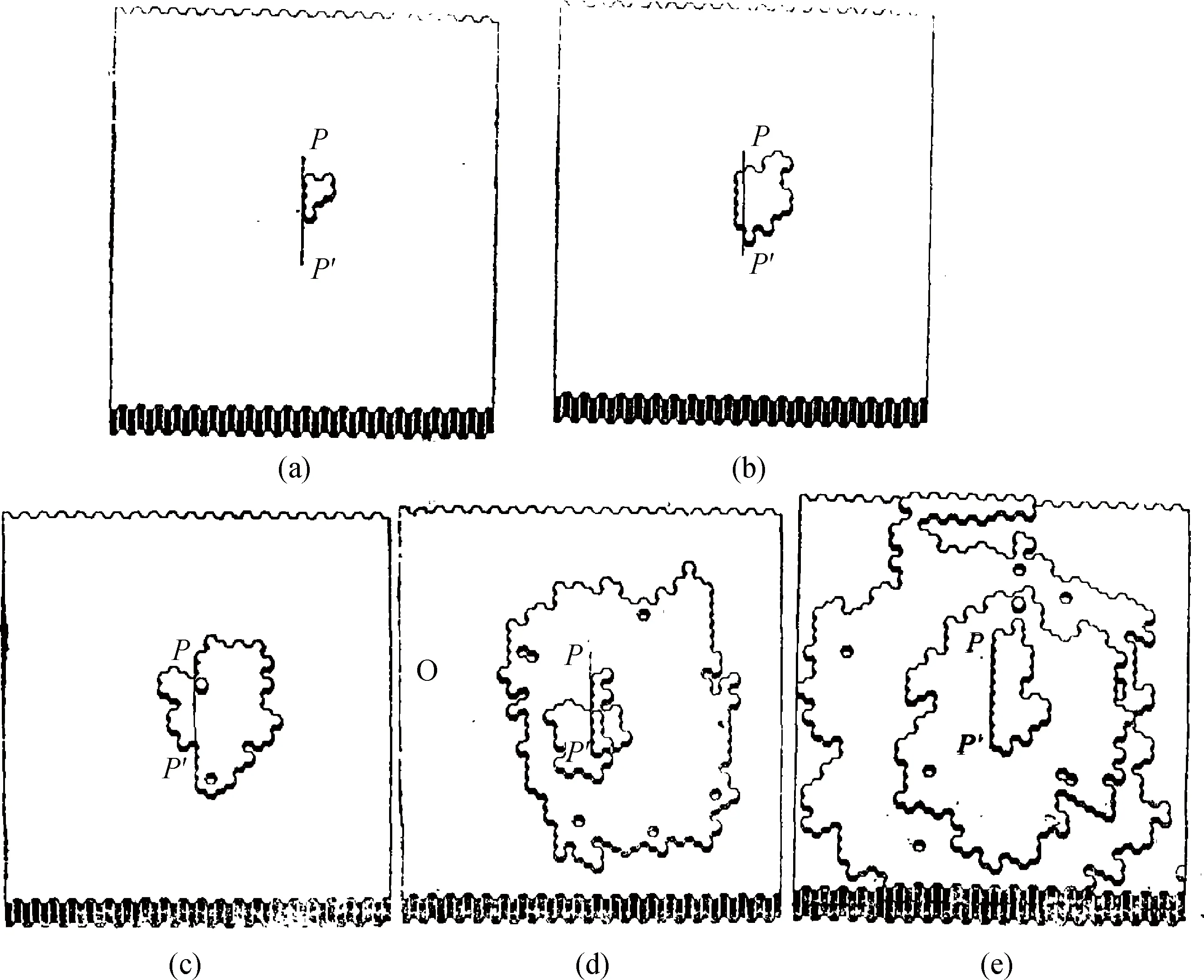
图6 在典型条件△μ/kT=4,φ/kT=4下,层错机制在面心立方晶体(111)面上的生长形貌,P和P′是层错边缘二不全位错的露头点,从(a)到(e)的模拟时间是107,2×107,3×107,5×107和108Fig.6 Surface growth morphology of stacking fault mechanism on (111) face of the fcc crystal for typical values of △μ/kT=4 and φ/kT=4.P and P′ are the emergente points on (111) surface of the two partial dislocations associated with the stacking fault. The simulation times for Fig.(a) to (e) are 107, 2×107, 3×107, 5×107 and 108,respectively
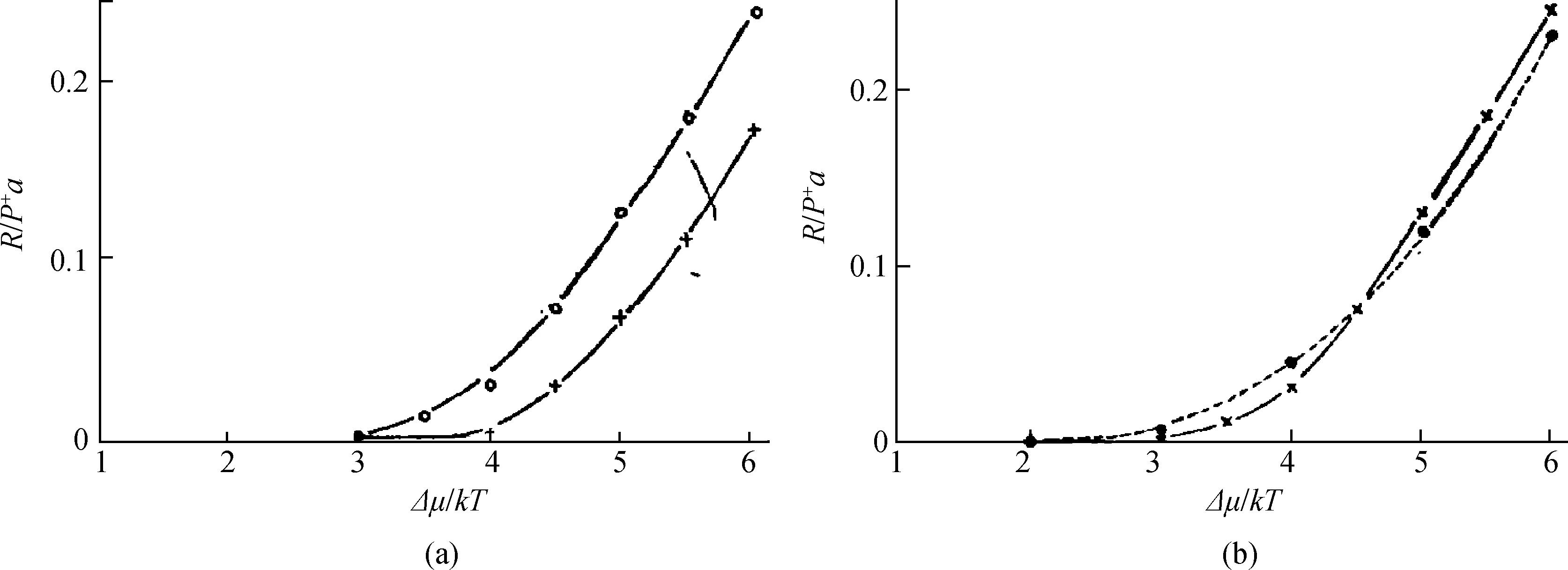
图7 在典型条件φ/kT=4下,无量纲生长速度与过饱和度△μ/kT的关系(a)层错机制与二维成核机制的对比,上面曲线为层错机制;(b)层错机制与螺位错机制的对比,实线为层错机制,虚线为螺位错机制Fig.7 The dimensionless growth rate R/P+a versus supersaturation △μ/kT for the typical value φ/kT=4(a)a comparison of kinetics between stacking fault mechanism(SFM) and two dimensional nucleation mechanism(2D-NM), the upper curve is for SFM and the lower one is for 2F-NM, (b)a comparison between screw dislocation mechanism(SDM) and SFM, the dash curve is for SDM and solid one is for SFM
4 晶体生长的孪晶机制
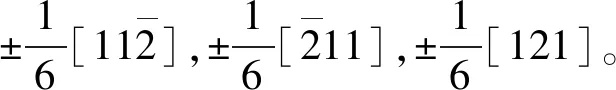
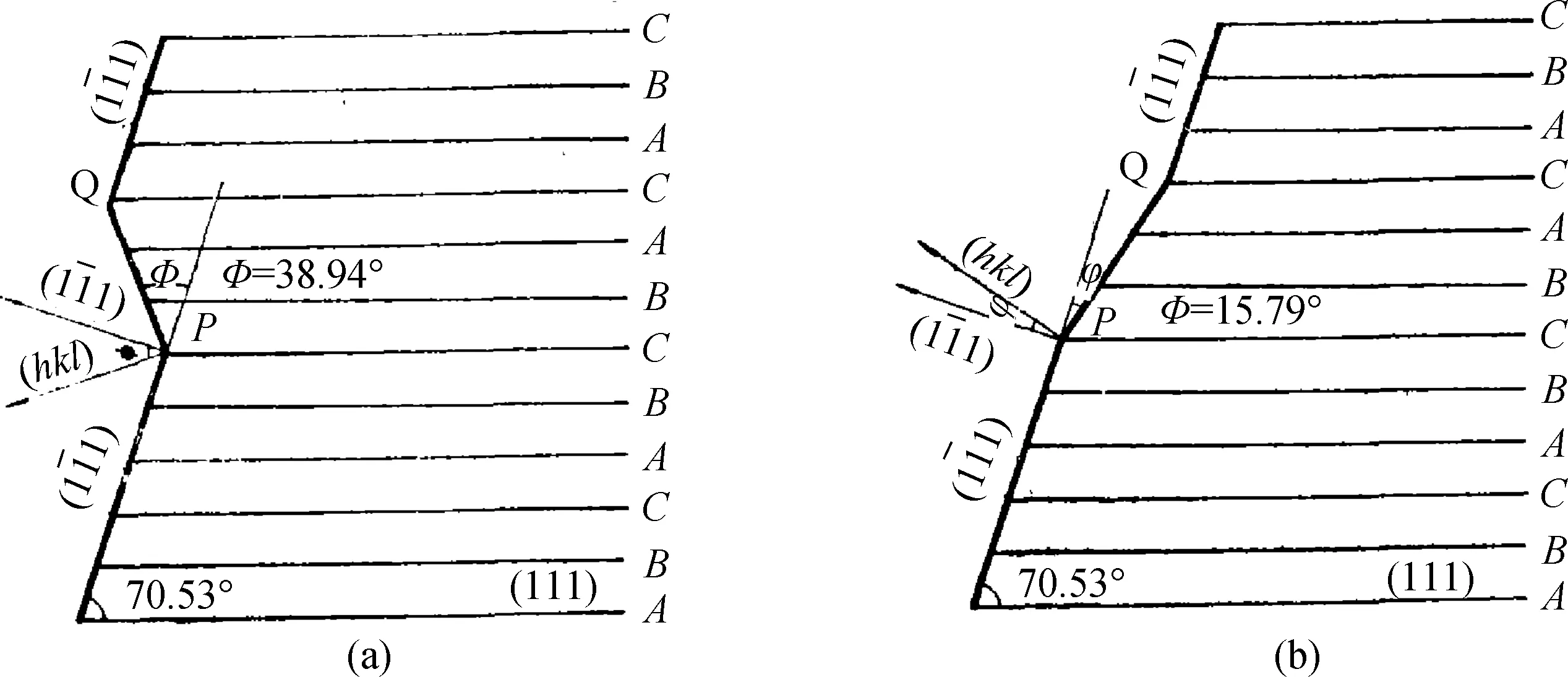
图8 由一系列相互平行层错所产生的两类孪晶,层错面为(111),生长表面为(11)由层错矢量产生的A类孪晶,面上孪生区在原坐标系中的面指数为在孪生坐标中的面指数为(111);(b)由层错矢量或产生的B类孪晶,孪生区在原坐标系中的面指数为在孪生坐标系中的面指数为Fig.8 Two kinds of twin lamellae resulting from a sequence of parallel stacking faults,the fault plane is (111), the growth surface is The twinned area on (11) in the twinned coordinate system;(b)B-type twinning with fault vector (1/6) in the un-twinned coordinate system and in the twinned coordinate system
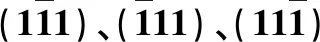
表2 面心立方晶体中一系列(111)层错导致的孪生晶在表面孪生区的面指数Table 2 Indices of swinned area on growth surface twinning is on (111) of fcc crystal
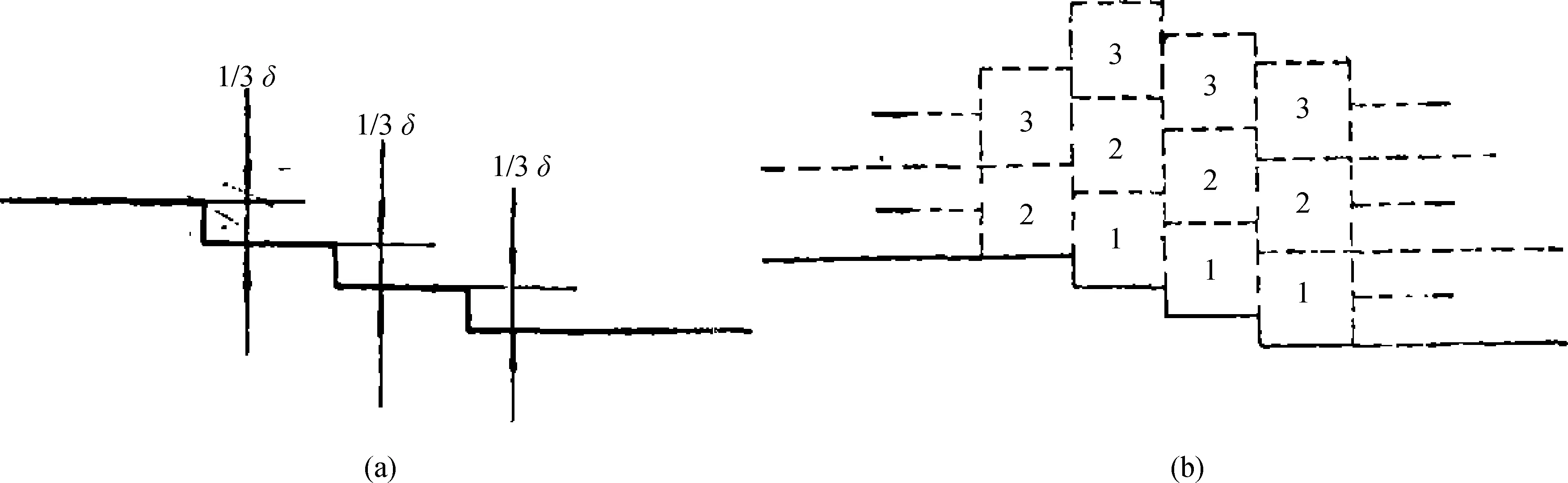
图9 产生台阶的孪晶机制; 孪晶为三片层错构成, 生长面为面心立方晶体的(111)面(a)层错与( 面相交处产生的三个高度为(1/3)δ(111)的亚台阶;(b)孪晶机制产生台阶的过程, 在孪晶两侧不断地产生全台阶Fig.9 Step generation mechanism of a twin lamella with three parallel stacking faults on fcc (111) surface(a)Three sub-steps with height of (1/3) δ(111)(δ(111) is the thickness of an elementary growth layer on (111) surface).(b)The operation of the twin lamella mechanism for step generation; two full steps are created continually at both sides of twin lamella at the same time
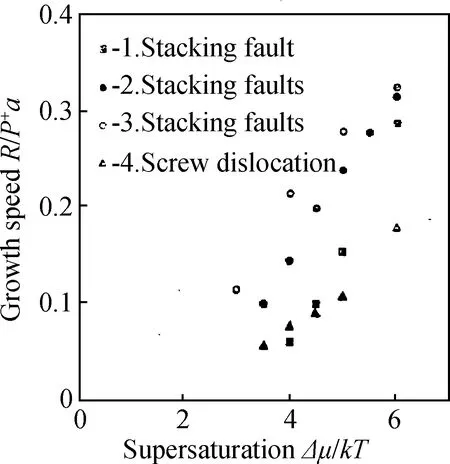
图10 在典型条件下(φ/kT=4.0),面心立方晶体(111)面不同生长机制的无量纲生长速率R/P+a与饱和度△μ/kT之关系Fig.10 Dimensionless growth rate R/P+a of an fcc(111) surface versus supersaturatlon for the typieal value of φ/kT=4.0 on which emerged the stacking fault,the twin lamellae with different number of stacking faults and the couple of screw dislocations. P+ is the impingement rate and a is the lattice parameter
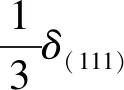

表3 在过饱和度△μ/kT=6时面心立方晶体(100) 完整表面的生长速率与具有孪晶头区的(111)面生长速率的对比;该孪晶由不同片数的层错构成Table 3 Growth rate of (100) perfect surface and (111) surface on whieh emerged the outcrop of a twin lamella composed of different number of stacking faults at △μ/kT=6.0
5 重入角生长和粗糙面生长的协同机制
在晶体可沿任何方向生长的各向同性生长系统中,我们考虑一面心立方的五个{111}面构成的多面体,该多面体的上半部经B型孪生操作,因而多面体的三个侧面的上部其原子组态为{100}面,下部仍保持{111}面的原子组态,而其顶面和底面都是{111},如图11(a)所示。先考虑一个极限情况,即在生长系统中的过饱和度足够小以致{111}面不能通过二维成核机制生长,但过饱和度又足够大以保证粗糙面{100}能够生长。这种假定是合理的,因为面心立方晶体的{111}面是“光滑面”,只有超过二维成核的临界过饱和度时才能生长,而{100}面是粗糙面[21-24],不存在二维成核位垒,在任何过饱和度下都能生长。在这种条件下,三个侧面的{111}部分和顶面和底面都不能生长,只有三个侧面的(100)部分能够生长。由于晶面淘汰律,生长的结果造成{100}面在多面体上消失,又由于孪晶的存在,出现了三个70.53°的重入角,如图11(b)所示。已经得到证明,在70.53°重入角上的任何原子坐位相当于生长过程中最为活跃的扭折(kink)坐位[11],于是重入角生长机制启动,重入角机制的生长结果是重入角消失和粗糙面{100}呈现,见图11(c)。粗糙面机制再度生长,其结果是粗糙面消失,同时109.47°的重入角出现,见图11(d)。109.47°的重入角相当于永不消失的全台阶[11],在生长过程中仍极活跃,于是重入角机制又开始工作。这样重入角机制与粗糙面机制交替工作,结果长成板块状晶体。这可用来解释天然矿物晶体中大量板块晶体的形成[11]。
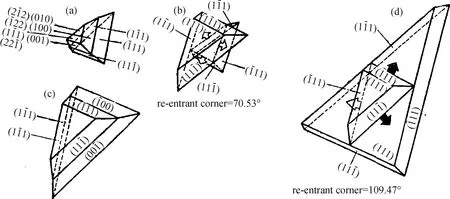
图11 粗糙面生长与重入角(re-entrant corner)生长的协同机制Fig.11 Schematical illustration of an alternative cooperation of rough surface and re-entrant corner growth mechanism. A plate-like crystal is formed by this mechanism
在通常所遇到的生长条件下,粗糙度较大的{100}面的生长速度总是比光滑面{111}的速度大,上述机制仍能工作,不过不是交替工作,而是协同工作,也就是说在同一时刻两种机制相互协同、同时工作。其结果仍然是长出板块晶体。
6 结 论
基于缺陷引起的点阵畸变以及缺陷邻近原子组态的分析,对实际晶体生长过程中的缺陷机制进行了系统的描述。已经证明,除螺位错外,任何类型的位错、层错、孪晶都能成为永不消失的台阶源。因此实际晶体的生长比迄今人们所理解的螺位错是唯一的台阶源要容易很多。

