初中数学教学中数形结合教学模式的应用探究

摘 要：当前教育在注重知识传授的同时，对学生学科思想意识的培养也越来越重视。数形结合是数学领域常用的一种思想，对解题、训练思维、培养数学意识都有重大意义。文章重点阐述了数形结合在初中数学教学中的应用。

关键词：数形结合;初中数学;函数

中图分类号：G633.6     文章编号：2095-624X（2019）18-0083-01

一、数形结合思想在初中数学中的应用

1.应用于数与代数

以形助数是数形结合思想的重要体现，应用于初中数学，对锻炼学生思维、提高解题效率大有帮助。如题目1：代数式√x2+4+√（12-x）2+9的最小值是多少？我们可通过构造图形来解这道题目，首先作一线段AB=12，在AB上取点C，假设AC=x，则BC=12-x，然后作AD⊥AB，BE⊥AB，且使AD等于2，BE=3，再依次连接CD、CE、DE。解题思路是把代数和勾股定理相联系，即CD=√x2+4，CE=√（12-x）2+9。若C、D、E三点不在同一条直线上，则构成△CDE;而CD+CE的最小值应当是三点位于同一直线，所以CD+DE=DE时为最小值，即√（AD+BE）2+122=13。

2.应用于解方程（组）

二元一次方程组和一元二次方程都是初中数学的重点，解方程的方法很多。除了从单纯的数的层面解答，还可以考虑运用图像，尤其是在解答一些较为复杂的方程时，不妨尝试两种方法结合使用，会使解题效率大幅提升。

相对而言，一元二次方程的难度要高于二元一次方程组，除了配方法、因式分解、求根公式等，同样可以用图形来解题。比如，运用图像观察法解一元二次方程 —x2-—x-1=0。根据所给方程正确画出相应的二次函数图，然后可以直观地看到函数与x轴有两个交点，分别为（-1，0）、（2，0），即原方程有两个实根，-1和2。

3.应用于函数

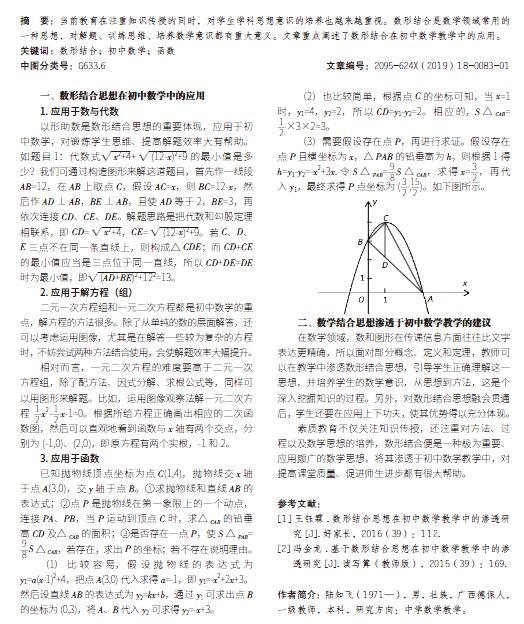
已知抛物线顶点坐标为点C（1，4），抛物线交x轴于点A（3，0），交y轴于点B。①求抛物线和直线AB的表达式;②点P是抛物线在第一象限上的一个动点，连接PA、PB，当P运动到顶点C时，求△CAB的铅垂高CD及△CAB的面积;③是否存在一点P，使S△PAB=   —S△CAB，若存在，求出P的坐标;若不存在说明理由。

（1）比较容易，假设抛物线的表达式为y1=a（x-1）2+4，把点A（3，0）代入求得a=-1，即y1=-x2+2x+3。然后设直线AB的表达式为y2=kx+b，通过y1可求出点B的坐标为（0，3），将A、B代入y2可求得y2=-x+3。

（2）也比较简单，根据点C的坐标可知，当x=1时，y1=4，y2=2，所以CD=y1-y2=2。相应的，S△CAB= —×3×2=3。

（3）需要假设存在点P，再进行求证。假设存在点P且横坐标为x，△PAB的铅垂高为h，则根据1得h=y1-y2=-x2+3x.令S△PAB=—S△CAB，求得x=—，再代入y1，最终求得P点坐标为（—，—）。如下图所示。

二、数学结合思想渗透于初中数学教学的建议

在数学领域，数和图形在传递信息方面往往比文字表达更精确，所以面对部分概念、定义和定理，教师可以在教学中渗透数形结合思想，引导学生正确理解这一思想，并培养学生的数学意识，从思想到方法，这是个深入挖掘知识的过程。另外，对数形结合思想融会贯通后，学生还要在应用上下功夫，使其优势得以充分体现。

素質教育不仅关注知识传授，还注重对方法、过程以及数学思想的培养，数形结合便是一种极为重要、应用颇广的数学思想，将其渗透于初中数学教学中，对提高课堂质量、促进师生进步都有很大帮助。

参考文献：

[1]王钰霖.数形结合思想在初中数学教学中的渗透研究[J].好家长，2016（39）：112.

[2]冯金龙.基于数形结合思想在初中数学教学中的渗透研究[J].读写算（教师版），2015（39）：169.

作者简介：陆知飞（1971—），男，壮族，广西德保人，一级教师，本科，研究方向：中学数学教学。