小议数形结合方法在初中数学教学中的应用

徐利

【摘要】初中阶段，是学生各种思维模式逐渐养成的阶段，尤其是数学思维.数形结合方法是学生培养数学思維的重要方法，教师要更加注重教学中这种方法的应用，帮助学生建立空间思维模式.本文从初中数学教学中的实际应用出发对数形结合问题进行探讨，进而提出相关应用策略.

【关键词】数形结合方法;初中数学教学;应用

同语文等学科不同，数学学习需要较强的逻辑性，这也是很多学生在学习数学时感到比较吃力的重要原因.因此，教师在教学过程中要结合实际，设计行之有效的教学方法，注重培养学生的数学思维能力.数形结合的方法已经被很多教育工作者所使用，这种方法具有高效性和准确性的特点，为教师教学质量的提高提供保障.

一、数形结合方法在初中数学教学中的应用

（一）在几何问题中的应用

数形结合主要是指将“数”与“形”进行结合，使原本抽象的知识变得具体而直观，从而达到化繁为简的目的，为解决实际问题奠定基础.对初中生来说，几何问题一直都是他们理解的难点，这一部分知识较为抽象，如果没有一个良好的数学思维很难快速地解题.而利用数形结合的方法，将原本的图形数字化，这样学生能够用平时的数学思维进行解答，大大提高了解题效率.

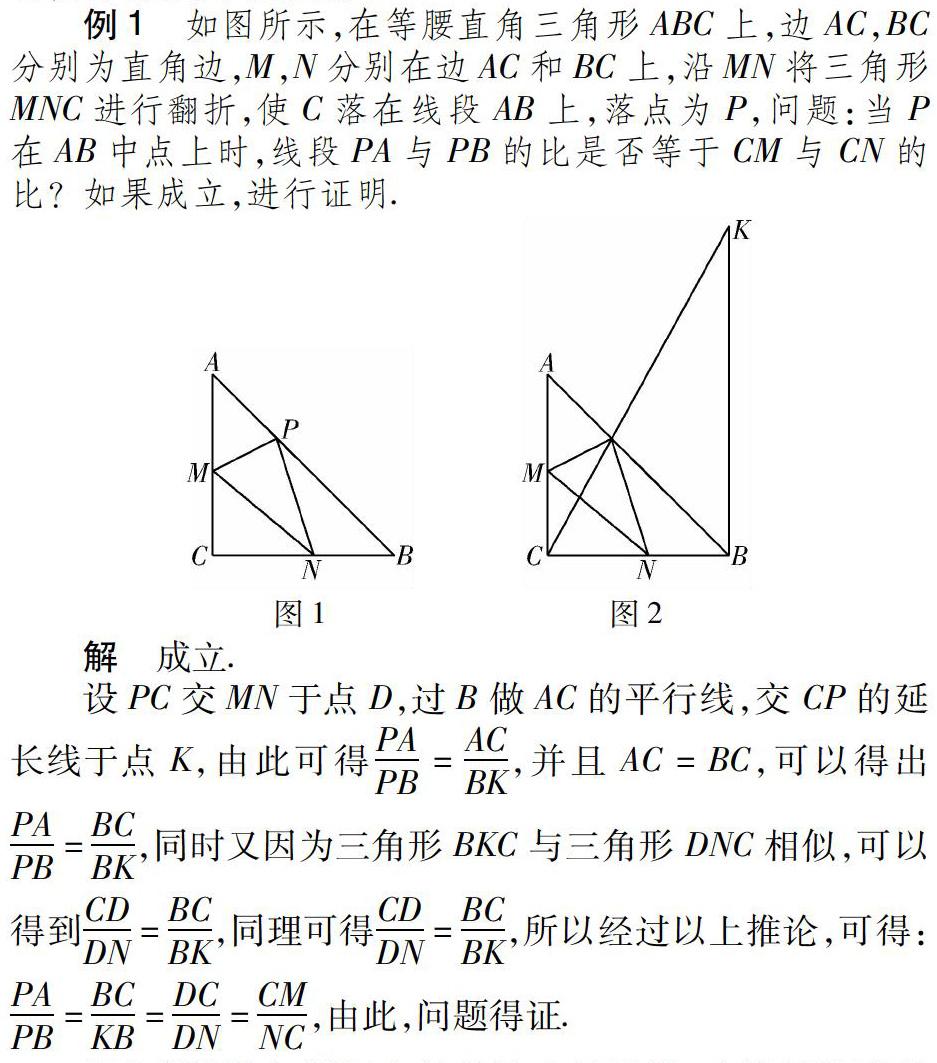
例1 如图所示，在等腰直角三角形ABC上，边AC，BC分别为直角边，M，N分别在边AC和BC上，沿MN将三角形MNC进行翻折，使C落在线段AB上，落点为P，问题：当P在AB中点上时，线段PA与PB的比是否等于CM与CN的比？如果成立，进行证明.

解 成立.

设PC交MN于点D，过B做AC的平行线，交CP的延长线于点K，由此可得PAPB=ACBK，并且AC=BC，可以得出PAPB=BCBK，同时又因为三角形BKC与三角形DNC相似，可以得到CDDN=BCBK，同理可得CDDN=BCBK，所以经过以上推论，可得：PAPB=BCKB=DCDN=CMNC，由此，问题得证.

以上例题的解题根本就是构造辅助线，这就是数形结合的一种思维，在辅助线的引导下，解题会更加顺畅.

（二）在函数问题中的应用

函数问题，一直以来都是初中数学教学的重点内容，其中二次函数问题最为重要.因此，在解答二次函数问题时，依据数形结合的思维，会给解题带来更大的方便，对学生加深理解、提高解题速度起到重要作用.[1].

在解答二次函数与一元二次方程时可以这样解答：因为一元二次方程ax2+bx+c=0可以看成是二次函数y=ax2+bx+c，y=0时的特殊情况，这时就可以利用二次函数图像与x轴的交点情况进行解答.可以分为三种情况进行解答，即方程有两个根时，函数图像与x轴两个交点;方程一个根时，函数图像与x轴一个交点;没有根时，函数与x轴没有交点.

（三）在概率问题中的应用

初中数学新课程标准要求，教师在教学过程中要加强学生对概率和统计知识的学习.在进行统计分析过程中可以锻炼学生提出问题、分析问题和解决问题的能力，无论是对学生的成长发展，还是对教师教学质量的提高都产生重要作用.其中概率问题中树形图的运用就较好地体现了数形结合的思想，比如，以下例题：

在甲乙两地之间有M和N两条道路，小敏从甲到N，小刚从乙到甲，两个人一起出发，如果每个人从两条路中间都任意选择一条，求他们相遇的概率.这道题是典型的概率问题，如果不借助图形的辅助，光是看题目，很难得到有用的信息，时间久了，学生就会产生厌烦，不利于学习兴趣的培养.而采用数形结合的方式，画出树形图，学生更直观地考虑问题，答案也自然的很容易得出了.其中等可能的结果有四种，分别是AA，AB，BB，BA，其中两人相遇有两种，为AA，BB，所以两人相遇的概率为12.

二、数形结合方法在初中数学教学中应用的对策分析

（一）借助多媒体手段

通过接触网络，我们了解到，网络可以把相对具体的东西通过视频、图像、音频等手段表现出来，而现在很多学校也都在开展微课程教育，将多媒体应用引入课堂教学之中.数形结合教育是将抽象的事物具体化、模型化和数字化，依据这一特点，教师在数学课堂上完全可以将数形结合教育与多媒体教育相结合，通过动态的演示，将二维视图转化为三维视图，不但有利于学生进行理解，还能更好地培养学生的空间感，对提高学生数学思维能力发挥重要作用.

（二）培养学生空间思维能力

数形结合方法的运用需要学生具有较强的空间思维能力，只有在脑海中存在很强的空间感，学生在解题时才能将具体的题目通过思考画出图形.所以，教师在进行教学时要加强引导，在平时授课中也要培养学生的空间思维意识，尤其是一些几何问题，如果不具备立体思维，很难将图形画出来，以长方体为例，如果题目问到如果有一个蓄水池，长、宽、高分别为6米、7米、8米，为蓄水池墙面铺塑料布，求所需塑料布的面积.在解答这道题时，学生往往根据固定的思维，根据长方体表面积公式很快地就将题解出来了，但是并不正确，因为要根据实际情况，用总的表面积减去上下两个面的面积，才能得出正确的答案.

三、结 语

数形结合方法已经在教学领域得到了广泛应用，只有认识到数不离形，形不离数，将两者紧密结合起来才能更好地运用这一方法.同时，在进行应用时还要做到灵活性，必要时要做到数与形的转化.教师要充分认识到数形结合方法的重要性，从而在教学中帮助学生锻炼思维能力，提高学习兴趣.

【参考文献】

[1]朱家宏.初中数学教学中数形结合思想的应用[J].科技视界，2015（9）：175-206.